第4章 平行四边形单元检测卷(含答案)
文档属性
| 名称 | 第4章 平行四边形单元检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1005.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
平行四边形单元检测卷(含答案)
一、选择题
1.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线是中心对称图形的是( )
A. B. C. D.
2.如图,在平行四边形中,的平分线交于点,的平分线交于点,若,则的长是( )
A.2 B.4 C.5 D.6
3.如图,在中,,将点C沿折叠至点E,连接,当从变化过程中,四边形恰为平行四边形时,此时四边形的周长是( )
A. B.16 C.14 D.
4.如图,在中,以A为圆心,长为半径画弧交于F,连接;再分别以B,F为圆心,大于长为半径画弧,两弧交于点G,连接并延长交于E.则以下结论:①平分;②平分;③垂直平分线段;④.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
5.如图,在正方形网格中,A,B,C,D,E,F,G,H,I,J是网格线交点,与关于某点成中心对称,则其对称中心是( )
A.点G B.点H C.点I D.点J
6.在 ABCD中,∠ABC=30°,AB=8,AC=5,则 ABCD的周长是( )
A.或 B.或
C.或 D.或
7.如图所示,点为 内一点,连接,,,,,已知的面积为,的面积为,则阴影部分的面积为( )
A.6 B.8 C.10 D.12
8.如图,平行四边形ABCD中,O为对角线交点, DP平分∠ADC,CP 平分∠BCD,AB=7, AD=10, 则 OP的长为( ) .
A.1.5 B.2 C.2.5 D.3
9.如图,在四边形中,,,,,点为上异于、的一定点,点为上的一动点,、分别为、的中点,当从到的运动过程中,线段扫过图形的面积为( )
A.4 B.4.5 C.5 D.6
10.如图,在四边形纸片ABCD中,∠A+∠B=150°,将纸片折叠,使点C、D落在边AB上的点C'、D'处,折痕为MN,则∠AMD'+BNC'=( )
A.50° B.60° C.70° D.80°
二、填空题
11.已知一个多边形的每个外角都为,则这个多边形的边数是
12.如图,在等腰中,,,点是边上一点,且,连结,过点作的角平分线交于点.若点是边的中点,连结,则的长为 .
13.如图,E是平行四边形ABCD内一点,△BCE是正三角形,连结AE,DE,若AELAD,DE⊥EC,且AE=1,∠ADE=30",则AB的长是 .
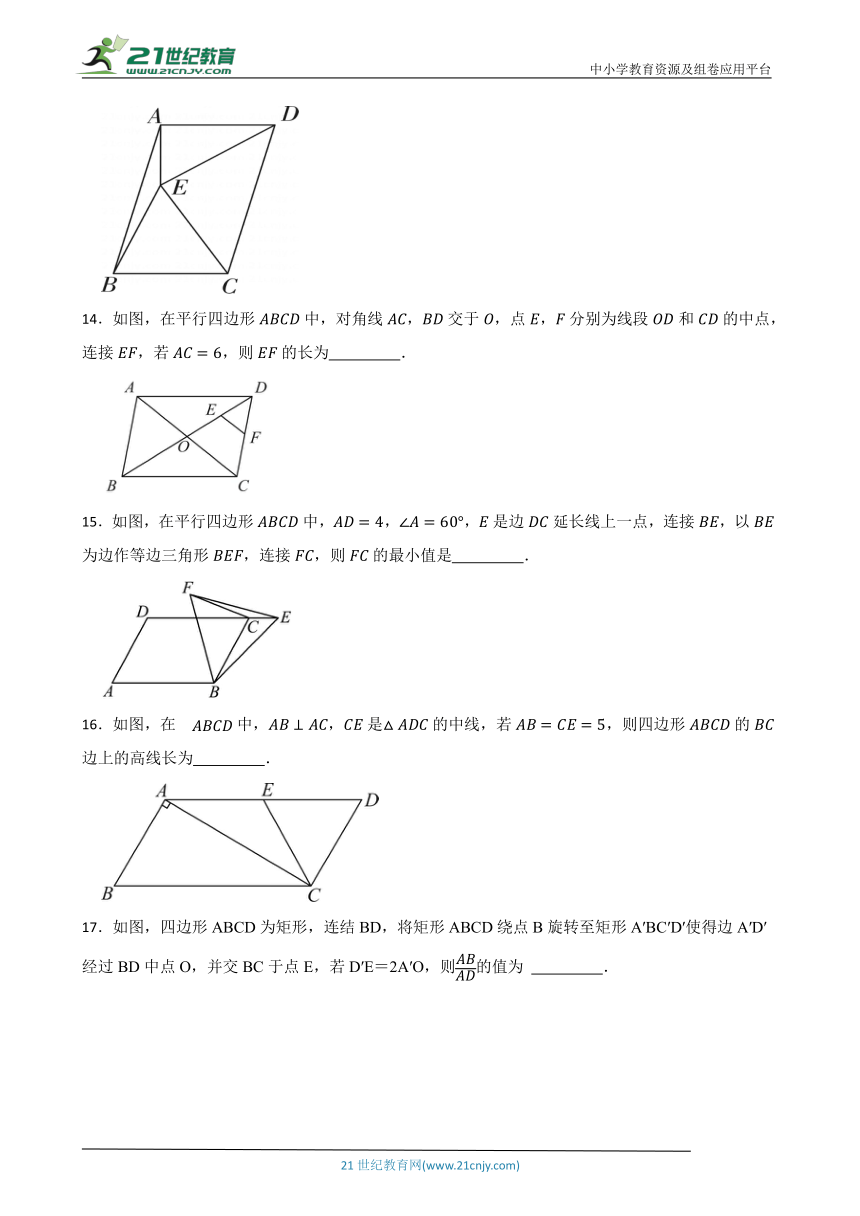
14.如图,在平行四边形中,对角线,交于,点,分别为线段和的中点,连接,若,则的长为 .
15.如图,在平行四边形中,,,是边延长线上一点,连接,以为边作等边三角形,连接,则的最小值是 .
16.如图,在中,,是的中线,若,则四边形的边上的高线长为 .
17.如图,四边形ABCD为矩形,连结BD,将矩形ABCD绕点B旋转至矩形A′BC′D′使得边A′D′经过BD中点O,并交BC于点E,若D′E=2A′O,则的值为 .
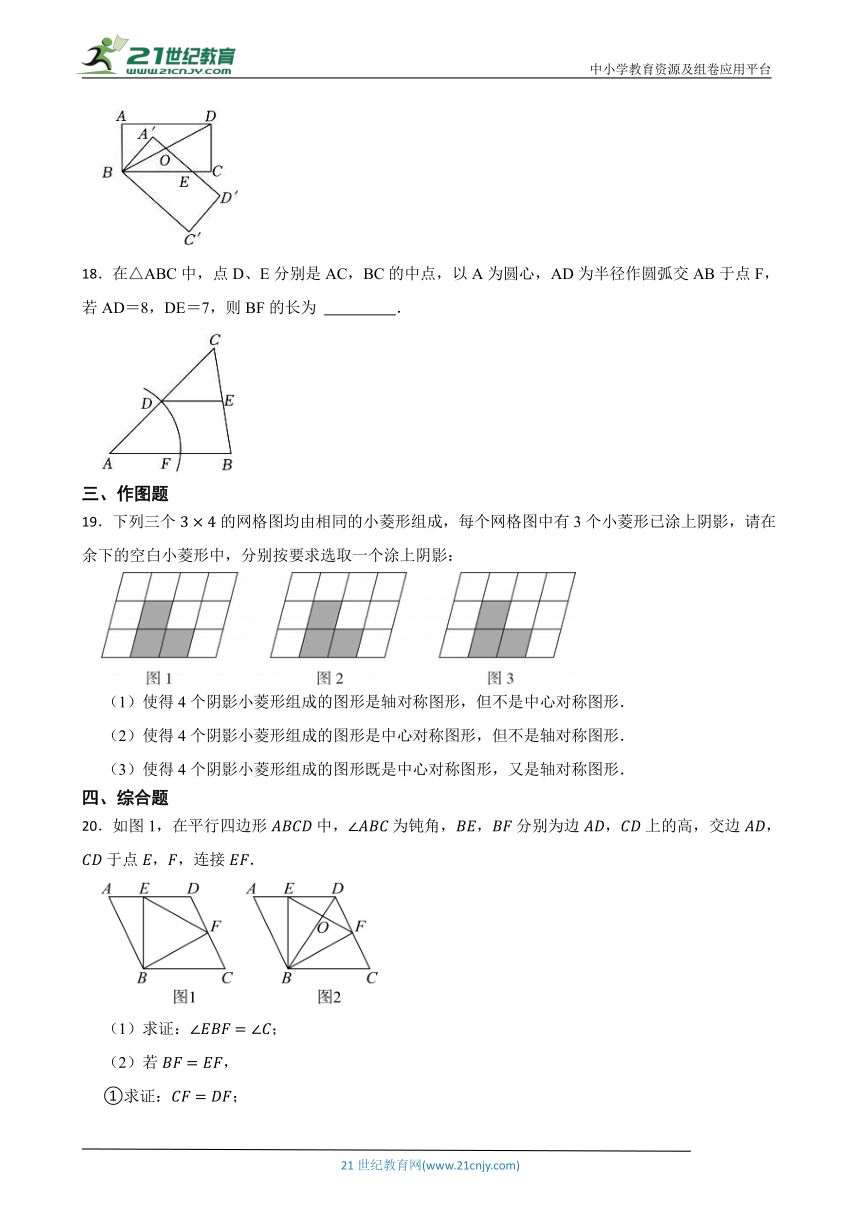
18.在△ABC中,点D、E分别是AC,BC的中点,以A为圆心,AD为半径作圆弧交AB于点F,若AD=8,DE=7,则BF的长为 .
三、作图题
19.下列三个的网格图均由相同的小菱形组成,每个网格图中有3个小菱形已涂上阴影,请在余下的空白小菱形中,分别按要求选取一个涂上阴影:
(1)使得4个阴影小菱形组成的图形是轴对称图形,但不是中心对称图形.
(2)使得4个阴影小菱形组成的图形是中心对称图形,但不是轴对称图形.
(3)使得4个阴影小菱形组成的图形既是中心对称图形,又是轴对称图形.
四、综合题
20.如图1,在平行四边形中,为钝角,,分别为边,上的高,交边,于点,,连接.
(1)求证:;
(2)若,
①求证:;
②如图2,连接交于点,若,的面积为4,求与的面积之差.
21.如图1,在中,中线BE,CF交于点O,G,H分别是OB,OC的中点,连结EF,FG,GH,HE.
(1)求证:四边形EFGH是平行四边形;
(2)如图2,连接OA,若,求四边形BCEF面积和OA的长.
22.如图1,在平行四边形ABCD中,点E、F分别为AD,BC的中点,点G,H在对角线BD上,且BG=DH.
(1)求证:四边形EHFG是平行四边形.
(2)如图2,连结AC交BD于点O,若AC⊥EH,OH=BH,OH=2,求AB的长.
23.如图,点O是坐标原点,四边形是平行四边形,点A的坐标为,点B的坐标为.动点P从O出发,沿射线方向以每秒2个单位的速度运动,点Q从B出发以每秒1个单位的速度向点C运动,它们同时出发,当点Q到达点C时P点也停止运动.设运动时间为t秒.
(1)写出点C的坐标为 ;
(2)求当t为何值时,以P,Q,A,B为顶点的四边形是平行四边形;
(3)在点P,Q运动过程中,连接,
①当t为何值时,使垂直于平行四边形的某一边.
②若点C关于的对称点恰好落在x轴上,则点Q的坐标为 ▲ .
24.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连结AC,BD,CD,得ABDC.
(1)求ABDC的面积;
(2)若在x轴上存在点M,连结MA,MC,使S△MAC=S平行四边形ABDC,求出点M的坐标;
(3)若点P从点D开始以每秒个单位的速度向终点C运动,同时点Q从点A开始以每秒个单位的速度向终点B运动,当一个到达终点时,另一个也停止运动.问运动几秒时,以A,P,C,Q为顶点的四边形是平行四边形?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】A
9.【答案】A
10.【答案】B
11.【答案】6
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】6
19.【答案】(1)解:
(2)解:
(3)解:
20.【答案】(1)证明:四边形是平行四边形,,分别为边,上的高,
,
,
,
;
(2)解:①证明:在上取一点,使得,连接,
,
,
,
,
,
,
,
在和中,
,
,
,,
,
,
,
;
②四边形是平行四边形,,分别为边,上的高,
,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
,
,
,即,
解得:,,
,
,
,,
.
21.【答案】(1)证明:分别是AC,AB的中点,
;
分别是OB,OC的中点,
;
四边形EFGH是平行四边形.
(2)解:在中,
是菱形,
,
分别是AB,OB的中点,
.
22.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠EDH=∠FBG,
∵E、F分别为AD,BC的中点,
∴DE=AE=AD,BF=CF=BC,
∴DE=BF,
在△DHE和△BGF中,
,
∴△DHE≌△BGF(SAS),
∴EH=FG,∠EHD=∠FGB,
∴EH∥FG,
∴四边形EHFG是平行四边形.
(2)解:如图②,设AC交EH于点L,连接OF,
∵OH=BH,CF=BF,
∴FH∥AC,
∵AC⊥EH,
∴∠FHE=∠ALH=90°,
∴四边形EHFG是矩形,
∴∠GFH=90°,
∵OG=OH=2,
∴OF=OG=GH=2,
∵CO=AO,CF=BF,
∴AB=2OF=2×2=4,
∴AB的长是4.
23.【答案】(1)
(2)解:当点P在线段上时,如图2,∵,
∴,
由题意可知:,,
又∵,
∴,
当四边形为平行四边形,则有,即,
解得;
当点P在线段的延长线上时,如图3,同上可知:,,,
∴,
∵四边形为平行四边形,
∴,即,
解得,即点Q与点C重合,
综上可知,当或14时,以P,Q,A,B为顶点的四边形是平行四边形;
(3)解:①当,如图1由(1)可知,延长交y轴于点D,
∵四边形是平行四边形,
∴,
∵轴,
∴轴,
∴,
∴四边形是矩形,
∴,,
∴,即;
当时,如图4由(1)可知,,则,,
∴,即,
过点Q作于点F,过点Q作于点E,延长交y轴于点D,
∵,
∴四边形是矩形,
∴,,
∵,,
∴四边形是平行四边形,
∴,,
∴,,
∵,,
∴,
∴,
又∵,
∴,
∴,即,
∴,解得,
综上所述,当或10时,使垂直于平行四边形的某一边;
②
24.【答案】(1)解:由题意可得:AB=4,OC=2,
ABDC的面积为8.
(2)解:∵S△MAC= S平行四边形ABDC=8,OC=2,
∴AM=8,
∴M(-9,0)或(7,0)
(3)解:要使以A,P,C,Q为顶点的四边形是平行四边形,则需CP=AQ,
即4- t= t.
∴t= 秒.
21世纪教育网(www.21cnjy.com)
平行四边形单元检测卷(含答案)
一、选择题
1.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线是中心对称图形的是( )
A. B. C. D.
2.如图,在平行四边形中,的平分线交于点,的平分线交于点,若,则的长是( )
A.2 B.4 C.5 D.6
3.如图,在中,,将点C沿折叠至点E,连接,当从变化过程中,四边形恰为平行四边形时,此时四边形的周长是( )
A. B.16 C.14 D.
4.如图,在中,以A为圆心,长为半径画弧交于F,连接;再分别以B,F为圆心,大于长为半径画弧,两弧交于点G,连接并延长交于E.则以下结论:①平分;②平分;③垂直平分线段;④.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
5.如图,在正方形网格中,A,B,C,D,E,F,G,H,I,J是网格线交点,与关于某点成中心对称,则其对称中心是( )
A.点G B.点H C.点I D.点J
6.在 ABCD中,∠ABC=30°,AB=8,AC=5,则 ABCD的周长是( )
A.或 B.或
C.或 D.或
7.如图所示,点为 内一点,连接,,,,,已知的面积为,的面积为,则阴影部分的面积为( )
A.6 B.8 C.10 D.12
8.如图,平行四边形ABCD中,O为对角线交点, DP平分∠ADC,CP 平分∠BCD,AB=7, AD=10, 则 OP的长为( ) .
A.1.5 B.2 C.2.5 D.3
9.如图,在四边形中,,,,,点为上异于、的一定点,点为上的一动点,、分别为、的中点,当从到的运动过程中,线段扫过图形的面积为( )
A.4 B.4.5 C.5 D.6
10.如图,在四边形纸片ABCD中,∠A+∠B=150°,将纸片折叠,使点C、D落在边AB上的点C'、D'处,折痕为MN,则∠AMD'+BNC'=( )
A.50° B.60° C.70° D.80°
二、填空题
11.已知一个多边形的每个外角都为,则这个多边形的边数是
12.如图,在等腰中,,,点是边上一点,且,连结,过点作的角平分线交于点.若点是边的中点,连结,则的长为 .
13.如图,E是平行四边形ABCD内一点,△BCE是正三角形,连结AE,DE,若AELAD,DE⊥EC,且AE=1,∠ADE=30",则AB的长是 .
14.如图,在平行四边形中,对角线,交于,点,分别为线段和的中点,连接,若,则的长为 .
15.如图,在平行四边形中,,,是边延长线上一点,连接,以为边作等边三角形,连接,则的最小值是 .
16.如图,在中,,是的中线,若,则四边形的边上的高线长为 .
17.如图,四边形ABCD为矩形,连结BD,将矩形ABCD绕点B旋转至矩形A′BC′D′使得边A′D′经过BD中点O,并交BC于点E,若D′E=2A′O,则的值为 .
18.在△ABC中,点D、E分别是AC,BC的中点,以A为圆心,AD为半径作圆弧交AB于点F,若AD=8,DE=7,则BF的长为 .
三、作图题
19.下列三个的网格图均由相同的小菱形组成,每个网格图中有3个小菱形已涂上阴影,请在余下的空白小菱形中,分别按要求选取一个涂上阴影:
(1)使得4个阴影小菱形组成的图形是轴对称图形,但不是中心对称图形.
(2)使得4个阴影小菱形组成的图形是中心对称图形,但不是轴对称图形.
(3)使得4个阴影小菱形组成的图形既是中心对称图形,又是轴对称图形.
四、综合题
20.如图1,在平行四边形中,为钝角,,分别为边,上的高,交边,于点,,连接.
(1)求证:;
(2)若,
①求证:;
②如图2,连接交于点,若,的面积为4,求与的面积之差.
21.如图1,在中,中线BE,CF交于点O,G,H分别是OB,OC的中点,连结EF,FG,GH,HE.
(1)求证:四边形EFGH是平行四边形;
(2)如图2,连接OA,若,求四边形BCEF面积和OA的长.
22.如图1,在平行四边形ABCD中,点E、F分别为AD,BC的中点,点G,H在对角线BD上,且BG=DH.
(1)求证:四边形EHFG是平行四边形.
(2)如图2,连结AC交BD于点O,若AC⊥EH,OH=BH,OH=2,求AB的长.
23.如图,点O是坐标原点,四边形是平行四边形,点A的坐标为,点B的坐标为.动点P从O出发,沿射线方向以每秒2个单位的速度运动,点Q从B出发以每秒1个单位的速度向点C运动,它们同时出发,当点Q到达点C时P点也停止运动.设运动时间为t秒.
(1)写出点C的坐标为 ;
(2)求当t为何值时,以P,Q,A,B为顶点的四边形是平行四边形;
(3)在点P,Q运动过程中,连接,
①当t为何值时,使垂直于平行四边形的某一边.
②若点C关于的对称点恰好落在x轴上,则点Q的坐标为 ▲ .
24.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连结AC,BD,CD,得ABDC.
(1)求ABDC的面积;
(2)若在x轴上存在点M,连结MA,MC,使S△MAC=S平行四边形ABDC,求出点M的坐标;
(3)若点P从点D开始以每秒个单位的速度向终点C运动,同时点Q从点A开始以每秒个单位的速度向终点B运动,当一个到达终点时,另一个也停止运动.问运动几秒时,以A,P,C,Q为顶点的四边形是平行四边形?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】A
9.【答案】A
10.【答案】B
11.【答案】6
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】6
19.【答案】(1)解:
(2)解:
(3)解:
20.【答案】(1)证明:四边形是平行四边形,,分别为边,上的高,
,
,
,
;
(2)解:①证明:在上取一点,使得,连接,
,
,
,
,
,
,
,
在和中,
,
,
,,
,
,
,
;
②四边形是平行四边形,,分别为边,上的高,
,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
,
,
,即,
解得:,,
,
,
,,
.
21.【答案】(1)证明:分别是AC,AB的中点,
;
分别是OB,OC的中点,
;
四边形EFGH是平行四边形.
(2)解:在中,
是菱形,
,
分别是AB,OB的中点,
.
22.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠EDH=∠FBG,
∵E、F分别为AD,BC的中点,
∴DE=AE=AD,BF=CF=BC,
∴DE=BF,
在△DHE和△BGF中,
,
∴△DHE≌△BGF(SAS),
∴EH=FG,∠EHD=∠FGB,
∴EH∥FG,
∴四边形EHFG是平行四边形.
(2)解:如图②,设AC交EH于点L,连接OF,
∵OH=BH,CF=BF,
∴FH∥AC,
∵AC⊥EH,
∴∠FHE=∠ALH=90°,
∴四边形EHFG是矩形,
∴∠GFH=90°,
∵OG=OH=2,
∴OF=OG=GH=2,
∵CO=AO,CF=BF,
∴AB=2OF=2×2=4,
∴AB的长是4.
23.【答案】(1)
(2)解:当点P在线段上时,如图2,∵,
∴,
由题意可知:,,
又∵,
∴,
当四边形为平行四边形,则有,即,
解得;
当点P在线段的延长线上时,如图3,同上可知:,,,
∴,
∵四边形为平行四边形,
∴,即,
解得,即点Q与点C重合,
综上可知,当或14时,以P,Q,A,B为顶点的四边形是平行四边形;
(3)解:①当,如图1由(1)可知,延长交y轴于点D,
∵四边形是平行四边形,
∴,
∵轴,
∴轴,
∴,
∴四边形是矩形,
∴,,
∴,即;
当时,如图4由(1)可知,,则,,
∴,即,
过点Q作于点F,过点Q作于点E,延长交y轴于点D,
∵,
∴四边形是矩形,
∴,,
∵,,
∴四边形是平行四边形,
∴,,
∴,,
∵,,
∴,
∴,
又∵,
∴,
∴,即,
∴,解得,
综上所述,当或10时,使垂直于平行四边形的某一边;
②
24.【答案】(1)解:由题意可得:AB=4,OC=2,
ABDC的面积为8.
(2)解:∵S△MAC= S平行四边形ABDC=8,OC=2,
∴AM=8,
∴M(-9,0)或(7,0)
(3)解:要使以A,P,C,Q为顶点的四边形是平行四边形,则需CP=AQ,
即4- t= t.
∴t= 秒.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
