1.2《整数的运算性质》(教学课件)(共29张PPT)四年级+数学下册+沪教版
文档属性
| 名称 | 1.2《整数的运算性质》(教学课件)(共29张PPT)四年级+数学下册+沪教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 15:03:27 | ||
图片预览





文档简介
(共29张PPT)
整数的运算性质
小学数学·四年级(下)
沪教版·第一单元
通过举例、类比,归纳得出减法、除法的运算性质。
会运用减法、除法运算性质,使一些计算简便。
初步掌握运用观察、猜想、验证等方法来发现减法、除法的性质。培养学生分析、概括的能力。
重
灵活运用减法、除法运算性质简便运算。
理解和归纳减法、除法的运算性质,并运用性质进行简算。
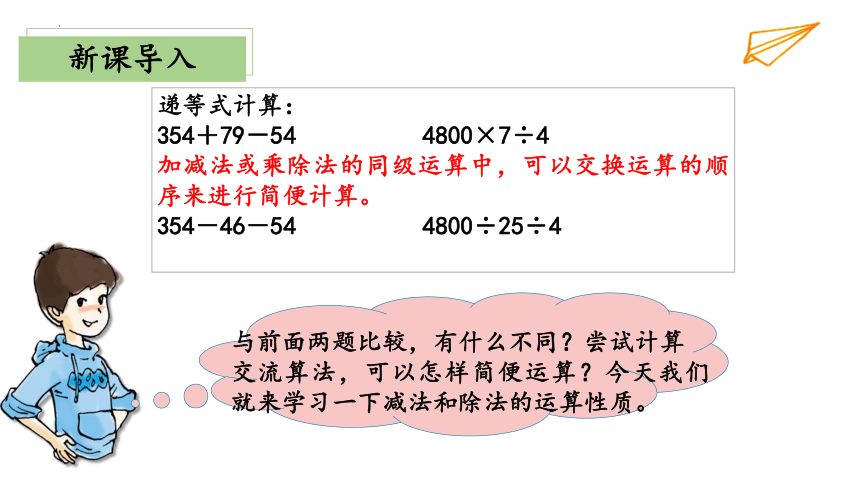
递等式计算:
354+79-54 4800×7÷4
加减法或乘除法的同级运算中,可以交换运算的顺序来进行简便计算。
354-46-54 4800÷25÷4
与前面两题比较,有什么不同?尝试计算
交流算法,可以怎样简便运算?今天我们就来学习一下减法和除法的运算性质。
减法运算性质
小胖
小巧
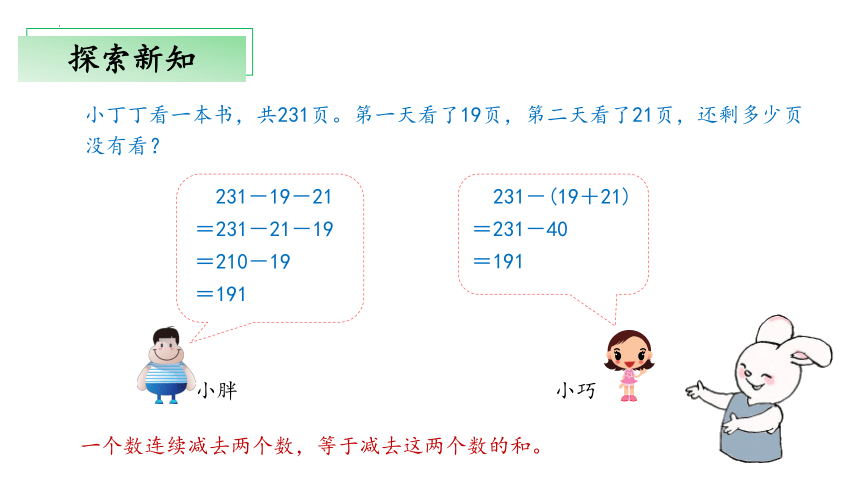
小丁丁看一本书,共231页。第一天看了19页,第二天看了21页,还剩多少页没有看?
231-19-21
=231-21-19
=210-19
=191
一个数连续减去两个数,等于减去这两个数的和。
231-(19+21)
=231-40
=191
举例验证发现性质的正确性
结论:一个数连续减去两个数,可以先把两个减数加起来,再从被减数里减去。这就是减法运算性质,用字母表示为:a-b-c=a-(b+c)
532-127-34=371
532-(127+34)=371
532-127-34=532-(127+34)
785-45-52=688
785-(45+52)=688
785-45-52=785-(45+52)
760-78-22
864-36-64
减法运算性质的应用
当两个减数的和正好是整十、整百、整千……的数时,可以用被减数减去两个减数的和,这样计算比较简便。
=760-(78+22)
=760-100
=660
=864-(36+64)
=864-100
=764
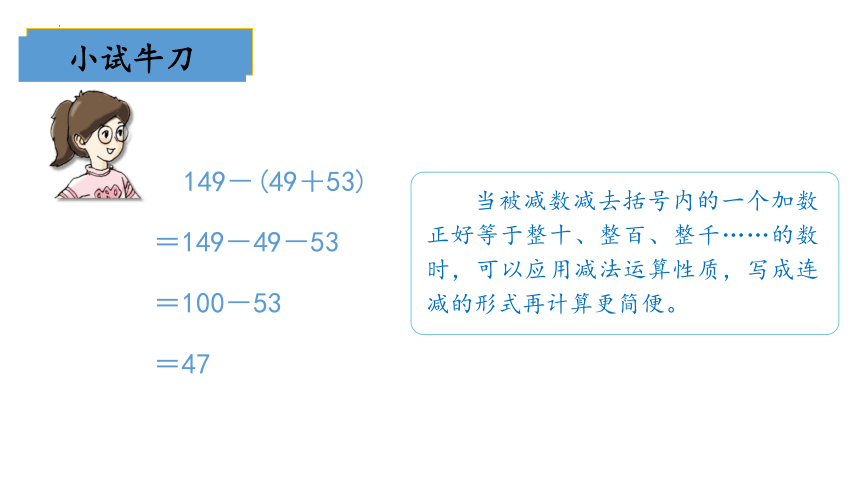
149-(49+53)
=149-49-53
=100-53
=47
当被减数减去括号内的一个加数正好等于整十、整百、整千……的数时,可以应用减法运算性质,写成连减的形式再计算更简便。
减法运算性质:一个数连续减去两个数,可以先把两个减数加起来,再从被减数里减去。用字母表示为:a-b-c=a-(b+c)。
减法运算性质的逆运用:一个数减去两个数的和,可以从这个数里依次减去两个加数。用字母表示为:a-(b+c)=a-b-c。
运用减法运算性质可以使计算简便。
1
2
3
除法运算性质
想一想:一个数连续除以几个数,可以怎样计算?用计算器计算每组算式,你有什么发现?
68÷17÷2=68÷(17×2)
832÷16÷26=832÷(16×26)
3264÷64÷51=3264÷(64×51)
72000÷25÷40=72000÷(25×40)
发现:一个数连续除以两个数,等于除以两个数的积。
结论:一个数连续除以两个数,可以先把两个除数乘起来,再去除被除数。字母表示为:a÷b÷c=a÷(b×c)(b≠0,c≠0)。
除法运算性质的应用
72000÷125÷8
4500÷(30×75)
=72000÷(125×8)
=72000÷1000
=72
=4500÷30÷75
=150÷75
=2
当两个除数的积正好是整十、整百、整千……的数时,可以用被除数除以两个除数的积,计算比较简便。
当被除数除以括号内的一个因数正好等于整十、整百、整千…的数时,可以用被除数先除以这个因数,再除以另一个因数,写成连除的形式计算更简便。
除法运算性质:一个数连续除以两个数,可以先把两个除数乘起来,再去除被除数。
除法运算性质的逆运用:一个数除以两个数的积,等于这个数依次除以两个因数。
1
2
商不变性质
请你写出几个商是2的算式。
根据乘法口诀写出商是2的算式
2÷1=2
4÷2=2
6÷3=2
8÷4=2
10÷5=2
用推算的方法写出商是2的算式
2÷1=2
20÷10=2
200÷100=2
2000÷1000=2
观察上面的算式,算式中的什么数有变化 什么数没有变化
被除数、除数的变化有什么规律 填在下面的表格中
发现:被除数和除数同时乘或者除以一个相同的数(零除外),商不变。
列表对比观察算式中各数之间的变化。
观察算式
被除数的变化
除数的变化
商的变化
2÷1 =2
4÷2 =2
×2
×2
不变
2÷1 =2
6÷3 =2
×3
×3
不变
2÷1 =2
8÷4 =2
×4
×4
不变
4÷2 =2
20÷10 =2
×5
×5
不变
20÷10 =2
2÷1 =2
÷10
÷10
不变
2000÷1000 =2
2÷1 =2
÷1000
÷1000
不变
216÷8=27
结论:被除数和除数同时乘或者除以一个相同的数(零除外),它们的商不变。这叫做商不变性质。
(216× 6 )÷(8× 6 )=27
(216÷ 4 )÷(8÷ 4 )=27
用字母表示为:a÷b=(a c)÷(b c)(b≠c,c≠0)
×
÷
×
÷
商不变性质的应用
结论:当除数乘或者除以一个数可以得到整百、整千……或便于计算的数时,可以运用商不变性质进行凑整,使计算简便。
49000÷125
14000÷350
=(49000×8)÷(125×8)
=392000÷1000
=392
=(14000÷70)÷(350÷70)
=200÷5
=40
计算下面一组题,你有什么发现?
7÷2
70÷20
700÷200
7000÷2000
被除数的变化
除数的变化
商的变化
余数的变化
发现:在有余数的除法中,被除数和除数同时乘或者除以一个相同的数(零除外),它们的商不变,但余数也要随之乘或者除以相同的数。
观察算式
被除数的变化
除数的变化
商的变化
7÷2 =3……1
70÷20 =3……10
×10
×10
不变
余数的变化
×10
7÷2 =3……1
700÷200 =3……100
×100
×100
不变
×100
7÷2 =3……1
7000÷2000 =3……1000
×1000
×1000
不变
×1000
商不变性质:被除数和除数同时乘或者除以一个相同的数(零除外),它们的商不变。用字母表示:a÷b=(a c)÷(b c)(b≠0,c≠0)
在有余数的除法中,被除数和除数同时乘或者除以相同的数(零除外),它们的商不变,但余数也要随之乘或者除以相同的数。
×
÷
×
÷
1
2
14700 ÷ 500
1 4 7 0 0
500
2
1 0
4
7
9
4 5
2
0
0
0
0
=29
......
2000
被除数和除数同时扩大10倍,商不变,余数
也要扩大10倍。
1470 ÷ 50
1 4 7 0
50
2
1 0
4
7
9
4 5
2
0
0
0
0
=29
……
20
被除数和除数同时缩小10倍,商不变,余数
也要缩小10倍。
判断
(1)在360÷50=7……10中,被除数和
除数同时除以10,商和余数都不变。
(2)在6×60=360中,两个因数都乘
10,积不变。
(3)38除以9,商是4,余数是2,如果把
被除数和除数都扩大10倍,那么商是4,
余数是2。
×
×
×
选 择
(1)4800÷700=( )
A. 6……6 B. 6……600
C. 600……6 D. 600……600
(2)被除数乘4,除数除以4,商就 ( )
A. 不变 B. 乘4
C. 除以4 D. 乘16
B
D
选 择
(3)3600÷170=21……30,如果被除数和除数都乘以10,余数是( )
A. 300 B. 30
C. 3 D. 17
(4)在120÷40中,如果被除数增加到360,要使商不变,除数应( )
A. 增加到360 B. 增加360
C. 增加到80 D. 增加80
A
D
作业:
(1)4500÷700
(2)93000÷160
用竖式计算并检验
用递等式巧算
(1)81000÷125
(2)6000÷250
(3)810÷45
Thank you!
整数的运算性质
小学数学·四年级(下)
沪教版·第一单元
通过举例、类比,归纳得出减法、除法的运算性质。
会运用减法、除法运算性质,使一些计算简便。
初步掌握运用观察、猜想、验证等方法来发现减法、除法的性质。培养学生分析、概括的能力。
重
灵活运用减法、除法运算性质简便运算。
理解和归纳减法、除法的运算性质,并运用性质进行简算。
递等式计算:
354+79-54 4800×7÷4
加减法或乘除法的同级运算中,可以交换运算的顺序来进行简便计算。
354-46-54 4800÷25÷4
与前面两题比较,有什么不同?尝试计算
交流算法,可以怎样简便运算?今天我们就来学习一下减法和除法的运算性质。
减法运算性质
小胖
小巧
小丁丁看一本书,共231页。第一天看了19页,第二天看了21页,还剩多少页没有看?
231-19-21
=231-21-19
=210-19
=191
一个数连续减去两个数,等于减去这两个数的和。
231-(19+21)
=231-40
=191
举例验证发现性质的正确性
结论:一个数连续减去两个数,可以先把两个减数加起来,再从被减数里减去。这就是减法运算性质,用字母表示为:a-b-c=a-(b+c)
532-127-34=371
532-(127+34)=371
532-127-34=532-(127+34)
785-45-52=688
785-(45+52)=688
785-45-52=785-(45+52)
760-78-22
864-36-64
减法运算性质的应用
当两个减数的和正好是整十、整百、整千……的数时,可以用被减数减去两个减数的和,这样计算比较简便。
=760-(78+22)
=760-100
=660
=864-(36+64)
=864-100
=764
149-(49+53)
=149-49-53
=100-53
=47
当被减数减去括号内的一个加数正好等于整十、整百、整千……的数时,可以应用减法运算性质,写成连减的形式再计算更简便。
减法运算性质:一个数连续减去两个数,可以先把两个减数加起来,再从被减数里减去。用字母表示为:a-b-c=a-(b+c)。
减法运算性质的逆运用:一个数减去两个数的和,可以从这个数里依次减去两个加数。用字母表示为:a-(b+c)=a-b-c。
运用减法运算性质可以使计算简便。
1
2
3
除法运算性质
想一想:一个数连续除以几个数,可以怎样计算?用计算器计算每组算式,你有什么发现?
68÷17÷2=68÷(17×2)
832÷16÷26=832÷(16×26)
3264÷64÷51=3264÷(64×51)
72000÷25÷40=72000÷(25×40)
发现:一个数连续除以两个数,等于除以两个数的积。
结论:一个数连续除以两个数,可以先把两个除数乘起来,再去除被除数。字母表示为:a÷b÷c=a÷(b×c)(b≠0,c≠0)。
除法运算性质的应用
72000÷125÷8
4500÷(30×75)
=72000÷(125×8)
=72000÷1000
=72
=4500÷30÷75
=150÷75
=2
当两个除数的积正好是整十、整百、整千……的数时,可以用被除数除以两个除数的积,计算比较简便。
当被除数除以括号内的一个因数正好等于整十、整百、整千…的数时,可以用被除数先除以这个因数,再除以另一个因数,写成连除的形式计算更简便。
除法运算性质:一个数连续除以两个数,可以先把两个除数乘起来,再去除被除数。
除法运算性质的逆运用:一个数除以两个数的积,等于这个数依次除以两个因数。
1
2
商不变性质
请你写出几个商是2的算式。
根据乘法口诀写出商是2的算式
2÷1=2
4÷2=2
6÷3=2
8÷4=2
10÷5=2
用推算的方法写出商是2的算式
2÷1=2
20÷10=2
200÷100=2
2000÷1000=2
观察上面的算式,算式中的什么数有变化 什么数没有变化
被除数、除数的变化有什么规律 填在下面的表格中
发现:被除数和除数同时乘或者除以一个相同的数(零除外),商不变。
列表对比观察算式中各数之间的变化。
观察算式
被除数的变化
除数的变化
商的变化
2÷1 =2
4÷2 =2
×2
×2
不变
2÷1 =2
6÷3 =2
×3
×3
不变
2÷1 =2
8÷4 =2
×4
×4
不变
4÷2 =2
20÷10 =2
×5
×5
不变
20÷10 =2
2÷1 =2
÷10
÷10
不变
2000÷1000 =2
2÷1 =2
÷1000
÷1000
不变
216÷8=27
结论:被除数和除数同时乘或者除以一个相同的数(零除外),它们的商不变。这叫做商不变性质。
(216× 6 )÷(8× 6 )=27
(216÷ 4 )÷(8÷ 4 )=27
用字母表示为:a÷b=(a c)÷(b c)(b≠c,c≠0)
×
÷
×
÷
商不变性质的应用
结论:当除数乘或者除以一个数可以得到整百、整千……或便于计算的数时,可以运用商不变性质进行凑整,使计算简便。
49000÷125
14000÷350
=(49000×8)÷(125×8)
=392000÷1000
=392
=(14000÷70)÷(350÷70)
=200÷5
=40
计算下面一组题,你有什么发现?
7÷2
70÷20
700÷200
7000÷2000
被除数的变化
除数的变化
商的变化
余数的变化
发现:在有余数的除法中,被除数和除数同时乘或者除以一个相同的数(零除外),它们的商不变,但余数也要随之乘或者除以相同的数。
观察算式
被除数的变化
除数的变化
商的变化
7÷2 =3……1
70÷20 =3……10
×10
×10
不变
余数的变化
×10
7÷2 =3……1
700÷200 =3……100
×100
×100
不变
×100
7÷2 =3……1
7000÷2000 =3……1000
×1000
×1000
不变
×1000
商不变性质:被除数和除数同时乘或者除以一个相同的数(零除外),它们的商不变。用字母表示:a÷b=(a c)÷(b c)(b≠0,c≠0)
在有余数的除法中,被除数和除数同时乘或者除以相同的数(零除外),它们的商不变,但余数也要随之乘或者除以相同的数。
×
÷
×
÷
1
2
14700 ÷ 500
1 4 7 0 0
500
2
1 0
4
7
9
4 5
2
0
0
0
0
=29
......
2000
被除数和除数同时扩大10倍,商不变,余数
也要扩大10倍。
1470 ÷ 50
1 4 7 0
50
2
1 0
4
7
9
4 5
2
0
0
0
0
=29
……
20
被除数和除数同时缩小10倍,商不变,余数
也要缩小10倍。
判断
(1)在360÷50=7……10中,被除数和
除数同时除以10,商和余数都不变。
(2)在6×60=360中,两个因数都乘
10,积不变。
(3)38除以9,商是4,余数是2,如果把
被除数和除数都扩大10倍,那么商是4,
余数是2。
×
×
×
选 择
(1)4800÷700=( )
A. 6……6 B. 6……600
C. 600……6 D. 600……600
(2)被除数乘4,除数除以4,商就 ( )
A. 不变 B. 乘4
C. 除以4 D. 乘16
B
D
选 择
(3)3600÷170=21……30,如果被除数和除数都乘以10,余数是( )
A. 300 B. 30
C. 3 D. 17
(4)在120÷40中,如果被除数增加到360,要使商不变,除数应( )
A. 增加到360 B. 增加360
C. 增加到80 D. 增加80
A
D
作业:
(1)4500÷700
(2)93000÷160
用竖式计算并检验
用递等式巧算
(1)81000÷125
(2)6000÷250
(3)810÷45
Thank you!
