浙教版八年级数学上册试题 第2章 特殊三角形 单元复习题(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 第2章 特殊三角形 单元复习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 767.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 11:27:14 | ||
图片预览


文档简介
《特殊三角形》单元复习题
一、单选题
1.下列图形是轴对称图形的是( )
A.B.C.D.
2.如图,△ABC≌△A′B′C,且点B′在AB边上,点A′恰好在BC的延长线上,下列结论错误的是( )
A.∠BCB′=∠ACA′ B.∠ACB=2∠B
C.∠B′CA=∠B′AC D.B′C平分∠BB′A′
3.在中,线段AD,AE,AF分别是的高、中线、角平分线,以下两个结论:①若,则点D,E,F重合;②若,则点F总在点D,E之间,其中( )
A.①是真命题,②是假命题 B.①是假命题,②是真命题
C.①②均是假命题 D.①②均是真命题
4.如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45° B.55° C.60° D.75°
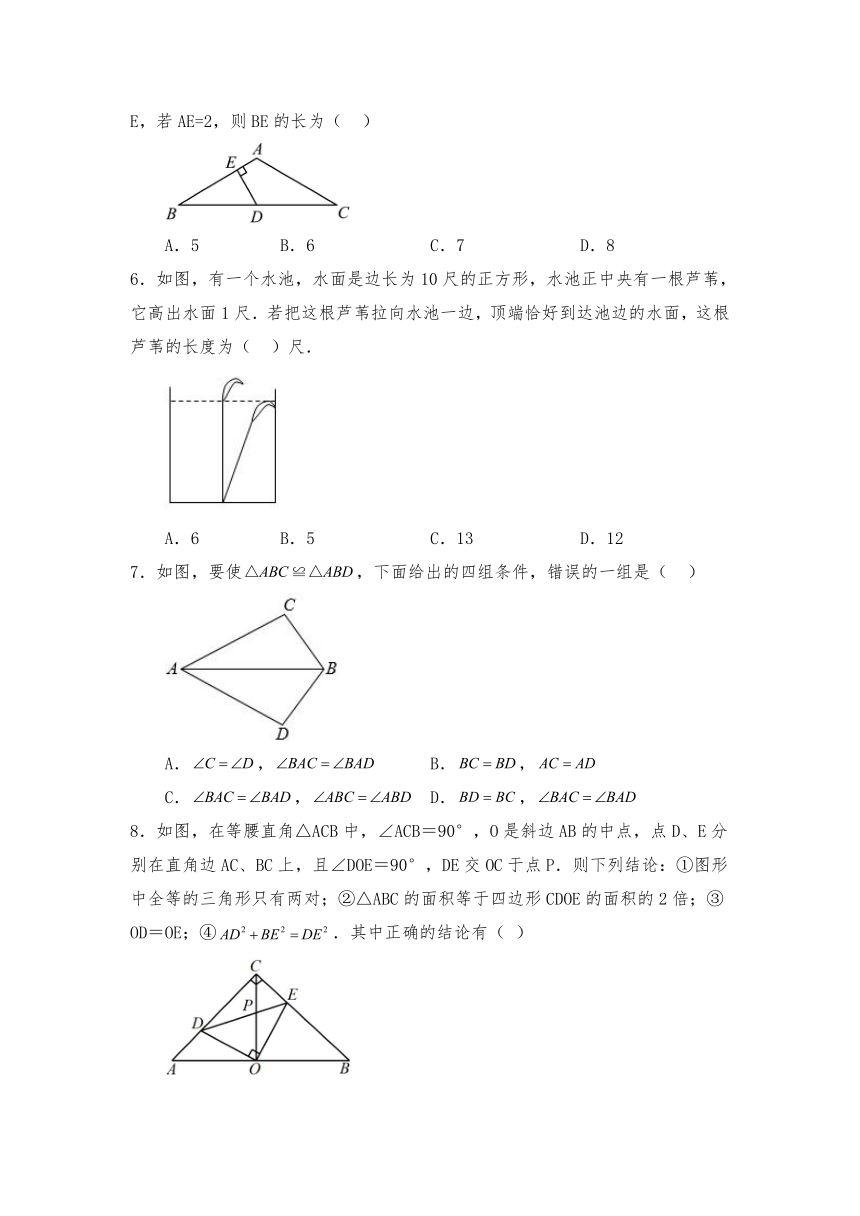
5.如图,已知:在△ABC中,AB=AC,∠A=120°,D为BC的中点,DE⊥AB于点E,若AE=2,则BE的长为( )
A.5 B.6 C.7 D.8
6.如图,有一个水池,水面是边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边,顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.6 B.5 C.13 D.12
7.如图,要使,下面给出的四组条件,错误的一组是( )
A., B.,
C., D.,
8.如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①图形中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的2倍;③OD=OE;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
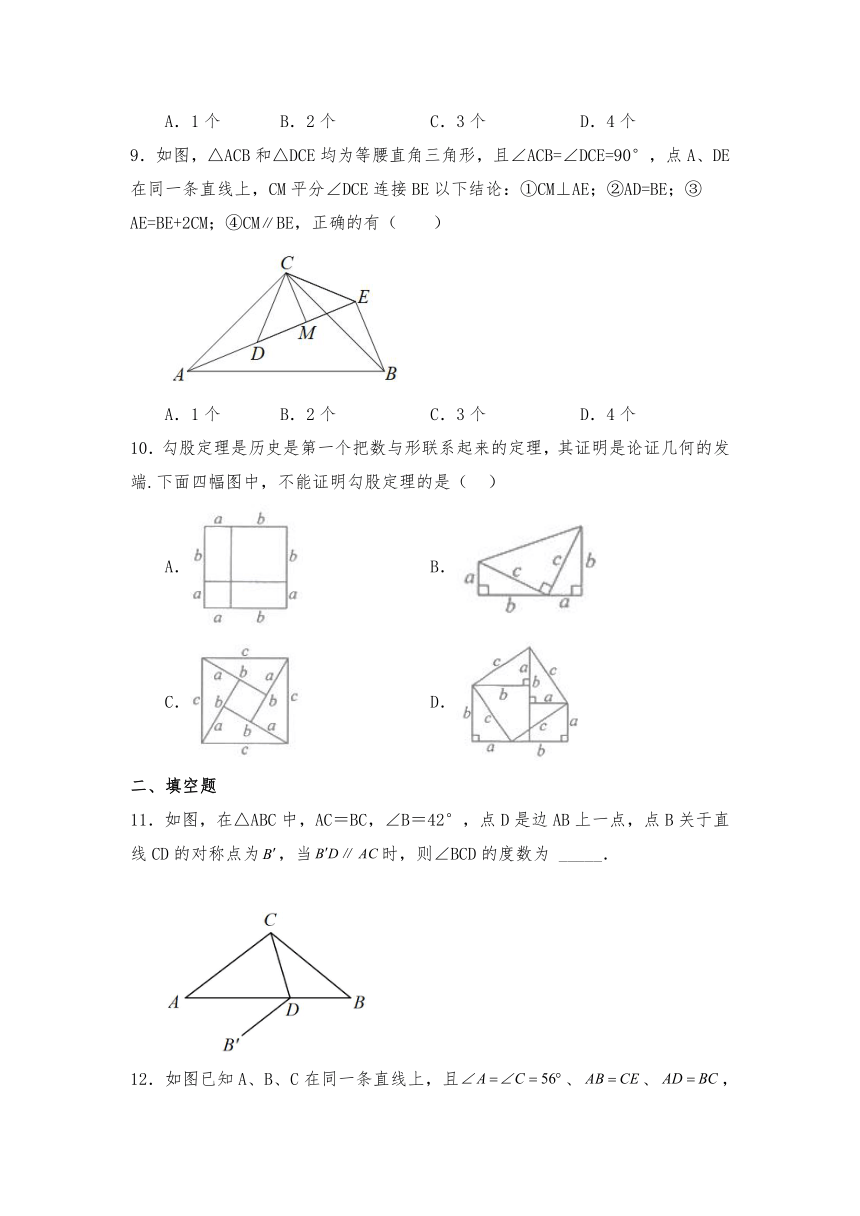
9.如图,△ACB和△DCE均为等腰直角三角形,且∠ACB=∠DCE=90°,点A、DE在同一条直线上,CM平分∠DCE连接BE以下结论:①CM⊥AE;②AD=BE;③AE=BE+2CM;④CMBE,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.勾股定理是历史是第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B.
C. D.
二、填空题
11.如图,在△ABC中,AC=BC,∠B=42°,点D是边AB上一点,点B关于直线CD的对称点为,当时,则∠BCD的度数为 _____.
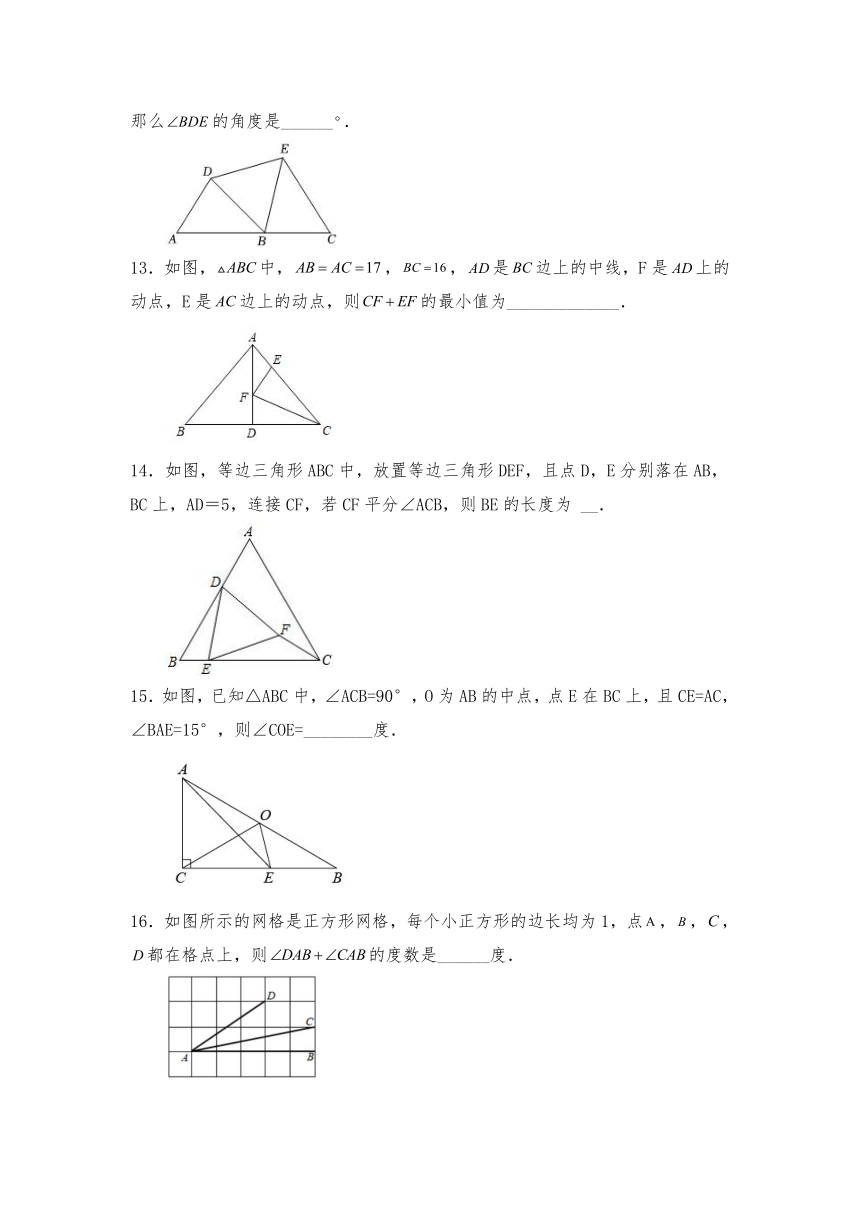
12.如图已知A、B、C在同一条直线上,且、、,那么的角度是______.
13.如图,中,,,是边上的中线,F是上的动点,E是边上的动点,则的最小值为_____________.
14.如图,等边三角形ABC中,放置等边三角形DEF,且点D,E分别落在AB,BC上,AD=5,连接CF,若CF平分∠ACB,则BE的长度为 __.
15.如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E在BC上,且CE=AC,∠BAE=15°,则∠COE=________度.
16.如图所示的网格是正方形网格,每个小正方形的边长均为1,点,,,都在格点上,则的度数是______度.
17.如图,中,,平分交于点,交的延长线于点,交于点.若,,.则的长为_________.
18.如图,中,平分,、分别是的两外角的平分线,射线的反向延长线交于点P,下列结论中:①;②;③;④;⑤.其中正确的结论是___________(直接填写序号).
三、解答题
19.如图,在若干个长度为的小正方形组成的网格中,点,,在小正方形的顶点上.
(1) 在图中画出与关于直线成轴对称的;
(2) 求的面积;
(3) 在直线上找到一点,使的长最短,在图中标出这一点的位置.
20.如图,在中,,.
(1)通过观察尺规作图的痕迹,可以发现直线是线段的__________,射线是的__________;
(2)在(1)所作的图中,求的度数.
21.如图,在ABC中,∠C=90 ,BD是ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
22.如图,点P、Q分别是等边边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连接AQ、CP求证:
(2)如图1,当点P、Q分别在AB、BC边上运动时,AQ、CP相交于点M,的大小是否变化?若变化,请说明理由;若不变,求出它的度数
(3)如图2,当点P、Q在AB、BC的延长线上运动时,直线AQ、CP相交于M,的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
23.在中,,D为内一点,连接,,延长到点,使得
(1)如图1,延长到点,使得,连接,,若,求证:;
(2)连接,交的延长线于点,连接,依题意补全图2,若,用等式表示线段与的数量关系,并证明.
24.两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:
如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
图1
(2)解决问题:如图2,若和均为等腰直角三角形,,点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图2
25.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
(1)如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
(2)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
答案
一、单选题
1.C 2.C 3.D 4.C 5.B 6.C 7.D 8.C 9.D 10.A
二、填空题
11.27°
12.62
13.
14.2.5
15.75
16.
17.8
18.①②④⑤
三、解答题
19.(1)解:如图所示,点,,关于直线的对称点分别为点,,,
连接,,,
∴即为所作.
(2)
.
(3)连接,与直线交于点,
∵点与点关于直线对称,
∴,
∴,
∴当点,,共线时,的长最短,即的长最短,
∴点即为所作.
20.解:(1)由图可知:直线是线段的垂直平分线,射线是的角平分线,
故答案为:垂直平分线,角平分线;
(2)∵是线段的垂直平分线,
∴,
∴,
∵,,
∴,
∴.
∵射线是的平分线,
∴.
21.
解:(1)过点O作OM⊥AB于点M
∵正方形OECF
∴OE=EC=CF=OF,OE⊥BC于E,OF⊥AC于F
∵BD平分∠ABC,OM⊥AB于M,OE⊥BC于E
∴OM=OE=OF
∵OM⊥AB于M, OE⊥BC于E
∴∠AMO=90°,∠AFO=90°
∵
∴Rt△AMO≌Rt△AFO
∴∠MA0=∠FAO
∴点O在∠BAC的平分线上
(2)∵Rt△ABC中,∠C=90°,AC=5,BC=12
∴AB=13
∴BE=BM,AM=AF
又BE=BC-CE,AF=AC-CF,而CE=CF=OE
∴BE=12-OE,AF=5-OE
∴BM+AM=AB
即BE+AF=13
12-OE+5-OE=13
解得OE=2
22.
解:(1)证明:∵三角形ABC为等边三角形,
∴AB=AC,∠ABC=∠CAB=60°,
∵点P、点Q以相同的速度,同时从点A、点B出发,
∴BQ=AP,
在△ABQ与△CAB中,
∴.
(2)角度不变,60°,理由如下:
∵
∴∠CPA=∠AQB,
在△AMP中,
∠AMP=180°-(∠MAP+∠CPA)=180°-(∠MAP+∠AQB)=∠ABC=60°,
∴∠QMC=∠AMP=60°,
故∠QMC的度数不变,度数为60°.
(3)角度不变,120°,理由如下:
当点P、Q在AB、BC的延长线上运动时,
有AP=BQ,∴BP=CQ
∵∠ABC=∠BCA=60°,
∴∠CBP=∠ACQ=120°,
∴
∴∠Q=∠P,
∵∠QCM=∠BCP,
∴∠QMC=∠CBP=120°,
故∠QMC的度数不变,度数为120°.
23.(1)证明:在和中,
,
∴ ,
∴ ,
∴ ,
∵,
∴.
(2)解:补全后的图形如图所示,,证明如下:
延长BC到点M,使CM=CB,连接EM,AM,
∵,CM=CB,
∴ 垂直平分BM,
∴,
在和中,
,
∴ ,
∴ ,∠CME=∠CBD,
∵,
∴ ,
∴ ,
∵∠CME=∠CBD,
∴,
∴∠BHE=∠AEM=900 ,即,
∵,
∴ ,
∴ .
24.
(1)证明:∵和是顶角相等的等腰三角形,
∴,,,
∴,
∴.
在和中,
,
∴,
∴.
(2)解:,,
理由如下:由(1)的方法得,,
∴,,
∵是等腰直角三角形,
∴,
∴,
∴,
∴.
∵,,
∴.
∵,
∴,
∴.
∴.
25.
解:(1)证明:在CD上截取CH=CE,如图1所示:
∵△ABC是等边三角形,
∴∠ECH=60°,
∴△CEH是等边三角形,
∴EH=EC=CH,∠CEH=60°,
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,
∴∠DEH=∠FEC,
在△DEH和△FEC中,
,
∴△DEH≌△FEC(SAS),
∴DH=CF,
∴CD=CH+DH=CE+CF,
∴CE+CF=CD;
(2)解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60°,
过D作DG∥AB,交AC的延长线于点G,如图2所示:
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴△GCD为等边三角形,
∴DG=CD=CG,∠GDC=60°,
∵△EDF为等边三角形,
∴ED=DF,∠EDF=∠GDC=60°,
∴∠EDG=∠FDC,
在△EGD和△FCD中,
,
∴△EGD≌△FCD(SAS),
∴EG=FC,
∴FC=EG=CG+CE=CD+CE.
一、单选题
1.下列图形是轴对称图形的是( )
A.B.C.D.
2.如图,△ABC≌△A′B′C,且点B′在AB边上,点A′恰好在BC的延长线上,下列结论错误的是( )
A.∠BCB′=∠ACA′ B.∠ACB=2∠B
C.∠B′CA=∠B′AC D.B′C平分∠BB′A′
3.在中,线段AD,AE,AF分别是的高、中线、角平分线,以下两个结论:①若,则点D,E,F重合;②若,则点F总在点D,E之间,其中( )
A.①是真命题,②是假命题 B.①是假命题,②是真命题
C.①②均是假命题 D.①②均是真命题
4.如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45° B.55° C.60° D.75°
5.如图,已知:在△ABC中,AB=AC,∠A=120°,D为BC的中点,DE⊥AB于点E,若AE=2,则BE的长为( )
A.5 B.6 C.7 D.8
6.如图,有一个水池,水面是边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边,顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.6 B.5 C.13 D.12
7.如图,要使,下面给出的四组条件,错误的一组是( )
A., B.,
C., D.,
8.如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①图形中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的2倍;③OD=OE;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
9.如图,△ACB和△DCE均为等腰直角三角形,且∠ACB=∠DCE=90°,点A、DE在同一条直线上,CM平分∠DCE连接BE以下结论:①CM⊥AE;②AD=BE;③AE=BE+2CM;④CMBE,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.勾股定理是历史是第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B.
C. D.
二、填空题
11.如图,在△ABC中,AC=BC,∠B=42°,点D是边AB上一点,点B关于直线CD的对称点为,当时,则∠BCD的度数为 _____.
12.如图已知A、B、C在同一条直线上,且、、,那么的角度是______.
13.如图,中,,,是边上的中线,F是上的动点,E是边上的动点,则的最小值为_____________.
14.如图,等边三角形ABC中,放置等边三角形DEF,且点D,E分别落在AB,BC上,AD=5,连接CF,若CF平分∠ACB,则BE的长度为 __.
15.如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E在BC上,且CE=AC,∠BAE=15°,则∠COE=________度.
16.如图所示的网格是正方形网格,每个小正方形的边长均为1,点,,,都在格点上,则的度数是______度.
17.如图,中,,平分交于点,交的延长线于点,交于点.若,,.则的长为_________.
18.如图,中,平分,、分别是的两外角的平分线,射线的反向延长线交于点P,下列结论中:①;②;③;④;⑤.其中正确的结论是___________(直接填写序号).
三、解答题
19.如图,在若干个长度为的小正方形组成的网格中,点,,在小正方形的顶点上.
(1) 在图中画出与关于直线成轴对称的;
(2) 求的面积;
(3) 在直线上找到一点,使的长最短,在图中标出这一点的位置.
20.如图,在中,,.
(1)通过观察尺规作图的痕迹,可以发现直线是线段的__________,射线是的__________;
(2)在(1)所作的图中,求的度数.
21.如图,在ABC中,∠C=90 ,BD是ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
22.如图,点P、Q分别是等边边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连接AQ、CP求证:
(2)如图1,当点P、Q分别在AB、BC边上运动时,AQ、CP相交于点M,的大小是否变化?若变化,请说明理由;若不变,求出它的度数
(3)如图2,当点P、Q在AB、BC的延长线上运动时,直线AQ、CP相交于M,的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
23.在中,,D为内一点,连接,,延长到点,使得
(1)如图1,延长到点,使得,连接,,若,求证:;
(2)连接,交的延长线于点,连接,依题意补全图2,若,用等式表示线段与的数量关系,并证明.
24.两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:
如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
图1
(2)解决问题:如图2,若和均为等腰直角三角形,,点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图2
25.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
(1)如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
(2)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
答案
一、单选题
1.C 2.C 3.D 4.C 5.B 6.C 7.D 8.C 9.D 10.A
二、填空题
11.27°
12.62
13.
14.2.5
15.75
16.
17.8
18.①②④⑤
三、解答题
19.(1)解:如图所示,点,,关于直线的对称点分别为点,,,
连接,,,
∴即为所作.
(2)
.
(3)连接,与直线交于点,
∵点与点关于直线对称,
∴,
∴,
∴当点,,共线时,的长最短,即的长最短,
∴点即为所作.
20.解:(1)由图可知:直线是线段的垂直平分线,射线是的角平分线,
故答案为:垂直平分线,角平分线;
(2)∵是线段的垂直平分线,
∴,
∴,
∵,,
∴,
∴.
∵射线是的平分线,
∴.
21.
解:(1)过点O作OM⊥AB于点M
∵正方形OECF
∴OE=EC=CF=OF,OE⊥BC于E,OF⊥AC于F
∵BD平分∠ABC,OM⊥AB于M,OE⊥BC于E
∴OM=OE=OF
∵OM⊥AB于M, OE⊥BC于E
∴∠AMO=90°,∠AFO=90°
∵
∴Rt△AMO≌Rt△AFO
∴∠MA0=∠FAO
∴点O在∠BAC的平分线上
(2)∵Rt△ABC中,∠C=90°,AC=5,BC=12
∴AB=13
∴BE=BM,AM=AF
又BE=BC-CE,AF=AC-CF,而CE=CF=OE
∴BE=12-OE,AF=5-OE
∴BM+AM=AB
即BE+AF=13
12-OE+5-OE=13
解得OE=2
22.
解:(1)证明:∵三角形ABC为等边三角形,
∴AB=AC,∠ABC=∠CAB=60°,
∵点P、点Q以相同的速度,同时从点A、点B出发,
∴BQ=AP,
在△ABQ与△CAB中,
∴.
(2)角度不变,60°,理由如下:
∵
∴∠CPA=∠AQB,
在△AMP中,
∠AMP=180°-(∠MAP+∠CPA)=180°-(∠MAP+∠AQB)=∠ABC=60°,
∴∠QMC=∠AMP=60°,
故∠QMC的度数不变,度数为60°.
(3)角度不变,120°,理由如下:
当点P、Q在AB、BC的延长线上运动时,
有AP=BQ,∴BP=CQ
∵∠ABC=∠BCA=60°,
∴∠CBP=∠ACQ=120°,
∴
∴∠Q=∠P,
∵∠QCM=∠BCP,
∴∠QMC=∠CBP=120°,
故∠QMC的度数不变,度数为120°.
23.(1)证明:在和中,
,
∴ ,
∴ ,
∴ ,
∵,
∴.
(2)解:补全后的图形如图所示,,证明如下:
延长BC到点M,使CM=CB,连接EM,AM,
∵,CM=CB,
∴ 垂直平分BM,
∴,
在和中,
,
∴ ,
∴ ,∠CME=∠CBD,
∵,
∴ ,
∴ ,
∵∠CME=∠CBD,
∴,
∴∠BHE=∠AEM=900 ,即,
∵,
∴ ,
∴ .
24.
(1)证明:∵和是顶角相等的等腰三角形,
∴,,,
∴,
∴.
在和中,
,
∴,
∴.
(2)解:,,
理由如下:由(1)的方法得,,
∴,,
∵是等腰直角三角形,
∴,
∴,
∴,
∴.
∵,,
∴.
∵,
∴,
∴.
∴.
25.
解:(1)证明:在CD上截取CH=CE,如图1所示:
∵△ABC是等边三角形,
∴∠ECH=60°,
∴△CEH是等边三角形,
∴EH=EC=CH,∠CEH=60°,
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,
∴∠DEH=∠FEC,
在△DEH和△FEC中,
,
∴△DEH≌△FEC(SAS),
∴DH=CF,
∴CD=CH+DH=CE+CF,
∴CE+CF=CD;
(2)解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60°,
过D作DG∥AB,交AC的延长线于点G,如图2所示:
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴△GCD为等边三角形,
∴DG=CD=CG,∠GDC=60°,
∵△EDF为等边三角形,
∴ED=DF,∠EDF=∠GDC=60°,
∴∠EDG=∠FDC,
在△EGD和△FCD中,
,
∴△EGD≌△FCD(SAS),
∴EG=FC,
∴FC=EG=CG+CE=CD+CE.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
