浙教版八年级数学上册试题第4章 图形与坐标 单元复习题(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题第4章 图形与坐标 单元复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 809.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 11:28:21 | ||
图片预览


文档简介
《图形与坐标》单元复习题
一、单选题
1.对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(﹣a,b),如f(1,2)=(﹣1,2);g(a,b)=(b,a),如g(1,2)=(2,1),据此得g[f(5,﹣9)]=( )
A.(5,﹣9) B.(﹣5,﹣9) C.(﹣9,﹣5) D.(﹣9,5)
2.在平面直角坐标系中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为,点的坐标为( )
A. B. C. D.
3.已知点位于第二象限,并且,a,b均为整数,则满足条件的点A个数有( )
A.4个 B.5个 C.6个 D.7个
4.已知点E(x0,yo),点F(x2.y2),点M(x1,y1)是线段EF的中点,则x1=,y1=.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
A.(4,0) B.(﹣2,2) C.(2,﹣4) D.(﹣4,2)
5.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
6.如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
A.3 B.4 C.5 D.6
7.如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
A. ()2015 B. ()2016 C. ()2017 D. ()2018
8.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是( )
A.M(1,﹣3),N(﹣1,﹣3)
B.M(﹣1,﹣3),N(﹣1,3)
C.M(﹣1,﹣3),N(1,﹣3)
D.M(﹣1,3),N(1,﹣3)
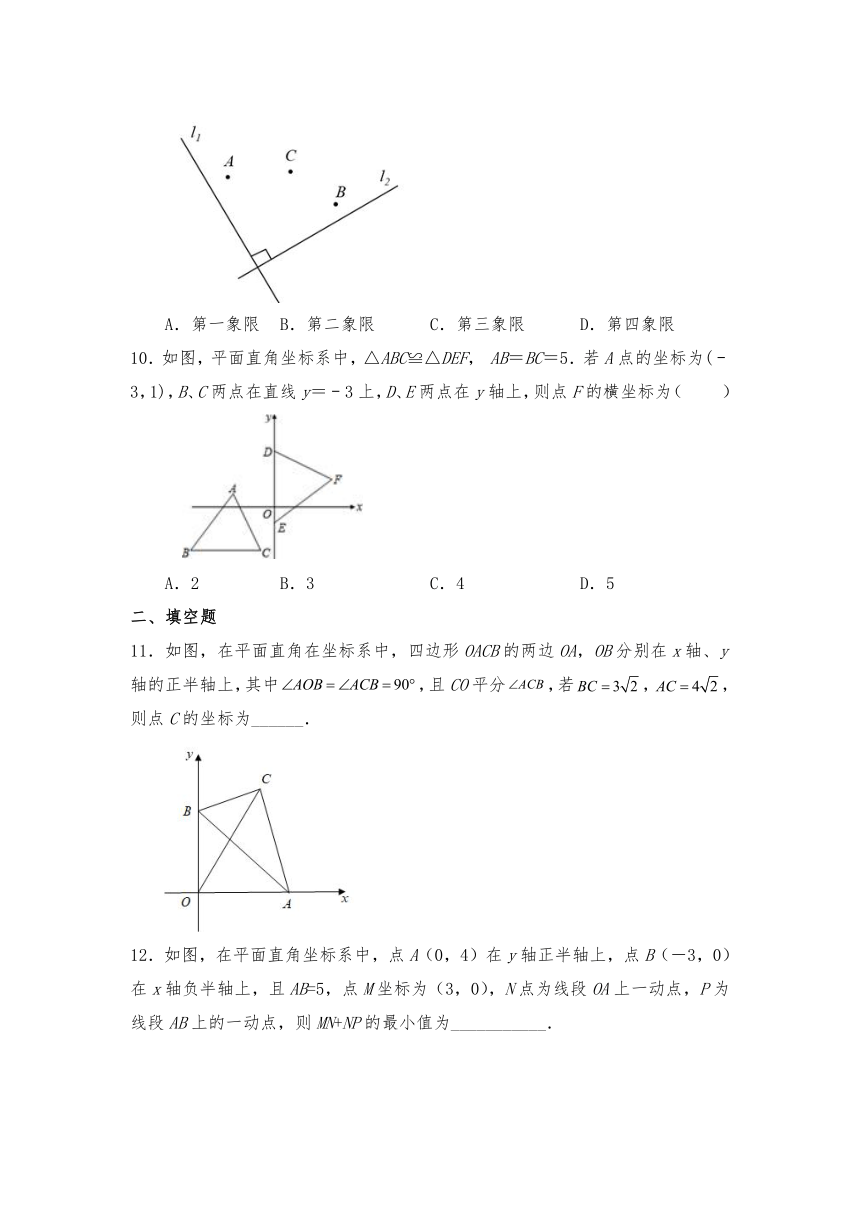
9.如图,已知直线l1⊥l2,且在某平面直角坐标系中, x轴∥l1,y轴∥l2,若点A的坐标为(-1,2),点B的坐标为(2,-1),则点C在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,平面直角坐标系中,△ABC≌△DEF, AB=BC=5.若A点的坐标为(﹣3,1),B、C两点在直线y=﹣3上,D、E两点在y轴上,则点F的横坐标为( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在平面直角在坐标系中,四边形OACB的两边OA,OB分别在x轴、y轴的正半轴上,其中,且CO平分,若,,则点C的坐标为______.
12.如图,在平面直角坐标系中,点A(0,4)在y轴正半轴上,点B(-3,0)在x轴负半轴上,且AB=5,点M坐标为(3,0),N点为线段OA上一动点,P为线段AB上的一动点,则MN+NP的最小值为___________.
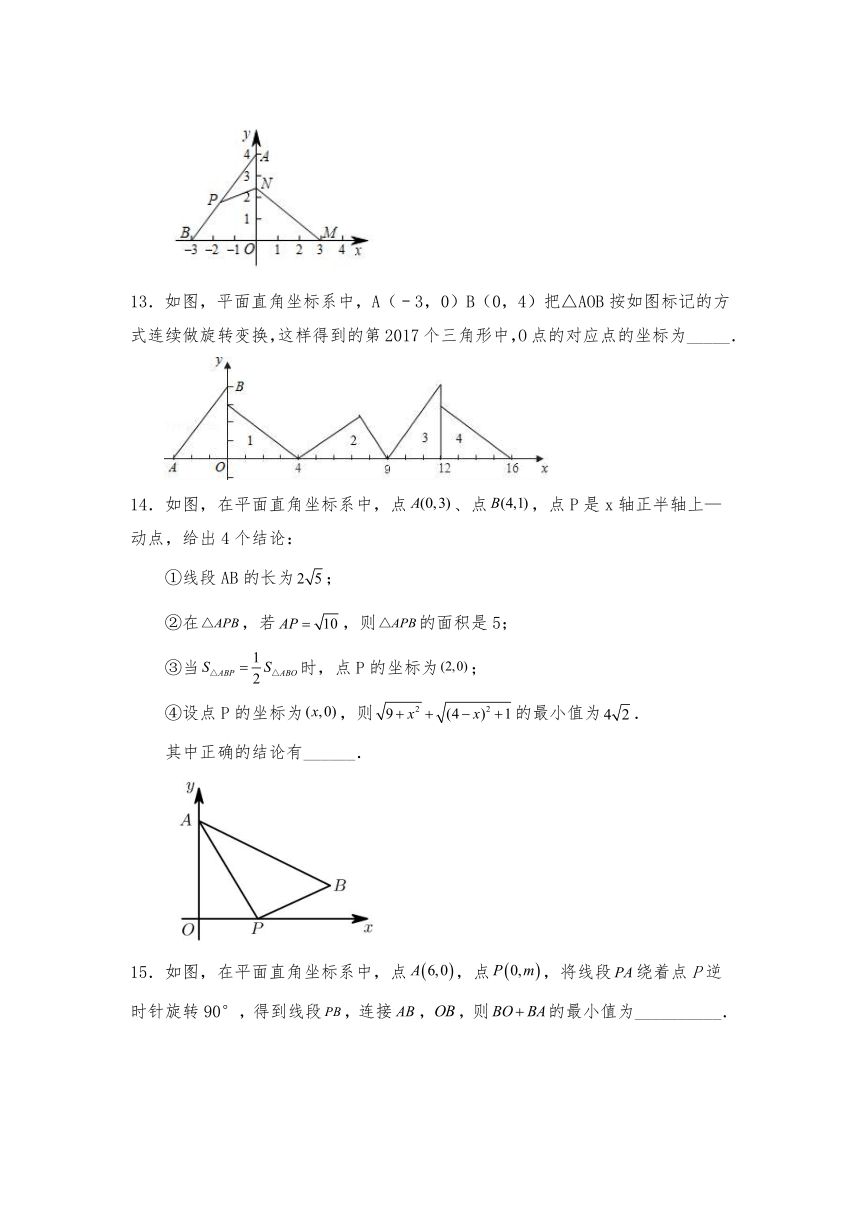
13.如图,平面直角坐标系中,A(﹣3,0)B(0,4)把△AOB按如图标记的方式连续做旋转变换,这样得到的第2017个三角形中,O点的对应点的坐标为_____.
14.如图,在平面直角坐标系中,点、点,点P是x轴正半轴上—动点,给出4个结论:
①线段AB的长为;
②在,若,则的面积是5;
③当时,点P的坐标为;
④设点P的坐标为,则的最小值为.
其中正确的结论有______.
15.如图,在平面直角坐标系中,点,点,将线段绕着点P逆时针旋转90°,得到线段,连接,,则的最小值为__________.
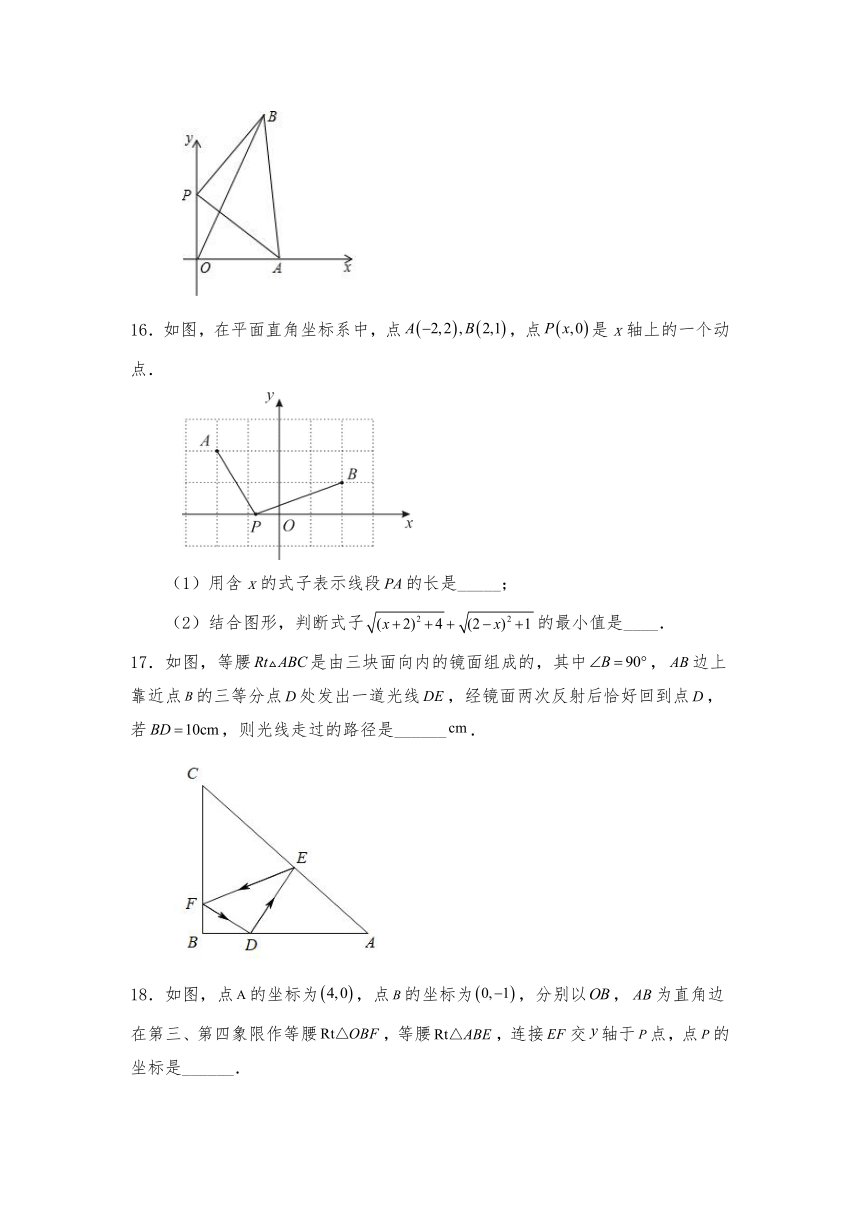
16.如图,在平面直角坐标系中,点,点是x轴上的一个动点.
(1)用含x的式子表示线段的长是_____;
(2)结合图形,判断式子的最小值是____.
17.如图,等腰是由三块面向内的镜面组成的,其中,边上靠近点的三等分点处发出一道光线,经镜面两次反射后恰好回到点,若,则光线走过的路径是______.
18.如图,点的坐标为,点的坐标为,分别以,为直角边在第三、第四象限作等腰,等腰,连接交轴于点,点的坐标是______.
19.如图,在平面直角坐标系中,是边长为的等边三角形,是边上的高,点是上的一个动点,若点的坐标是,则的最小值是________.
20.在平面直角坐标系中,点A(3,0),B(0,6),作△BOC,使△BOC与△ABO全等,则点C坐标为 _______________.
三、解答题
21.在平面直角坐标系中,点A的坐标为,过点作x轴的垂线l,点A与点B关于直线l对称;
(1) 点B的坐标为________;
(2) 点C的坐标为,顺次连接,若在四边形内部有一个点P,满足,且,求点P的坐标;
(3) 在四边形外部是否存在点Q,满足,且,若存在,直接写出Q点坐标,若不存在请说明理由.
22.如图,的顶点A,B分别在x轴,y轴上,;
(1) 若,且点B(0,2),C(-2,-1),
① 点C关于y轴对称点的坐标为______;
② 求点A的坐标;
(2) 若点B与原点重合,时,存在第三象限的点E和y轴上的点F,使,且A(3,0),C(0,m),F(0,n),线段EF的长度为,求AE的长.
23.对于平面内的及其内部的一点,设点到直线,的距离分别为,,称和这两个数中较大的一个为点关于的“偏率”在平面直角坐标系中,点,分别为轴正半轴,轴正半轴上的两个点.
(1) 若点的坐标为,则点关于的“偏率”为______;
(2) 若第一象限内点关于的“偏率”为1,则,满足的关系为______;
(3) 若第一象限内点关于的“偏率”为2.在平面直角坐标系上,画出所有点E形成的图形.
24.如图,在平面直角坐标系中,已知,,其中,满足,点为第三象限内一点.
(1)若到坐标轴的距离相等,,且,求点坐标
(2)若为,请用含的式子表示的面积.
(3)在(2)条件下,当时,在轴上有点,使得的面积是的面积的2倍,请求出点的坐标.
25.已知:在平面直角坐标系中,点在第四象限,且到x轴的距离为2,到y轴的距离为1.
(1) 求点的坐标;
(2) 若轴,且点C到x轴的距离与点A到x轴的距离相等,请直接写出点C的坐标;
(3) 在坐标轴上是否存在一点M,使的面积的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由.
26.如图,在平面直角坐标系中,点A、B的坐标分别为、,且实数a、b满足.
求A、B两点的坐标;
如图1,已知坐标轴上有两动点P,Q同时出发,P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动,点P到达O点整个运动随之结束.AB的中点C的坐标是,设运动时间为t秒.是否存在这样的t,使得的面积等于面积的2倍?若存在,请求出t的值;若不存在,请说明理由;
如图2,在(2)的条件下,若,点G是第二象限中一点,并且y轴平分.点E是线段OB上一动点,连接AE交OC于点H,当点E在线段OB上运动的过程中,探究,,之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
答案
一、单选题
1.C 2.D 3.B 4.B 5.B 6.D 7.B 8.C 9.C 10.C
二、填空题
11.
12.
13.(8064,0)
14.①②④
15.
16. 5
17.
18.
19.
20.或或
三、解答题
21.
解:(1)点A的坐标为,过点作x轴的垂线l,
到的距离为,
则
故答案为:
(2)如图,,,
点与点关于对称,
在四边形内部有一个点P,满足,
则点在上,设点,
,
即
解得或
在四边形内部
(3)存在,由(2)可知时,在四边形外部
故
22.(1)解:(1)①由关于y轴对称的点纵坐标不变、横坐标变为原来的相反数,则点C(-2,-1)关于y轴对称点的坐标为(2,-1);
故答案是(2,-1);
②设A点坐标为(a,0)
∵B(0,2),C(-2,-1),
∴BC=
∴AB=BC=
∴,解得a=3.
∴点A的坐标为(3,0).
(2)解:(2)作点F关于x轴的对称点H(0,-n),则AF=AH、OF=OH,过点H作HN⊥AC于点N,过点F作FM⊥AE于点M,
∵C(0,m),H(0,-n),m<0,n>0,
∴HC=OC-OH=-m-n,
∵EF=-m-n,
∴HC=EF,
∵∠AEF=∠ACO=30°,
∴∠FME=∠HNC,
∴△FEM≌△HCN(AAS),
∴FM=HN,EM=CN,
在Rt△AFM和Rt△AHN中,
AF=AH,FM=HN
∴Rt△AFM≌Rt△AHN(HL),
∴AM=AN,
∴EM+AM=CN+AN,
∴AE=AC,
∵∠ACO=30°,A(3,0),
∴OA=3,
∴AC=2OA=6,
∴AE=6.
23.
(1)解:∵点M,N分别在x轴正半轴,y轴正半轴上,
∴点P(1,5)到OM距离d1=5,到ON距离d2=1,
∴点P关于∠MON的“偏率”为:5;
故答案为:5;
(2)∵点Q(a,b)在第一象限,到OM距离d1=b,到ON距离d2=a,
∴点Q关于∠MON的“偏率”为:1或1,
∴a=b,
故答案为:a=b;
(3)∵点在第一象限,
∴点E到OM距离d1=y,到ON距离d2=x,
又∵点E关于的“偏率”为2,
∴点E关于∠MON的“偏率”为:2或,
即点E在函数或的图象上,
点E形成的图形如图所示:
24.解:(1)由题意可知:
,
求得,
∵,
∴,,
∴,,
∴,
∵,,
∴,
∵,
∴或者,
∴或;
(2)由题意可得:
,
∵在三象限,
∴,
∴;
(3)当时,,
由题意可得:
,
,
,
,
∴或.
25.(1)解:∵点在第四象限,且到x轴的距离为2,到y轴的距离为1,
∴,解得:,
∴,,
∴
(2)解:由(1)可知:,
∵轴,点C到x轴的距离与点A到x轴的距离相等,
∴C的横坐标为1,纵坐标为2,
∴
(3)解:假设存在点M,使得,
∵,,
∴,
∴,
当点M在y轴上时,设,则,
∴点M不能在y轴上,
设,到AC的距离为h,如图:
则,,
当M位于AC左侧时,,得;
当M位于AC右侧时,,得;
综上所述:,.
26.(1)解:∵,∴,解得:,∴A(16,0),B(0,12);
(2)解:存在t,使得△OCP的面积等于△OCQ面积的2倍由(1)知,A(16,0),B(0,12),∴OA=16,OB=12,∵,∴,∵C(8,6),∴,,∵△OCP的面积等于△OCQ面积的2倍,∴ ,解得:,∴当时,△OCP的面积等于△OCQ面积的2倍;
(3)解:2∠GOB+∠BAE=∠OHA,理由如下:∵∠COA+∠BOC=∠BOA=90°,∴∠OBA+∠BAO=90°,又∵∠COA=∠CAO,∴∠OBA=∠BOC,∵y轴平分∠GOC,∴∠GOB=∠BOC,∴∠GOB=∠OBA,∴OG∥BA,过点H作HF∥OG交x轴于F,
∴HF∥BA,∴∠FHA=∠BAE,∵OG∥FH,∴∠GOC=∠FHO,∴∠GOC+∠BAE=∠FHO+∠FHA ,即∠GOC+∠BAE=∠OHA,∴2∠GOB+∠BAE=∠OHA.
一、单选题
1.对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(﹣a,b),如f(1,2)=(﹣1,2);g(a,b)=(b,a),如g(1,2)=(2,1),据此得g[f(5,﹣9)]=( )
A.(5,﹣9) B.(﹣5,﹣9) C.(﹣9,﹣5) D.(﹣9,5)
2.在平面直角坐标系中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为,点的坐标为( )
A. B. C. D.
3.已知点位于第二象限,并且,a,b均为整数,则满足条件的点A个数有( )
A.4个 B.5个 C.6个 D.7个
4.已知点E(x0,yo),点F(x2.y2),点M(x1,y1)是线段EF的中点,则x1=,y1=.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
A.(4,0) B.(﹣2,2) C.(2,﹣4) D.(﹣4,2)
5.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
6.如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
A.3 B.4 C.5 D.6
7.如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
A. ()2015 B. ()2016 C. ()2017 D. ()2018
8.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是( )
A.M(1,﹣3),N(﹣1,﹣3)
B.M(﹣1,﹣3),N(﹣1,3)
C.M(﹣1,﹣3),N(1,﹣3)
D.M(﹣1,3),N(1,﹣3)
9.如图,已知直线l1⊥l2,且在某平面直角坐标系中, x轴∥l1,y轴∥l2,若点A的坐标为(-1,2),点B的坐标为(2,-1),则点C在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,平面直角坐标系中,△ABC≌△DEF, AB=BC=5.若A点的坐标为(﹣3,1),B、C两点在直线y=﹣3上,D、E两点在y轴上,则点F的横坐标为( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在平面直角在坐标系中,四边形OACB的两边OA,OB分别在x轴、y轴的正半轴上,其中,且CO平分,若,,则点C的坐标为______.
12.如图,在平面直角坐标系中,点A(0,4)在y轴正半轴上,点B(-3,0)在x轴负半轴上,且AB=5,点M坐标为(3,0),N点为线段OA上一动点,P为线段AB上的一动点,则MN+NP的最小值为___________.
13.如图,平面直角坐标系中,A(﹣3,0)B(0,4)把△AOB按如图标记的方式连续做旋转变换,这样得到的第2017个三角形中,O点的对应点的坐标为_____.
14.如图,在平面直角坐标系中,点、点,点P是x轴正半轴上—动点,给出4个结论:
①线段AB的长为;
②在,若,则的面积是5;
③当时,点P的坐标为;
④设点P的坐标为,则的最小值为.
其中正确的结论有______.
15.如图,在平面直角坐标系中,点,点,将线段绕着点P逆时针旋转90°,得到线段,连接,,则的最小值为__________.
16.如图,在平面直角坐标系中,点,点是x轴上的一个动点.
(1)用含x的式子表示线段的长是_____;
(2)结合图形,判断式子的最小值是____.
17.如图,等腰是由三块面向内的镜面组成的,其中,边上靠近点的三等分点处发出一道光线,经镜面两次反射后恰好回到点,若,则光线走过的路径是______.
18.如图,点的坐标为,点的坐标为,分别以,为直角边在第三、第四象限作等腰,等腰,连接交轴于点,点的坐标是______.
19.如图,在平面直角坐标系中,是边长为的等边三角形,是边上的高,点是上的一个动点,若点的坐标是,则的最小值是________.
20.在平面直角坐标系中,点A(3,0),B(0,6),作△BOC,使△BOC与△ABO全等,则点C坐标为 _______________.
三、解答题
21.在平面直角坐标系中,点A的坐标为,过点作x轴的垂线l,点A与点B关于直线l对称;
(1) 点B的坐标为________;
(2) 点C的坐标为,顺次连接,若在四边形内部有一个点P,满足,且,求点P的坐标;
(3) 在四边形外部是否存在点Q,满足,且,若存在,直接写出Q点坐标,若不存在请说明理由.
22.如图,的顶点A,B分别在x轴,y轴上,;
(1) 若,且点B(0,2),C(-2,-1),
① 点C关于y轴对称点的坐标为______;
② 求点A的坐标;
(2) 若点B与原点重合,时,存在第三象限的点E和y轴上的点F,使,且A(3,0),C(0,m),F(0,n),线段EF的长度为,求AE的长.
23.对于平面内的及其内部的一点,设点到直线,的距离分别为,,称和这两个数中较大的一个为点关于的“偏率”在平面直角坐标系中,点,分别为轴正半轴,轴正半轴上的两个点.
(1) 若点的坐标为,则点关于的“偏率”为______;
(2) 若第一象限内点关于的“偏率”为1,则,满足的关系为______;
(3) 若第一象限内点关于的“偏率”为2.在平面直角坐标系上,画出所有点E形成的图形.
24.如图,在平面直角坐标系中,已知,,其中,满足,点为第三象限内一点.
(1)若到坐标轴的距离相等,,且,求点坐标
(2)若为,请用含的式子表示的面积.
(3)在(2)条件下,当时,在轴上有点,使得的面积是的面积的2倍,请求出点的坐标.
25.已知:在平面直角坐标系中,点在第四象限,且到x轴的距离为2,到y轴的距离为1.
(1) 求点的坐标;
(2) 若轴,且点C到x轴的距离与点A到x轴的距离相等,请直接写出点C的坐标;
(3) 在坐标轴上是否存在一点M,使的面积的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由.
26.如图,在平面直角坐标系中,点A、B的坐标分别为、,且实数a、b满足.
求A、B两点的坐标;
如图1,已知坐标轴上有两动点P,Q同时出发,P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动,点P到达O点整个运动随之结束.AB的中点C的坐标是,设运动时间为t秒.是否存在这样的t,使得的面积等于面积的2倍?若存在,请求出t的值;若不存在,请说明理由;
如图2,在(2)的条件下,若,点G是第二象限中一点,并且y轴平分.点E是线段OB上一动点,连接AE交OC于点H,当点E在线段OB上运动的过程中,探究,,之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
答案
一、单选题
1.C 2.D 3.B 4.B 5.B 6.D 7.B 8.C 9.C 10.C
二、填空题
11.
12.
13.(8064,0)
14.①②④
15.
16. 5
17.
18.
19.
20.或或
三、解答题
21.
解:(1)点A的坐标为,过点作x轴的垂线l,
到的距离为,
则
故答案为:
(2)如图,,,
点与点关于对称,
在四边形内部有一个点P,满足,
则点在上,设点,
,
即
解得或
在四边形内部
(3)存在,由(2)可知时,在四边形外部
故
22.(1)解:(1)①由关于y轴对称的点纵坐标不变、横坐标变为原来的相反数,则点C(-2,-1)关于y轴对称点的坐标为(2,-1);
故答案是(2,-1);
②设A点坐标为(a,0)
∵B(0,2),C(-2,-1),
∴BC=
∴AB=BC=
∴,解得a=3.
∴点A的坐标为(3,0).
(2)解:(2)作点F关于x轴的对称点H(0,-n),则AF=AH、OF=OH,过点H作HN⊥AC于点N,过点F作FM⊥AE于点M,
∵C(0,m),H(0,-n),m<0,n>0,
∴HC=OC-OH=-m-n,
∵EF=-m-n,
∴HC=EF,
∵∠AEF=∠ACO=30°,
∴∠FME=∠HNC,
∴△FEM≌△HCN(AAS),
∴FM=HN,EM=CN,
在Rt△AFM和Rt△AHN中,
AF=AH,FM=HN
∴Rt△AFM≌Rt△AHN(HL),
∴AM=AN,
∴EM+AM=CN+AN,
∴AE=AC,
∵∠ACO=30°,A(3,0),
∴OA=3,
∴AC=2OA=6,
∴AE=6.
23.
(1)解:∵点M,N分别在x轴正半轴,y轴正半轴上,
∴点P(1,5)到OM距离d1=5,到ON距离d2=1,
∴点P关于∠MON的“偏率”为:5;
故答案为:5;
(2)∵点Q(a,b)在第一象限,到OM距离d1=b,到ON距离d2=a,
∴点Q关于∠MON的“偏率”为:1或1,
∴a=b,
故答案为:a=b;
(3)∵点在第一象限,
∴点E到OM距离d1=y,到ON距离d2=x,
又∵点E关于的“偏率”为2,
∴点E关于∠MON的“偏率”为:2或,
即点E在函数或的图象上,
点E形成的图形如图所示:
24.解:(1)由题意可知:
,
求得,
∵,
∴,,
∴,,
∴,
∵,,
∴,
∵,
∴或者,
∴或;
(2)由题意可得:
,
∵在三象限,
∴,
∴;
(3)当时,,
由题意可得:
,
,
,
,
∴或.
25.(1)解:∵点在第四象限,且到x轴的距离为2,到y轴的距离为1,
∴,解得:,
∴,,
∴
(2)解:由(1)可知:,
∵轴,点C到x轴的距离与点A到x轴的距离相等,
∴C的横坐标为1,纵坐标为2,
∴
(3)解:假设存在点M,使得,
∵,,
∴,
∴,
当点M在y轴上时,设,则,
∴点M不能在y轴上,
设,到AC的距离为h,如图:
则,,
当M位于AC左侧时,,得;
当M位于AC右侧时,,得;
综上所述:,.
26.(1)解:∵,∴,解得:,∴A(16,0),B(0,12);
(2)解:存在t,使得△OCP的面积等于△OCQ面积的2倍由(1)知,A(16,0),B(0,12),∴OA=16,OB=12,∵,∴,∵C(8,6),∴,,∵△OCP的面积等于△OCQ面积的2倍,∴ ,解得:,∴当时,△OCP的面积等于△OCQ面积的2倍;
(3)解:2∠GOB+∠BAE=∠OHA,理由如下:∵∠COA+∠BOC=∠BOA=90°,∴∠OBA+∠BAO=90°,又∵∠COA=∠CAO,∴∠OBA=∠BOC,∵y轴平分∠GOC,∴∠GOB=∠BOC,∴∠GOB=∠OBA,∴OG∥BA,过点H作HF∥OG交x轴于F,
∴HF∥BA,∴∠FHA=∠BAE,∵OG∥FH,∴∠GOC=∠FHO,∴∠GOC+∠BAE=∠FHO+∠FHA ,即∠GOC+∠BAE=∠OHA,∴2∠GOB+∠BAE=∠OHA.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
