浙教版八年级数学上册试题 5.4一次函数的图象 (含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 5.4一次函数的图象 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 516.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 11:46:22 | ||
图片预览



文档简介
5.4一次函数的图象
一、单选题
1.若直线y=ax+b不经过第三象限,则下列不等式中,总成立的是 ( )
A.b﹥0 B.b-a﹤0 C.b-a﹥0 D.a+b﹥0
2.已知abc0,而且,那么直线y=px+p一定通过( ).
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
3.函数y=a|x|与y=x+a的图象恰有两个公共点,则实数a的取值范围是( )
A.a>1 B.-1<a<1 C.a>1或a<-1 D.a≥1或a≤-1
4.如图,点A,B,C在一次函数的图象上,它们的横坐标依次为-1,1,2,分别过这些点作轴与轴的垂线,则图中阴影部分的面积之和是( )
A.3 B.4.5 C. D.
5.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是( )
A. B.
C. D.且
6.把直线向上平移个单位后,与直线的交点在第二象限,则的取值范围是( )
A. B. C. D.
7.如图,一次函数的图象与直线交点的横坐标为5,则不等式
的解集为( )
A. B. C. D.
8.已知点,,,四点在直线的图象上,且,则的大小关系为( )
A. B. C. D.
9.如图,点A、B的坐标分别为、,点P为x轴上的动点,若点B关于直线AP的对称点恰好落在x轴上,则点P的坐标是( )
A. B. C. D.
10.如图,已知A(3,1)与B(1,0),PQ是直线上的一条动线段且(Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
A.(,) B.(,) C.(0,0) D.(1,1)
二、填空题
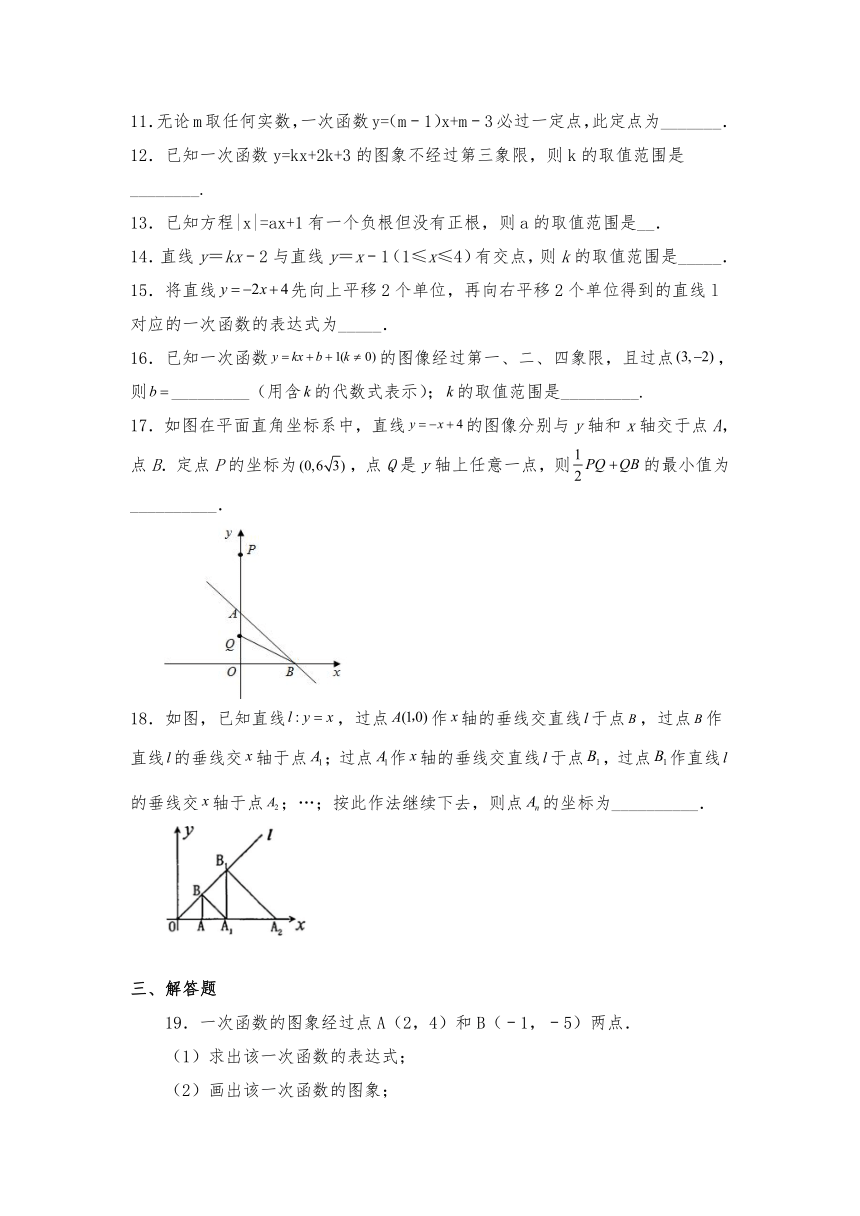
11.无论m取任何实数,一次函数y=(m﹣1)x+m﹣3必过一定点,此定点为_______.
12.已知一次函数y=kx+2k+3的图象不经过第三象限,则k的取值范围是________.
13.已知方程|x|=ax+1有一个负根但没有正根,则a的取值范围是__.
14.直线y=kx﹣2与直线y=x﹣1(1≤x≤4)有交点,则k的取值范围是_____.
15.将直线先向上平移2个单位,再向右平移2个单位得到的直线l对应的一次函数的表达式为_____.
16.已知一次函数的图像经过第一、二、四象限,且过点,则_________(用含的代数式表示);的取值范围是_________.
17.如图在平面直角坐标系中,直线的图像分别与y轴和x轴交于点A,点B.定点P的坐标为,点Q是y轴上任意一点,则的最小值为__________.
18.如图,已知直线,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;…;按此作法继续下去,则点的坐标为__________.
三、解答题
19.一次函数的图象经过点A(2,4)和B(﹣1,﹣5)两点.
(1)求出该一次函数的表达式;
(2)画出该一次函数的图象;
(3)判断(﹣5,﹣4)是否在这个函数的图象上?
(4)求出该函数图象与坐标轴围成的三角形面积.
20.已知一次函数.
(1)m为何值时,图象经过原点?
(2)将该一次函数向下平移3个单位长度后得到的函数图象经过点,求平移后的函数解析式.
21.已知一次函数.
(1)当时,这个函数的函数值随的增大而增大还是随的增大而减小呢?
(2)当这个函数的图象与直线平行时,求的值.
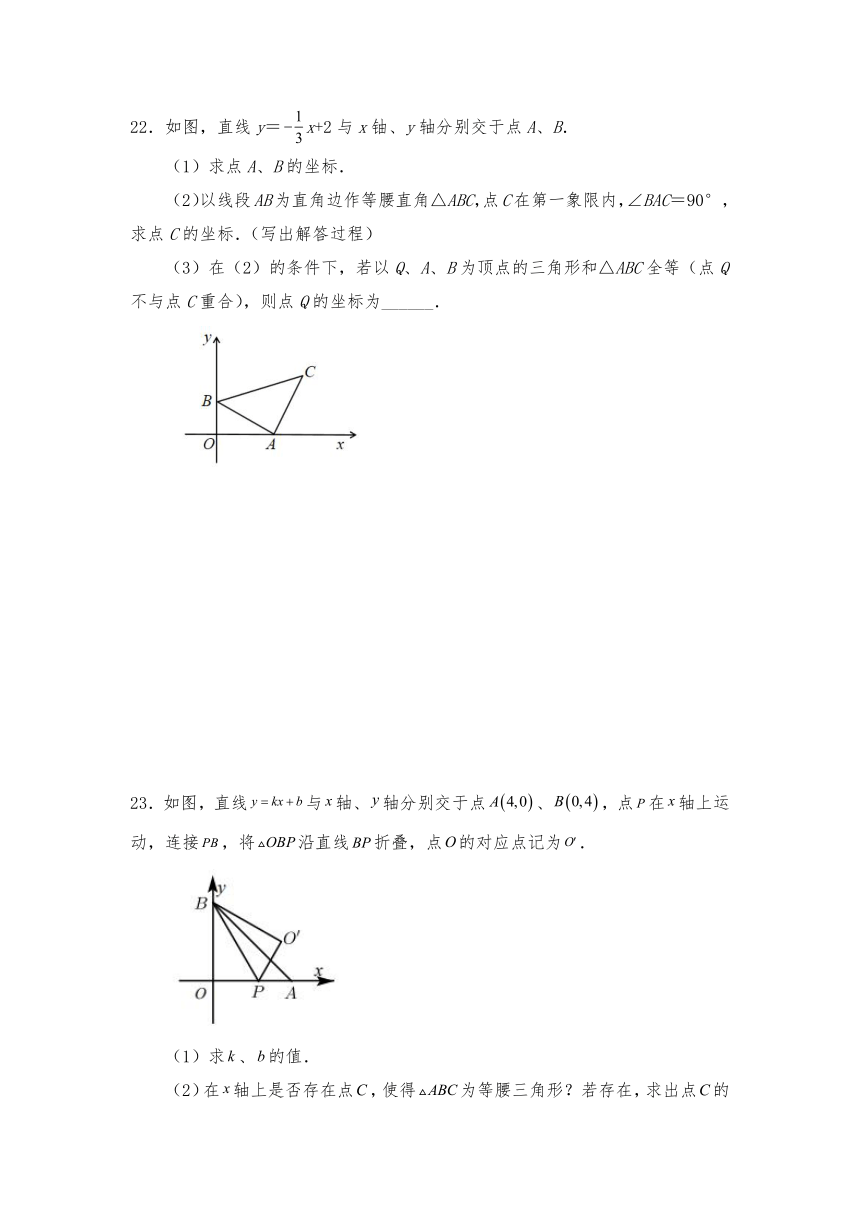
22.如图,直线y=x+2与x铀、y轴分别交于点A、B.
(1)求点A、B的坐标.
(2)以线段AB为直角边作等腰直角△ABC,点C在第一象限内,∠BAC=90°,求点C的坐标.(写出解答过程)
(3)在(2)的条件下,若以Q、A、B为顶点的三角形和△ABC全等(点Q不与点C重合),则点Q的坐标为______.
23.如图,直线与轴、轴分别交于点、,点在轴上运动,连接,将沿直线折叠,点的对应点记为.
(1)求、的值.
(2)在轴上是否存在点,使得为等腰三角形?若存在,求出点的坐标,若不存在,说明理由.
(3)若点恰好落在直线上,求的面积.
24.如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点.OA、OB的长度分别为m和n,且满足m2+n2=2mn.
(1)判断△AOB的形状.
(2)如图②,正比例函数y=kx(k<0)的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=13,MN=6,求BN的长.
(3)如图③,E为线段AB上一动点,以AE为斜边作等腰直角△ADE,P为BE的中点,连接PD、PO.试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明.
答案
一、单选题
1.C 2.B 3.C 4.B 5.D 6.A 7.B 8.B 9.A 10.A
二、填空题
11.(﹣1,﹣2).
12.≤k≤0
13.a>﹣1
14.≤k≤2
15.
16.
17.
18.
二、填空题
19.解:(1)设一次函数的解析式为y=kx+b
∵一次函数的图象经过点A(2,4)和B(﹣1,﹣5)两点
∴,
解得:
∴一次函数的表达式为y=3x﹣2;
(2)描出A、B点,作出一次函数的图象如图:
(3)由(1)知,一次函数的表达式为y=3x﹣2
将x=﹣5代入此函数表达式中得,y=3×(﹣5)﹣2=﹣17≠﹣4
∴(﹣5,﹣4)不在这个函数的图象上;
(4)由(1)知,一次函数的表达式为y=3x﹣2
令x=0,则y=﹣2,令y=0,则3x﹣2=0,
∴x=,
∴该函数图象与坐标轴围成的三角形面积为:×2×=.
20.
解:(1)∵一次函数的图象经过原点,
∴,
解得m=4;
(2)一次函数向下平移3个单位长度后得到的函数解析式为
∵该图象经过点(2,5),
∴,
解得m=2,
∴平移后的函数的解析式为y=5x-5.
21.
解:(1)∵,
∴,
∴一次函数y随着x的增大而增大;
(2)∵一次函数与直线平行,
∴,
∴.
22.
解:(1)直线y=x+2与x铀、y轴分别交于点A、B,
令 ,解得: ,则 ,
令 ,解得: ,则 ,
(2)过点C作CM⊥x轴,CN⊥y轴,
∵ ,
∴ ,
∵,
∴ ,
∵△ABC为等腰直角三角形, ,
∴ ,
∴ ,
∵,,
∴ ,
∴ ,
设c点坐标为 ,则 ,
∴ ;
(3)
①设Q点坐标为,
∵ ,
∴ ,
由(2)知,则 , ,
∴ ,
解得:,
∵点Q与点C不重合,
则.
②设Q点坐标为,当时,
∵,
∴ ,
∴ ,
解得: ,
∴,
综上,Q点坐标为或或.
23.
解:(1)将点,点的坐标代入得:
,
∴,.
(2)设,
①当时,,,,
当,即时,,,
∴
当,即时,,,
∴;
②当时,、两点关于原点对称,∴;
③当时.
∵,,∴为等腰直角三角形,
∴当时,、两点重合,∴,
综上所述:,,,.
如图,①当点在直线上时,
设,∴,,,
在中,,
,,
.
②当P在x轴的负半轴时,如图所示:
由折叠得:∠PO'B=∠POB=90°,O'B=OB=4,
∵∠BAO=45°,
∴PO'=PO=AO'=,
∴S△OBP=OB OP=×4×()=;
综上所述,△OBP的面积为或.
24.
解:(1)△AOB是等腰直角三角形,
理由:
∵m2+n2=2mn,
∴m2+n2﹣2mn=0,
∴(m﹣n)2=0,
∴m=n,即OA=OB,
∵∠AOB=90°,
∴△AOB为等腰直角三角形;
(2)∵AM⊥ON,BN⊥ON,
∴∠AMO=∠BNO=90°,
∴∠MOA+∠MAO=90°,
∵∠MOA+∠NOB=90°,
∴∠MAO=∠NOB,
在△MAO和△NOB中,
,
∴△MAO≌△NOB(AAS),
∴OM=BN,AM=ON=13,
∵MN=ON﹣OM,MN=6,
∴6=13﹣OM,
∴OM=7,
∴BN=7;
(3)PO=PD且PO⊥PD,
如图3,延长DP到点C,使PC=DP,连接CB、OD、OC,
在△DEP和△CBP,
,
∴△DEP≌△CBP(SAS),
∴CB=DE=DA,∠DEP=∠CBP=135°,
则∠CBO=∠CBP﹣∠ABO=135°﹣45°=90°,
又∵∠BAO=45°,∠DAE=45°,
∴∠DAO=90°,
在△OAD和△OBC,
,
∴△OAD≌△OBC(SAS),
∴OD=OC,∠AOD=∠COB,
∴∠DOC=∠AOB=90°,
∴△DOC为等腰直角三角形,
∵PC=DP,
∴PO=PD,PO⊥PD.
一、单选题
1.若直线y=ax+b不经过第三象限,则下列不等式中,总成立的是 ( )
A.b﹥0 B.b-a﹤0 C.b-a﹥0 D.a+b﹥0
2.已知abc0,而且,那么直线y=px+p一定通过( ).
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
3.函数y=a|x|与y=x+a的图象恰有两个公共点,则实数a的取值范围是( )
A.a>1 B.-1<a<1 C.a>1或a<-1 D.a≥1或a≤-1
4.如图,点A,B,C在一次函数的图象上,它们的横坐标依次为-1,1,2,分别过这些点作轴与轴的垂线,则图中阴影部分的面积之和是( )
A.3 B.4.5 C. D.
5.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线()与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是( )
A. B.
C. D.且
6.把直线向上平移个单位后,与直线的交点在第二象限,则的取值范围是( )
A. B. C. D.
7.如图,一次函数的图象与直线交点的横坐标为5,则不等式
的解集为( )
A. B. C. D.
8.已知点,,,四点在直线的图象上,且,则的大小关系为( )
A. B. C. D.
9.如图,点A、B的坐标分别为、,点P为x轴上的动点,若点B关于直线AP的对称点恰好落在x轴上,则点P的坐标是( )
A. B. C. D.
10.如图,已知A(3,1)与B(1,0),PQ是直线上的一条动线段且(Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
A.(,) B.(,) C.(0,0) D.(1,1)
二、填空题
11.无论m取任何实数,一次函数y=(m﹣1)x+m﹣3必过一定点,此定点为_______.
12.已知一次函数y=kx+2k+3的图象不经过第三象限,则k的取值范围是________.
13.已知方程|x|=ax+1有一个负根但没有正根,则a的取值范围是__.
14.直线y=kx﹣2与直线y=x﹣1(1≤x≤4)有交点,则k的取值范围是_____.
15.将直线先向上平移2个单位,再向右平移2个单位得到的直线l对应的一次函数的表达式为_____.
16.已知一次函数的图像经过第一、二、四象限,且过点,则_________(用含的代数式表示);的取值范围是_________.
17.如图在平面直角坐标系中,直线的图像分别与y轴和x轴交于点A,点B.定点P的坐标为,点Q是y轴上任意一点,则的最小值为__________.
18.如图,已知直线,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;…;按此作法继续下去,则点的坐标为__________.
三、解答题
19.一次函数的图象经过点A(2,4)和B(﹣1,﹣5)两点.
(1)求出该一次函数的表达式;
(2)画出该一次函数的图象;
(3)判断(﹣5,﹣4)是否在这个函数的图象上?
(4)求出该函数图象与坐标轴围成的三角形面积.
20.已知一次函数.
(1)m为何值时,图象经过原点?
(2)将该一次函数向下平移3个单位长度后得到的函数图象经过点,求平移后的函数解析式.
21.已知一次函数.
(1)当时,这个函数的函数值随的增大而增大还是随的增大而减小呢?
(2)当这个函数的图象与直线平行时,求的值.
22.如图,直线y=x+2与x铀、y轴分别交于点A、B.
(1)求点A、B的坐标.
(2)以线段AB为直角边作等腰直角△ABC,点C在第一象限内,∠BAC=90°,求点C的坐标.(写出解答过程)
(3)在(2)的条件下,若以Q、A、B为顶点的三角形和△ABC全等(点Q不与点C重合),则点Q的坐标为______.
23.如图,直线与轴、轴分别交于点、,点在轴上运动,连接,将沿直线折叠,点的对应点记为.
(1)求、的值.
(2)在轴上是否存在点,使得为等腰三角形?若存在,求出点的坐标,若不存在,说明理由.
(3)若点恰好落在直线上,求的面积.
24.如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点.OA、OB的长度分别为m和n,且满足m2+n2=2mn.
(1)判断△AOB的形状.
(2)如图②,正比例函数y=kx(k<0)的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=13,MN=6,求BN的长.
(3)如图③,E为线段AB上一动点,以AE为斜边作等腰直角△ADE,P为BE的中点,连接PD、PO.试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明.
答案
一、单选题
1.C 2.B 3.C 4.B 5.D 6.A 7.B 8.B 9.A 10.A
二、填空题
11.(﹣1,﹣2).
12.≤k≤0
13.a>﹣1
14.≤k≤2
15.
16.
17.
18.
二、填空题
19.解:(1)设一次函数的解析式为y=kx+b
∵一次函数的图象经过点A(2,4)和B(﹣1,﹣5)两点
∴,
解得:
∴一次函数的表达式为y=3x﹣2;
(2)描出A、B点,作出一次函数的图象如图:
(3)由(1)知,一次函数的表达式为y=3x﹣2
将x=﹣5代入此函数表达式中得,y=3×(﹣5)﹣2=﹣17≠﹣4
∴(﹣5,﹣4)不在这个函数的图象上;
(4)由(1)知,一次函数的表达式为y=3x﹣2
令x=0,则y=﹣2,令y=0,则3x﹣2=0,
∴x=,
∴该函数图象与坐标轴围成的三角形面积为:×2×=.
20.
解:(1)∵一次函数的图象经过原点,
∴,
解得m=4;
(2)一次函数向下平移3个单位长度后得到的函数解析式为
∵该图象经过点(2,5),
∴,
解得m=2,
∴平移后的函数的解析式为y=5x-5.
21.
解:(1)∵,
∴,
∴一次函数y随着x的增大而增大;
(2)∵一次函数与直线平行,
∴,
∴.
22.
解:(1)直线y=x+2与x铀、y轴分别交于点A、B,
令 ,解得: ,则 ,
令 ,解得: ,则 ,
(2)过点C作CM⊥x轴,CN⊥y轴,
∵ ,
∴ ,
∵,
∴ ,
∵△ABC为等腰直角三角形, ,
∴ ,
∴ ,
∵,,
∴ ,
∴ ,
设c点坐标为 ,则 ,
∴ ;
(3)
①设Q点坐标为,
∵ ,
∴ ,
由(2)知,则 , ,
∴ ,
解得:,
∵点Q与点C不重合,
则.
②设Q点坐标为,当时,
∵,
∴ ,
∴ ,
解得: ,
∴,
综上,Q点坐标为或或.
23.
解:(1)将点,点的坐标代入得:
,
∴,.
(2)设,
①当时,,,,
当,即时,,,
∴
当,即时,,,
∴;
②当时,、两点关于原点对称,∴;
③当时.
∵,,∴为等腰直角三角形,
∴当时,、两点重合,∴,
综上所述:,,,.
如图,①当点在直线上时,
设,∴,,,
在中,,
,,
.
②当P在x轴的负半轴时,如图所示:
由折叠得:∠PO'B=∠POB=90°,O'B=OB=4,
∵∠BAO=45°,
∴PO'=PO=AO'=,
∴S△OBP=OB OP=×4×()=;
综上所述,△OBP的面积为或.
24.
解:(1)△AOB是等腰直角三角形,
理由:
∵m2+n2=2mn,
∴m2+n2﹣2mn=0,
∴(m﹣n)2=0,
∴m=n,即OA=OB,
∵∠AOB=90°,
∴△AOB为等腰直角三角形;
(2)∵AM⊥ON,BN⊥ON,
∴∠AMO=∠BNO=90°,
∴∠MOA+∠MAO=90°,
∵∠MOA+∠NOB=90°,
∴∠MAO=∠NOB,
在△MAO和△NOB中,
,
∴△MAO≌△NOB(AAS),
∴OM=BN,AM=ON=13,
∵MN=ON﹣OM,MN=6,
∴6=13﹣OM,
∴OM=7,
∴BN=7;
(3)PO=PD且PO⊥PD,
如图3,延长DP到点C,使PC=DP,连接CB、OD、OC,
在△DEP和△CBP,
,
∴△DEP≌△CBP(SAS),
∴CB=DE=DA,∠DEP=∠CBP=135°,
则∠CBO=∠CBP﹣∠ABO=135°﹣45°=90°,
又∵∠BAO=45°,∠DAE=45°,
∴∠DAO=90°,
在△OAD和△OBC,
,
∴△OAD≌△OBC(SAS),
∴OD=OC,∠AOD=∠COB,
∴∠DOC=∠AOB=90°,
∴△DOC为等腰直角三角形,
∵PC=DP,
∴PO=PD,PO⊥PD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
