浙教版八年级数学上册 第1章 三角形的初步知识 单元复习题(含答案)
文档属性
| 名称 | 浙教版八年级数学上册 第1章 三角形的初步知识 单元复习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 812.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 11:49:24 | ||
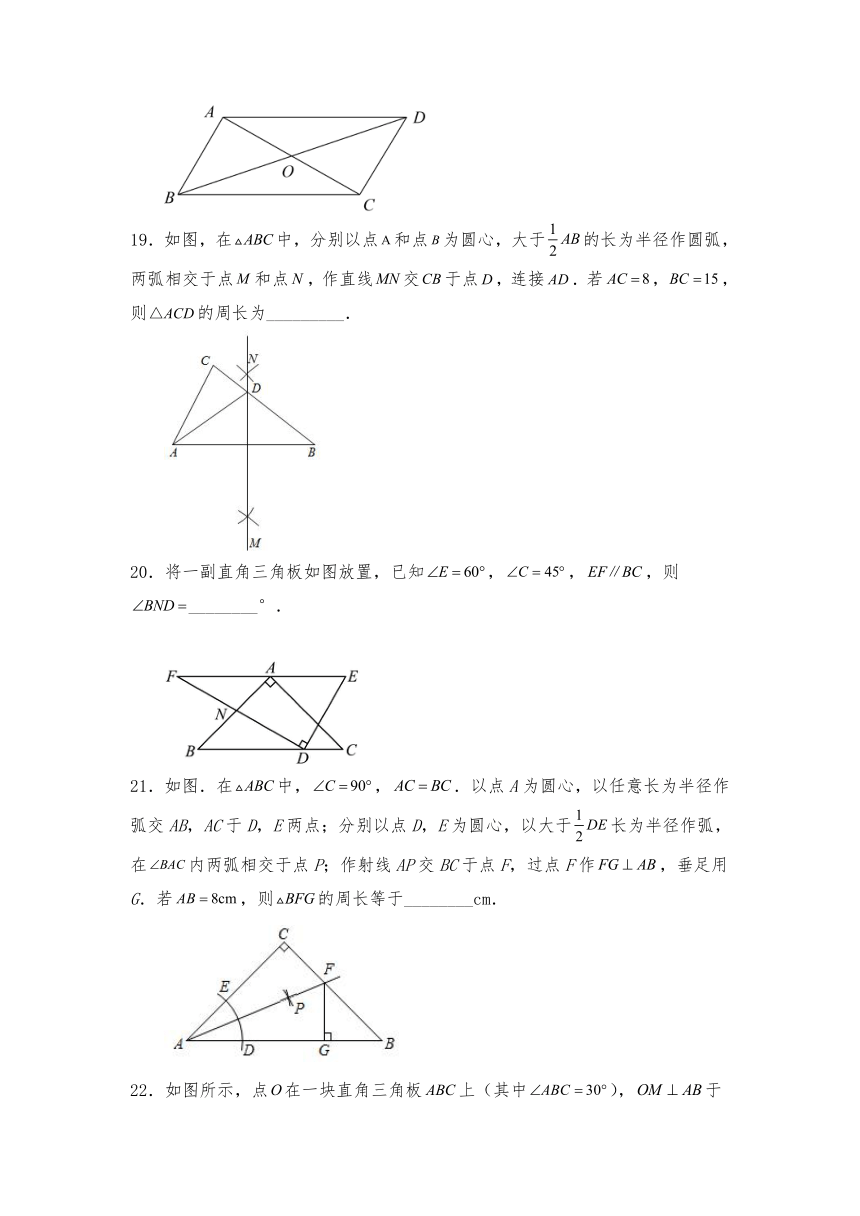
图片预览




文档简介
《三角形的初步知识》单元复习题
一、单选题
1.下列多边形具有稳定性的是( )
A. B. C. D.
2.下列长度的三条线段能首尾相接构成三角形的是( )
A.,, B.,,
C.,, D.,,
3.如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
4.下列四个图形中,线段BE是△ABC的高的是( )
A. B.
C. D.
5.在中,若一个内角等于另外两个角的差,则( )
A.必有一个角等于 B.必有一个角等于
C.必有一个角等于 D.必有一个角等于
6.锐角三角形的三个内角是∠A、∠B、∠C,如果,,,那么、、这三个角中 ( )
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
7.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A.中线 B.中位线 C.高线 D.角平分线
8.八一中学校九年级2班学生杨冲家和李锐家到学校的直线距离分别是和.那么杨冲,李锐两家的直线距离不可能是( )
A. B. C. D.
9.下列命题中,是真命题的有( )
①对角线相等且互相平分的四边形是矩形 ②对角线互相垂直的四边形是菱形
③四边相等的四边形是正方形 ④四边相等的四边形是菱形
A.①② B.①④ C.②③ D.③④
10.如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
11.如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使DOEFOE,你认为要添加的那个条件是( )
A.OD=OE B.OE=OF C.∠ODE =∠OED D.∠ODE=∠OFE
12.如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A. B. C. D.
13.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
14.如图,在和中,点,,,在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
15.如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A.25 B.22 C.19 D.18
二、填空题
16.如图,在中,平分若则____.
17.如图,在中,是中线的中点.若的面积是1,则的面积是______.
18.如图,在四边形ABCD中,对角线AC,BD相交于点O,,请你添加一个条件________,使.
19.如图,在中,分别以点和点为圆心,大于的长为半径作圆弧,两弧相交于点和点,作直线交于点,连接.若,,则的周长为_________.
将一副直角三角板如图放置,已知,,,则________°.
21.如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于________cm.
22.如图所示,点在一块直角三角板上(其中),于点,于点,若,则_________度.
三、解答题
23.已知:,.
求作:点P,使点P在内部,且.
24.如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
25.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求的大小.
26.如图,AC平分,垂足分别为B,D.
(1)求证:;
(2)若,求四边形ABCD的面积.
27.已知:如图,点A、D、C、F在同一直线上,,,.
求证:.
如图,点D是△ABC外一点,连接BD、 AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC= BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.
已知: ,
求证:
答案
一、单选题
1.D 2.B 3.D 4.D 5.D 6.A 7.D
8.A 9.B 10.B 11.D 12.C 13.C 14.B 15.C
二、填空题
16.1
17.2
18.OB=OD(答案不唯一)
19.23
20.105
21.8
22.15
三、解答题
23.
解:如图,点P即为所求:
24.
解:如图,射线即为所求作.
25.
解:∵,
∴,
∴,
∴在和中,
∴,
∴.
26.
解:(1) AC平分,
,
,
;
(2),,
,
,
,
四边形ABCD的面积.
27.
证明:∵,
∴,
在与中,
,
∴,
∴,
∴,
∴.
28.
解:已知:BC=AD,∠ABC=∠BAD,
求证:AC=BD.
证明:在△ABC和△BAD中,
∵,
∴,
∴,
即命题得证.
一、单选题
1.下列多边形具有稳定性的是( )
A. B. C. D.
2.下列长度的三条线段能首尾相接构成三角形的是( )
A.,, B.,,
C.,, D.,,
3.如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
4.下列四个图形中,线段BE是△ABC的高的是( )
A. B.
C. D.
5.在中,若一个内角等于另外两个角的差,则( )
A.必有一个角等于 B.必有一个角等于
C.必有一个角等于 D.必有一个角等于
6.锐角三角形的三个内角是∠A、∠B、∠C,如果,,,那么、、这三个角中 ( )
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
7.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A.中线 B.中位线 C.高线 D.角平分线
8.八一中学校九年级2班学生杨冲家和李锐家到学校的直线距离分别是和.那么杨冲,李锐两家的直线距离不可能是( )
A. B. C. D.
9.下列命题中,是真命题的有( )
①对角线相等且互相平分的四边形是矩形 ②对角线互相垂直的四边形是菱形
③四边相等的四边形是正方形 ④四边相等的四边形是菱形
A.①② B.①④ C.②③ D.③④
10.如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
11.如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使DOEFOE,你认为要添加的那个条件是( )
A.OD=OE B.OE=OF C.∠ODE =∠OED D.∠ODE=∠OFE
12.如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A. B. C. D.
13.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
14.如图,在和中,点,,,在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
15.如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点,.作直线,交于点,交于点,连接.若,,,则的周长为( )
A.25 B.22 C.19 D.18
二、填空题
16.如图,在中,平分若则____.
17.如图,在中,是中线的中点.若的面积是1,则的面积是______.
18.如图,在四边形ABCD中,对角线AC,BD相交于点O,,请你添加一个条件________,使.
19.如图,在中,分别以点和点为圆心,大于的长为半径作圆弧,两弧相交于点和点,作直线交于点,连接.若,,则的周长为_________.
将一副直角三角板如图放置,已知,,,则________°.
21.如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于________cm.
22.如图所示,点在一块直角三角板上(其中),于点,于点,若,则_________度.
三、解答题
23.已知:,.
求作:点P,使点P在内部,且.
24.如图,已知是的一个外角.请用尺规作图法,求作射线,使.(保留作图痕迹,不写作法)
25.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求的大小.
26.如图,AC平分,垂足分别为B,D.
(1)求证:;
(2)若,求四边形ABCD的面积.
27.已知:如图,点A、D、C、F在同一直线上,,,.
求证:.
如图,点D是△ABC外一点,连接BD、 AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC= BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.
已知: ,
求证:
答案
一、单选题
1.D 2.B 3.D 4.D 5.D 6.A 7.D
8.A 9.B 10.B 11.D 12.C 13.C 14.B 15.C
二、填空题
16.1
17.2
18.OB=OD(答案不唯一)
19.23
20.105
21.8
22.15
三、解答题
23.
解:如图,点P即为所求:
24.
解:如图,射线即为所求作.
25.
解:∵,
∴,
∴,
∴在和中,
∴,
∴.
26.
解:(1) AC平分,
,
,
;
(2),,
,
,
,
四边形ABCD的面积.
27.
证明:∵,
∴,
在与中,
,
∴,
∴,
∴,
∴.
28.
解:已知:BC=AD,∠ABC=∠BAD,
求证:AC=BD.
证明:在△ABC和△BAD中,
∵,
∴,
∴,
即命题得证.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
