浙教版八年级数学上册试题 2.4 等腰三角形的性质与判定同步测试(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 2.4 等腰三角形的性质与判定同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 770.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 11:56:45 | ||
图片预览




文档简介
2.4 等腰三角形的性质与判定
一、单选题
1.等腰三角形的一个外角等于130°,则它的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
2.已知a,b是等腰三角形的两边长,且a,b满足,则此等腰三角形的周长为( )
A.8 B.6或8 C.7 D.7或8
3.如图,△ABC中,AB=AC,AD是BC边上的中线.按下列步骤作图:①分别以点A、C为圆心,大于的长为半径作弧,相交于M、N两点;②直线MN交AD于点E;③连接EB.下列结论中错误的是( )
A.AD⊥BC B.EA=EB C.∠AEB=2∠ACB D.∠EBD=2∠EBA
4.如图,在△ABC中,小美同学按以下步骤作图:①以点C为圆心,以BC的长为半径画弧,交AC于点D,连接BD;②分别以点B,D为圆心,以大于BD的长为半径画弧,两弧交于点E;③作射线CE交BD于点F,连接AF.若△ABC的面积为10,则△ACF的面积为( )
A.2.5 B.5 C.7.5 D.8
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,过AB的中点E作FE⊥AB,垂足为E.下列说法正确的有( )个
①AF=BF;②AD⊥BC;③BF⊥AC;④若AB=10,BD=4,则△BCF的周长为18
A.1 B.2 C.3 D.4
6.如图,已知直线,将等边三角形如图放置.若,则等于( )
A.17° B.22° C.27° D.32°
7.如图,过边长为4的等边三角形的边AB上一点P,作于点E,Q为BC延长线上一点,当时,连接PQ交边AC于点D,则DE的长为( )
A.2 B.3 C.4 D.
8.如图,是正三角形(等边三角形),D、E分别是边BC、AC上的两点,且,AD与BE相交于点P,则下列结论正确的是( )
①;②;③;④
A.①②③④ B.①②③ C.①③④ D.①②④
9.△ABC为等边三角形,点E为边AB的中点,点Q为边BC上一动点,以EQ为边作等边△EQF(点F在EQ的右侧),连接AF、FC,点P在射线CB上,且满足PE=EQ,有以下四个结论①∠FQC=∠QEB;②FQ=FC;③PB+QC=AE;④当AF⊥AB时,BC=4PB,其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,△ABC 中,AC=DC=3,BD 垂直∠BAC 的角平分线于 D,E 为 AC 的中点,则图中两个阴影部分面积之差的最大值为( )
A.6 B.4.5 C.3 D.2
二、填空题
11.等腰三角形的周长为,若有一边长为,则等腰三角形的其他两边长分别是____________.
12.如图,中,H是高的交点,且,则_____________.
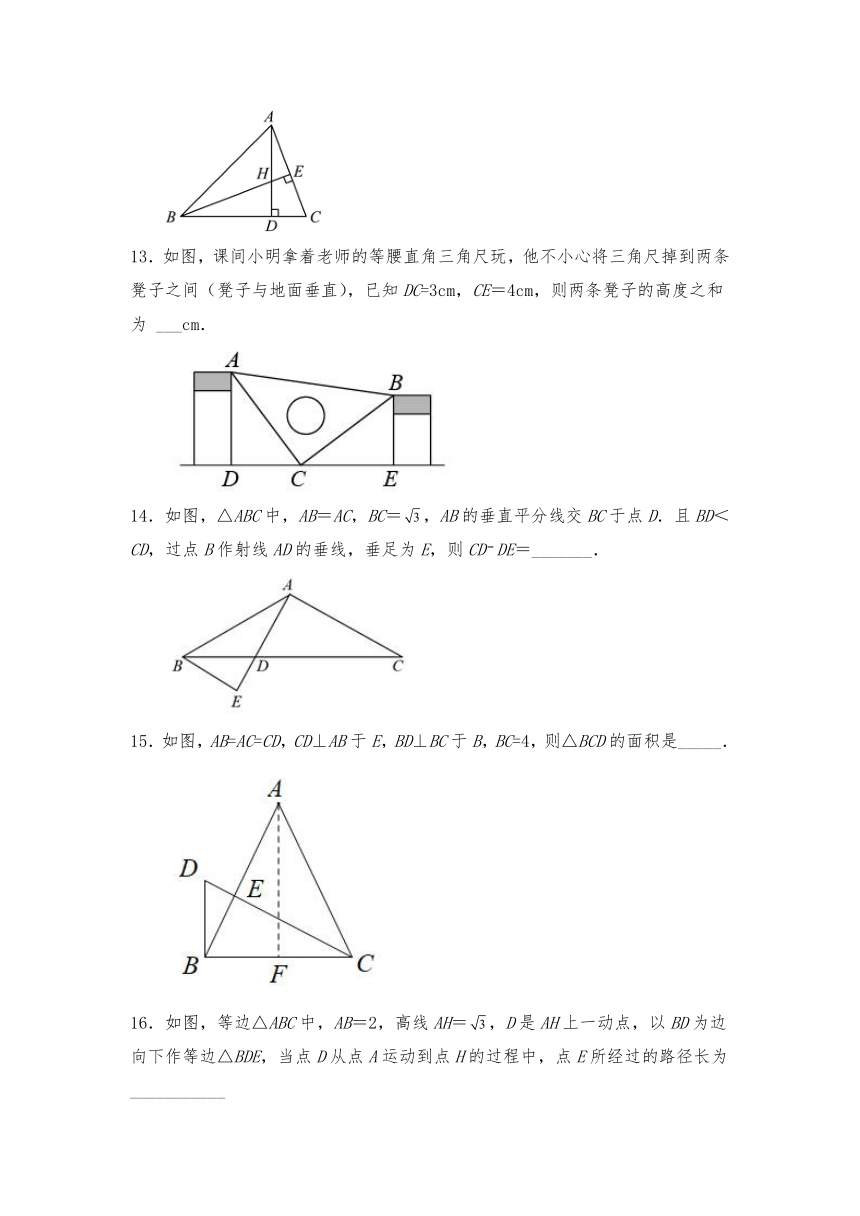
13.如图,课间小明拿着老师的等腰直角三角尺玩,他不小心将三角尺掉到两条凳子之间(凳子与地面垂直),已知DC=3cm,CE=4cm,则两条凳子的高度之和为 ___cm.
14.如图,△ABC中,AB=AC,BC=,AB的垂直平分线交BC于点D.且BD<CD,过点B作射线AD的垂线,垂足为E,则CDDE=_______.
15.如图,AB=AC=CD,CD⊥AB于E,BD⊥BC于B,BC=4,则△BCD的面积是_____.
16.如图,等边△ABC中,AB=2,高线AH=,D是AH上一动点,以BD为边向下作等边△BDE,当点D从点A运动到点H的过程中,点E所经过的路径长为___________
17.如图,在△ABC中,AB=AC=10,BC=16,AD=6,AD是∠BAC的角平分线.若E,F分别是AD和AC上的动点,则EC+EF的最小值是________.
18.如图,中,E是线段上一点,,,于D,,四边形的面积为8,则的面积为________.
三、解答题
19.阅读下列分解因式的过程:
.这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:;
(2)三边,,满足,判断的形状
20.如图,△ABC中,AB=AC,∠BAC=45°,AD⊥BC,CE⊥AB.求证:
△AEF≌△CEB; (2) AF=2CD.
21.如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD; (2)求∠BFD的度数.
22.已知,在中,,,点为直线上一动点(点不与点,重合),连接,以为边作,使,,且点和点分别在直线的异侧,连接.
(1) 如图1,当点在线段上时,求的度数;
(2) 若,,请直接写出的长.
23.如图1,点C在线段AB上,点D,E分别在AB的上方和下方,且,,______.
(1)请你从①,②中选择一个合适的条件填入上述横线中,使得(只填序号),并给出证明;
(2)在(1)的条件下,连接DE,作平分交DE于点F,如图2,试判断CF与DE的位置关系,并给出证明.
24.如图1,在等边中,D、E分别为边BC、AC上任意一点,连接AD、BE,AD与BE相交于点O,且.
请直接写出线段AD与BE之间的数量关系:______________;______________.
【推广探究】如图2,在等边中,P、M分别为边AB、AC上的点,且,过点P作交AC于点O,过点M作交BC于点N,PQ与MN交于点F.
(1)______________.
(2)求证:.
【深入探究】如图3,在“推广探究”的条件下,令四边形APFN的周长为,四边形CNFQ的周长为,,则______________(请用含有a、b的代数式表示).
答案
一、单选题
1.C 2.D 3.D 4.B 5.C
6.B 7.A 8.C 9.C 10.B
二、填空题
11.9cm、1cm或5cm、5cm.
12.45°
13.7
14.
15.4
16.
17.
18.6
三、解答题
19.
(1)解:
(2)∵,
∴,
∴,
∴,
∴或,
即:或,
∴是等腰三角形.
20.
(1)证明:∵∠BAC=45°,CE⊥AB,
∴∠BAC=∠ACE=45°,
∴AE=CE,
∵AD⊥BC,
∴∠B+∠BAD=90°=∠B+∠BCE,
∴∠BAD=∠BCE,
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)证明:∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC,
∴BC=2CD,
∴AF=2CD.
21.
(1)证明:∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°.
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS),
(2)解:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠BAD+∠CAD=60°,
∴∠BAD+∠EBA=60°,
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=60°.
22.
(1)解:∵∠BAC=∠DAE=90°,
∴∠BAC ∠DAC=∠DAE ∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴∠ABC=∠ACE=45°,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∴∠ECB=∠ACB+∠ACE=45°+45°=90°;
(2)解:当点D在线段BC上时,
∵BC=5,CD=2,
∴BD=BC CD=3,
由(1)得△ABD≌△ACE,
∴BD=CE,
∴CE=3,
当点D在线段BC的延长线上时,如图,
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵BC=5,CD=2,
∴BD=BC+CD=7,
∴CE=7,
综上,CE长为3或7.
23.
(1)选择②.
证明:∵,
∴,
在和中,
∵,
∴;
(2).
证明:∵,
∴,
∵CF平分,
∴.
24.
解:如图1,
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,AD=BE,
∴∠AOE=∠OBA+∠BAD=∠OBA+∠CBE=∠CBA=60°,
故答案为:AD=BE,60;
【推广探究】
(1)∵PQ∥BE,MN∥AD,
∴∠QMF=∠EAO,∠MQF=∠AEO,
在△MQF中,∠MFQ+∠QMF+MQF=180°,
在△AEO中,∠AOE+∠EAO+∠AEO=180°,
∴∠MFQ=∠AOE=60°,
故答案为:60;
(2)∵∠APQ+∠PAQ+∠PQA=180°,
∠MFQ+∠MQF+∠FMQ=180°,
且∠PAQ=∠MFQ=60°,
∴∠APQ=∠FMQ,
∵AM=BP,
∴AP=CM,
在△PAQ和△MCN中,
,
∴△PAQ≌△MCN(ASA),
∴PQ=MN;
【深入探究】
∵AM=BP,CQ=BN,
∴AP+AM=CQ+CN,
∵PQ=MN,
∴PF+b=a+c,
∴PF=a+c-b,
∴a+PF-b-c=a+a+c-b-b-c=2a-2b,
故答案为:2a-2b.
一、单选题
1.等腰三角形的一个外角等于130°,则它的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
2.已知a,b是等腰三角形的两边长,且a,b满足,则此等腰三角形的周长为( )
A.8 B.6或8 C.7 D.7或8
3.如图,△ABC中,AB=AC,AD是BC边上的中线.按下列步骤作图:①分别以点A、C为圆心,大于的长为半径作弧,相交于M、N两点;②直线MN交AD于点E;③连接EB.下列结论中错误的是( )
A.AD⊥BC B.EA=EB C.∠AEB=2∠ACB D.∠EBD=2∠EBA
4.如图,在△ABC中,小美同学按以下步骤作图:①以点C为圆心,以BC的长为半径画弧,交AC于点D,连接BD;②分别以点B,D为圆心,以大于BD的长为半径画弧,两弧交于点E;③作射线CE交BD于点F,连接AF.若△ABC的面积为10,则△ACF的面积为( )
A.2.5 B.5 C.7.5 D.8
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,过AB的中点E作FE⊥AB,垂足为E.下列说法正确的有( )个
①AF=BF;②AD⊥BC;③BF⊥AC;④若AB=10,BD=4,则△BCF的周长为18
A.1 B.2 C.3 D.4
6.如图,已知直线,将等边三角形如图放置.若,则等于( )
A.17° B.22° C.27° D.32°
7.如图,过边长为4的等边三角形的边AB上一点P,作于点E,Q为BC延长线上一点,当时,连接PQ交边AC于点D,则DE的长为( )
A.2 B.3 C.4 D.
8.如图,是正三角形(等边三角形),D、E分别是边BC、AC上的两点,且,AD与BE相交于点P,则下列结论正确的是( )
①;②;③;④
A.①②③④ B.①②③ C.①③④ D.①②④
9.△ABC为等边三角形,点E为边AB的中点,点Q为边BC上一动点,以EQ为边作等边△EQF(点F在EQ的右侧),连接AF、FC,点P在射线CB上,且满足PE=EQ,有以下四个结论①∠FQC=∠QEB;②FQ=FC;③PB+QC=AE;④当AF⊥AB时,BC=4PB,其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,△ABC 中,AC=DC=3,BD 垂直∠BAC 的角平分线于 D,E 为 AC 的中点,则图中两个阴影部分面积之差的最大值为( )
A.6 B.4.5 C.3 D.2
二、填空题
11.等腰三角形的周长为,若有一边长为,则等腰三角形的其他两边长分别是____________.
12.如图,中,H是高的交点,且,则_____________.
13.如图,课间小明拿着老师的等腰直角三角尺玩,他不小心将三角尺掉到两条凳子之间(凳子与地面垂直),已知DC=3cm,CE=4cm,则两条凳子的高度之和为 ___cm.
14.如图,△ABC中,AB=AC,BC=,AB的垂直平分线交BC于点D.且BD<CD,过点B作射线AD的垂线,垂足为E,则CDDE=_______.
15.如图,AB=AC=CD,CD⊥AB于E,BD⊥BC于B,BC=4,则△BCD的面积是_____.
16.如图,等边△ABC中,AB=2,高线AH=,D是AH上一动点,以BD为边向下作等边△BDE,当点D从点A运动到点H的过程中,点E所经过的路径长为___________
17.如图,在△ABC中,AB=AC=10,BC=16,AD=6,AD是∠BAC的角平分线.若E,F分别是AD和AC上的动点,则EC+EF的最小值是________.
18.如图,中,E是线段上一点,,,于D,,四边形的面积为8,则的面积为________.
三、解答题
19.阅读下列分解因式的过程:
.这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:;
(2)三边,,满足,判断的形状
20.如图,△ABC中,AB=AC,∠BAC=45°,AD⊥BC,CE⊥AB.求证:
△AEF≌△CEB; (2) AF=2CD.
21.如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD; (2)求∠BFD的度数.
22.已知,在中,,,点为直线上一动点(点不与点,重合),连接,以为边作,使,,且点和点分别在直线的异侧,连接.
(1) 如图1,当点在线段上时,求的度数;
(2) 若,,请直接写出的长.
23.如图1,点C在线段AB上,点D,E分别在AB的上方和下方,且,,______.
(1)请你从①,②中选择一个合适的条件填入上述横线中,使得(只填序号),并给出证明;
(2)在(1)的条件下,连接DE,作平分交DE于点F,如图2,试判断CF与DE的位置关系,并给出证明.
24.如图1,在等边中,D、E分别为边BC、AC上任意一点,连接AD、BE,AD与BE相交于点O,且.
请直接写出线段AD与BE之间的数量关系:______________;______________.
【推广探究】如图2,在等边中,P、M分别为边AB、AC上的点,且,过点P作交AC于点O,过点M作交BC于点N,PQ与MN交于点F.
(1)______________.
(2)求证:.
【深入探究】如图3,在“推广探究”的条件下,令四边形APFN的周长为,四边形CNFQ的周长为,,则______________(请用含有a、b的代数式表示).
答案
一、单选题
1.C 2.D 3.D 4.B 5.C
6.B 7.A 8.C 9.C 10.B
二、填空题
11.9cm、1cm或5cm、5cm.
12.45°
13.7
14.
15.4
16.
17.
18.6
三、解答题
19.
(1)解:
(2)∵,
∴,
∴,
∴,
∴或,
即:或,
∴是等腰三角形.
20.
(1)证明:∵∠BAC=45°,CE⊥AB,
∴∠BAC=∠ACE=45°,
∴AE=CE,
∵AD⊥BC,
∴∠B+∠BAD=90°=∠B+∠BCE,
∴∠BAD=∠BCE,
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)证明:∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC,
∴BC=2CD,
∴AF=2CD.
21.
(1)证明:∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°.
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS),
(2)解:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠BAD+∠CAD=60°,
∴∠BAD+∠EBA=60°,
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=60°.
22.
(1)解:∵∠BAC=∠DAE=90°,
∴∠BAC ∠DAC=∠DAE ∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴∠ABC=∠ACE=45°,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∴∠ECB=∠ACB+∠ACE=45°+45°=90°;
(2)解:当点D在线段BC上时,
∵BC=5,CD=2,
∴BD=BC CD=3,
由(1)得△ABD≌△ACE,
∴BD=CE,
∴CE=3,
当点D在线段BC的延长线上时,如图,
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵BC=5,CD=2,
∴BD=BC+CD=7,
∴CE=7,
综上,CE长为3或7.
23.
(1)选择②.
证明:∵,
∴,
在和中,
∵,
∴;
(2).
证明:∵,
∴,
∵CF平分,
∴.
24.
解:如图1,
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,AD=BE,
∴∠AOE=∠OBA+∠BAD=∠OBA+∠CBE=∠CBA=60°,
故答案为:AD=BE,60;
【推广探究】
(1)∵PQ∥BE,MN∥AD,
∴∠QMF=∠EAO,∠MQF=∠AEO,
在△MQF中,∠MFQ+∠QMF+MQF=180°,
在△AEO中,∠AOE+∠EAO+∠AEO=180°,
∴∠MFQ=∠AOE=60°,
故答案为:60;
(2)∵∠APQ+∠PAQ+∠PQA=180°,
∠MFQ+∠MQF+∠FMQ=180°,
且∠PAQ=∠MFQ=60°,
∴∠APQ=∠FMQ,
∵AM=BP,
∴AP=CM,
在△PAQ和△MCN中,
,
∴△PAQ≌△MCN(ASA),
∴PQ=MN;
【深入探究】
∵AM=BP,CQ=BN,
∴AP+AM=CQ+CN,
∵PQ=MN,
∴PF+b=a+c,
∴PF=a+c-b,
∴a+PF-b-c=a+a+c-b-b-c=2a-2b,
故答案为:2a-2b.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
