浙教版八年级数学上册试题 2.6直角三角形同步测试(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 2.6直角三角形同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 442.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览


文档简介
2.6直角三角形
一、单选题
1.在Rt△ABC中,=90°,CD是AB边上的中线.且CD=5,则AB的长是( )
A.20 B.10 C.5 D.2.5
2.直角三角形的一锐角是50°,那么另一锐角是( )
A.40° B.50° C.60° D.70°
3.在如图所示的纸片中,,D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若,,则等于( )
A. B. C. D.
4.如图,在Rt△ABC中,,,于点D,E是AB的中点,若,则AB的长为( )
A.10 B.8 C.6 D.4
5.如图,在中,CD是斜边AB上的中线,若,则的度数为( )
A.26° B.48° C.52° D.64°
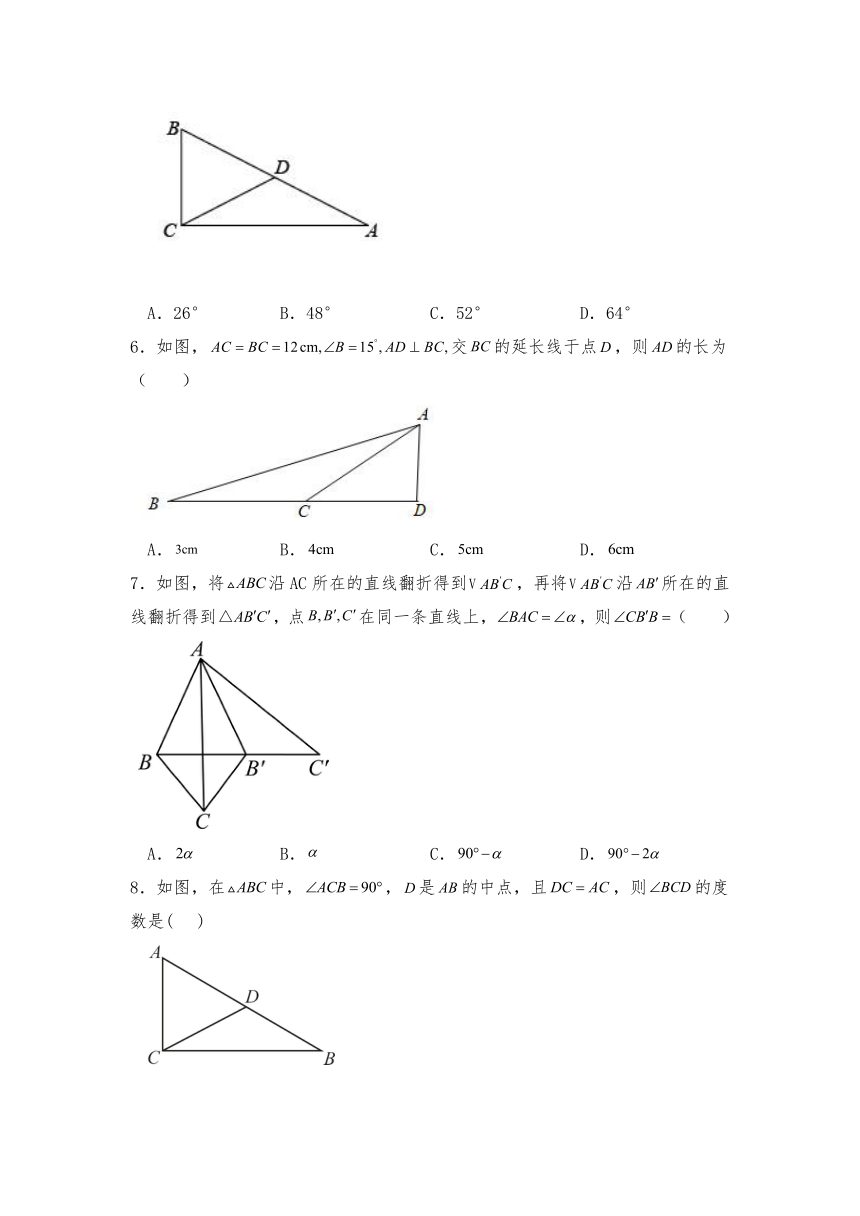
6.如图,交的延长线于点,则的长为( )
A. B. C. D.
7.如图,将沿AC所在的直线翻折得到,再将沿所在的直线翻折得到,点在同一条直线上,,则( )
A. B. C. D.
8.如图,在中,,是的中点,且,则的度数是( )
A.25° B.30° C.45° D.60°
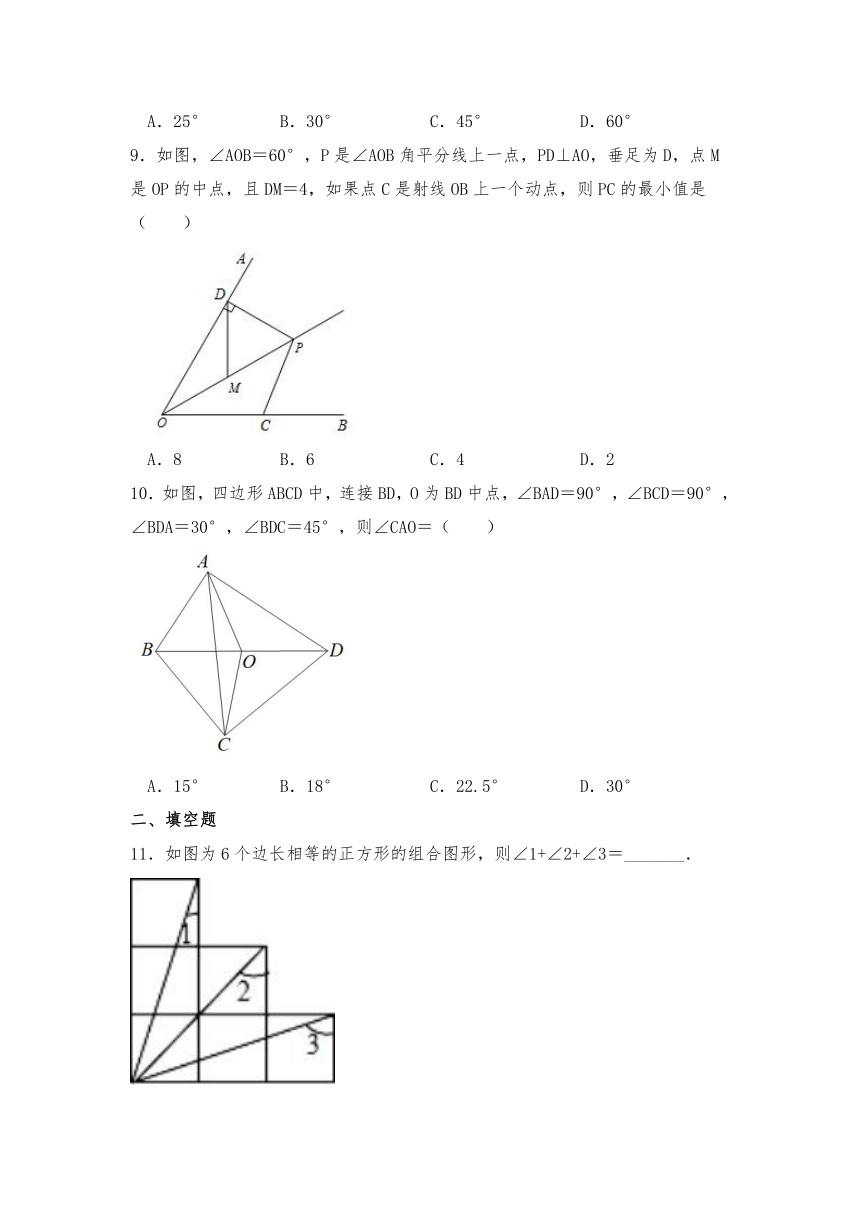
如图,∠AOB=60°,P是∠AOB角平分线上一点,PD⊥AO,垂足为D,点M是OP的中点,且DM=4,如果点C是射线OB上一个动点,则PC的最小值是( )
A.8 B.6 C.4 D.2
10.如图,四边形ABCD中,连接BD,O为BD中点,∠BAD=90°,∠BCD=90°,∠BDA=30°,∠BDC=45°,则∠CAO=( )
A.15° B.18° C.22.5° D.30°
二、填空题
11.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=_______.
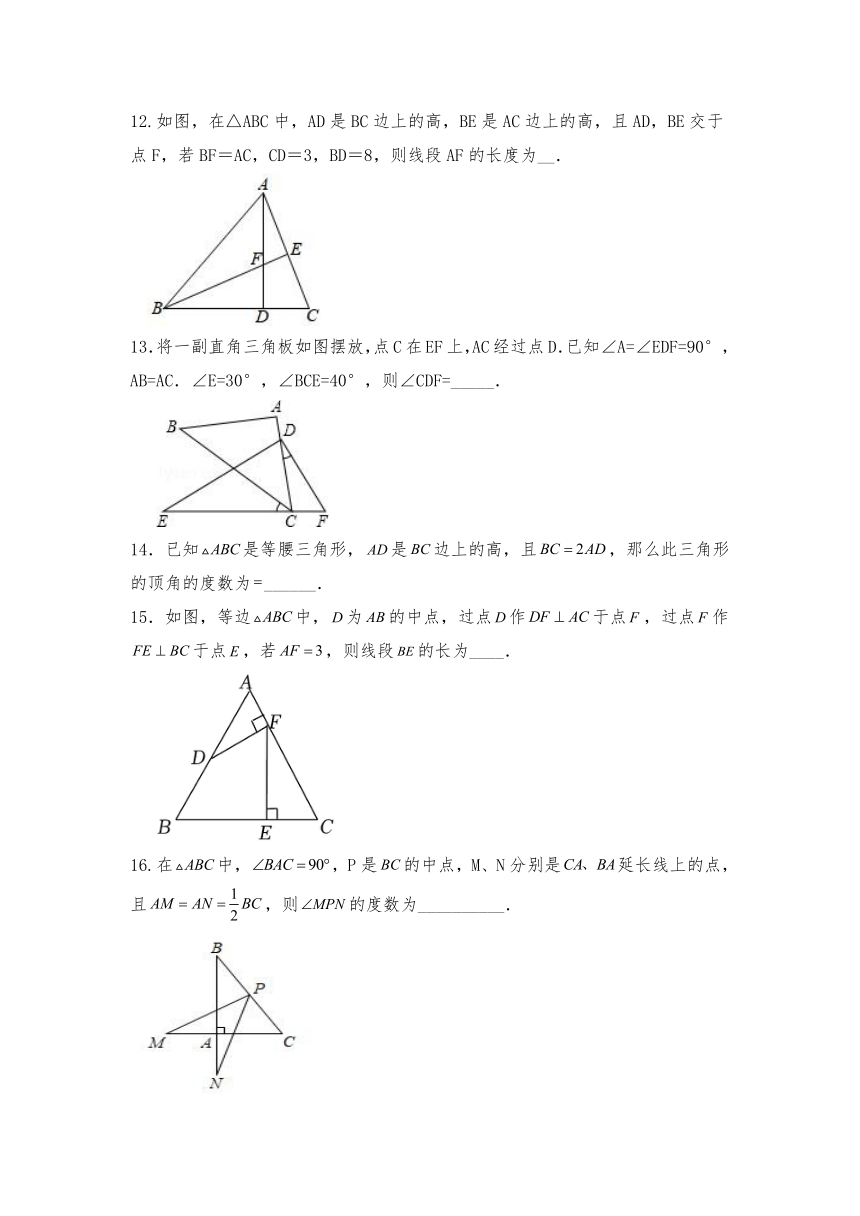
12.如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD,BE交于点F,若BF=AC,CD=3,BD=8,则线段AF的长度为__.
13.将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=_____.
14.已知是等腰三角形,是边上的高,且,那么此三角形的顶角的度数为______.
15.如图,等边中,为的中点,过点作于点,过点作于点,若,则线段的长为____.
16.在中,,P是的中点,M、N分别是延长线上的点,且,则的度数为__________.
如图,在锐角△ABC中,BC=4,∠ABC=30°,∠ABD=15°,直线BD交边AC于点D,点P、Q分别在线段BD、BC上运动,则PQ+PC的最小值是__________.
18.如图,在中,,,D为的中点,于N,交的延长线于点M,连接.则下列结论:①;②;③;④.其中正确的有______(填写序号即可)
三、解答题
19.如图,在中,是的平分线,,垂足为D,求证:.
20.如图,AC,BD为四边形ABCD的对角线,∠ABC=90°,∠ABD+∠ADB=∠ACB,∠ADC=∠BCD.
(1)求证:AD⊥AC;
(2)探求∠BAC与∠ACD之间的数量关系,并说明理由.
21.如图,中,,,的角平分线交于于点,点为上一点,且,,交于点.
(1)求的度数;
(2)若,求的长度
(3)若于点,证明:
22.如图,、分别是的两条高,点、点分别是、的中点.
(1) 求证:;
(2) 若,,求.
23.已知:如图,∠ACB=∠ADB=90°,M、N分别是AB、CD的中点.
求证:MD=MC,MN⊥CD.
如图,在中,,,的垂直平分线分别交和于点,,连接.
(1) 求证:是等边三角形:
(2) 若,求的长.
答案
一、单选题
1.B 2.A 3.B 4.A 5.C 6.D 7.A 8.B 9.C 10.A
二、填空题
11.135°
12.5
13.25°
14.或者
15.7.5
17.
18.①②③④
三、解答题
19.
【详解】证明:是的平分线,
,
由三角形的外角性质得,,
,
,
∴,
,
,
.
20.(1)∵在中,
在中,
,即
;
(2),理由如下:
由题(1)知,
.
21.(1)∵,
∴
又∵
∴
∵平分
∴
∴
(2)∵
∴BE=2CE=2
∵
∴AE=BE=2
∴AC=3
∴AD=AC=3
(3)∵CH⊥BE
∴
∵
∴HM=HC
∵ ,
∴
∵
∴
∴
22.
证明:如图,连接DM,DN.
∵BN、CM分别是△ABC的两条高,
∴BN⊥AC,CM⊥AB,
∴∠BMC=∠CNB=90°,
∵D是BC的中点,
∴DM=BC,DN=BC,
∴DM=DN,
∵E为MN的中点,
∴DE⊥MN;
(2)
解:∵Rt△BMC中,BC=5,D是BC的中点,
∴DM=2.5,
∵点E是MN的中点,MN=3,
∴ME=1.5,
由勾股定理得:DE=.
23.证明:∵∠ACB=∠ADB=90°,M是AB的中点,
∴,,
∴,
∵N是CD的中点,
∴.
24.
(1)
证:∵DE垂直平分AB,
∴D是AB的中点,
∵∠ACB=90°,∠A=30°,
∴∠B=60°,,
∴△BCD是等边三角形;
(2)
解:∵△BCD是等边三角形,
∴∠BCD=∠BDC=60°,
∴∠DCA=30°,
∵DE垂直平分AB,
∴∠ADE=∠BDE=90°,
∴∠CDE=30°=∠DCE,
∴CE=DE=1.
一、单选题
1.在Rt△ABC中,=90°,CD是AB边上的中线.且CD=5,则AB的长是( )
A.20 B.10 C.5 D.2.5
2.直角三角形的一锐角是50°,那么另一锐角是( )
A.40° B.50° C.60° D.70°
3.在如图所示的纸片中,,D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若,,则等于( )
A. B. C. D.
4.如图,在Rt△ABC中,,,于点D,E是AB的中点,若,则AB的长为( )
A.10 B.8 C.6 D.4
5.如图,在中,CD是斜边AB上的中线,若,则的度数为( )
A.26° B.48° C.52° D.64°
6.如图,交的延长线于点,则的长为( )
A. B. C. D.
7.如图,将沿AC所在的直线翻折得到,再将沿所在的直线翻折得到,点在同一条直线上,,则( )
A. B. C. D.
8.如图,在中,,是的中点,且,则的度数是( )
A.25° B.30° C.45° D.60°
如图,∠AOB=60°,P是∠AOB角平分线上一点,PD⊥AO,垂足为D,点M是OP的中点,且DM=4,如果点C是射线OB上一个动点,则PC的最小值是( )
A.8 B.6 C.4 D.2
10.如图,四边形ABCD中,连接BD,O为BD中点,∠BAD=90°,∠BCD=90°,∠BDA=30°,∠BDC=45°,则∠CAO=( )
A.15° B.18° C.22.5° D.30°
二、填空题
11.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=_______.
12.如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD,BE交于点F,若BF=AC,CD=3,BD=8,则线段AF的长度为__.
13.将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=_____.
14.已知是等腰三角形,是边上的高,且,那么此三角形的顶角的度数为______.
15.如图,等边中,为的中点,过点作于点,过点作于点,若,则线段的长为____.
16.在中,,P是的中点,M、N分别是延长线上的点,且,则的度数为__________.
如图,在锐角△ABC中,BC=4,∠ABC=30°,∠ABD=15°,直线BD交边AC于点D,点P、Q分别在线段BD、BC上运动,则PQ+PC的最小值是__________.
18.如图,在中,,,D为的中点,于N,交的延长线于点M,连接.则下列结论:①;②;③;④.其中正确的有______(填写序号即可)
三、解答题
19.如图,在中,是的平分线,,垂足为D,求证:.
20.如图,AC,BD为四边形ABCD的对角线,∠ABC=90°,∠ABD+∠ADB=∠ACB,∠ADC=∠BCD.
(1)求证:AD⊥AC;
(2)探求∠BAC与∠ACD之间的数量关系,并说明理由.
21.如图,中,,,的角平分线交于于点,点为上一点,且,,交于点.
(1)求的度数;
(2)若,求的长度
(3)若于点,证明:
22.如图,、分别是的两条高,点、点分别是、的中点.
(1) 求证:;
(2) 若,,求.
23.已知:如图,∠ACB=∠ADB=90°,M、N分别是AB、CD的中点.
求证:MD=MC,MN⊥CD.
如图,在中,,,的垂直平分线分别交和于点,,连接.
(1) 求证:是等边三角形:
(2) 若,求的长.
答案
一、单选题
1.B 2.A 3.B 4.A 5.C 6.D 7.A 8.B 9.C 10.A
二、填空题
11.135°
12.5
13.25°
14.或者
15.7.5
17.
18.①②③④
三、解答题
19.
【详解】证明:是的平分线,
,
由三角形的外角性质得,,
,
,
∴,
,
,
.
20.(1)∵在中,
在中,
,即
;
(2),理由如下:
由题(1)知,
.
21.(1)∵,
∴
又∵
∴
∵平分
∴
∴
(2)∵
∴BE=2CE=2
∵
∴AE=BE=2
∴AC=3
∴AD=AC=3
(3)∵CH⊥BE
∴
∵
∴HM=HC
∵ ,
∴
∵
∴
∴
22.
证明:如图,连接DM,DN.
∵BN、CM分别是△ABC的两条高,
∴BN⊥AC,CM⊥AB,
∴∠BMC=∠CNB=90°,
∵D是BC的中点,
∴DM=BC,DN=BC,
∴DM=DN,
∵E为MN的中点,
∴DE⊥MN;
(2)
解:∵Rt△BMC中,BC=5,D是BC的中点,
∴DM=2.5,
∵点E是MN的中点,MN=3,
∴ME=1.5,
由勾股定理得:DE=.
23.证明:∵∠ACB=∠ADB=90°,M是AB的中点,
∴,,
∴,
∵N是CD的中点,
∴.
24.
(1)
证:∵DE垂直平分AB,
∴D是AB的中点,
∵∠ACB=90°,∠A=30°,
∴∠B=60°,,
∴△BCD是等边三角形;
(2)
解:∵△BCD是等边三角形,
∴∠BCD=∠BDC=60°,
∴∠DCA=30°,
∵DE垂直平分AB,
∴∠ADE=∠BDE=90°,
∴∠CDE=30°=∠DCE,
∴CE=DE=1.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
