浙教版八年级数学上册试题 4.3.3 平面直角坐标系 折叠问题(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 4.3.3 平面直角坐标系 折叠问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 746.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 12:12:45 | ||
图片预览


文档简介
4.3.3 平面直角坐标系-折叠问题
一、单选题
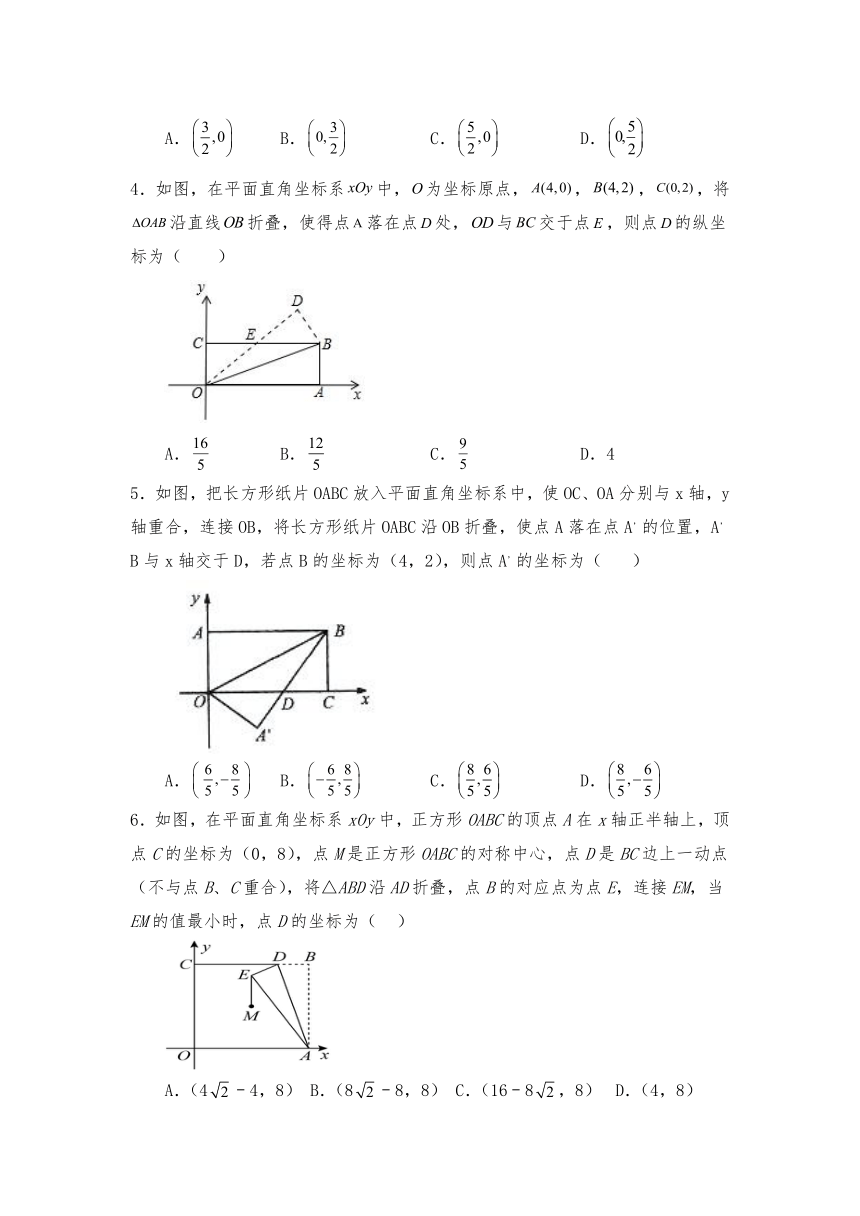
1.如图,在平面直角坐标系中,已知点A(2,1),B(3,﹣1),将线段AB沿y轴折叠,使点B落在点B1(﹣3,﹣1)处,则点A的对应点A1坐标为( )
A.(1,﹣2) B.(﹣2,1) C.(﹣1,﹣2) D.(﹣2,﹣1)
2.如图,在平面直角坐标系中,A(0,3),B(5,3),C(5,0),点D在线段OA上,将△ABD沿着直线BD折叠,点A的对应点为E,当点E在线段OC上时,则AD的长是( )
A.1 B. C. D.2
3.如图,在平面直角坐标系中,点A的坐标是,点B的坐标是,点C是OB上一点,将沿AC折叠,点B恰好落在x轴上的点处,则点C的坐标为( )
B. C. D.
4.如图,在平面直角坐标系中,为坐标原点,,,,将沿直线折叠,使得点落在点处,与交于点,则点的纵坐标为( )
A. B. C. D.4
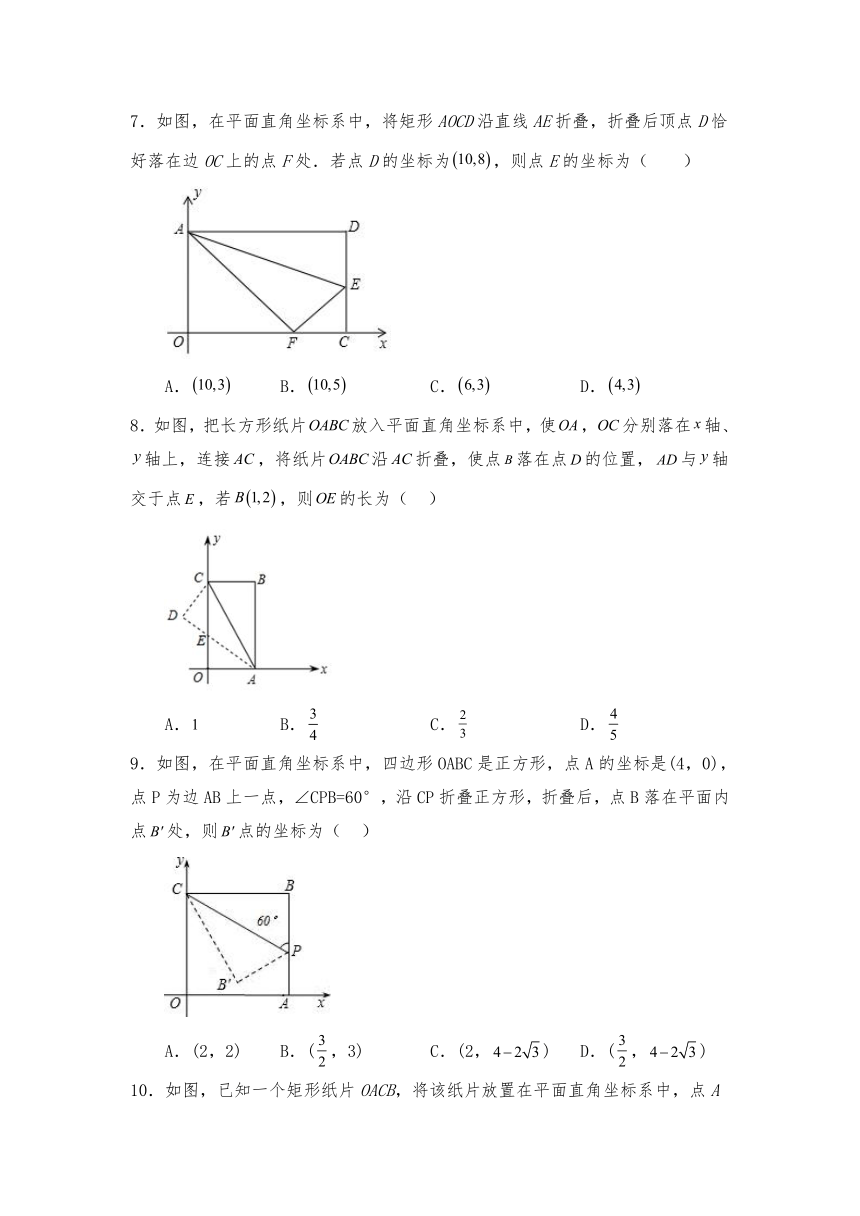
5.如图,把长方形纸片OABC放入平面直角坐标系中,使OC、OA分别与x轴,y轴重合,连接OB,将长方形纸片OABC沿OB折叠,使点A落在点A,的位置,A,B与x轴交于D,若点B的坐标为(4,2),则点A,的坐标为( )
A. B. C. D.
6.如图,在平面直角坐标系xOy中,正方形OABC的顶点A在x轴正半轴上,顶点C的坐标为(0,8),点M是正方形OABC的对称中心,点D是BC边上一动点(不与点B、C重合),将△ABD沿AD折叠,点B的对应点为点E,连接EM,当EM的值最小时,点D的坐标为( )
A.(4﹣4,8) B.(8﹣8,8) C.(16﹣8,8) D.(4,8)
7.如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠,折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为,则点E的坐标为( )
A. B. C. D.
8.如图,把长方形纸片放入平面直角坐标系中,使,分别落在轴、轴上,连接,将纸片沿折叠,使点落在点的位置,与轴交于点,若,则的长为( )
A. B. C. D.
9.如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点处,则点的坐标为( )
A.(2,2) B.(,3) C.(2,) D.(,)
10.如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为2﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在平面直角坐标系中,将矩形沿直线折叠(点E在边上),折叠后顶点D恰好落在边上的点F处,若点D的坐标为,则点E的坐标为____________.
12.如图,在平面直角坐标系中,长方形ABCD的边CO,OA分别在x轴、y轴上,点E在边BC上,将该长方形沿AE折叠,点B恰好落在边OC上的F处.若,,则点E的坐标是______.
如图,长方形OACB在平面直角坐标系中,O是坐标原点,点A,B分别在x轴与y轴上,已知OA=8,OB=10.把长方形沿OP折叠,点B的对应点B1恰好落在AC边上,则点P的坐标是________.
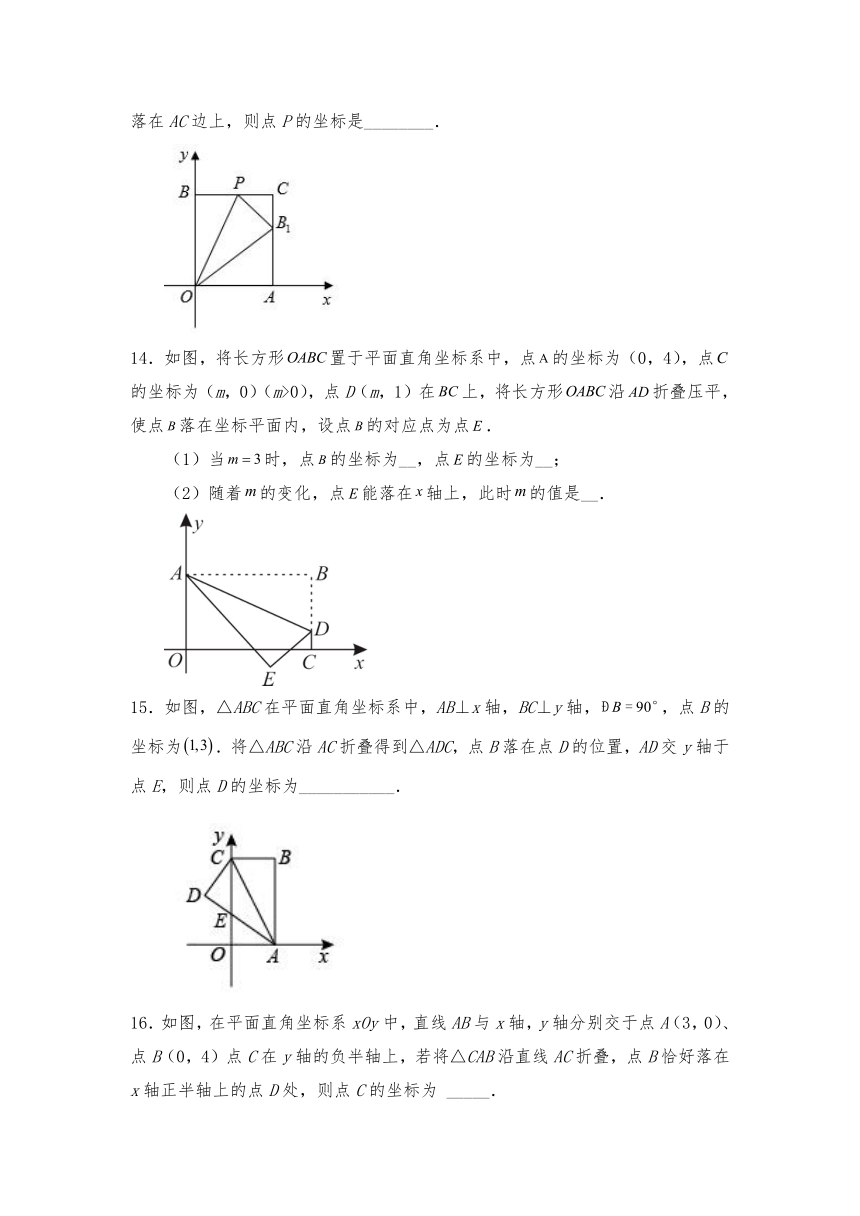
14.如图,将长方形置于平面直角坐标系中,点的坐标为(0,4),点的坐标为(m,0)(m>0),点D(m,1)在上,将长方形沿折叠压平,使点落在坐标平面内,设点的对应点为点.
(1)当时,点的坐标为__,点的坐标为__;
(2)随着的变化,点能落在轴上,此时的值是__.
15.如图,△ABC在平面直角坐标系中,AB⊥x轴,BC⊥y轴,,点B的坐标为.将△ABC沿AC折叠得到△ADC,点B落在点D的位置,AD交y轴于点E,则点D的坐标为___________.
16.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4)点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处,则点C的坐标为 _____.
17.如图,在平面直角坐标系中,已知点A(0,8),B(﹣6,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为 ___.
18.如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(2,4),则OE的长为___________.
19.如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴的负半轴、y轴的正半轴上,点D在边BC上,将该矩形沿AD折叠,点B恰好落在边OC上的E处,且△CDE为等腰直角三角形,若OA=4,则点D的坐标是_____.
20.如图所示,在平面直角坐标系中,点A的坐标为,点B在x的正半轴上,且,点E为的中点,连接,将沿折叠得到,其中交于点F,则点P的坐标是 ___________;点F的坐标是 ___________.
21.把一个矩形纸片如图放置在平面直角坐标系中,点A坐标为,点C坐,点D,E分别在边上,连接,将矩形沿着折叠后,点A落在点处,点O与点B重合,回答下面的问题:
(1)线段与相等吗?___________;
(2)点E的坐标为________________;
(3)折痕的长为_____________.
三、解答题
22.如图,在平面直角坐标系中,已知点,,连接.将沿过点的直线折叠,使点落在轴上的点处,折痕所在的直线交轴正半轴于点,求点的坐标.
23.如图,平面直角坐标系中有一个长方形OABC,OA在x轴上,OC在⊙O上,B的坐标为(8,6),将△ABC沿OB折叠,使点A与点D重合,OD与BC交于点E.
求证:△OCE≌△BDE;
求点E的坐标.
在矩形中,,,点D为边上一点,将沿直线
折叠,使点B恰好落在边上的点E处,分别以,所在的直线为x轴,y轴建立平面直角坐标系,求点D的坐标.
25.如图,长方形纸片ABCD放置在平面直角坐标系中,A与原点O重合.B、D分别在x轴和y轴上,,.
直接写出C点坐标;
如图①折叠使B落在线段AC的处,折痕为CE,求E点坐标;
如图②点P在线段DC上,若为等腰三角形,试求满足条件的所有P点坐标.
26.如图,将一张矩形纸片ABCD放入平面直角坐标系中,A(0,0),B(8,0),D(0,6),P为AD边上一点,将△ABP沿BP翻折,折叠后点A的对应点为A′.
如图①,当折叠后点A的对应点A′正好落在边DC上时,求A′C的长和A′的坐标;
如图②,当点P与点D重合时,点A的对应点为A′,A′B与DC相交于点E,求点E的坐标;
如图③,若沿BP翻折后PA′与CD相交于点E,恰好EA′=ED,BA'与CD相交于点F,求点P的坐标.(直接写出答案)
27.【问题初现】
(1)如图1,矩形OABC顶点O坐落在平面直角坐标系的原点上,C点的坐标为,,D是BC边上的点,且D的坐标是,求线段BD的长.
【问题延伸】
(2)在(1)的情况下,F为AB边上的一点,将沿直线DF折叠,若B点刚好落在x轴上的E点处,求E点的坐标.
【问题拓展】
(3)如图2,将上述情况变更为任意矩形,设B点坐标为、D点坐标为,在折叠过程中,折痕所在直线DF与y轴交于点G,当时,试判断线段OE与CD之间的数量关系,并给出证明.
答案
一、单选题
1.B 2.C 3.B 4.A 5.D 6.C 7.A 8.B 9.C 10.D
二、填空题
11.(5,)
12.
13.(5,10).
14. (3,4) (0,1)
15.
16.(0,-6)
17.
18.
19.(﹣4,).
20.
21. 相等
三、解答题
22.
解:连接交BC延长线于D,
由折叠可知,,,
,,
∴,
,
,
,
设,则,
在中,由勾股定理得,
∴,
解得,
,
故答案为:.
23.
解:(1)∵四边形OCBA为矩形,
∴CO=AB,∠OAB=∠OCE.
由翻折的性质可知∠D=∠OAB,BD=AB,
∴OC=BD,∠D=∠OCE.
∴在△OCE和△BDE中,∠D=∠OCE,∠CEO=∠DEB,OC=BD,
∴△OCE≌△BDE.
(2)∵△OCE≌△BDE,
∴EO=EB.
设CE=x,则.
在Rt△OCE中,OC=6,根据勾股定理得,,
∴,,
∴x=,
∴E(,6).
24.
解:∵矩形中,,,
∴,
∵将沿直线折叠,
∴,
在Rt△COE中
∴
设AD=m,则DE=BD=8-m,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,
即,解得m=3,
∴D(-3,-10).
25.解:(1)∵四边形ABCD是矩形,
∴CD=AB=8,BC=AD=6,
∴;
(2)在中,
∵折叠使B落在线段AC的B处,
∴,
∴
∴
∴
即
解得:
∴;
(3)如图,若为等腰三角形,
①当,即点P在AB的垂直平分线上,
∴;
②当
∴
∴;
③当BA=BP=8,即
∴
∴
∴;
综上所述,若为等腰三角形,P点坐标为:.
26.(1)解:(1)∵A(0,0),B(8,0),D(0,6),
∴AD=6,AB=8,
∵矩形ABCD,
∴AD=BC=6,AB=DC=8,
由折叠知A′B=AB=8,
在Rt△BCA′中,∠C=90°,
由勾股定理得,,
∴,
∴,
∴
(2)解:∵矩形ABCD,
∴DCAB,
∴∠ABD=∠BDC,
又由折叠知,∠ABD=∠A′BD,
∴∠BDC=∠A′BD,
∴ED=EB.
设DE=x,则EB=x,EC=8-x,
在Rt△ECB中,,即,
解得,
∴,
∴;
(3)解:根据折叠知∠A′=∠PAB=90°=∠PDE,AB=A′B=8,A′P=AP,
在△DPE和△A'FE中,
,
∴△DPE≌△A'FE(ASA),
∴PE=FE,PD=FA′,
DE+EF=A′E+PE=A′P=AP,
设AP=x,DP=A'F=6-x,CF=8-x,BF=A′B-A′F=8-(6-x)=x+2,
在Rt△CBF中,
即,
解方程得,
∴点P(0,).
27.解:(1)∵C的坐标为
∴,
∵,
∴
在矩形OABC中,
∵D点坐标为
∴
∴
(2)如图1,过D作DH⊥OA于H,则
∵四边形ABCO是矩形,
∴
∴,
∴四边形OHDC是矩形
∴OH=CD=3,DH=OC=4
由折叠可得DE=BD=5
在中,
∴
∴E点坐标为
(3),理由如下:
如图2,设直线DF与x轴交于I点,
∵B点坐标为、D点坐标为
∴,
∴
由折叠可得,,
∵轴,
∴
∴,
∴
∵,,
∴,
∴
∴
∴
∴.
一、单选题
1.如图,在平面直角坐标系中,已知点A(2,1),B(3,﹣1),将线段AB沿y轴折叠,使点B落在点B1(﹣3,﹣1)处,则点A的对应点A1坐标为( )
A.(1,﹣2) B.(﹣2,1) C.(﹣1,﹣2) D.(﹣2,﹣1)
2.如图,在平面直角坐标系中,A(0,3),B(5,3),C(5,0),点D在线段OA上,将△ABD沿着直线BD折叠,点A的对应点为E,当点E在线段OC上时,则AD的长是( )
A.1 B. C. D.2
3.如图,在平面直角坐标系中,点A的坐标是,点B的坐标是,点C是OB上一点,将沿AC折叠,点B恰好落在x轴上的点处,则点C的坐标为( )
B. C. D.
4.如图,在平面直角坐标系中,为坐标原点,,,,将沿直线折叠,使得点落在点处,与交于点,则点的纵坐标为( )
A. B. C. D.4
5.如图,把长方形纸片OABC放入平面直角坐标系中,使OC、OA分别与x轴,y轴重合,连接OB,将长方形纸片OABC沿OB折叠,使点A落在点A,的位置,A,B与x轴交于D,若点B的坐标为(4,2),则点A,的坐标为( )
A. B. C. D.
6.如图,在平面直角坐标系xOy中,正方形OABC的顶点A在x轴正半轴上,顶点C的坐标为(0,8),点M是正方形OABC的对称中心,点D是BC边上一动点(不与点B、C重合),将△ABD沿AD折叠,点B的对应点为点E,连接EM,当EM的值最小时,点D的坐标为( )
A.(4﹣4,8) B.(8﹣8,8) C.(16﹣8,8) D.(4,8)
7.如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠,折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为,则点E的坐标为( )
A. B. C. D.
8.如图,把长方形纸片放入平面直角坐标系中,使,分别落在轴、轴上,连接,将纸片沿折叠,使点落在点的位置,与轴交于点,若,则的长为( )
A. B. C. D.
9.如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点处,则点的坐标为( )
A.(2,2) B.(,3) C.(2,) D.(,)
10.如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为2﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在平面直角坐标系中,将矩形沿直线折叠(点E在边上),折叠后顶点D恰好落在边上的点F处,若点D的坐标为,则点E的坐标为____________.
12.如图,在平面直角坐标系中,长方形ABCD的边CO,OA分别在x轴、y轴上,点E在边BC上,将该长方形沿AE折叠,点B恰好落在边OC上的F处.若,,则点E的坐标是______.
如图,长方形OACB在平面直角坐标系中,O是坐标原点,点A,B分别在x轴与y轴上,已知OA=8,OB=10.把长方形沿OP折叠,点B的对应点B1恰好落在AC边上,则点P的坐标是________.
14.如图,将长方形置于平面直角坐标系中,点的坐标为(0,4),点的坐标为(m,0)(m>0),点D(m,1)在上,将长方形沿折叠压平,使点落在坐标平面内,设点的对应点为点.
(1)当时,点的坐标为__,点的坐标为__;
(2)随着的变化,点能落在轴上,此时的值是__.
15.如图,△ABC在平面直角坐标系中,AB⊥x轴,BC⊥y轴,,点B的坐标为.将△ABC沿AC折叠得到△ADC,点B落在点D的位置,AD交y轴于点E,则点D的坐标为___________.
16.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4)点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处,则点C的坐标为 _____.
17.如图,在平面直角坐标系中,已知点A(0,8),B(﹣6,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为 ___.
18.如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(2,4),则OE的长为___________.
19.如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴的负半轴、y轴的正半轴上,点D在边BC上,将该矩形沿AD折叠,点B恰好落在边OC上的E处,且△CDE为等腰直角三角形,若OA=4,则点D的坐标是_____.
20.如图所示,在平面直角坐标系中,点A的坐标为,点B在x的正半轴上,且,点E为的中点,连接,将沿折叠得到,其中交于点F,则点P的坐标是 ___________;点F的坐标是 ___________.
21.把一个矩形纸片如图放置在平面直角坐标系中,点A坐标为,点C坐,点D,E分别在边上,连接,将矩形沿着折叠后,点A落在点处,点O与点B重合,回答下面的问题:
(1)线段与相等吗?___________;
(2)点E的坐标为________________;
(3)折痕的长为_____________.
三、解答题
22.如图,在平面直角坐标系中,已知点,,连接.将沿过点的直线折叠,使点落在轴上的点处,折痕所在的直线交轴正半轴于点,求点的坐标.
23.如图,平面直角坐标系中有一个长方形OABC,OA在x轴上,OC在⊙O上,B的坐标为(8,6),将△ABC沿OB折叠,使点A与点D重合,OD与BC交于点E.
求证:△OCE≌△BDE;
求点E的坐标.
在矩形中,,,点D为边上一点,将沿直线
折叠,使点B恰好落在边上的点E处,分别以,所在的直线为x轴,y轴建立平面直角坐标系,求点D的坐标.
25.如图,长方形纸片ABCD放置在平面直角坐标系中,A与原点O重合.B、D分别在x轴和y轴上,,.
直接写出C点坐标;
如图①折叠使B落在线段AC的处,折痕为CE,求E点坐标;
如图②点P在线段DC上,若为等腰三角形,试求满足条件的所有P点坐标.
26.如图,将一张矩形纸片ABCD放入平面直角坐标系中,A(0,0),B(8,0),D(0,6),P为AD边上一点,将△ABP沿BP翻折,折叠后点A的对应点为A′.
如图①,当折叠后点A的对应点A′正好落在边DC上时,求A′C的长和A′的坐标;
如图②,当点P与点D重合时,点A的对应点为A′,A′B与DC相交于点E,求点E的坐标;
如图③,若沿BP翻折后PA′与CD相交于点E,恰好EA′=ED,BA'与CD相交于点F,求点P的坐标.(直接写出答案)
27.【问题初现】
(1)如图1,矩形OABC顶点O坐落在平面直角坐标系的原点上,C点的坐标为,,D是BC边上的点,且D的坐标是,求线段BD的长.
【问题延伸】
(2)在(1)的情况下,F为AB边上的一点,将沿直线DF折叠,若B点刚好落在x轴上的E点处,求E点的坐标.
【问题拓展】
(3)如图2,将上述情况变更为任意矩形,设B点坐标为、D点坐标为,在折叠过程中,折痕所在直线DF与y轴交于点G,当时,试判断线段OE与CD之间的数量关系,并给出证明.
答案
一、单选题
1.B 2.C 3.B 4.A 5.D 6.C 7.A 8.B 9.C 10.D
二、填空题
11.(5,)
12.
13.(5,10).
14. (3,4) (0,1)
15.
16.(0,-6)
17.
18.
19.(﹣4,).
20.
21. 相等
三、解答题
22.
解:连接交BC延长线于D,
由折叠可知,,,
,,
∴,
,
,
,
设,则,
在中,由勾股定理得,
∴,
解得,
,
故答案为:.
23.
解:(1)∵四边形OCBA为矩形,
∴CO=AB,∠OAB=∠OCE.
由翻折的性质可知∠D=∠OAB,BD=AB,
∴OC=BD,∠D=∠OCE.
∴在△OCE和△BDE中,∠D=∠OCE,∠CEO=∠DEB,OC=BD,
∴△OCE≌△BDE.
(2)∵△OCE≌△BDE,
∴EO=EB.
设CE=x,则.
在Rt△OCE中,OC=6,根据勾股定理得,,
∴,,
∴x=,
∴E(,6).
24.
解:∵矩形中,,,
∴,
∵将沿直线折叠,
∴,
在Rt△COE中
∴
设AD=m,则DE=BD=8-m,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,
即,解得m=3,
∴D(-3,-10).
25.解:(1)∵四边形ABCD是矩形,
∴CD=AB=8,BC=AD=6,
∴;
(2)在中,
∵折叠使B落在线段AC的B处,
∴,
∴
∴
∴
即
解得:
∴;
(3)如图,若为等腰三角形,
①当,即点P在AB的垂直平分线上,
∴;
②当
∴
∴;
③当BA=BP=8,即
∴
∴
∴;
综上所述,若为等腰三角形,P点坐标为:.
26.(1)解:(1)∵A(0,0),B(8,0),D(0,6),
∴AD=6,AB=8,
∵矩形ABCD,
∴AD=BC=6,AB=DC=8,
由折叠知A′B=AB=8,
在Rt△BCA′中,∠C=90°,
由勾股定理得,,
∴,
∴,
∴
(2)解:∵矩形ABCD,
∴DCAB,
∴∠ABD=∠BDC,
又由折叠知,∠ABD=∠A′BD,
∴∠BDC=∠A′BD,
∴ED=EB.
设DE=x,则EB=x,EC=8-x,
在Rt△ECB中,,即,
解得,
∴,
∴;
(3)解:根据折叠知∠A′=∠PAB=90°=∠PDE,AB=A′B=8,A′P=AP,
在△DPE和△A'FE中,
,
∴△DPE≌△A'FE(ASA),
∴PE=FE,PD=FA′,
DE+EF=A′E+PE=A′P=AP,
设AP=x,DP=A'F=6-x,CF=8-x,BF=A′B-A′F=8-(6-x)=x+2,
在Rt△CBF中,
即,
解方程得,
∴点P(0,).
27.解:(1)∵C的坐标为
∴,
∵,
∴
在矩形OABC中,
∵D点坐标为
∴
∴
(2)如图1,过D作DH⊥OA于H,则
∵四边形ABCO是矩形,
∴
∴,
∴四边形OHDC是矩形
∴OH=CD=3,DH=OC=4
由折叠可得DE=BD=5
在中,
∴
∴E点坐标为
(3),理由如下:
如图2,设直线DF与x轴交于I点,
∵B点坐标为、D点坐标为
∴,
∴
由折叠可得,,
∵轴,
∴
∴,
∴
∵,,
∴,
∴
∴
∴
∴.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
