浙教版数学九年级下册 第一章 解直角三角形复习 课件 (共13张PPT)
文档属性
| 名称 | 浙教版数学九年级下册 第一章 解直角三角形复习 课件 (共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 707.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
解直角三角形
义务教育课程标准实验教科书
浙教版《数学》九年级下册
第1章复习课
知识回顾
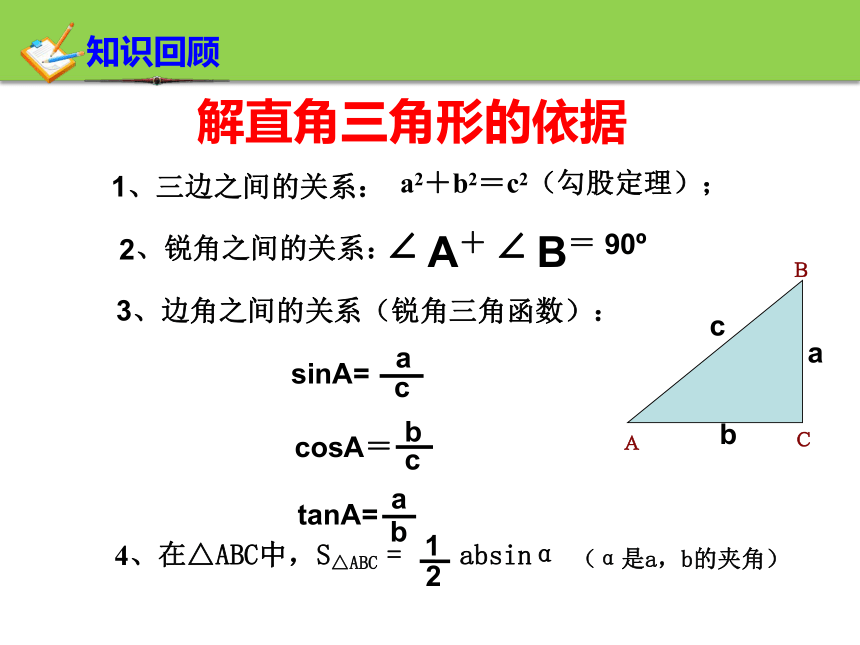
1、三边之间的关系:
a2+b2=c2(勾股定理);
2、锐角之间的关系:
∠ A+ ∠ B= 90
3、边角之间的关系(锐角三角函数):
tanA=
a
b
sinA=
a
c
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
4、在△ABC中,S△ABC = absinα
1
2
(α是a,b的夹角)
知识回顾
三角函数
角 度
sinα
cosα
tanα
1
6 0°
45 °
3 0°
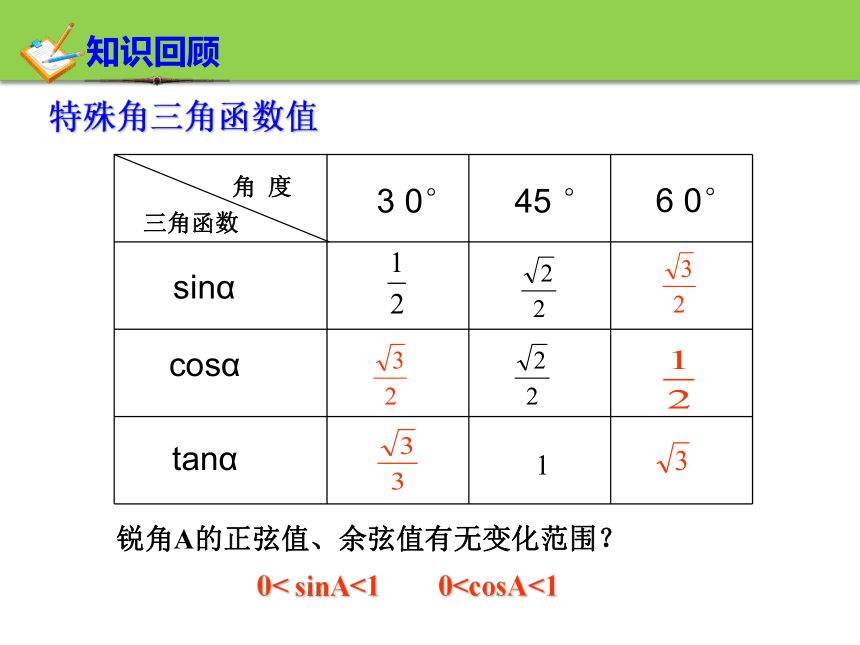
特殊角三角函数值
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1 0☆ 应用练习
1.已知角,求值
2.已知值,求角
2. 在Rt△ABC中∠C=90°,当 锐角A>45°时,sinA的值( )
(A)0<sinA< (B) <sinA<1
(C) 0<sinA< (D) <sinA<1
3. 确定值的范围
B
(A)0<cosA< (B) <cosA<1
(C) 0<cosA< (D) <cosA<1
3. 当锐角A>30°时,cosA的值( )
C
1. 已知 tanA= ,求锐角A .
知识回顾
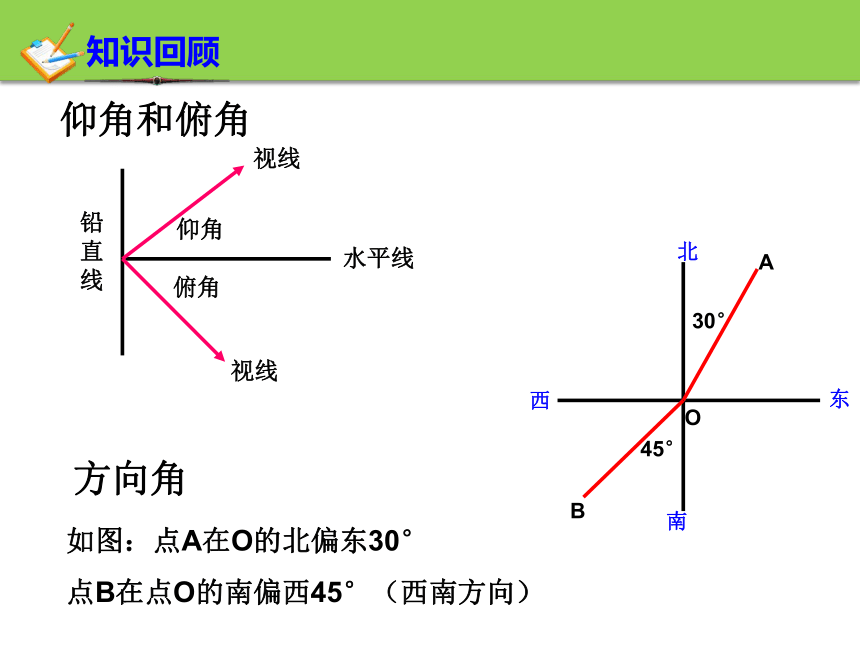
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
方向角
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
知识回顾
A
C
B
i=1︰2
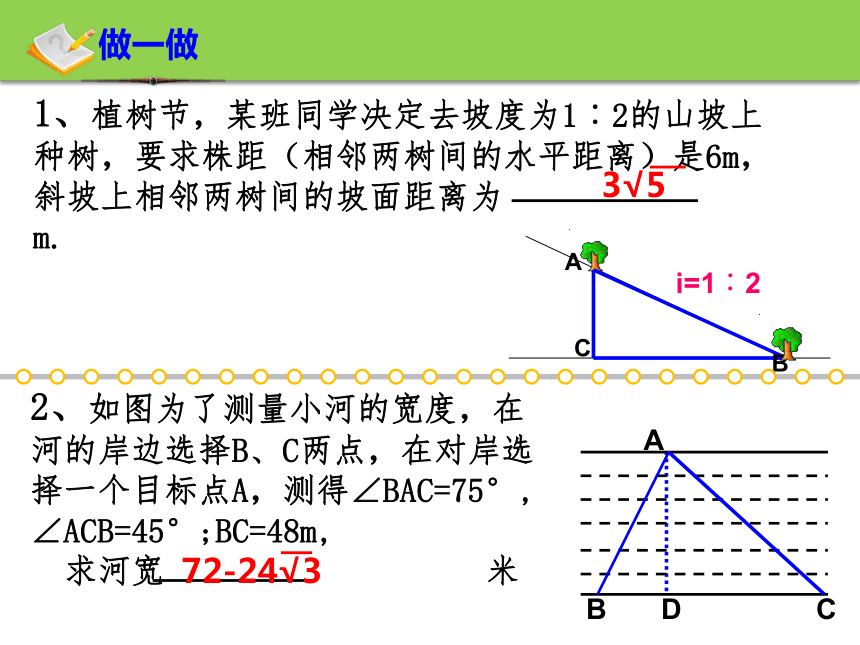
2、如图为了测量小河的宽度,在河的岸边选择B、C两点,在对岸选择一个目标点A,测得∠BAC=75°, ∠ACB=45°;BC=48m,
求河宽 米
A
B
C
D
1、植树节,某班同学决定去坡度为1︰2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,斜坡上相邻两树间的坡面距离为 m.
3√5
72-24√3
做一做
做一做
解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:
∴CE = AE2 – AC2 = 90
√
∴EF = 2CE = 2 x 90 = 180
∴A城受到沙尘暴影响的时间为
180÷12 = 15小时
答:A城将受到这次沙尘暴影响,影响的时间为15小时。
3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。
(1)A城是否受到这次沙尘暴的影响,为什么?
(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?
E
F
A
B
C
M
240
30°
做一做
4.如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竹竿长1m处,它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m.这样∠α求就可以算出来了.请你算一算.
一展身手
练习:(2006苏州)如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成500时.测得该树在斜坡上的树影BC的长为7m,求树高.(精确到0.1m)
小结
一,知识小结:
本节课主要复习勾股定理、锐角三角函数、勾股定理在解题中的应用,三角函数在解三角形中的应用。
二,方法归纳;
在涉及四边形问题时,经常把四边形进行适当分割,划分为三角形和特殊四边形,再借助特殊四边形的特征和直角三角形知识解决问题。
布置作业
1,以下列数据为三角形的边长,则不能构成直角三角形的一组是( )
A,3,4,5, B,5,12,13,
C,6 ,8 ,10 D,7,8,9
2,如果直角三角形的两条边长为3厘米、4厘米,则其周长是 。
D
12厘米或(7+√7)厘米
3,如果直角三角形的两条直角边之和为7,斜边长为5,则三角形的面积是 。
4,如图,有一张藏宝图,根据图中的数据,起点A与宝藏B的直线距离是( )
A,9 B,10
C,11 D, 12
A
B
4
2
2
6
1
2
1
6
B
布置作业
5,如图,图中直角三角形的两条直角边的长分别是6和8,则图中半圆R的面积是( )
P
R
Q
A,10 Л B, 25 Л
C,12.5 Л D, 100 Л
6, 池塘里一枝荷花高出水面20厘米,一阵劲风吹来,荷花从根部向一边倾斜,顶端与水面平齐,如图,已知荷花被风吹动的水平距离是60厘米,求池塘中水的深度。
(80厘米)
C
解直角三角形
义务教育课程标准实验教科书
浙教版《数学》九年级下册
第1章复习课
知识回顾
1、三边之间的关系:
a2+b2=c2(勾股定理);
2、锐角之间的关系:
∠ A+ ∠ B= 90
3、边角之间的关系(锐角三角函数):
tanA=
a
b
sinA=
a
c
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
4、在△ABC中,S△ABC = absinα
1
2
(α是a,b的夹角)
知识回顾
三角函数
角 度
sinα
cosα
tanα
1
6 0°
45 °
3 0°
特殊角三角函数值
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1 0
1.已知角,求值
2.已知值,求角
2. 在Rt△ABC中∠C=90°,当 锐角A>45°时,sinA的值( )
(A)0<sinA< (B) <sinA<1
(C) 0<sinA< (D) <sinA<1
3. 确定值的范围
B
(A)0<cosA< (B) <cosA<1
(C) 0<cosA< (D) <cosA<1
3. 当锐角A>30°时,cosA的值( )
C
1. 已知 tanA= ,求锐角A .
知识回顾
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
方向角
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
知识回顾
A
C
B
i=1︰2
2、如图为了测量小河的宽度,在河的岸边选择B、C两点,在对岸选择一个目标点A,测得∠BAC=75°, ∠ACB=45°;BC=48m,
求河宽 米
A
B
C
D
1、植树节,某班同学决定去坡度为1︰2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,斜坡上相邻两树间的坡面距离为 m.
3√5
72-24√3
做一做
做一做
解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:
∴CE = AE2 – AC2 = 90
√
∴EF = 2CE = 2 x 90 = 180
∴A城受到沙尘暴影响的时间为
180÷12 = 15小时
答:A城将受到这次沙尘暴影响,影响的时间为15小时。
3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。
(1)A城是否受到这次沙尘暴的影响,为什么?
(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?
E
F
A
B
C
M
240
30°
做一做
4.如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竹竿长1m处,它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m.这样∠α求就可以算出来了.请你算一算.
一展身手
练习:(2006苏州)如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成500时.测得该树在斜坡上的树影BC的长为7m,求树高.(精确到0.1m)
小结
一,知识小结:
本节课主要复习勾股定理、锐角三角函数、勾股定理在解题中的应用,三角函数在解三角形中的应用。
二,方法归纳;
在涉及四边形问题时,经常把四边形进行适当分割,划分为三角形和特殊四边形,再借助特殊四边形的特征和直角三角形知识解决问题。
布置作业
1,以下列数据为三角形的边长,则不能构成直角三角形的一组是( )
A,3,4,5, B,5,12,13,
C,6 ,8 ,10 D,7,8,9
2,如果直角三角形的两条边长为3厘米、4厘米,则其周长是 。
D
12厘米或(7+√7)厘米
3,如果直角三角形的两条直角边之和为7,斜边长为5,则三角形的面积是 。
4,如图,有一张藏宝图,根据图中的数据,起点A与宝藏B的直线距离是( )
A,9 B,10
C,11 D, 12
A
B
4
2
2
6
1
2
1
6
B
布置作业
5,如图,图中直角三角形的两条直角边的长分别是6和8,则图中半圆R的面积是( )
P
R
Q
A,10 Л B, 25 Л
C,12.5 Л D, 100 Л
6, 池塘里一枝荷花高出水面20厘米,一阵劲风吹来,荷花从根部向一边倾斜,顶端与水面平齐,如图,已知荷花被风吹动的水平距离是60厘米,求池塘中水的深度。
(80厘米)
C
