浙教版数学九年级下册 第一章 解直角三角形章末复习课 课件 (共32张PPT)
文档属性
| 名称 | 浙教版数学九年级下册 第一章 解直角三角形章末复习课 课件 (共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
第1章 解直角三角形
章末复习课
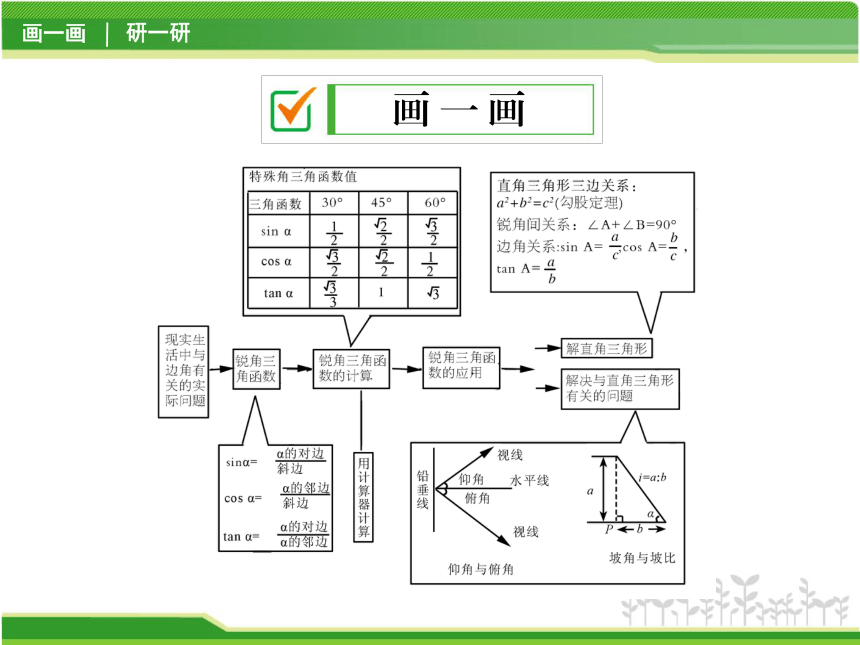
画 一 画
研 一 研
类型之一 锐角三角函数的定义
锐角三角函数是一个比值,只有弄懂它的真实含义,并严格把握定义才能求出直角三角形中的各函数值或边之值,必要时画图寻找关系.
A
【点悟】 解锐角三角函数有关的问题,首先是要理解其意义;其次是要根据题意画出示意图结合三角函数的关系式解题.
1.下列叙述错误的是 ( )
A.①②③ B.②③④
C.①②④ D.①②③④
D
类型之二 特殊三角函数值的计算
解决此类问题的关键是牢记特殊角的三角函数值.
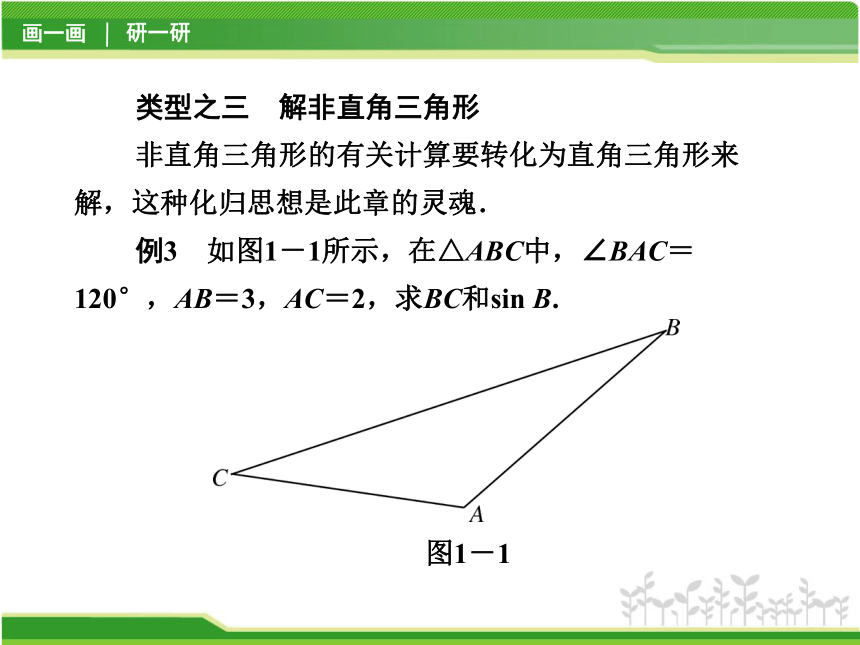
类型之三 解非直角三角形
非直角三角形的有关计算要转化为直角三角形来解,这种化归思想是此章的灵魂.
例3 如图1-1所示,在△ABC中,∠BAC=120°,AB=3,AC=2,求BC和sin B.
图1-1
【点悟】 解题规律是把BC分成两个直角三角形的两条直角边的和.这种化整为零的思想必须重视.
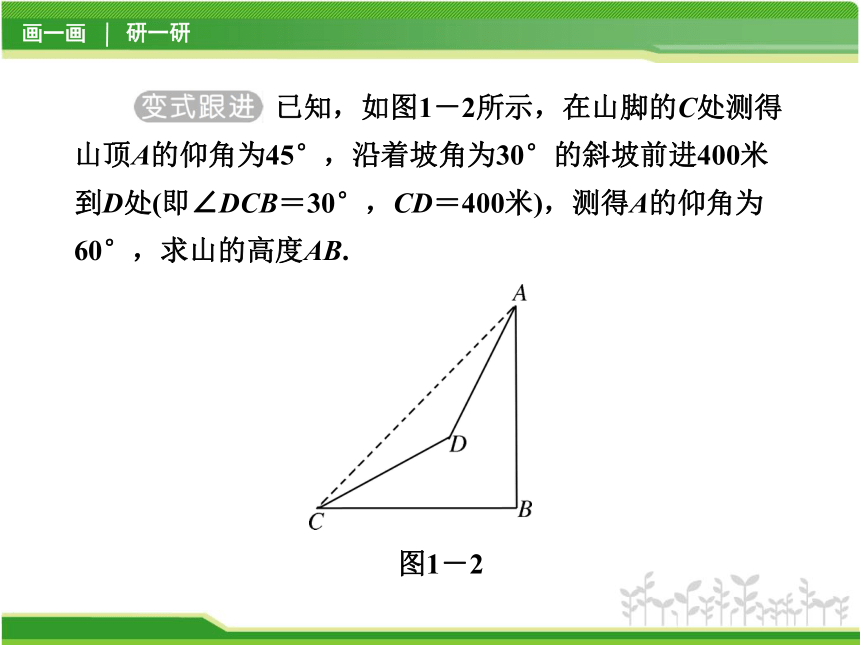
已知,如图1-2所示,在山脚的C处测得山顶A的仰角为45°,沿着坡角为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.
图1-2
【点悟】 解此题的关键是作出辅助线DF,DE,构造相应的直角三角形.
类型之四 解直角三角形的实际应用
把生活中的图形化归为直角三角形来解,同时用方程和函数的观点解决问题尤为重要.
图1-3
【解析】 本题实质是解三角形ABC,其中∠CAB=30°,∠ABC=120°.过C作CD⊥AB,交AB的延长线于D点,得Rt△BCD,Rt△ACD,再利用三角函数求解.
解: 如图所示,过点C作CD⊥AB交AB的延长线于D点,
【点悟】 解非直角三角形的一般思路是通过作高,把非直角三形转化为直角三角形,再解直角三角形.
1.为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图1-4所示).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
图1-4
图1-5
(2)已知距台风中心20 km的范围内均会受到台风的侵袭,如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
【解析】(1)建立平面直角坐标系后即可写出所求点的坐标.
【点悟】 此题考查解直角三角形在生活中的实际应用,把求非直角三角形的边长转化为解直角三角形,同时体现了建模思想和数形结合的思想.
类型之五 解直角三角形与圆的有关知识的综合运用
因为圆的直径所对的圆周角为直角,所以利用锐角三角函数解决圆的有关问题,在各地近几年的中考中经常出现,旨在考查综合能力和解决问题的能力,其重要的思想是转化.
图1-6
(1)求弦AB的长;
(2)求CD的长;
(3)求劣弧AB的长(结果保留三个有效数字,sin 53.13°≈0.8,π≈3.142).
(3)连结OA,∵sin ∠COD==0.8,
【点悟】 本题考查垂径定理、弧长公式的综合运用,关键是利用圆中的直角三角形.
图1-7
第1章 解直角三角形
章末复习课
画 一 画
研 一 研
类型之一 锐角三角函数的定义
锐角三角函数是一个比值,只有弄懂它的真实含义,并严格把握定义才能求出直角三角形中的各函数值或边之值,必要时画图寻找关系.
A
【点悟】 解锐角三角函数有关的问题,首先是要理解其意义;其次是要根据题意画出示意图结合三角函数的关系式解题.
1.下列叙述错误的是 ( )
A.①②③ B.②③④
C.①②④ D.①②③④
D
类型之二 特殊三角函数值的计算
解决此类问题的关键是牢记特殊角的三角函数值.
类型之三 解非直角三角形
非直角三角形的有关计算要转化为直角三角形来解,这种化归思想是此章的灵魂.
例3 如图1-1所示,在△ABC中,∠BAC=120°,AB=3,AC=2,求BC和sin B.
图1-1
【点悟】 解题规律是把BC分成两个直角三角形的两条直角边的和.这种化整为零的思想必须重视.
已知,如图1-2所示,在山脚的C处测得山顶A的仰角为45°,沿着坡角为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.
图1-2
【点悟】 解此题的关键是作出辅助线DF,DE,构造相应的直角三角形.
类型之四 解直角三角形的实际应用
把生活中的图形化归为直角三角形来解,同时用方程和函数的观点解决问题尤为重要.
图1-3
【解析】 本题实质是解三角形ABC,其中∠CAB=30°,∠ABC=120°.过C作CD⊥AB,交AB的延长线于D点,得Rt△BCD,Rt△ACD,再利用三角函数求解.
解: 如图所示,过点C作CD⊥AB交AB的延长线于D点,
【点悟】 解非直角三角形的一般思路是通过作高,把非直角三形转化为直角三角形,再解直角三角形.
1.为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图1-4所示).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
图1-4
图1-5
(2)已知距台风中心20 km的范围内均会受到台风的侵袭,如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
【解析】(1)建立平面直角坐标系后即可写出所求点的坐标.
【点悟】 此题考查解直角三角形在生活中的实际应用,把求非直角三角形的边长转化为解直角三角形,同时体现了建模思想和数形结合的思想.
类型之五 解直角三角形与圆的有关知识的综合运用
因为圆的直径所对的圆周角为直角,所以利用锐角三角函数解决圆的有关问题,在各地近几年的中考中经常出现,旨在考查综合能力和解决问题的能力,其重要的思想是转化.
图1-6
(1)求弦AB的长;
(2)求CD的长;
(3)求劣弧AB的长(结果保留三个有效数字,sin 53.13°≈0.8,π≈3.142).
(3)连结OA,∵sin ∠COD==0.8,
【点悟】 本题考查垂径定理、弧长公式的综合运用,关键是利用圆中的直角三角形.
图1-7
