1.1锐角三角函数(1)
图片预览



文档简介
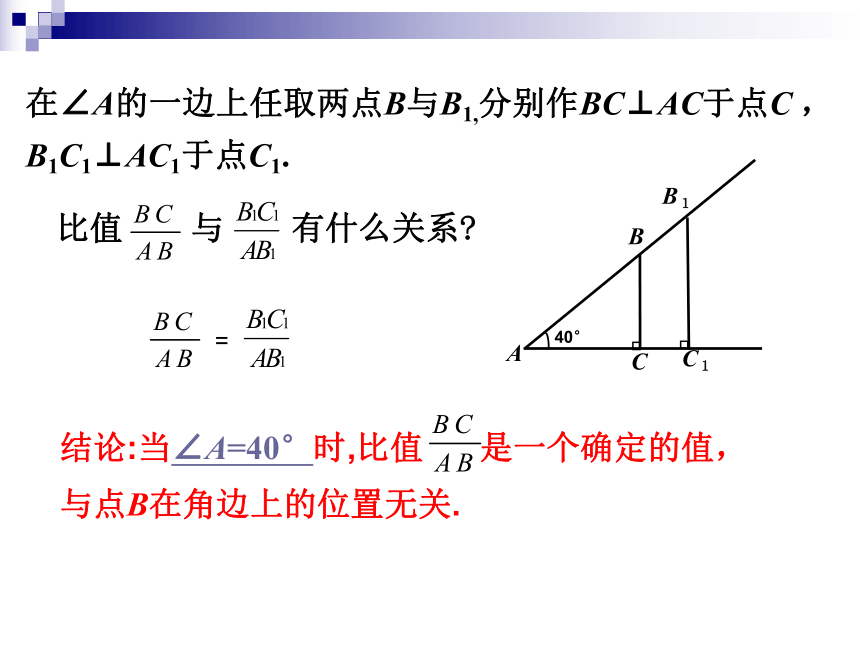
课件12张PPT。1.1 锐角三角函数九年级下册第一章 30° 40° 在∠A的一边上任取两点B与B1,分别作BC⊥AC于点C ,B1C1⊥AC1于点C1.结论:当∠A=40°时,比值 是一个确定的值, 与点B在角边上的位置无关.
比值 与 有什么关系?
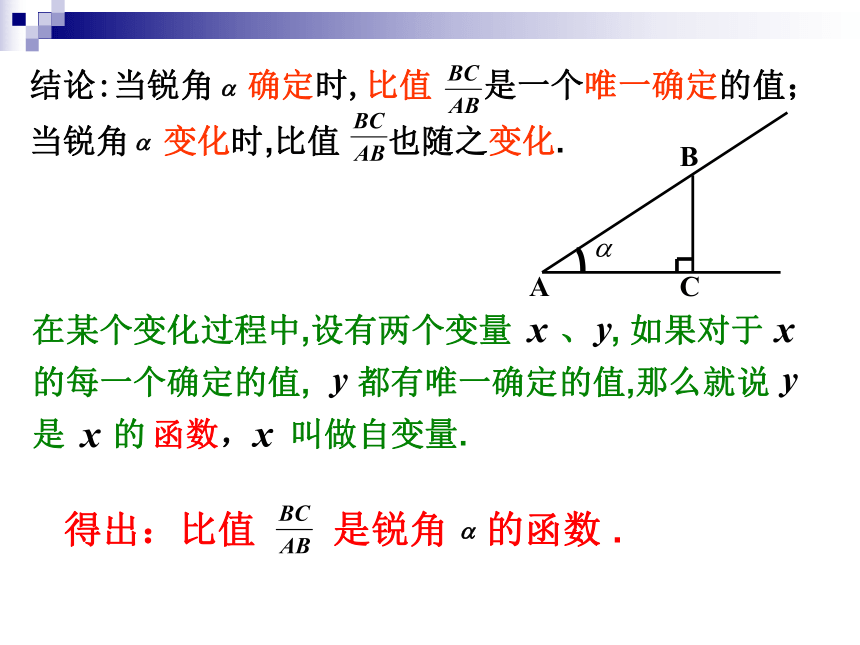
= 得出:比值 是锐角 的函数 .结论:当锐角 确定时,比值 是一个唯一确定的值; 当锐角 变化时,比值 也随之变化.在某个变化过程中,设有两个变量 、 , 如果对于 的每一个确定的值, 都有唯一确定的值,那么就说 是 的 函数, 叫做自变量.
比值 叫做∠α的正弦(sine),记做sinα.
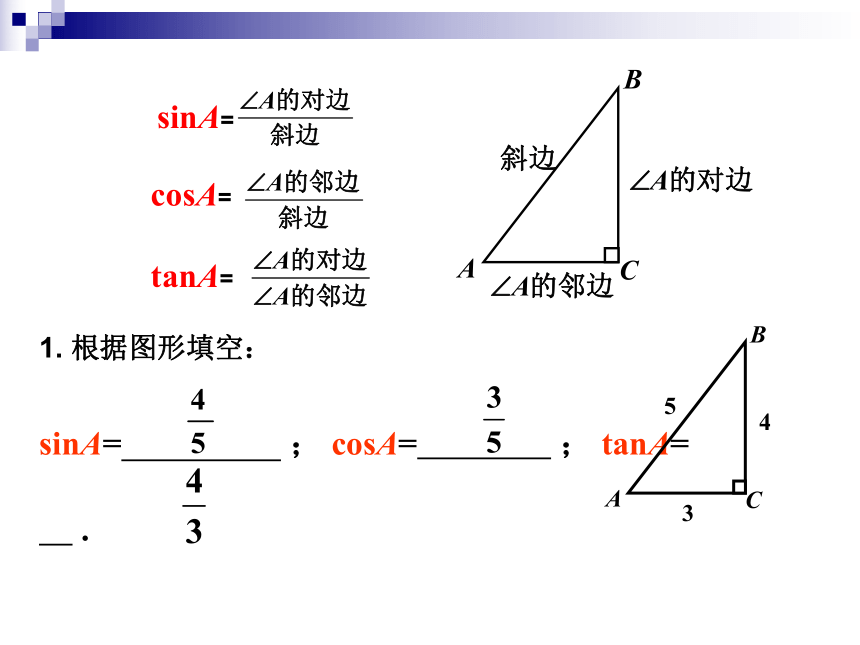
定义:即sinα=锐角 的正弦、余弦和正切统称∠ 的三角函数. sinA= cosA= tanA= 2. 如图,在Rt△ABC中,∠C= Rt ∠ ,AC=2, AB= . 求 :(1) sinA、 cosA、tanA的值;(2) sinB、 cosB、tanB的值;解: ⑴如图,在Rt△ABC中,AB= , AC=2,
∴sinA= cosA = tanA= ∴sinB= cosB = tanB= 变题一:在Rt△ABC中, ∠C=Rt∠,AC︰BC=1︰2.
求tanB、sinB、 cosB的值.解:设AC=k, 则BC=2k∴AB=∴tanB= sinB= cosB=变题二: 在Rt△ABC中, ∠C=Rt∠,sinA= ,则sinB的值为( )
(A) (B) (C) (D) A2. 一个关系:直角三角形中边角关系1. 一个概念:锐角三角函数 回顾总结: 思考: 对任意锐角 ,下列结论成立吗?请说明理由.
① 0<sin <1,
② 0<cos <1,
③sin +cos >1 ,
④tan >0作业:见作业本
比值 与 有什么关系?
= 得出:比值 是锐角 的函数 .结论:当锐角 确定时,比值 是一个唯一确定的值; 当锐角 变化时,比值 也随之变化.在某个变化过程中,设有两个变量 、 , 如果对于 的每一个确定的值, 都有唯一确定的值,那么就说 是 的 函数, 叫做自变量.
比值 叫做∠α的正弦(sine),记做sinα.
定义:即sinα=锐角 的正弦、余弦和正切统称∠ 的三角函数. sinA= cosA= tanA= 2. 如图,在Rt△ABC中,∠C= Rt ∠ ,AC=2, AB= . 求 :(1) sinA、 cosA、tanA的值;(2) sinB、 cosB、tanB的值;解: ⑴如图,在Rt△ABC中,AB= , AC=2,
∴sinA= cosA = tanA= ∴sinB= cosB = tanB= 变题一:在Rt△ABC中, ∠C=Rt∠,AC︰BC=1︰2.
求tanB、sinB、 cosB的值.解:设AC=k, 则BC=2k∴AB=∴tanB= sinB= cosB=变题二: 在Rt△ABC中, ∠C=Rt∠,sinA= ,则sinB的值为( )
(A) (B) (C) (D) A2. 一个关系:直角三角形中边角关系1. 一个概念:锐角三角函数 回顾总结: 思考: 对任意锐角 ,下列结论成立吗?请说明理由.
① 0<sin <1,
② 0<cos <1,
③sin +cos >1 ,
④tan >0作业:见作业本
