浙教版八年级数学上册试题 第5章 一次函数复习卷 (含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 第5章 一次函数复习卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 19:09:26 | ||
图片预览



文档简介
《一次函数》全章复习
一、单选题
1.若函数是正比例函数,且图象经过第二、四象限,则m的值是( )
A. B.2 C. D.3
2.若直线y=kx+k+1经过点(m,n+3)和(m+1,2n-1),且0A.33.已知一次函数,函数值y随自变量x的增大而减小,且,则函数的大致图象是( )
A. B.
C. D.
4.将一次函数的图象向右平移2个单位后与x轴交于点A,点B的坐标是,则线段的长为( )
A.5 B.7 C.1 D.
5.对于函数y=2x+1下列结论不正确的是( )
A.它的图象必过点(1,3)
B.它的图象经过一、二、三象限
C.当x>时,y>0
D.y值随x值的增大而增大
6.已知点(-2,y1),(-1,y2),(1,y3)都在直线y=-x+b上,则y1,y2,y3的值的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y3>y1>y2 D.y3>y1>y2
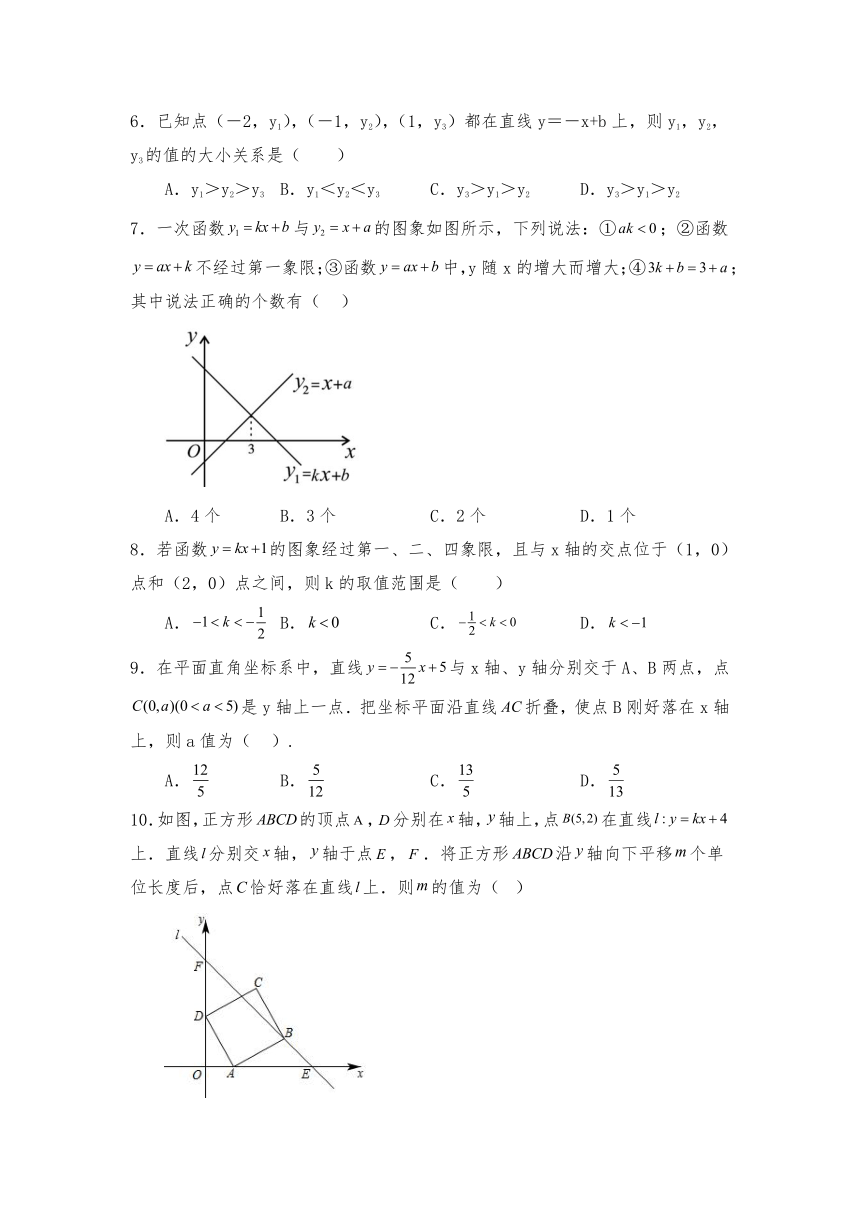
7.一次函数与的图象如图所示,下列说法:①;②函数不经过第一象限;③函数中,y随x的增大而增大;④;其中说法正确的个数有( )
A.4个 B.3个 C.2个 D.1个
8.若函数的图象经过第一、二、四象限,且与x轴的交点位于(1,0)点和(2,0)点之间,则k的取值范围是( )
A. B. C. D.
9.在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,点是y轴上一点.把坐标平面沿直线折叠,使点B刚好落在x轴上,则a值为( ).
A. B. C. D.
10.如图,正方形的顶点,分别在轴,轴上,点在直线上.直线分别交轴,轴于点,.将正方形沿轴向下平移个单位长度后,点恰好落在直线上.则的值为( )
A. B. C. D.2
二、填空题
11.在函数y=中,自变量x的取值范围是_____.
12.在平面直角坐标系中,若一次函数的图象过点,,则的值为______.
13.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于_____.
14.一次函数的图象经过第二、三、四象限,则的取值范围是__________.
15.已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所能取到的整数值为________.
16.已知点P(1,2)关于x轴的对称点为P′,且P′在直线y=kx+3上,把直线y=kx+3的图象向上平移2个单位,所得的直线解析式为_________________.
17.如图:已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴,轴分别交于点C、点D,若DB=DC,则直线CD的函数表达式为__________.
18.已知函数,当时,y有最大值6,则________.
19.函数y=(3﹣m)x+n(m,n为常数,m≠3),若2m+n=1,当﹣1≤x≤3时,函数有最大值2,则n=_____.
20.如图,直线y=﹣x+8与x轴、y轴分别交于点A、B,∠BAO的角平分线与y轴交于点M,则OM的长为_____.
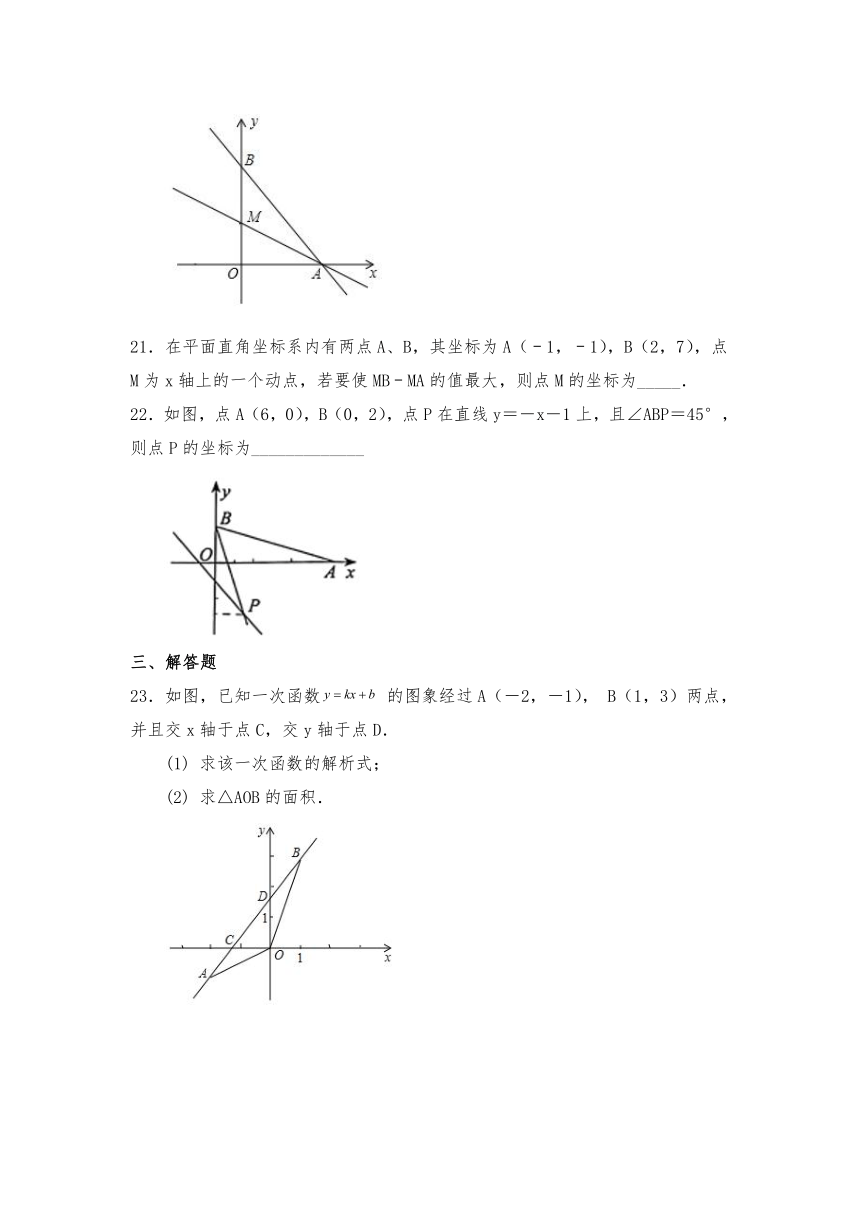
21.在平面直角坐标系内有两点A、B,其坐标为A(﹣1,﹣1),B(2,7),点M为x轴上的一个动点,若要使MB﹣MA的值最大,则点M的坐标为_____.
22.如图,点A(6,0),B(0,2),点P在直线y=-x-1上,且∠ABP=45°,则点P的坐标为_____________
三、解答题
23.如图,已知一次函数 的图象经过A(-2,-1), B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1) 求该一次函数的解析式;
(2) 求△AOB的面积.
如图,在平面直角坐标系中,直线过点且与轴交于点,把点向左平移2个单位,再向上平移4个单位,得到点.过点且与平行的直线交轴于点.
(1)求直线的解析式;
(2)直线与交于点,将直线沿方向平移,平移到经过点的位置结束,求直线在平移过程中与轴交点的横坐标的取值范围.
25.如图,已知函数的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数和y=x的图象于点C,D
(1)求点A的坐标;
(2)若OB=CD,求a的值.
26.某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和是100吨,且甲特产的销售量都不超过20吨.
(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?
(2)求该公司一个月销售这两种特产所能获得的最大总利润.
27.“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
路程(千米)
甲仓库 乙仓库
A果园 15 25
B果园 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.(温馨提示:请填写在答题卷相对应的表格内)
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园
设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
答案
一、单选题
1.A 2.B 3.A 4.A 5.C 6.A 7.C 8.A 9.A 10.B
二、填空题
11.1≤x≤2
12.
13.-3
14.m<3
15.-1
16.y=﹣5x+5.
17.
18.或
19.﹣
20.3
21.(﹣,0)
22.(3,-4)
三、解答题
23.
(1)解:把A(-2,-1),B(1,3)代入y=kx+b,得
,
解得,
∴一次函数解析式为;
(2)解:把x=0代入得,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD.
24.
解:(1)点在直线上,
,,
又点向左平移2个单位,又向上平移4个单位得到点,
,
直线与平行,
设直线的解析式为,
又直线过点,
∴2=6+b,解得b=-4,
直线的解析式为;
(2)将代入中,得,即,
故平移之后的直线的解析式为,
令,得,即,
将代入中,得,即,
平移过程中与轴交点的取值范围是:.
25.
解:(1)∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=﹣x+b得﹣1+b=2,解得b=3,
∴一次函数的解析式为y=﹣x+3,
把y=0代入y=﹣x+3得﹣x+3=0,解得x=6,
∴A点坐标为(6,0);
(2)把x=0代入y=﹣x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,﹣a+3),D点坐标为(a,a)
∴a﹣(﹣a+3)=3,
∴a=4.
26.解:(1)设这个月该公司销售甲特产吨,则销售乙特产吨,
依题意,得,
解得,则,
经检验符合题意,
所以,这个月该公司销售甲特产15吨,乙特产85吨;
(2)设一个月销售甲特产吨,则销售乙特产吨,且,
公司获得的总利润,
因为,所以随着的增大而增大,
又因为,
所以当时,公司获得的总利润的最大值为26万元,
故该公司一个月销售这两种特产能获得的最大总利润为26万元.
27.
解:(1)填表如下:
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园 80﹣x x﹣10 2×20×(80﹣x) 2×20×(x﹣10)
故答案为80﹣x,x﹣10,2×20×(80﹣x),2×20×(x﹣10);
(2)y=2×15x+2×25×(110﹣x)+2×20×(80﹣x)+2×20×(x﹣10),
即y关于x的函数表达式为y=﹣20x+8300,
∵﹣20<0,且10≤x≤80,
∴当x=80时,总运费y最省,此时y最小=﹣20×80+8300=6700.
故当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
一、单选题
1.若函数是正比例函数,且图象经过第二、四象限,则m的值是( )
A. B.2 C. D.3
2.若直线y=kx+k+1经过点(m,n+3)和(m+1,2n-1),且0
A. B.
C. D.
4.将一次函数的图象向右平移2个单位后与x轴交于点A,点B的坐标是,则线段的长为( )
A.5 B.7 C.1 D.
5.对于函数y=2x+1下列结论不正确的是( )
A.它的图象必过点(1,3)
B.它的图象经过一、二、三象限
C.当x>时,y>0
D.y值随x值的增大而增大
6.已知点(-2,y1),(-1,y2),(1,y3)都在直线y=-x+b上,则y1,y2,y3的值的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y3>y1>y2 D.y3>y1>y2
7.一次函数与的图象如图所示,下列说法:①;②函数不经过第一象限;③函数中,y随x的增大而增大;④;其中说法正确的个数有( )
A.4个 B.3个 C.2个 D.1个
8.若函数的图象经过第一、二、四象限,且与x轴的交点位于(1,0)点和(2,0)点之间,则k的取值范围是( )
A. B. C. D.
9.在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,点是y轴上一点.把坐标平面沿直线折叠,使点B刚好落在x轴上,则a值为( ).
A. B. C. D.
10.如图,正方形的顶点,分别在轴,轴上,点在直线上.直线分别交轴,轴于点,.将正方形沿轴向下平移个单位长度后,点恰好落在直线上.则的值为( )
A. B. C. D.2
二、填空题
11.在函数y=中,自变量x的取值范围是_____.
12.在平面直角坐标系中,若一次函数的图象过点,,则的值为______.
13.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于_____.
14.一次函数的图象经过第二、三、四象限,则的取值范围是__________.
15.已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所能取到的整数值为________.
16.已知点P(1,2)关于x轴的对称点为P′,且P′在直线y=kx+3上,把直线y=kx+3的图象向上平移2个单位,所得的直线解析式为_________________.
17.如图:已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴,轴分别交于点C、点D,若DB=DC,则直线CD的函数表达式为__________.
18.已知函数,当时,y有最大值6,则________.
19.函数y=(3﹣m)x+n(m,n为常数,m≠3),若2m+n=1,当﹣1≤x≤3时,函数有最大值2,则n=_____.
20.如图,直线y=﹣x+8与x轴、y轴分别交于点A、B,∠BAO的角平分线与y轴交于点M,则OM的长为_____.
21.在平面直角坐标系内有两点A、B,其坐标为A(﹣1,﹣1),B(2,7),点M为x轴上的一个动点,若要使MB﹣MA的值最大,则点M的坐标为_____.
22.如图,点A(6,0),B(0,2),点P在直线y=-x-1上,且∠ABP=45°,则点P的坐标为_____________
三、解答题
23.如图,已知一次函数 的图象经过A(-2,-1), B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1) 求该一次函数的解析式;
(2) 求△AOB的面积.
如图,在平面直角坐标系中,直线过点且与轴交于点,把点向左平移2个单位,再向上平移4个单位,得到点.过点且与平行的直线交轴于点.
(1)求直线的解析式;
(2)直线与交于点,将直线沿方向平移,平移到经过点的位置结束,求直线在平移过程中与轴交点的横坐标的取值范围.
25.如图,已知函数的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数和y=x的图象于点C,D
(1)求点A的坐标;
(2)若OB=CD,求a的值.
26.某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和是100吨,且甲特产的销售量都不超过20吨.
(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?
(2)求该公司一个月销售这两种特产所能获得的最大总利润.
27.“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
路程(千米)
甲仓库 乙仓库
A果园 15 25
B果园 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.(温馨提示:请填写在答题卷相对应的表格内)
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园
设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
答案
一、单选题
1.A 2.B 3.A 4.A 5.C 6.A 7.C 8.A 9.A 10.B
二、填空题
11.1≤x≤2
12.
13.-3
14.m<3
15.-1
16.y=﹣5x+5.
17.
18.或
19.﹣
20.3
21.(﹣,0)
22.(3,-4)
三、解答题
23.
(1)解:把A(-2,-1),B(1,3)代入y=kx+b,得
,
解得,
∴一次函数解析式为;
(2)解:把x=0代入得,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD.
24.
解:(1)点在直线上,
,,
又点向左平移2个单位,又向上平移4个单位得到点,
,
直线与平行,
设直线的解析式为,
又直线过点,
∴2=6+b,解得b=-4,
直线的解析式为;
(2)将代入中,得,即,
故平移之后的直线的解析式为,
令,得,即,
将代入中,得,即,
平移过程中与轴交点的取值范围是:.
25.
解:(1)∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=﹣x+b得﹣1+b=2,解得b=3,
∴一次函数的解析式为y=﹣x+3,
把y=0代入y=﹣x+3得﹣x+3=0,解得x=6,
∴A点坐标为(6,0);
(2)把x=0代入y=﹣x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,﹣a+3),D点坐标为(a,a)
∴a﹣(﹣a+3)=3,
∴a=4.
26.解:(1)设这个月该公司销售甲特产吨,则销售乙特产吨,
依题意,得,
解得,则,
经检验符合题意,
所以,这个月该公司销售甲特产15吨,乙特产85吨;
(2)设一个月销售甲特产吨,则销售乙特产吨,且,
公司获得的总利润,
因为,所以随着的增大而增大,
又因为,
所以当时,公司获得的总利润的最大值为26万元,
故该公司一个月销售这两种特产能获得的最大总利润为26万元.
27.
解:(1)填表如下:
运量(吨) 运费(元)
甲仓库 乙仓库 甲仓库 乙仓库
A果园 x 110﹣x 2×15x 2×25(110﹣x)
B果园 80﹣x x﹣10 2×20×(80﹣x) 2×20×(x﹣10)
故答案为80﹣x,x﹣10,2×20×(80﹣x),2×20×(x﹣10);
(2)y=2×15x+2×25×(110﹣x)+2×20×(80﹣x)+2×20×(x﹣10),
即y关于x的函数表达式为y=﹣20x+8300,
∵﹣20<0,且10≤x≤80,
∴当x=80时,总运费y最省,此时y最小=﹣20×80+8300=6700.
故当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
