浙教版八年级数学上册试题 1.5 三角形全等的判定:边角边 (含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 1.5 三角形全等的判定:边角边 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 755.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 19:21:53 | ||
图片预览




文档简介
1.5 三角形全等的判定-边角边
一、单选题
1.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
2.如图,已知,下面甲、乙、丙、丁四个三角形中,与全等的是( )
A.甲 B.乙 C.丙 D.丁
3.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
4.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7 B.5 C.3 D.2
5.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
SAS B.ASA C.AAS D.SSS
6.如图,在中,D,E是边上的两点,,则的度数为( )
A.90° B.80° C.70° D.60°
7.在△ABC中,AB=4,AC=6,AD是BC边上的中线,则AD的取值范围是( )
A.0<AD<10 B.1<AD<5 C.2<AD<10 D.0<AD<5
8.如图,在锐角△ABC中,∠BAC=45°,点B到AC的距离为2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A.1 B.1.5 C.2 D.3
9.仔细观察用直尺和圆规作一个角等于已知角的示意图,请根据三角形全等的有关知识,说明画出的依据是( )
A. B. C. D.
10.如图,是作△ABC的作图痕迹,则此作图的已知条件是( )
A.两角及夹边 B.两边及夹角
C.两角及一角的对边 D.两边及一边的对角
11.根据下列已知条件,能画出唯一的的是( )
A.,, B.,,
C.,, D.,,
二、填空题
12.如图,在中,、的平分线相交于点I,且,若,则的度数为______度.
13.如图,已知,添加一个条件______,使
14.如图,,,,若,,则___.
如图,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=NBC=∠90°,连接MN,已知MN=4,则BD=_________.
16.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=________
17.如图,在中,已知, ,.若,则的度数为__________.
18.如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,,则BF=_______.
如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAD+∠ADC=_____.
20.如图,在中,D是上的一点,,平分,交于点E,连接,若,,则_______.
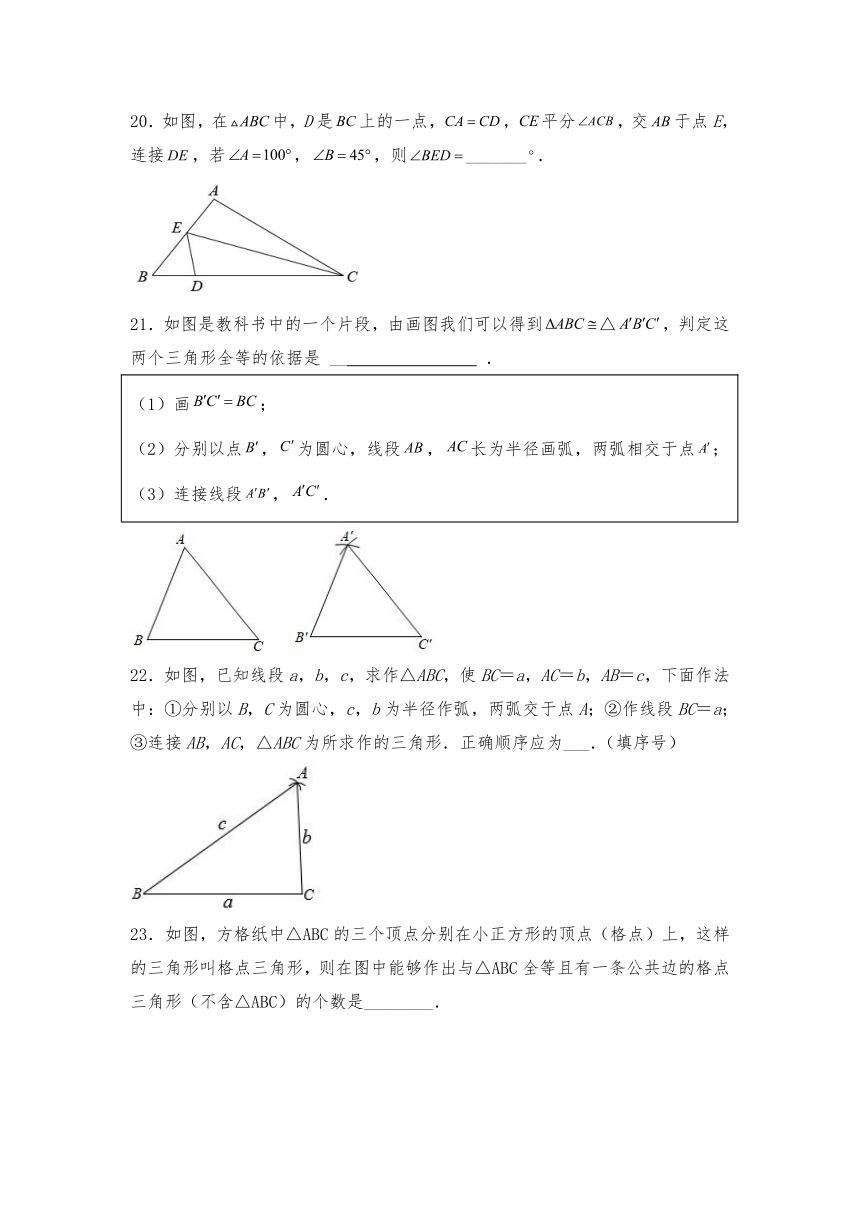
21.如图是教科书中的一个片段,由画图我们可以得到△,判定这两个三角形全等的依据是 __ .
(1)画; (2)分别以点,为圆心,线段,长为半径画弧,两弧相交于点; (3)连接线段,.
22.如图,已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法中:①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作线段BC=a;③连接AB,AC,△ABC为所求作的三角形.正确顺序应为___.(填序号)
如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是________.
三、解答题
24.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,
求证:(1)BC=EF; (2)BC∥EF.
25.已知:如图,,,.求证:.
26.在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.
(1)如图1,若∠AOB=∠COD=40°:
①AC与BD的数量关系为 ;
②∠AMB的度数为 .
(2)如图2,若∠AOB=∠COD=90°:
①判断AC与BD之间存在怎样的数量关系?并说明理由;
②求∠AMB的度数.
27.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
(1)当∠A=80°时,求∠EDC的度数;
(2)求证:CF=FG+CE.
答案
一、单选题
1.D 2.B 3.C 4.B 5.A 6.B
7.B 8.C 9.D 10.B 11.C
二、填空题
12.70
13.
14.
15.2
16.6.
17.70°
18.
19.
20.55°
21.
22.②①③
23.4
三、解答题
24.
(1)
证明:(1),
,
,
,
在与 中
,
,
.
(2),
,
.
25.
解:
在与中,
26.
(1)
解:①∵∠AOB=∠COD,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△ODB和△OCA中:OD=OC,∠DOB=∠COA,OB=OA,
∴△ODB≌△OCA(SAS),
∴AC=BD,
故答案是:AC=BD,
②∵△ODB≌△OCA,
∴∠OBD=∠OAC,
∵∠AOB=40°,
∴∠OAB+∠OBA=180°﹣∠AOB=140°,
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD,
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=140°,
∴∠MAB+∠ABM=140°,
∵在△ABM中,∠AMB+∠MAB+∠ABM=180°,
∴∠AMB=40°,
故答案是:40°;
(2)
解:①∵∠AOB=∠COD,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△ODB和△OCA中:OD=OC,∠DOB=∠COA,OB=OA,
∴△ODB≌△OCA(SAS),
∴AC=BD;
②∵△ODB≌△OCA,
∴∠OBD=∠OAC,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD,
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=90°,
∴∠MAB+∠ABM=90°,
∵在△ABM中,∠AMB+∠MAB+∠ABM=180°,
∴∠AMB=90°.
27.(1)
解:在△ABC中,∵∠A=80°,
∴,
∠ABC、∠ACB的平分线交于点D,
,
,
∠EDC=∠DBC+∠DCB
;
(2)
解:在线段上取一点,使,连接,如图所示:
平分,
,
在和中,
,
,
,
,
,
为的一个外角,
,
为的一个外角,
,
平分,
,
,
∠A=2∠BDF,
在和中,
,
,
,
,
.
一、单选题
1.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
2.如图,已知,下面甲、乙、丙、丁四个三角形中,与全等的是( )
A.甲 B.乙 C.丙 D.丁
3.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
4.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7 B.5 C.3 D.2
5.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
SAS B.ASA C.AAS D.SSS
6.如图,在中,D,E是边上的两点,,则的度数为( )
A.90° B.80° C.70° D.60°
7.在△ABC中,AB=4,AC=6,AD是BC边上的中线,则AD的取值范围是( )
A.0<AD<10 B.1<AD<5 C.2<AD<10 D.0<AD<5
8.如图,在锐角△ABC中,∠BAC=45°,点B到AC的距离为2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A.1 B.1.5 C.2 D.3
9.仔细观察用直尺和圆规作一个角等于已知角的示意图,请根据三角形全等的有关知识,说明画出的依据是( )
A. B. C. D.
10.如图,是作△ABC的作图痕迹,则此作图的已知条件是( )
A.两角及夹边 B.两边及夹角
C.两角及一角的对边 D.两边及一边的对角
11.根据下列已知条件,能画出唯一的的是( )
A.,, B.,,
C.,, D.,,
二、填空题
12.如图,在中,、的平分线相交于点I,且,若,则的度数为______度.
13.如图,已知,添加一个条件______,使
14.如图,,,,若,,则___.
如图,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=NBC=∠90°,连接MN,已知MN=4,则BD=_________.
16.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=________
17.如图,在中,已知, ,.若,则的度数为__________.
18.如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,,则BF=_______.
如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAD+∠ADC=_____.
20.如图,在中,D是上的一点,,平分,交于点E,连接,若,,则_______.
21.如图是教科书中的一个片段,由画图我们可以得到△,判定这两个三角形全等的依据是 __ .
(1)画; (2)分别以点,为圆心,线段,长为半径画弧,两弧相交于点; (3)连接线段,.
22.如图,已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法中:①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作线段BC=a;③连接AB,AC,△ABC为所求作的三角形.正确顺序应为___.(填序号)
如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是________.
三、解答题
24.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,
求证:(1)BC=EF; (2)BC∥EF.
25.已知:如图,,,.求证:.
26.在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.
(1)如图1,若∠AOB=∠COD=40°:
①AC与BD的数量关系为 ;
②∠AMB的度数为 .
(2)如图2,若∠AOB=∠COD=90°:
①判断AC与BD之间存在怎样的数量关系?并说明理由;
②求∠AMB的度数.
27.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
(1)当∠A=80°时,求∠EDC的度数;
(2)求证:CF=FG+CE.
答案
一、单选题
1.D 2.B 3.C 4.B 5.A 6.B
7.B 8.C 9.D 10.B 11.C
二、填空题
12.70
13.
14.
15.2
16.6.
17.70°
18.
19.
20.55°
21.
22.②①③
23.4
三、解答题
24.
(1)
证明:(1),
,
,
,
在与 中
,
,
.
(2),
,
.
25.
解:
在与中,
26.
(1)
解:①∵∠AOB=∠COD,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△ODB和△OCA中:OD=OC,∠DOB=∠COA,OB=OA,
∴△ODB≌△OCA(SAS),
∴AC=BD,
故答案是:AC=BD,
②∵△ODB≌△OCA,
∴∠OBD=∠OAC,
∵∠AOB=40°,
∴∠OAB+∠OBA=180°﹣∠AOB=140°,
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD,
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=140°,
∴∠MAB+∠ABM=140°,
∵在△ABM中,∠AMB+∠MAB+∠ABM=180°,
∴∠AMB=40°,
故答案是:40°;
(2)
解:①∵∠AOB=∠COD,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△ODB和△OCA中:OD=OC,∠DOB=∠COA,OB=OA,
∴△ODB≌△OCA(SAS),
∴AC=BD;
②∵△ODB≌△OCA,
∴∠OBD=∠OAC,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD,
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=90°,
∴∠MAB+∠ABM=90°,
∵在△ABM中,∠AMB+∠MAB+∠ABM=180°,
∴∠AMB=90°.
27.(1)
解:在△ABC中,∵∠A=80°,
∴,
∠ABC、∠ACB的平分线交于点D,
,
,
∠EDC=∠DBC+∠DCB
;
(2)
解:在线段上取一点,使,连接,如图所示:
平分,
,
在和中,
,
,
,
,
,
为的一个外角,
,
为的一个外角,
,
平分,
,
,
∠A=2∠BDF,
在和中,
,
,
,
,
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
