浙教版八年级数学上册试题 4.2 平面直角坐标系同步测试(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 4.2 平面直角坐标系同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览


文档简介
4.2 平面直角坐标系
一、单选题
1.如图,方格纸上有M,N两点,若以N为原点建立平面直角坐标系,则点M的坐标为(3,4);若以M点为原点建立平面直角坐标系,则点N的坐标为( )
A.(-3,-4) B.(4,0)
C.(0,-2) D.(2,0)
2.若点P是第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是 ( )
A.(2,3) B.(2,-3) C.(-3,2) D.(3,-2)
3.在平面直角坐标系中,点所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在平面直角坐标系中,点在第四象限内,则的取值可以是( )
A.1 B. C.0 D.2或﹣2
5.下列说法不正确的是( )
A.点一定在第二象限 B.点到轴的距离为2
C.若中,则点在轴上 D.若在轴上,则
6.平面直角坐标系中,点,,经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( ).
A. B. C. D.
7.已知点P的坐标为,且P到两坐标轴的距离相等,则点P的坐标为( )
A. B. C. D.或
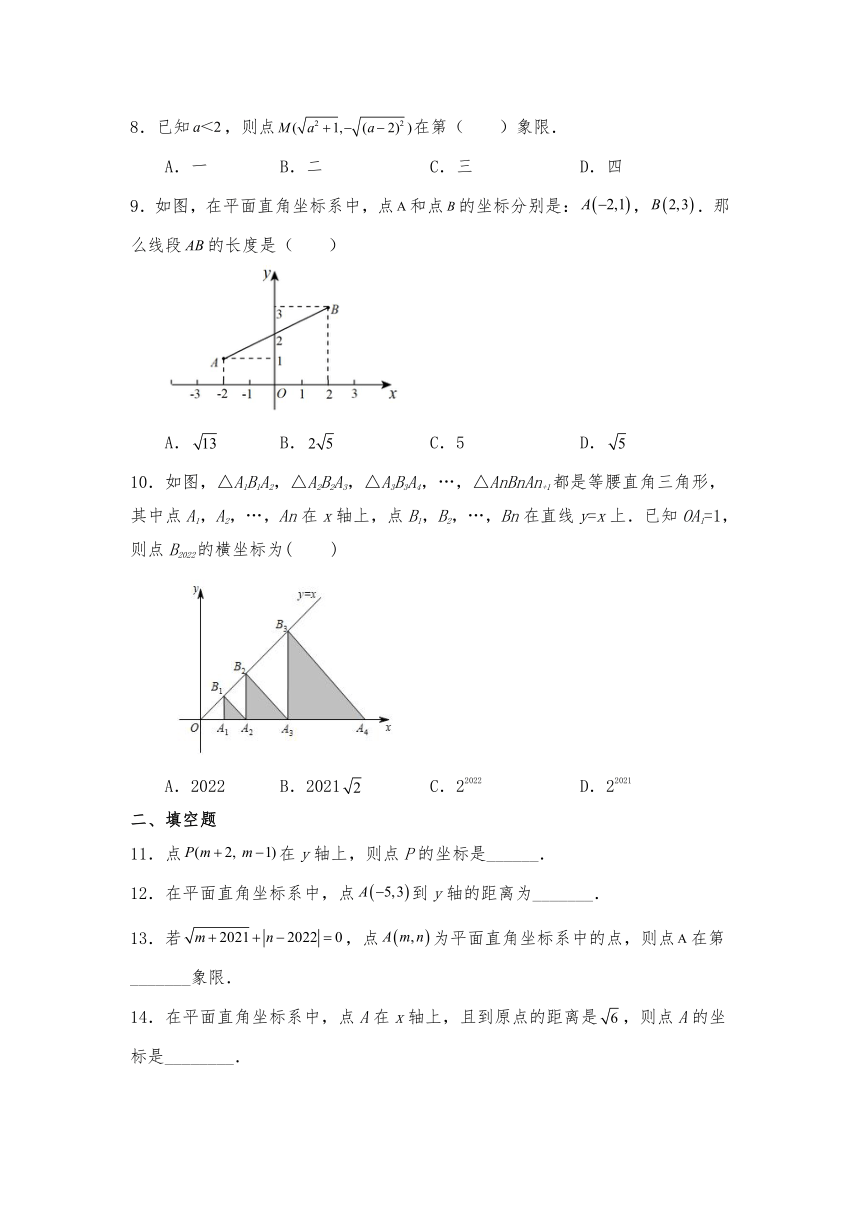
8.已知,则点在第( )象限.
A.一 B.二 C.三 D.四
9.如图,在平面直角坐标系中,点和点的坐标分别是:,.那么线段的长度是( )
A. B. C.5 D.
10.如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2022的横坐标为( )
A.2022 B.2021 C.22022 D.22021
二、填空题
11.点在y轴上,则点P的坐标是______.
12.在平面直角坐标系中,点到y轴的距离为_______.
13.若,点为平面直角坐标系中的点,则点在第_______象限.
14.在平面直角坐标系中,点A在x轴上,且到原点的距离是,则点A的坐标是________.
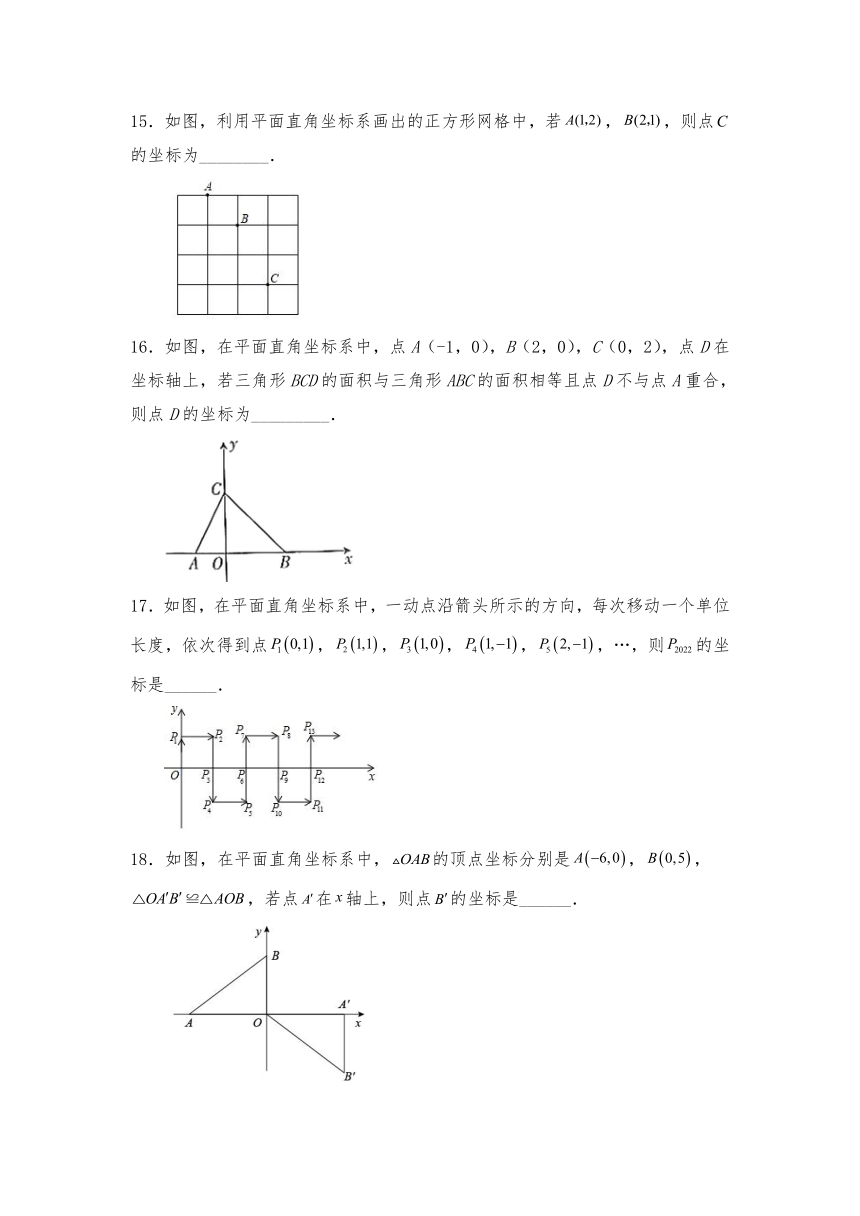
15.如图,利用平面直角坐标系画出的正方形网格中,若,,则点的坐标为________.
16.如图,在平面直角坐标系中,点A(-1,0),B(2,0),C(0,2),点D在坐标轴上,若三角形BCD的面积与三角形ABC的面积相等且点D不与点A重合,则点D的坐标为_________.
17.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点,,,,,…,则的坐标是______.
18.如图,在平面直角坐标系中,的顶点坐标分别是,,,若点在轴上,则点的坐标是______.
三、解答题
19.已知点P(2a-2,a+5),解答下列各题.
(1)点P在y轴上,则P点坐标为 ;
(2)若点P在第二象限,且它到x轴、y轴的距离相等,求a2201+2021的值.
20.已知:在平面直角坐标系中.
(1)若点Р在第三象限的角平分线上,求Р点坐标;
(2)若点Р在第四象限,且到两坐标轴的距离之和为9,求Р点坐标.
21.在平面直角坐标系中,有点A(-2,a+3),B(b,b-3).
(1)当点A在第二象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B的坐标.
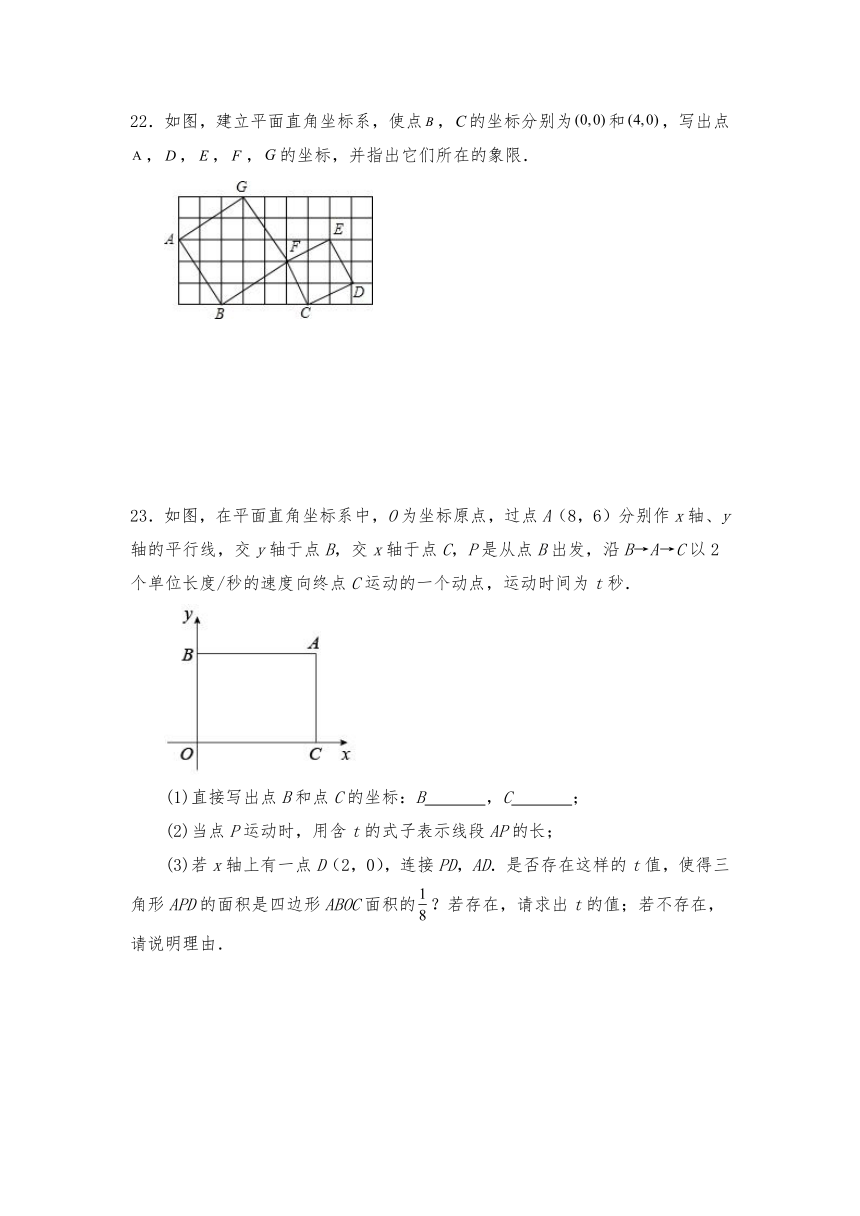
22.如图,建立平面直角坐标系,使点,的坐标分别为和,写出点,,,,的坐标,并指出它们所在的象限.
23.如图,在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t秒.
(1)直接写出点B和点C的坐标:B ,C ;
(2)当点P运动时,用含t的式子表示线段AP的长;
(3)若x轴上有一点D(2,0),连接PD,AD.是否存在这样的t值,使得三角形APD的面积是四边形ABOC面积的?若存在,请求出t的值;若不存在,请说明理由.
24.问题背景:(1)如图①,已知中,,,直线m经过点A,直线m,直线m,垂足分别为点D,E,易证:______+______.
(2)拓展延伸:如图②,将(1)中的条件改为:在中,,D,A,E三点都在直线m上,并且有,请求出DE,BD,CE三条线段的数量关系,并证明.
(3)实际应用:如图③,在中,,,点C的坐标为(-2,0),点A的坐标为(-6,3),请直接写出B点的坐标.
答案
一、单选题
1.A 2.C 3.C 4.B 5.C 6.D 7.D 8.D 9.B 10.D
二、填空题
11.
12.5
13.二
14.(-,0)或(,0)
15.
16.(5,0)或(0,5)或(0,-1)
17.(674,0)
18.(6,-5)
三、解答题
19.
(1)解:∵点P在y轴上,∴2a-2=0,∴a=1,∴a+5=6,∴P(0,6);
(2)∵点P在第二象限,∴2a-2<0, a+5>0,∵点P到x轴、y轴的距离相等,∴,∴-(2a-2)= a+5,解得:a=-1,∴a2201+2021=(-1) 2201+2021=2020.
20.(1)解:由题意,得
4x=x-3,
解得x=-1
∴.
(2)解:由题意,得
4x+[-(x-3)]=9,
则3x=6,
解得x=2,
此时点P的坐标为(8,-1).
21.
(1)解:由题意,得a+3=2,
解得a=-1;
(2)解:由题意,得|b-3|=2|b|,
解得b=-3或b=1,
当b=-3时,点B(-3,-6)在第三象限,
当b=1时,点B(1,-2)在第四象限.
综上,点B的坐标为(-3,-6)或(1,-2).
22.
解:平面直角坐标系如图所示.,,,,.点在第二象限,其余各点都在第一象限.
23.(1)解:∵AB⊥y轴于B,AC⊥x轴于C,点A(8,6),
∴∠ABO=∠BOC=∠ACO=90°,
∴四边形ABOC是长方形,
∴AB=8,AC=6,
∴B(0,6),C(8,0),
故答案为:(0,6),(8,0);
(2)解:当点P在线段BA上时,
由A(8,6),B(0,6),C(8,0)可得:AB=8,AC=6
∵AP=AB-BP,BP=2t,
∴AP=8-2t(0≤t<4);
当点P在线段AC上时,
∴AP=2t-8(4≤t≤7).
(3)解:存在;
由题意,四边形ABOC的面积=AB AC=8×6=48.
当点P在线段BA上时,
∵三角形APD的面积=AP AC,
∴×(82t)×6=×48,
解得:t=3;
当点P在线段AC上时,
∵三角形APD的面积=AP CD,CD=82=6,
∴×(2t8)×6=×48,
解得:t=5.
综上所述:当t的值为3或5时,三角形APD的面积是四边形ABOC面积的.
24.
(1)证明:∵,,
∴,
∵,
∴,
∵,
∴,
在和中
,
∴,
∴,,
∴,
即:,
故答案为:BD;CE;
(2)解:数量关系: ,
证明:在中,,
∵,,
∴,
在和中,
∴,
∴,,
∴;
(3)解:如图,作轴于E,轴于F,
由(1)可知,,
∴,,
∴,
∴点B的坐标为.
一、单选题
1.如图,方格纸上有M,N两点,若以N为原点建立平面直角坐标系,则点M的坐标为(3,4);若以M点为原点建立平面直角坐标系,则点N的坐标为( )
A.(-3,-4) B.(4,0)
C.(0,-2) D.(2,0)
2.若点P是第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是 ( )
A.(2,3) B.(2,-3) C.(-3,2) D.(3,-2)
3.在平面直角坐标系中,点所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在平面直角坐标系中,点在第四象限内,则的取值可以是( )
A.1 B. C.0 D.2或﹣2
5.下列说法不正确的是( )
A.点一定在第二象限 B.点到轴的距离为2
C.若中,则点在轴上 D.若在轴上,则
6.平面直角坐标系中,点,,经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( ).
A. B. C. D.
7.已知点P的坐标为,且P到两坐标轴的距离相等,则点P的坐标为( )
A. B. C. D.或
8.已知,则点在第( )象限.
A.一 B.二 C.三 D.四
9.如图,在平面直角坐标系中,点和点的坐标分别是:,.那么线段的长度是( )
A. B. C.5 D.
10.如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上.已知OA1=1,则点B2022的横坐标为( )
A.2022 B.2021 C.22022 D.22021
二、填空题
11.点在y轴上,则点P的坐标是______.
12.在平面直角坐标系中,点到y轴的距离为_______.
13.若,点为平面直角坐标系中的点,则点在第_______象限.
14.在平面直角坐标系中,点A在x轴上,且到原点的距离是,则点A的坐标是________.
15.如图,利用平面直角坐标系画出的正方形网格中,若,,则点的坐标为________.
16.如图,在平面直角坐标系中,点A(-1,0),B(2,0),C(0,2),点D在坐标轴上,若三角形BCD的面积与三角形ABC的面积相等且点D不与点A重合,则点D的坐标为_________.
17.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点,,,,,…,则的坐标是______.
18.如图,在平面直角坐标系中,的顶点坐标分别是,,,若点在轴上,则点的坐标是______.
三、解答题
19.已知点P(2a-2,a+5),解答下列各题.
(1)点P在y轴上,则P点坐标为 ;
(2)若点P在第二象限,且它到x轴、y轴的距离相等,求a2201+2021的值.
20.已知:在平面直角坐标系中.
(1)若点Р在第三象限的角平分线上,求Р点坐标;
(2)若点Р在第四象限,且到两坐标轴的距离之和为9,求Р点坐标.
21.在平面直角坐标系中,有点A(-2,a+3),B(b,b-3).
(1)当点A在第二象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B的坐标.
22.如图,建立平面直角坐标系,使点,的坐标分别为和,写出点,,,,的坐标,并指出它们所在的象限.
23.如图,在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t秒.
(1)直接写出点B和点C的坐标:B ,C ;
(2)当点P运动时,用含t的式子表示线段AP的长;
(3)若x轴上有一点D(2,0),连接PD,AD.是否存在这样的t值,使得三角形APD的面积是四边形ABOC面积的?若存在,请求出t的值;若不存在,请说明理由.
24.问题背景:(1)如图①,已知中,,,直线m经过点A,直线m,直线m,垂足分别为点D,E,易证:______+______.
(2)拓展延伸:如图②,将(1)中的条件改为:在中,,D,A,E三点都在直线m上,并且有,请求出DE,BD,CE三条线段的数量关系,并证明.
(3)实际应用:如图③,在中,,,点C的坐标为(-2,0),点A的坐标为(-6,3),请直接写出B点的坐标.
答案
一、单选题
1.A 2.C 3.C 4.B 5.C 6.D 7.D 8.D 9.B 10.D
二、填空题
11.
12.5
13.二
14.(-,0)或(,0)
15.
16.(5,0)或(0,5)或(0,-1)
17.(674,0)
18.(6,-5)
三、解答题
19.
(1)解:∵点P在y轴上,∴2a-2=0,∴a=1,∴a+5=6,∴P(0,6);
(2)∵点P在第二象限,∴2a-2<0, a+5>0,∵点P到x轴、y轴的距离相等,∴,∴-(2a-2)= a+5,解得:a=-1,∴a2201+2021=(-1) 2201+2021=2020.
20.(1)解:由题意,得
4x=x-3,
解得x=-1
∴.
(2)解:由题意,得
4x+[-(x-3)]=9,
则3x=6,
解得x=2,
此时点P的坐标为(8,-1).
21.
(1)解:由题意,得a+3=2,
解得a=-1;
(2)解:由题意,得|b-3|=2|b|,
解得b=-3或b=1,
当b=-3时,点B(-3,-6)在第三象限,
当b=1时,点B(1,-2)在第四象限.
综上,点B的坐标为(-3,-6)或(1,-2).
22.
解:平面直角坐标系如图所示.,,,,.点在第二象限,其余各点都在第一象限.
23.(1)解:∵AB⊥y轴于B,AC⊥x轴于C,点A(8,6),
∴∠ABO=∠BOC=∠ACO=90°,
∴四边形ABOC是长方形,
∴AB=8,AC=6,
∴B(0,6),C(8,0),
故答案为:(0,6),(8,0);
(2)解:当点P在线段BA上时,
由A(8,6),B(0,6),C(8,0)可得:AB=8,AC=6
∵AP=AB-BP,BP=2t,
∴AP=8-2t(0≤t<4);
当点P在线段AC上时,
∴AP=2t-8(4≤t≤7).
(3)解:存在;
由题意,四边形ABOC的面积=AB AC=8×6=48.
当点P在线段BA上时,
∵三角形APD的面积=AP AC,
∴×(82t)×6=×48,
解得:t=3;
当点P在线段AC上时,
∵三角形APD的面积=AP CD,CD=82=6,
∴×(2t8)×6=×48,
解得:t=5.
综上所述:当t的值为3或5时,三角形APD的面积是四边形ABOC面积的.
24.
(1)证明:∵,,
∴,
∵,
∴,
∵,
∴,
在和中
,
∴,
∴,,
∴,
即:,
故答案为:BD;CE;
(2)解:数量关系: ,
证明:在中,,
∵,,
∴,
在和中,
∴,
∴,,
∴;
(3)解:如图,作轴于E,轴于F,
由(1)可知,,
∴,,
∴,
∴点B的坐标为.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
