浙教版八年级数学上册试题 4.3.1 平面直角坐标系-存在性问题 (含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 4.3.1 平面直角坐标系-存在性问题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 21:00:23 | ||
图片预览




文档简介
4.3.1 平面直角坐标系-存在性问题
一、解答题
1.在平面直角坐标系中,点的坐标为(6,4),线段的位置如图所示,其中点的坐标为(3,0),点的坐标为.
(1)将线段平移得到线段,其中点的对应点为点,点的对应点为点;
①点在______轴上;
②点的坐标为______;
(2)在(1)的条件下,连接、,请直接写出三角形的面积;
(3)在轴上是否存在点,使得以点、点、点三点为顶点的三角形的面积为6,若存在,请直接写出点的坐标;若不存在,请说明理由.
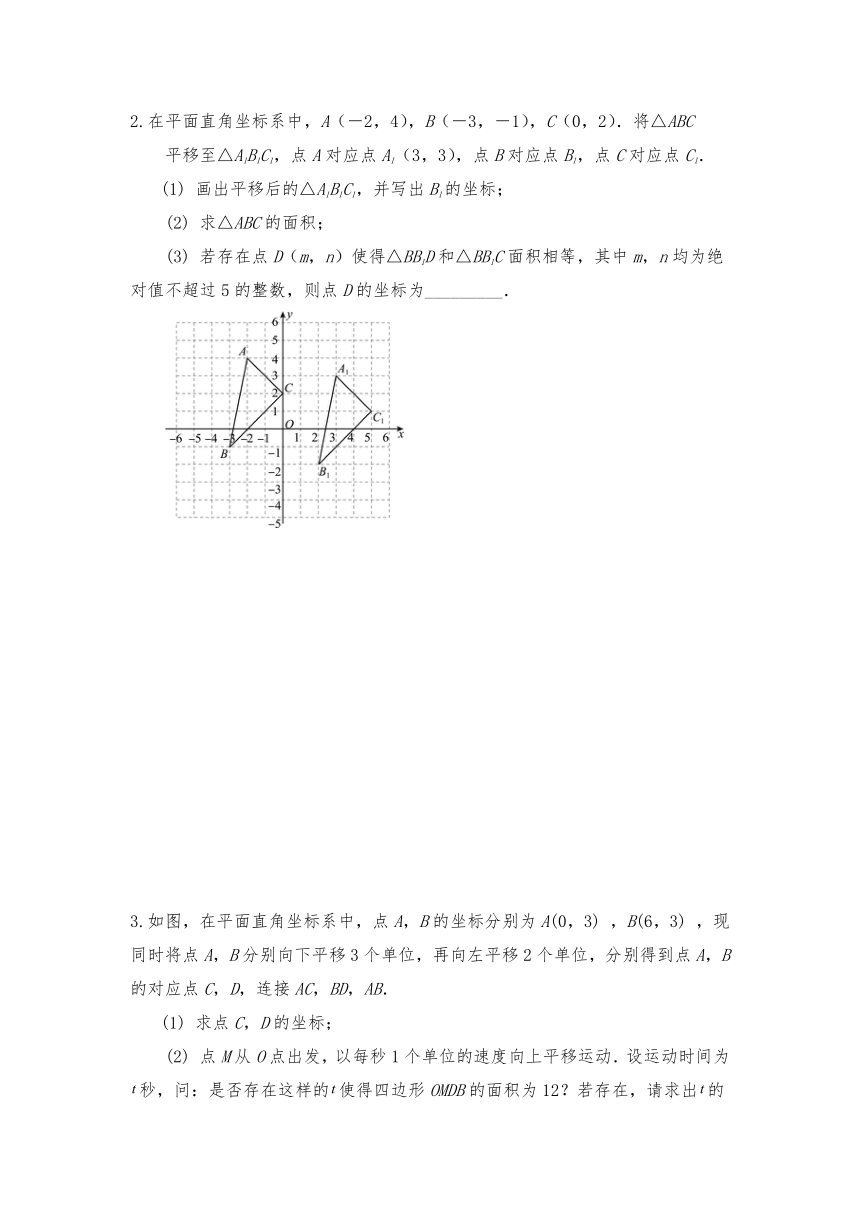
2.在平面直角坐标系中,A(-2,4),B(-3,-1),C(0,2).将△ABC
平移至△A1B1C1,点A对应点A1(3,3),点B对应点B1,点C对应点C1.
(1) 画出平移后的△A1B1C1,并写出B1的坐标;
(2) 求△ABC的面积;
(3) 若存在点D(m,n)使得△BB1D和△BB1C面积相等,其中m,n均为绝对值不超过5的整数,则点D的坐标为_________.
3.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,3) ,B(6,3) ,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1) 求点C,D的坐标;
(2) 点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为秒,问:是否存在这样的使得四边形OMDB的面积为12?若存在,请求出的值,若不存在,请说明理由.
(3) 在(2)的条件下,点M从O点出发的同时,点N从D点出发,以每秒2个单位的速度向左平移运动,当点N到达点O时运动停止.设射线BN交轴于点E.设运动时间为秒,问:的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
4.如图1,在平面直角坐标系中,点,的坐标分别是,,现同时将点,分别向上平移2个单位长度,再向右平移2个单位长度,得到,的对应点,,连接,,.
(1) 点的坐标为_________,点的坐标为_________,四边形的面积为_________;
(2) 在轴上是否存在一点,使得的面积是面积的2倍?若存在,请求出点的坐标;若不存在,请说明理由.
(3) 如图2,点是线段上一动点(,两点除外),试说明与的大小关系,并说明理由.
5.如图,在平面直角坐标系中,点,的坐标分别为,,现同时将,两点先向上平移2个单位长度,再向右平移1个单位长度,分别得到点,的对应点,,连接,,.
(1)写出点,的坐标分别是______,______;四边形的面积为______;
(2)在轴上是否存在点,连接,,使得三角形面积是三角形面积的2倍,若存在,请求出点的坐标:若不存在,请说明理由;
(3)若点是直线上一点,连接,,请你直接写出,与的数量关系.
6.在平面直角坐标系中,点A,B在y轴正半轴上,且点A在B的下方,将线段AB进行平移得到线段CD,点A的对应点为点D,点B的对应点为点C,
(1)若点A(0,1),B(0,3),D(3,2),求点C的坐标;
(2)点E是第二象限上的一个动点,过点E作EF垂直x轴于F,连接DF,DE,EC.若点A(0,m),B(0,b),C(a+b+1,m+3),D(m,﹣2m+3),三角形DEF的面积为S△DEF=,点D到直线EF的距离为3,试问是否存在m,使得S△BCE=S△ACE?若存在,请求出m的值;若不存在,请说明理由.
7.如图,三角形ABC的顶点A在原点,B,C坐标分别为B(3,0) ,C(2,2) ,将三角形ABC向左平移1个单位后再向下平移2个单位,可得到三角形.
(1)请画出平移后的三角形的图形.
(2)写出三角形各个顶点的坐标.
(3)在x轴上是否存在点P,使三角形ACP的面积等于三角形ABC面积的一半,若存在,请直接写出点P的坐标;若不存在,请说明理由.
8.如图(1),在平面直角坐标系中,已知点,,且m,n满足,将线段向右平移2个单位长度,再向上平移4个单位长度,得到线段,其中点C与点A对应,点D与点B对应,连接,.
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形的面积等于平行四边形的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且.求证:.
9.如图,已知三角形把三角形先向上平移个单位长度,再向右平移个单位长度,得到三角形.
(1)在图中画出三角形,并写出的坐标;
(2)连接,求三角形的面积;
(3)在轴上是否存在一点,使得三角形与三角形面积相等?若存在请直接写出点的坐标;若不存在,请说明理由.
10.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0) ,(3,0) ,现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
11.如图,等腰直角中,,,现将该三角形放置在平面直角坐标系中,点B坐标为,点C坐标为.过点A作轴,垂足为D.
(1) 求OD的长及点A的坐标;
(2) 取AB中点E,连接OE、DE,请你判定OE与DE的关系,并证明你的结论;
(3) 连接OA,已知,试探究在x轴上是否存在点Q,使是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
12.如图,三个顶点的坐标分别为
(1) 若与关于y轴成轴对称,在图中画出,点坐标为__________;
(2) 若直线与y轴相交于点,在y轴上是否存在点Q.使得,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3) 在x轴上找一点P,使的值最小,点P的坐标是____________.
13.如图,在平面直角坐标系中,A(-1,5) ,B(-1,0) ,C(-4,3) .
(1) 作出ABC关于y轴的对称图形;
(2) 写出点的坐标;
(3) 若坐标轴上存在一点E,使EBC是以BC边为底边的等腰三角形,直接写出点E的坐标.
(4) 在y轴上找一点P,使PA+PC的长最短.
14.在平面直角坐标系中,点O为原点,点B(0,﹣4)是y轴负半轴上一点,将点B向右平移6个单位得到点A(6,﹣4).
(1)如图1,动点P从点B出发,以每秒2个单位长度的速度沿BA方向运动,同时动点Q从点O出发,以每秒3个单位长度的速度沿y轴向上运动,当点P运动到点A时,P、Q同时停止运动,设点P运动时间为t秒.
①用含t的式子表示P,Q两点的坐标.
②是否存在t使△BPQ的面积为4t+12?若存在,求出t,并写出此时点P、Q的坐标;若不存在,说明理由.
(2)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N,若∠ODF=α,请用含α的式子表示∠ONF的大小,并说明理由.
15.如图,在平面直角坐标系中,四边形各顶点的坐标分别为,,,,现将四边形经过平移后得到四边形,点的对应点的坐标为.
(1)请直接写点、、的坐标;
(2)求四边形与四边形重叠部分的面积;
(3)在轴上是否存在一点,连接、,使,若存在这样一点,求出点的坐标;若不存在,请说明理由.
16.如图在平面直角坐标系中,点A,B的坐标分别为,.且a,b满足,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A、B的对应点C、D,连接AC,BD,CA的延长线交y轴于点K.
(1) 点P是线段CK上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段CK上移动时(不与A,C重合),请找出,,的数量关系,并证明你的结论.
(2) 连接AD,在坐标轴上是否存在点M,使的面积与的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
答案
一、解答题
1.解:(1)①点在轴上.
故答案为:.
②.
故答案为:.
(2)三角形的面积.
(3)设,则有,
解得或5,
点坐标为或.
2.解:(1)如图,△A1B1C1即为所求,B1的坐标(2,﹣2);
(2)△ABC的面积=3×52×23×31×5=6;
(3)如图,点D的坐标为(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
故答案为:(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
3.解:(1)∵点A,B的坐标分别为A(0,3) ,B(6,3) ,将点A,B分别向下平移3个单位,再向左平移2个单位
∴C(-2,0),D(4,0);
(2)解:存在;如图,过B作BH⊥OD的延长线,垂足为H.
由题意得点C和点D的坐标分别为(-2,0)和(4,0).A(0,3) ,B(6,3) ,
∴CD=6,DH=2,OD=4,AB=6,
设M点坐标为(0,t),连接MB、OB,
∴OM=t.
∵S四边形OMBD=S△OBD+S△OMB=12,
∴,
即,
解得t=2;
(3)解:不变.
理由如下:
如图所示,设运动时间为秒,OM=t,ON=4-2t(0≤t≤2) ,
过B作BH⊥OD的延长线,垂足为H,连接MB,OB,
∵=S四边形OMBN,S四边形OMBN=S△ONB+S△OMB,
∴=S△ONB+S△OMB
=
=
=6-3t+3t
=6;
∴为定值6,故其值不会变化.
4.解:(1)解:∵点A、的坐标分别是,,同时将点、分别向上平移2个单位长度,再向右平移2个单位长度得到A、的对应点、,
∴点的坐标为,点的坐标为,
;
(2)解:存在.理由如下:
设点的坐标为,
∵的面积是的面积的2倍,
∴,解得或,
∴点的坐标为或;
(3)解:,理由如下:
过点作交轴于,如图所示:
∴
∴,,
∴.
5.解:(1)点,的坐标分别为,,
将,两点先向上平移2个单位长度,再向右平移1个单位长度,分别得到点,的坐标分别是,
AB=CD,
四边形ABCD为平行四边形
四边形的面积为:;
(2)存在,理由如下:
D , C
∵AB、CD之间的距离为2,且三角形面积是三角形面积的2倍,
,
∵两个三角形等高,且
又∵
∴,
点B的坐标为
点P的坐标为或;
(3)①当点在线段上运动时,延长DQ交x轴于E点,如图2-1
;
②当点在线段延长线运动时,如图2-2
;
③当点在线段延长线运动时,如图2-3
;
综上所述:当点在线段上运动时,;
当点在线段延长线运动时,;
当点在线段延长线运动时,.
6.
解:(1)∵A(0,1),D(3,2),
∴点A先向右平移3个单位,再向上平移1个单位得到点D,
∴点B(0,3)先向右平移3个单位,再向上平移1个单位得到点C,
∴点C(3,4);
如图,存在m,使得S△BCE=S△ACE,理由如下:
∵将线段AB进行平移得到线段CD,
∴AB=CD,
∵点A(0,m),B(0,b),C(a+b+1,m+3),D(m,﹣2m+3),
∴ ,
解得: ,
∴ ,
∴,
∵EF垂直x轴,点D到直线EF的距离为3,S△DEF=,
∴ ,
解得: ,
∴ 轴,
∴点A到CE的距离为,
∵S△BCE=S△ACE,
∴点B到EC的距离为 ,
∴ ,
即 ,
解得: 或 ,
∴存在m,使得S△BCE=S△ACE,此时 或 .
7.
解:(1)如图所示:
(2)A'(﹣1,﹣2),B'(2,﹣2),C'(1,0);
(3)设P(x,0),则OP=|x|,
∵三角形ACP的面积等于三角形ABC面积的一半,
∴OP×2=AB×2,
∴|x|×2=3×2,
解得x=±,
∴P1(,0),P2(﹣,0).
8.解:(1)解:∵m,n满足,
∴,且,
∴,,
∴,,
由平移的性质得:,;
(2)解:存在,理由如下:
设,
由(1)得:,,
∴,
∵,
∴,
解得:或,
∴点P的坐标为或;
(3)证明:由平移的性质得:,
∴,
∵,
∴,
∴.
9.解:如图所示,三角形即为所求
;
;
设P(0,p)
∵△BCP与△ABC同底等高。
∴|2+p|=3,即p+2=1或p+2=-3,解得p1=1或p2=-5
∴P(0,1)或(0,-5).
答:存在.或.
10.
解:(1)依题意得:,,
;
(2)存在,当时,三角形的面积是三角形面积的2倍.
,,
,.
,
或.
11.解:(1)∵点B坐标为,点C坐标为,
∴,,
∵,
∴,
且,
∴,
且,
,
∴(AAS),
∴,
∴,,
∴点A的坐标;
(2)且;
证明:过E作轴于F,并交AD于G,
则且,
∵,,E为AB中点,
∴,
∴,,
又∵,
∴,
且和都为等腰直角三角形,
∴,,
∴,
∴;
(3)①当以点A为顶角顶点时,且OA是腰,
∵轴,
∴点,O关于直线AD对称,即:;
②当以点A为底角顶点时,且OA是腰,形成锐角三角形时,则,
∴;
③当以点A为底角顶点时,且OA是腰,形成钝角三角形时,则,
∴,
综上所述:Q的坐标为:或或.
12.
解:(1)∵与关于y轴成轴对称,三个顶点的坐标分别为, ,,
∴,,,
在网格图中画出,点坐标为(﹣4,2);
(2)存在.设Q(0,m),
∵,
∴,
∴
解得或,∴或.
(3)如图,作点B关于x轴的对称点B′,连接AB′交x轴于P,此时PA+PB的值最小,
取点F(1,-2) ,连接CF,,设CF与x轴的交点为E,
则CF=3,,
∵,
∴,
∴,
∵轴,
∴,
∴PE=CE=1,
∴OP=OE+PE=1+1=2,
∴P(2,0).
13.
(1) 解:如图1,是所求作的三角形,
(2) 解:由图1可得:
(3) 解:如图1,为等腰三角形,且为底边,
根据网格图的特点画的垂直平分线交坐标轴于
则
解:如图2,由(1)得:关于轴对称,
所以连接交轴于
则
此时最短,所以即为所求作的点.
14.
解:(1)①∵将点B(0,﹣4)向右平移6个单位得到点A(6,﹣4).
∴BA∥x轴,
∵点B(0,﹣4),动点P从点B出发,以每秒2个单位长度的速度沿BA方向运动,
∴P(2t,﹣4),
∵动点Q从点O出发,以每秒3个单位长度的速度沿y轴向上运动,
∴Q(0,3t);
②∵Q(0,3t),B(0,﹣4),
∴BQ=3t+4,BP=2t,
∴S△BPQ===3t2+4t,
∴3t2+4t=4t+12,
∴t2=4,
解得t=2,t=﹣2舍去,
∴P(4,﹣4),Q(0,6).
(2)如图2,过点N作NM∥x轴,
∵NM∥x轴,AB∥x轴,
∴NM∥AB∥x轴,
∴∠MNO=∠NOE,
∵ON是∠EOD的角平分线,
∴∠MNO=∠NOE=∠EOD,
又∵MN∥AB
∴∠MNF=∠NFA,
∵FN是∠AFD的角平分线,
∴∠MNF=∠NFA=∠AFD,
∵AB∥x轴,
∴∠OED=∠AFD,
∵∠ODF=∠EOD+∠AFD=α,
∴∠ONF=∠MNO+∠MNF=(∠EOD+∠AFD)=α.
15.解:(1)∵,,
∴平移的规则为:向右平移2个单位,向上平移一个单位;
∵,,,
∴;
(2)如图,延长交x轴于点E,过点做
由平移可知,重叠部分为平行四边形,高为2,
∴重叠部分的面积为
(3)存在;
设点的坐标为,
∵,
,
∴,
∴点的坐标为或.
16.(1)解:,证明如下:
证明:∵
∴,,解得,,
∴,,
∵将点A、B分别向左平移2个单位,再向上平移2个单位,得到对应点C、D,
∴,,
过点P作,由平移的性质可得,
∴,
∴,,
∴,
即.
(3)解:存在,M点坐标为,,,.理由如下:
的面积为,
①M在x轴上,根据的高与相等的高,
∴,
∴点M坐标为,,
②M在y轴上,的高为,的面积为5,
即
∴
又∵,
∴点M坐标为,.
故存在符合条件的M点坐标为,,,.
一、解答题
1.在平面直角坐标系中,点的坐标为(6,4),线段的位置如图所示,其中点的坐标为(3,0),点的坐标为.
(1)将线段平移得到线段,其中点的对应点为点,点的对应点为点;
①点在______轴上;
②点的坐标为______;
(2)在(1)的条件下,连接、,请直接写出三角形的面积;
(3)在轴上是否存在点,使得以点、点、点三点为顶点的三角形的面积为6,若存在,请直接写出点的坐标;若不存在,请说明理由.
2.在平面直角坐标系中,A(-2,4),B(-3,-1),C(0,2).将△ABC
平移至△A1B1C1,点A对应点A1(3,3),点B对应点B1,点C对应点C1.
(1) 画出平移后的△A1B1C1,并写出B1的坐标;
(2) 求△ABC的面积;
(3) 若存在点D(m,n)使得△BB1D和△BB1C面积相等,其中m,n均为绝对值不超过5的整数,则点D的坐标为_________.
3.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,3) ,B(6,3) ,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1) 求点C,D的坐标;
(2) 点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为秒,问:是否存在这样的使得四边形OMDB的面积为12?若存在,请求出的值,若不存在,请说明理由.
(3) 在(2)的条件下,点M从O点出发的同时,点N从D点出发,以每秒2个单位的速度向左平移运动,当点N到达点O时运动停止.设射线BN交轴于点E.设运动时间为秒,问:的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
4.如图1,在平面直角坐标系中,点,的坐标分别是,,现同时将点,分别向上平移2个单位长度,再向右平移2个单位长度,得到,的对应点,,连接,,.
(1) 点的坐标为_________,点的坐标为_________,四边形的面积为_________;
(2) 在轴上是否存在一点,使得的面积是面积的2倍?若存在,请求出点的坐标;若不存在,请说明理由.
(3) 如图2,点是线段上一动点(,两点除外),试说明与的大小关系,并说明理由.
5.如图,在平面直角坐标系中,点,的坐标分别为,,现同时将,两点先向上平移2个单位长度,再向右平移1个单位长度,分别得到点,的对应点,,连接,,.
(1)写出点,的坐标分别是______,______;四边形的面积为______;
(2)在轴上是否存在点,连接,,使得三角形面积是三角形面积的2倍,若存在,请求出点的坐标:若不存在,请说明理由;
(3)若点是直线上一点,连接,,请你直接写出,与的数量关系.
6.在平面直角坐标系中,点A,B在y轴正半轴上,且点A在B的下方,将线段AB进行平移得到线段CD,点A的对应点为点D,点B的对应点为点C,
(1)若点A(0,1),B(0,3),D(3,2),求点C的坐标;
(2)点E是第二象限上的一个动点,过点E作EF垂直x轴于F,连接DF,DE,EC.若点A(0,m),B(0,b),C(a+b+1,m+3),D(m,﹣2m+3),三角形DEF的面积为S△DEF=,点D到直线EF的距离为3,试问是否存在m,使得S△BCE=S△ACE?若存在,请求出m的值;若不存在,请说明理由.
7.如图,三角形ABC的顶点A在原点,B,C坐标分别为B(3,0) ,C(2,2) ,将三角形ABC向左平移1个单位后再向下平移2个单位,可得到三角形.
(1)请画出平移后的三角形的图形.
(2)写出三角形各个顶点的坐标.
(3)在x轴上是否存在点P,使三角形ACP的面积等于三角形ABC面积的一半,若存在,请直接写出点P的坐标;若不存在,请说明理由.
8.如图(1),在平面直角坐标系中,已知点,,且m,n满足,将线段向右平移2个单位长度,再向上平移4个单位长度,得到线段,其中点C与点A对应,点D与点B对应,连接,.
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形的面积等于平行四边形的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且.求证:.
9.如图,已知三角形把三角形先向上平移个单位长度,再向右平移个单位长度,得到三角形.
(1)在图中画出三角形,并写出的坐标;
(2)连接,求三角形的面积;
(3)在轴上是否存在一点,使得三角形与三角形面积相等?若存在请直接写出点的坐标;若不存在,请说明理由.
10.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0) ,(3,0) ,现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
11.如图,等腰直角中,,,现将该三角形放置在平面直角坐标系中,点B坐标为,点C坐标为.过点A作轴,垂足为D.
(1) 求OD的长及点A的坐标;
(2) 取AB中点E,连接OE、DE,请你判定OE与DE的关系,并证明你的结论;
(3) 连接OA,已知,试探究在x轴上是否存在点Q,使是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
12.如图,三个顶点的坐标分别为
(1) 若与关于y轴成轴对称,在图中画出,点坐标为__________;
(2) 若直线与y轴相交于点,在y轴上是否存在点Q.使得,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3) 在x轴上找一点P,使的值最小,点P的坐标是____________.
13.如图,在平面直角坐标系中,A(-1,5) ,B(-1,0) ,C(-4,3) .
(1) 作出ABC关于y轴的对称图形;
(2) 写出点的坐标;
(3) 若坐标轴上存在一点E,使EBC是以BC边为底边的等腰三角形,直接写出点E的坐标.
(4) 在y轴上找一点P,使PA+PC的长最短.
14.在平面直角坐标系中,点O为原点,点B(0,﹣4)是y轴负半轴上一点,将点B向右平移6个单位得到点A(6,﹣4).
(1)如图1,动点P从点B出发,以每秒2个单位长度的速度沿BA方向运动,同时动点Q从点O出发,以每秒3个单位长度的速度沿y轴向上运动,当点P运动到点A时,P、Q同时停止运动,设点P运动时间为t秒.
①用含t的式子表示P,Q两点的坐标.
②是否存在t使△BPQ的面积为4t+12?若存在,求出t,并写出此时点P、Q的坐标;若不存在,说明理由.
(2)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N,若∠ODF=α,请用含α的式子表示∠ONF的大小,并说明理由.
15.如图,在平面直角坐标系中,四边形各顶点的坐标分别为,,,,现将四边形经过平移后得到四边形,点的对应点的坐标为.
(1)请直接写点、、的坐标;
(2)求四边形与四边形重叠部分的面积;
(3)在轴上是否存在一点,连接、,使,若存在这样一点,求出点的坐标;若不存在,请说明理由.
16.如图在平面直角坐标系中,点A,B的坐标分别为,.且a,b满足,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A、B的对应点C、D,连接AC,BD,CA的延长线交y轴于点K.
(1) 点P是线段CK上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段CK上移动时(不与A,C重合),请找出,,的数量关系,并证明你的结论.
(2) 连接AD,在坐标轴上是否存在点M,使的面积与的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
答案
一、解答题
1.解:(1)①点在轴上.
故答案为:.
②.
故答案为:.
(2)三角形的面积.
(3)设,则有,
解得或5,
点坐标为或.
2.解:(1)如图,△A1B1C1即为所求,B1的坐标(2,﹣2);
(2)△ABC的面积=3×52×23×31×5=6;
(3)如图,点D的坐标为(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
故答案为:(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
3.解:(1)∵点A,B的坐标分别为A(0,3) ,B(6,3) ,将点A,B分别向下平移3个单位,再向左平移2个单位
∴C(-2,0),D(4,0);
(2)解:存在;如图,过B作BH⊥OD的延长线,垂足为H.
由题意得点C和点D的坐标分别为(-2,0)和(4,0).A(0,3) ,B(6,3) ,
∴CD=6,DH=2,OD=4,AB=6,
设M点坐标为(0,t),连接MB、OB,
∴OM=t.
∵S四边形OMBD=S△OBD+S△OMB=12,
∴,
即,
解得t=2;
(3)解:不变.
理由如下:
如图所示,设运动时间为秒,OM=t,ON=4-2t(0≤t≤2) ,
过B作BH⊥OD的延长线,垂足为H,连接MB,OB,
∵=S四边形OMBN,S四边形OMBN=S△ONB+S△OMB,
∴=S△ONB+S△OMB
=
=
=6-3t+3t
=6;
∴为定值6,故其值不会变化.
4.解:(1)解:∵点A、的坐标分别是,,同时将点、分别向上平移2个单位长度,再向右平移2个单位长度得到A、的对应点、,
∴点的坐标为,点的坐标为,
;
(2)解:存在.理由如下:
设点的坐标为,
∵的面积是的面积的2倍,
∴,解得或,
∴点的坐标为或;
(3)解:,理由如下:
过点作交轴于,如图所示:
∴
∴,,
∴.
5.解:(1)点,的坐标分别为,,
将,两点先向上平移2个单位长度,再向右平移1个单位长度,分别得到点,的坐标分别是,
AB=CD,
四边形ABCD为平行四边形
四边形的面积为:;
(2)存在,理由如下:
D , C
∵AB、CD之间的距离为2,且三角形面积是三角形面积的2倍,
,
∵两个三角形等高,且
又∵
∴,
点B的坐标为
点P的坐标为或;
(3)①当点在线段上运动时,延长DQ交x轴于E点,如图2-1
;
②当点在线段延长线运动时,如图2-2
;
③当点在线段延长线运动时,如图2-3
;
综上所述:当点在线段上运动时,;
当点在线段延长线运动时,;
当点在线段延长线运动时,.
6.
解:(1)∵A(0,1),D(3,2),
∴点A先向右平移3个单位,再向上平移1个单位得到点D,
∴点B(0,3)先向右平移3个单位,再向上平移1个单位得到点C,
∴点C(3,4);
如图,存在m,使得S△BCE=S△ACE,理由如下:
∵将线段AB进行平移得到线段CD,
∴AB=CD,
∵点A(0,m),B(0,b),C(a+b+1,m+3),D(m,﹣2m+3),
∴ ,
解得: ,
∴ ,
∴,
∵EF垂直x轴,点D到直线EF的距离为3,S△DEF=,
∴ ,
解得: ,
∴ 轴,
∴点A到CE的距离为,
∵S△BCE=S△ACE,
∴点B到EC的距离为 ,
∴ ,
即 ,
解得: 或 ,
∴存在m,使得S△BCE=S△ACE,此时 或 .
7.
解:(1)如图所示:
(2)A'(﹣1,﹣2),B'(2,﹣2),C'(1,0);
(3)设P(x,0),则OP=|x|,
∵三角形ACP的面积等于三角形ABC面积的一半,
∴OP×2=AB×2,
∴|x|×2=3×2,
解得x=±,
∴P1(,0),P2(﹣,0).
8.解:(1)解:∵m,n满足,
∴,且,
∴,,
∴,,
由平移的性质得:,;
(2)解:存在,理由如下:
设,
由(1)得:,,
∴,
∵,
∴,
解得:或,
∴点P的坐标为或;
(3)证明:由平移的性质得:,
∴,
∵,
∴,
∴.
9.解:如图所示,三角形即为所求
;
;
设P(0,p)
∵△BCP与△ABC同底等高。
∴|2+p|=3,即p+2=1或p+2=-3,解得p1=1或p2=-5
∴P(0,1)或(0,-5).
答:存在.或.
10.
解:(1)依题意得:,,
;
(2)存在,当时,三角形的面积是三角形面积的2倍.
,,
,.
,
或.
11.解:(1)∵点B坐标为,点C坐标为,
∴,,
∵,
∴,
且,
∴,
且,
,
∴(AAS),
∴,
∴,,
∴点A的坐标;
(2)且;
证明:过E作轴于F,并交AD于G,
则且,
∵,,E为AB中点,
∴,
∴,,
又∵,
∴,
且和都为等腰直角三角形,
∴,,
∴,
∴;
(3)①当以点A为顶角顶点时,且OA是腰,
∵轴,
∴点,O关于直线AD对称,即:;
②当以点A为底角顶点时,且OA是腰,形成锐角三角形时,则,
∴;
③当以点A为底角顶点时,且OA是腰,形成钝角三角形时,则,
∴,
综上所述:Q的坐标为:或或.
12.
解:(1)∵与关于y轴成轴对称,三个顶点的坐标分别为, ,,
∴,,,
在网格图中画出,点坐标为(﹣4,2);
(2)存在.设Q(0,m),
∵,
∴,
∴
解得或,∴或.
(3)如图,作点B关于x轴的对称点B′,连接AB′交x轴于P,此时PA+PB的值最小,
取点F(1,-2) ,连接CF,,设CF与x轴的交点为E,
则CF=3,,
∵,
∴,
∴,
∵轴,
∴,
∴PE=CE=1,
∴OP=OE+PE=1+1=2,
∴P(2,0).
13.
(1) 解:如图1,是所求作的三角形,
(2) 解:由图1可得:
(3) 解:如图1,为等腰三角形,且为底边,
根据网格图的特点画的垂直平分线交坐标轴于
则
解:如图2,由(1)得:关于轴对称,
所以连接交轴于
则
此时最短,所以即为所求作的点.
14.
解:(1)①∵将点B(0,﹣4)向右平移6个单位得到点A(6,﹣4).
∴BA∥x轴,
∵点B(0,﹣4),动点P从点B出发,以每秒2个单位长度的速度沿BA方向运动,
∴P(2t,﹣4),
∵动点Q从点O出发,以每秒3个单位长度的速度沿y轴向上运动,
∴Q(0,3t);
②∵Q(0,3t),B(0,﹣4),
∴BQ=3t+4,BP=2t,
∴S△BPQ===3t2+4t,
∴3t2+4t=4t+12,
∴t2=4,
解得t=2,t=﹣2舍去,
∴P(4,﹣4),Q(0,6).
(2)如图2,过点N作NM∥x轴,
∵NM∥x轴,AB∥x轴,
∴NM∥AB∥x轴,
∴∠MNO=∠NOE,
∵ON是∠EOD的角平分线,
∴∠MNO=∠NOE=∠EOD,
又∵MN∥AB
∴∠MNF=∠NFA,
∵FN是∠AFD的角平分线,
∴∠MNF=∠NFA=∠AFD,
∵AB∥x轴,
∴∠OED=∠AFD,
∵∠ODF=∠EOD+∠AFD=α,
∴∠ONF=∠MNO+∠MNF=(∠EOD+∠AFD)=α.
15.解:(1)∵,,
∴平移的规则为:向右平移2个单位,向上平移一个单位;
∵,,,
∴;
(2)如图,延长交x轴于点E,过点做
由平移可知,重叠部分为平行四边形,高为2,
∴重叠部分的面积为
(3)存在;
设点的坐标为,
∵,
,
∴,
∴点的坐标为或.
16.(1)解:,证明如下:
证明:∵
∴,,解得,,
∴,,
∵将点A、B分别向左平移2个单位,再向上平移2个单位,得到对应点C、D,
∴,,
过点P作,由平移的性质可得,
∴,
∴,,
∴,
即.
(3)解:存在,M点坐标为,,,.理由如下:
的面积为,
①M在x轴上,根据的高与相等的高,
∴,
∴点M坐标为,,
②M在y轴上,的高为,的面积为5,
即
∴
又∵,
∴点M坐标为,.
故存在符合条件的M点坐标为,,,.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
