浙教版八年级数学上册试题2.7.3勾股定理与方程思想(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题2.7.3勾股定理与方程思想(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 759.7KB | ||
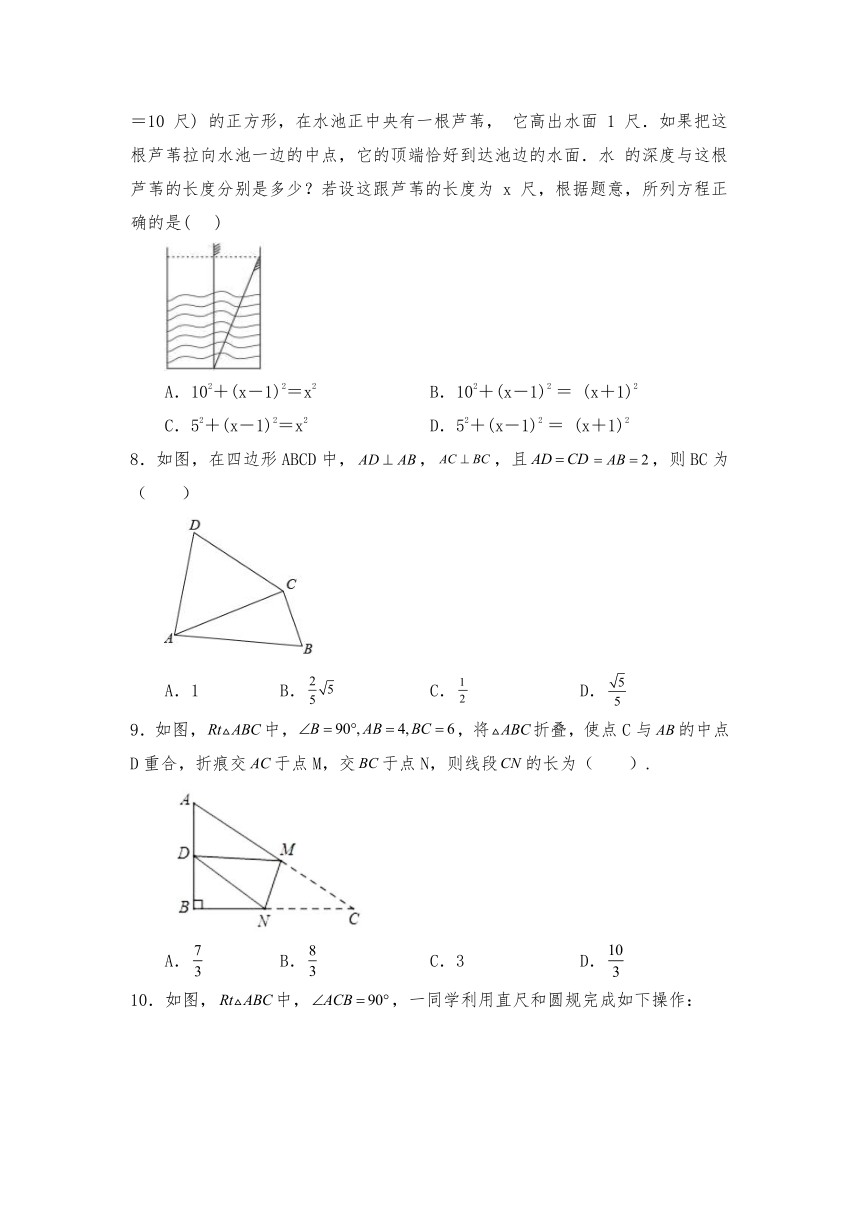
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 21:08:08 | ||
图片预览



文档简介
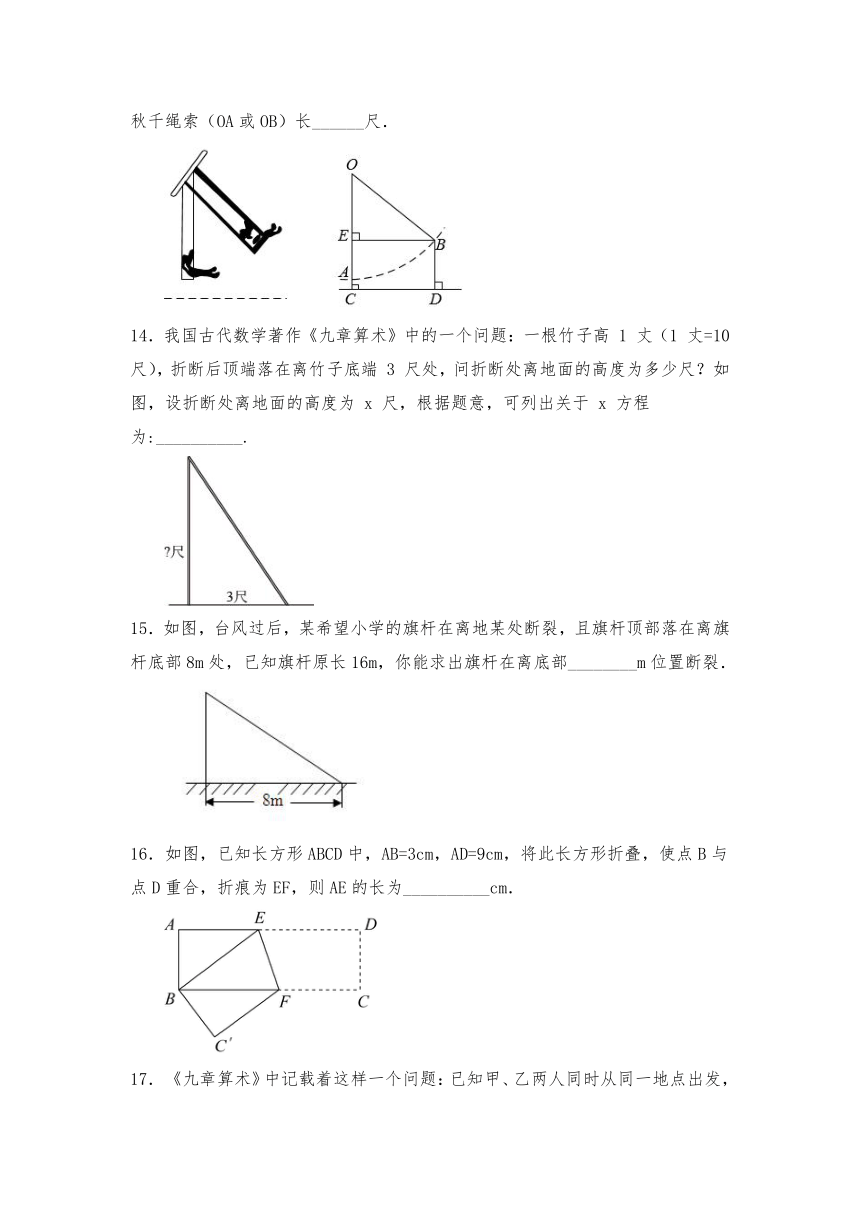
2.7.3勾股定理与方程思想
一、单选题
1.如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
2.如图,在矩形ABCD中,,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于F,,则( )
A. B.3 C. D.6
3.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为尺,将它向前水平推送尺时,即尺,秋千踏板离地的距离和身高尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为尺,根据题意可列方程为( )
B.
C. D.
4.如图,在中,,两直角边,,现将AC沿AD折叠,使点C落在斜边AB上的点E处,则CD长为( )
A. B. C. D.
5.《九章算术》是我国古代数学名著,记载着这样一个问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”大意是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?设芦苇的长度为x尺,则可列方程为( )
A.x2+52=(x+1)2 B.x2+102=(x+1)2
C.x2﹣52=(x﹣1)2 D.x2﹣102=(x﹣1)2
6.如图,嘉嘉在A时测得一棵4米高的树的影长为,若A时和B时两次日照的光线互相垂直,则B时的影长为( )
A. B. C. D.
7.我国古代数学著作《九章算术》中有这样一个问题: “今有方池一丈,葭生其中央,出水一 尺,引葭赴岸,适与岸齐.水深、葭长各几何? ”.其大意是:如图,有一个水池,水面是 一个边长为 10 尺 (丈、尺是长度单位,1 丈=10 尺) 的正方形,在水池正中央有一根芦苇, 它高出水面 1 尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水 的深度与这根芦苇的长度分别是多少?若设这跟芦苇的长度为 x 尺,根据题意,所列方程正 确的是( )
A.102+(x-1)2=x2 B.102+(x-1)2 = (x+1)2
C.52+(x-1)2=x2 D.52+(x-1)2 = (x+1)2
8.如图,在四边形ABCD中,,,且,则BC为( )
A.1 B. C. D.
9.如图,中,,将折叠,使点C与的中点D重合,折痕交于点M,交于点N,则线段的长为( ).
A. B. C.3 D.
10.如图,中,,一同学利用直尺和圆规完成如下操作:
①以点C为圆心,以CB为半径画弧,交AB于点G;分别以点G、B为圆心,以大于的长为半径画弧,两弧交点K,作射线CK;
②以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于N,分别以M、N为圆心,以大于的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E.
请你观察图形,根据操作结果解答下列问题;过点D作交AB的延长线于点F,若,,则CE的长为( )
A.13 B. C. D.
二、填空题
11.在Rt△ABC中,∠C=90°,且AC∶BC=1∶7,AB=100米,则AC=_________米.
12.如图,在△ABC中,AB=10,BC=9, AC=17,则BC边上的高为_______.
明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地……”翻译成现代文为:如图,秋千绳索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(AC=1尺).将它往前推进两步(EB⊥OC于点E,且EB=10尺),踏板升高到点B位置,此时踏板离地五尺(BD=CE=5尺),则秋千绳索(OA或OB)长______尺.
14.我国古代数学著作《九章算术》中的一个问题:一根竹子高 1 丈(1 丈=10 尺),折断后顶端落在离竹子底端 3 尺处,问折断处离地面的高度为多少尺?如图,设折断处离地面的高度为 x 尺,根据题意,可列出关于 x 方程为:__________.
15.如图,台风过后,某希望小学的旗杆在离地某处断裂,且旗杆顶部落在离旗杆底部8m处,已知旗杆原长16m,你能求出旗杆在离底部________m位置断裂.
16.如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为__________cm.
《九章算术》中记载着这样一个问题:已知甲、乙两人同时从同一地点出发,甲的速度为7步/分,乙的速度为3步/分,乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇,那么相遇时,甲、乙各走了多远?解:如图,设甲乙两人出发后x分钟相遇.根据勾股定理可列得方程为______.
18.如图,的两直角边AC、BC的长分别为6、8,按图示那样折叠,使点A与点B重合,折痕为DE,则______.
19.如图,矩形ABCD中,AD=6,AB=8.点E为边DC上的一个动点,△AD'E与△ADE关于直线AE对称,当△CD'E为直角三角形时,DE的长为__.
三、解答题
20.如图,在一次地震中,一棵垂直于地面且高度为16米的大树被折断,树的顶部落在离树根8米处,即,求这棵树在离地面多高处被折断(即求AC的长度)?
21.如图,烟台市正政府决定在相距50km的A、B两村之间的公路旁E点,修建一个大樱桃批发市场,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么大樱桃批发市场E应建什么位置才能符合要求?
22.某海上有一小岛,为了测量小岛两端A,B的距离,测量人员设计了一种测量方法,如图,已知B是CD的中点,E是BA延长线上的一点,且∠CED=90°,测得AE=16.6海里,DE=60海里,CE=80海里.
(1) 求小岛两端A,B的距离.
(2) 过点C作CF⊥AB交AB的延长线于点F,求值.
23.如图,有一架秋千,当他静止时,踏板离地的垂直高度,将他往前推送(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
24.在△ABC中,,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为直角三角形时,求t的值.
已知m>0,若3m+2,4m+8,5m+8是一组勾股数,求m的值.
26.(1)图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.
(2)如果(1)中分割成的直角三角形两直角边分别为a,b斜边为c.请你利用图2中拼成的大正方形证明勾股定理.
(3)应用:测量旗杆的高度:校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度).
27.如图,某商家想在商场大楼上悬挂一块广告牌,广告牌高.根据商场规定广告牌最高点不得高于地面20m,经测量,测角仪支架高,在F处测得广告牌底部点B的仰角为30°,在E处测得标语牌顶部点A的仰角为45°,,请计算说明,商家这样放广告牌是否符合规定?(图中点A,B,C,D,E,F,G,H在同一平面内)
28.如图所示,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
(1) 出发3s后,求PQ的长;
(2) 当点Q在边BC上运动时,出发多久后,△PQB能形成等腰三角形?
(3) 当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
答案
一、单选题
1.C 2.A 3.C 4.A 5.C 6.A 7.C 8.B 9.D 10.D
二、填空题
11.
12.8
13.
14.
15.6
16.4
17.
18.
19.3或6
三、解答题
20.
设,利用勾股定理列方程求解即可.
解:设,
∵在中,,
∴,
∴.
答:这棵树在离地面6米处被折断
21.
解:设大樱桃批发市场E应建在离A站x千米的地方,则千米.
在直角中,根据勾股定理得:,
∴,
在直角中,根据勾股定理得:,
∴.
又∵C、D两村到E点的距离相等,
∴,
∴,
所以,
解得.
∴大樱桃批发市场E应建在离A站20千米的地方.
22.
解:(1)在△DCE中,∠CED=90°,DE=60海里,CE=80海里,
由勾股定理可得(海里),
∵B是CD的中点,
∴(海里),
∴AB=BE-AE=50-16.6=33.4(海里)
答:小岛两端A、B的距离是33.4海里;
(2)设BF=x海里.
在Rt△CFB中,∠CFB=90°,
∴CF2=CB2-BF2=502-x2=2500-x2,
在Rt△CFE中,∠CFE=90°,
∴CF2+EF2=CE2,即,
解得x=14,
∴
答:值为.
23.解:设秋千的绳索长为,则,
,
在中,
,即,
解得,
答:绳索的长度是.
24.解:在Rt△ABC中,由勾股定理得:,
∴BC=4cm,
由题意得:BP=tcm.,
①当∠APB为直角时,
如图①,点P与点C重合,
BP=BC=4cm,
∴t=4;
②当∠BAP为直角时,
如图②,BP=tcm.CP=(t-4)cm,AC=3cm,
在Rt△ACP中,,
在Rt△BAP中,,
即,
解得,
答:当△ABP为直角三角形时,t=4或.
25.
解: m>0, 3m+2,4m+8,5m+8是一组勾股数,
(3m+2)2+(4m+8)2=(5m+8)2,
解得:m=1.
26.
解:(1)如图
(2)
=
=
∴
(3)如图,在四边形ABCD中,AB⊥BC,DC⊥BC,AD比AB长0.5米,BC=4米,CD=0.5米,求AB的长.
解:过点D作DE⊥AB,垂足为E
∵ AB⊥BC,DC⊥BC
∴∠B=∠C=∠DEB=90
∴四边形BCDE是矩形
∴ED=BC=4,BE=DC=0.5
设AB=,则AD=+0.5,AE=-0.5
在RtΔAED中
AD2=AE2+ED2
(+0.5)2=(-0.5)2+42
解得:=8
答:旗杆的高为8米.
27.解:设
且
解得:
商家这样放广告牌不符合规定.
28.
解:(1)当t=3时,则AP=3,BQ=2t=6,
∵AB=16cm,
∴BP=AB﹣AP=16﹣3=13(cm),
在Rt△BPQ中,PQ===(cm).
(2)由题意可知AP=t,BQ=2t,
∵AB=16,
∴BP=AB﹣AP=16﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即16﹣t=2t,解得t=,
∴出发秒后△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则BE=,
∴CE===,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
一、单选题
1.如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
2.如图,在矩形ABCD中,,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于F,,则( )
A. B.3 C. D.6
3.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为尺,将它向前水平推送尺时,即尺,秋千踏板离地的距离和身高尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为尺,根据题意可列方程为( )
B.
C. D.
4.如图,在中,,两直角边,,现将AC沿AD折叠,使点C落在斜边AB上的点E处,则CD长为( )
A. B. C. D.
5.《九章算术》是我国古代数学名著,记载着这样一个问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”大意是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?设芦苇的长度为x尺,则可列方程为( )
A.x2+52=(x+1)2 B.x2+102=(x+1)2
C.x2﹣52=(x﹣1)2 D.x2﹣102=(x﹣1)2
6.如图,嘉嘉在A时测得一棵4米高的树的影长为,若A时和B时两次日照的光线互相垂直,则B时的影长为( )
A. B. C. D.
7.我国古代数学著作《九章算术》中有这样一个问题: “今有方池一丈,葭生其中央,出水一 尺,引葭赴岸,适与岸齐.水深、葭长各几何? ”.其大意是:如图,有一个水池,水面是 一个边长为 10 尺 (丈、尺是长度单位,1 丈=10 尺) 的正方形,在水池正中央有一根芦苇, 它高出水面 1 尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水 的深度与这根芦苇的长度分别是多少?若设这跟芦苇的长度为 x 尺,根据题意,所列方程正 确的是( )
A.102+(x-1)2=x2 B.102+(x-1)2 = (x+1)2
C.52+(x-1)2=x2 D.52+(x-1)2 = (x+1)2
8.如图,在四边形ABCD中,,,且,则BC为( )
A.1 B. C. D.
9.如图,中,,将折叠,使点C与的中点D重合,折痕交于点M,交于点N,则线段的长为( ).
A. B. C.3 D.
10.如图,中,,一同学利用直尺和圆规完成如下操作:
①以点C为圆心,以CB为半径画弧,交AB于点G;分别以点G、B为圆心,以大于的长为半径画弧,两弧交点K,作射线CK;
②以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于N,分别以M、N为圆心,以大于的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E.
请你观察图形,根据操作结果解答下列问题;过点D作交AB的延长线于点F,若,,则CE的长为( )
A.13 B. C. D.
二、填空题
11.在Rt△ABC中,∠C=90°,且AC∶BC=1∶7,AB=100米,则AC=_________米.
12.如图,在△ABC中,AB=10,BC=9, AC=17,则BC边上的高为_______.
明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地……”翻译成现代文为:如图,秋千绳索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(AC=1尺).将它往前推进两步(EB⊥OC于点E,且EB=10尺),踏板升高到点B位置,此时踏板离地五尺(BD=CE=5尺),则秋千绳索(OA或OB)长______尺.
14.我国古代数学著作《九章算术》中的一个问题:一根竹子高 1 丈(1 丈=10 尺),折断后顶端落在离竹子底端 3 尺处,问折断处离地面的高度为多少尺?如图,设折断处离地面的高度为 x 尺,根据题意,可列出关于 x 方程为:__________.
15.如图,台风过后,某希望小学的旗杆在离地某处断裂,且旗杆顶部落在离旗杆底部8m处,已知旗杆原长16m,你能求出旗杆在离底部________m位置断裂.
16.如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则AE的长为__________cm.
《九章算术》中记载着这样一个问题:已知甲、乙两人同时从同一地点出发,甲的速度为7步/分,乙的速度为3步/分,乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇,那么相遇时,甲、乙各走了多远?解:如图,设甲乙两人出发后x分钟相遇.根据勾股定理可列得方程为______.
18.如图,的两直角边AC、BC的长分别为6、8,按图示那样折叠,使点A与点B重合,折痕为DE,则______.
19.如图,矩形ABCD中,AD=6,AB=8.点E为边DC上的一个动点,△AD'E与△ADE关于直线AE对称,当△CD'E为直角三角形时,DE的长为__.
三、解答题
20.如图,在一次地震中,一棵垂直于地面且高度为16米的大树被折断,树的顶部落在离树根8米处,即,求这棵树在离地面多高处被折断(即求AC的长度)?
21.如图,烟台市正政府决定在相距50km的A、B两村之间的公路旁E点,修建一个大樱桃批发市场,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么大樱桃批发市场E应建什么位置才能符合要求?
22.某海上有一小岛,为了测量小岛两端A,B的距离,测量人员设计了一种测量方法,如图,已知B是CD的中点,E是BA延长线上的一点,且∠CED=90°,测得AE=16.6海里,DE=60海里,CE=80海里.
(1) 求小岛两端A,B的距离.
(2) 过点C作CF⊥AB交AB的延长线于点F,求值.
23.如图,有一架秋千,当他静止时,踏板离地的垂直高度,将他往前推送(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
24.在△ABC中,,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为直角三角形时,求t的值.
已知m>0,若3m+2,4m+8,5m+8是一组勾股数,求m的值.
26.(1)图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.
(2)如果(1)中分割成的直角三角形两直角边分别为a,b斜边为c.请你利用图2中拼成的大正方形证明勾股定理.
(3)应用:测量旗杆的高度:校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度).
27.如图,某商家想在商场大楼上悬挂一块广告牌,广告牌高.根据商场规定广告牌最高点不得高于地面20m,经测量,测角仪支架高,在F处测得广告牌底部点B的仰角为30°,在E处测得标语牌顶部点A的仰角为45°,,请计算说明,商家这样放广告牌是否符合规定?(图中点A,B,C,D,E,F,G,H在同一平面内)
28.如图所示,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
(1) 出发3s后,求PQ的长;
(2) 当点Q在边BC上运动时,出发多久后,△PQB能形成等腰三角形?
(3) 当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
答案
一、单选题
1.C 2.A 3.C 4.A 5.C 6.A 7.C 8.B 9.D 10.D
二、填空题
11.
12.8
13.
14.
15.6
16.4
17.
18.
19.3或6
三、解答题
20.
设,利用勾股定理列方程求解即可.
解:设,
∵在中,,
∴,
∴.
答:这棵树在离地面6米处被折断
21.
解:设大樱桃批发市场E应建在离A站x千米的地方,则千米.
在直角中,根据勾股定理得:,
∴,
在直角中,根据勾股定理得:,
∴.
又∵C、D两村到E点的距离相等,
∴,
∴,
所以,
解得.
∴大樱桃批发市场E应建在离A站20千米的地方.
22.
解:(1)在△DCE中,∠CED=90°,DE=60海里,CE=80海里,
由勾股定理可得(海里),
∵B是CD的中点,
∴(海里),
∴AB=BE-AE=50-16.6=33.4(海里)
答:小岛两端A、B的距离是33.4海里;
(2)设BF=x海里.
在Rt△CFB中,∠CFB=90°,
∴CF2=CB2-BF2=502-x2=2500-x2,
在Rt△CFE中,∠CFE=90°,
∴CF2+EF2=CE2,即,
解得x=14,
∴
答:值为.
23.解:设秋千的绳索长为,则,
,
在中,
,即,
解得,
答:绳索的长度是.
24.解:在Rt△ABC中,由勾股定理得:,
∴BC=4cm,
由题意得:BP=tcm.,
①当∠APB为直角时,
如图①,点P与点C重合,
BP=BC=4cm,
∴t=4;
②当∠BAP为直角时,
如图②,BP=tcm.CP=(t-4)cm,AC=3cm,
在Rt△ACP中,,
在Rt△BAP中,,
即,
解得,
答:当△ABP为直角三角形时,t=4或.
25.
解: m>0, 3m+2,4m+8,5m+8是一组勾股数,
(3m+2)2+(4m+8)2=(5m+8)2,
解得:m=1.
26.
解:(1)如图
(2)
=
=
∴
(3)如图,在四边形ABCD中,AB⊥BC,DC⊥BC,AD比AB长0.5米,BC=4米,CD=0.5米,求AB的长.
解:过点D作DE⊥AB,垂足为E
∵ AB⊥BC,DC⊥BC
∴∠B=∠C=∠DEB=90
∴四边形BCDE是矩形
∴ED=BC=4,BE=DC=0.5
设AB=,则AD=+0.5,AE=-0.5
在RtΔAED中
AD2=AE2+ED2
(+0.5)2=(-0.5)2+42
解得:=8
答:旗杆的高为8米.
27.解:设
且
解得:
商家这样放广告牌不符合规定.
28.
解:(1)当t=3时,则AP=3,BQ=2t=6,
∵AB=16cm,
∴BP=AB﹣AP=16﹣3=13(cm),
在Rt△BPQ中,PQ===(cm).
(2)由题意可知AP=t,BQ=2t,
∵AB=16,
∴BP=AB﹣AP=16﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即16﹣t=2t,解得t=,
∴出发秒后△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则BE=,
∴CE===,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
