3.3方差和标准差 浙教版初中数学八年级下册同步练习(含解析)
文档属性
| 名称 | 3.3方差和标准差 浙教版初中数学八年级下册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 548.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
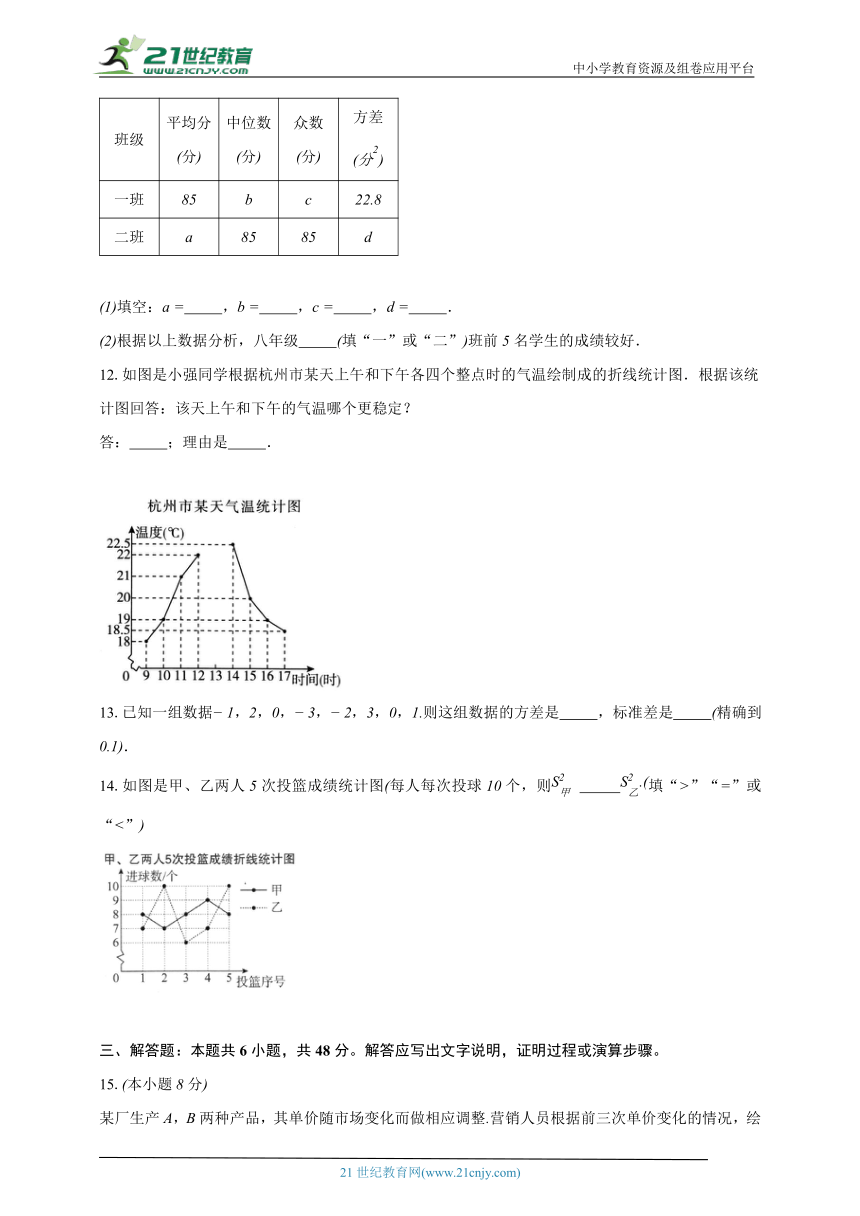
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.3方差和标准差浙教版初中数学八年级下册同步练习
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若数据,,,,,,的方差是,则数据,,,,,,的方差是
( )
A. B. C. D.
2.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续天,每天新增疑似病例不超过人”下列新增疑似病例的数据中,一定符合该标志的是( )
A. 平均数是,中位数是 B. 平均数是,总体方差是
C. 中位数是,众数是 D. 平均数是,方差大于
3.在对一组样本数据进行分析时,小华列出了方差的计算公式:
.
由公式提供的信息,得到以下四个结论:样本的容量是;样本的中位数是;样本的众数是;样本的平均数是其中正确的是
( )
A. B. C. D.
4.张阳把他和四位同学的年龄作为一组数据,计算出平均数是,方差是,则年后张阳等位同学的年龄的平均数和方差分别是( )
A. 和 B. 和 C. 和 D. 和
5.如果一组数据,,,的方差是,那么一组新数据,,,的方差是
( )
A. B. C. D.
6.一组数据:,,,,,若去掉一个数据,则下列统计量中发生变化的是( )
A. 众数 B. 中位数 C. 平均数 D. 方差
7.数据,,,,的方差是( )
A. B. C. D.
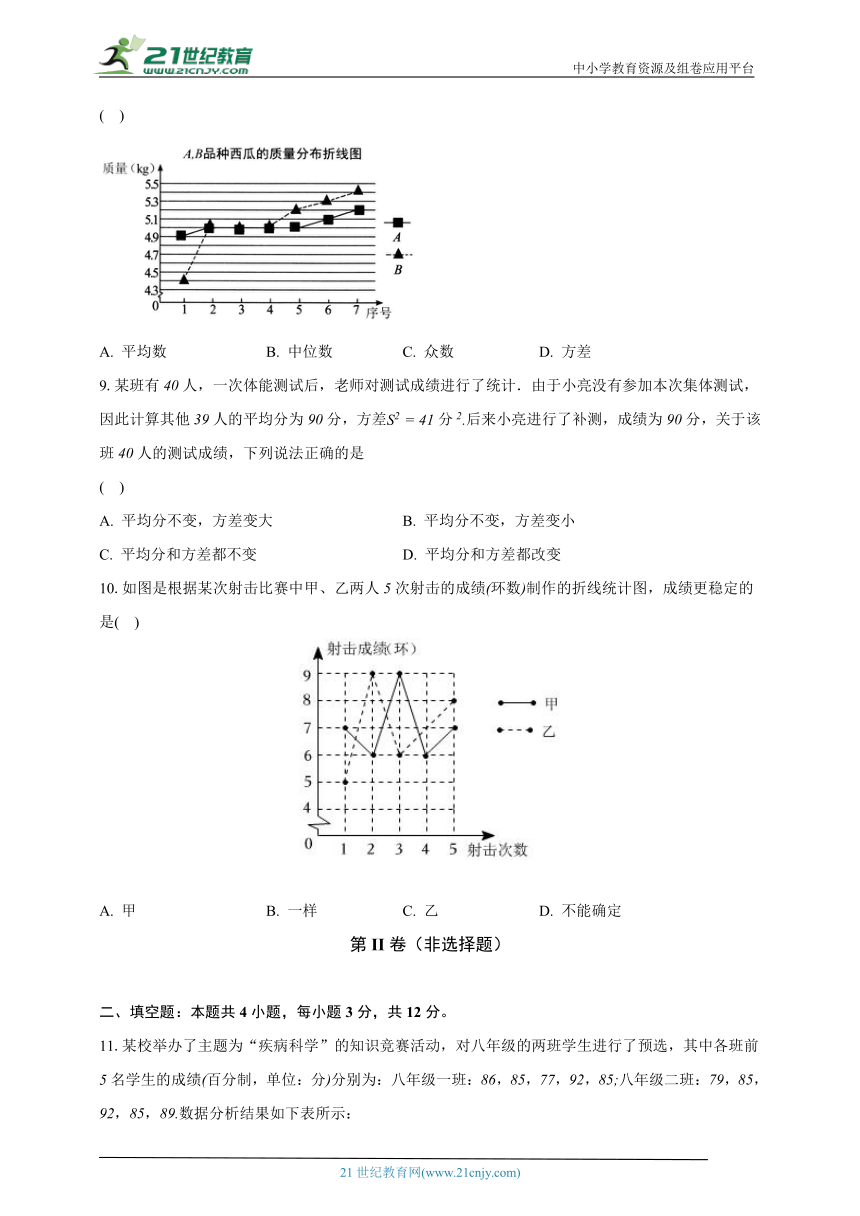
8.从,两个品种的西瓜中随机各取个,它们的质量分布折线图如图.下列统计量中,最能反映出这两组数据之间差异的是
( )
A. 平均数 B. 中位数 C. 众数 D. 方差
9.某班有人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他人的平均分为分,方差分后来小亮进行了补测,成绩为分,关于该班人的测试成绩,下列说法正确的是
( )
A. 平均分不变,方差变大 B. 平均分不变,方差变小
C. 平均分和方差都不变 D. 平均分和方差都改变
10.如图是根据某次射击比赛中甲、乙两人次射击的成绩环数制作的折线统计图,成绩更稳定的是( )
A. 甲 B. 一样 C. 乙 D. 不能确定
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
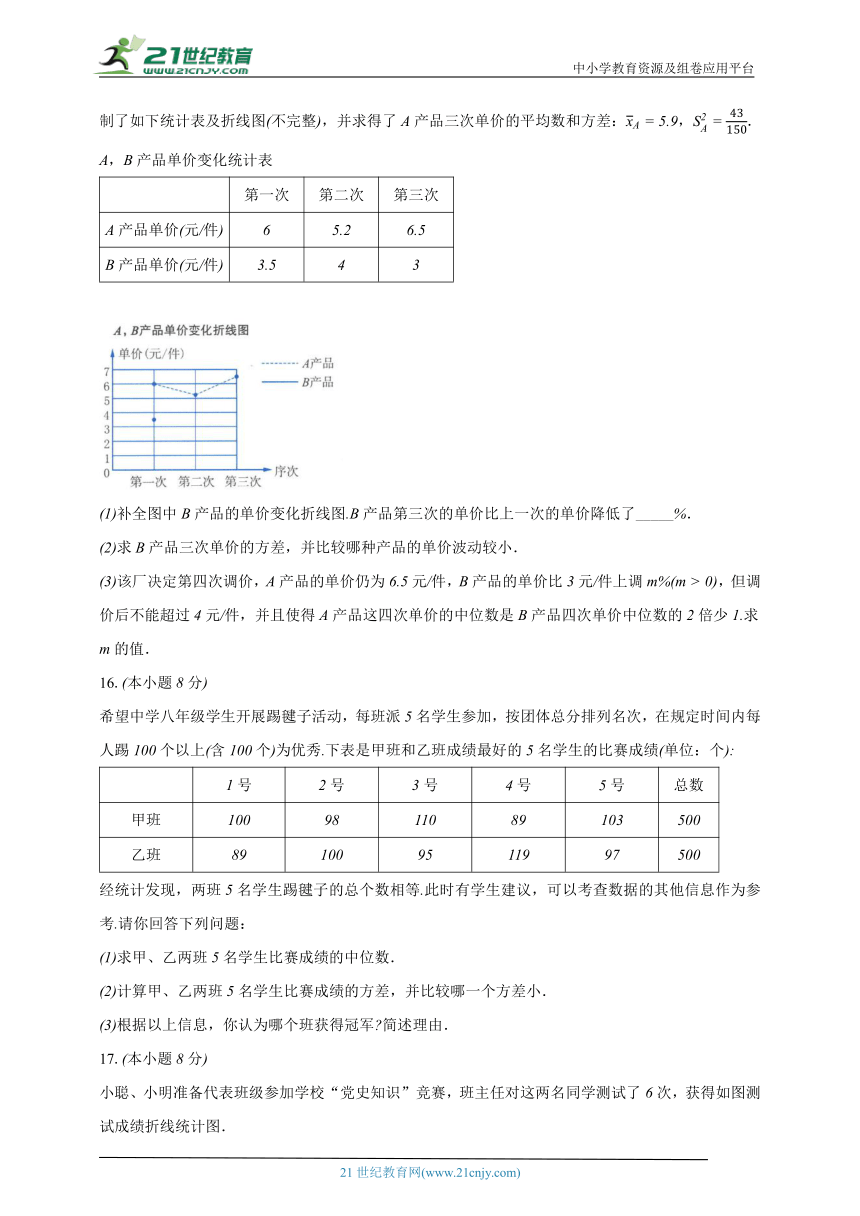
11.某校举办了主题为“疾病科学”的知识竞赛活动,对八年级的两班学生进行了预选,其中各班前名学生的成绩百分制,单位:分分别为:八年级一班:,,,,八年级二班:,,,,数据分析结果如下表所示:
班级 平均分
分 中位数
分 众数
分 方差
一班
二班
填空: , , , .
根据以上数据分析,八年级 填“一”或“二”班前名学生的成绩较好.
12.如图是小强同学根据杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图.根据该统计图回答:该天上午和下午的气温哪个更稳定?
答: ;理由是 .
13.已知一组数据,,,,,,,则这组数据的方差是 ,标准差是 精确到.
14.如图是甲、乙两人次投篮成绩统计图每人每次投球个,则 填“”“”或“”
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
某厂生产,两种产品,其单价随市场变化而做相应调整营销人员根据前三次单价变化的情况,绘制了如下统计表及折线图不完整,并求得了产品三次单价的平均数和方差:,.
,产品单价变化统计表
第一次 第二次 第三次
产品单价元件
产品单价元件
补全图中产品的单价变化折线图产品第三次的单价比上一次的单价降低了_____.
求产品三次单价的方差,并比较哪种产品的单价波动较小.
该厂决定第四次调价,产品的单价仍为元件,产品的单价比元件上调,但调价后不能超过元件,并且使得产品这四次单价的中位数是产品四次单价中位数的倍少求的值.
16.本小题分
希望中学八年级学生开展踢毽子活动,每班派名学生参加,按团体总分排列名次,在规定时间内每人踢个以上含个为优秀下表是甲班和乙班成绩最好的名学生的比赛成绩单位:个
号 号 号 号 号 总数
甲班
乙班
经统计发现,两班名学生踢毽子的总个数相等此时有学生建议,可以考查数据的其他信息作为参考请你回答下列问题:
求甲、乙两班名学生比赛成绩的中位数.
计算甲、乙两班名学生比赛成绩的方差,并比较哪一个方差小.
根据以上信息,你认为哪个班获得冠军简述理由.
17.本小题分
小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了次,获得如图测试成绩折线统计图.
根据图中信息,解答下列问题:
要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.
求小聪成绩的方差.
现求得小明成绩的方差为单位:平方分根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.
18.本小题分
某旅游景区上山的一条小路上有一些断断续续的台阶下图是其中甲、乙两段台阶路的示意图,图中的数字表示各级台阶的高度,数据,,,,,的方差.
哪段台阶路走起来舒服些为什么
为方便游客行走,需对这两段台阶路进行整修在保持台阶数不变的情况下,请你提出合理的整修建议.
19.本小题分
某旅游景区上山的一条小路上有一些断断续续的台阶下图是其中甲、乙两段台阶路的示意图,图中的数字表示各级台阶的高度,数据,,,,,的方差.
哪段台阶路走起来舒服些为什么
为方便游客行走,需对这两段台阶路进行整修在保持台阶数不变的情况下,请你提出合理的整修建议.
20.本小题分
八年级选派甲、乙两组各名同学参加数学抢答比赛共有道选择题,答对题以上含题为优秀各组选手答对题数统计如表根据表的数据,填写表.
表
答对题数
甲组
乙组
表
平均数 中位数 众数 方差 优秀率
甲组
乙组
请你完成上表,并根据你所学的统计学知识,从不同方面评价甲、乙两组选手的成绩.
答案和解析
1.【答案】
【解析】【分析】
本题考查方差的计算公式的运用:一般地设有个数据,,,,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.根据如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的波动情况不变,即方差不变,从而得出答案.
【解答】
解:一组数据中的每一个数据都加上或都减去同一个常数后,它的平均数都加上或都减去这一个常数,两数进行相减,故方差不变,
一组数据中的每一个数据都乘以或都除以同一个常数后,它的平均数都乘以或都除以这一个常数,两数进行相减,故方差成平方变化,
,,,,,,是在原数据,,,,,,中每个数均先乘以再加上,
数据,,,,,,的方差为数据,,,,,,的方差的倍.
故选D.
2.【答案】
【解析】平均数、中位数和众数不能说明某天新增疑似病例是否超过人,故A,C错误.
设连续天,每天新增疑似病例为,,,,,若有一天新增疑似病例超过人,假设为人,则,若方差是,说明连续天,每天新增疑似病例不超过人,故B正确.
当方差大于,方差的具体数值未知,不能确定数据的波动大小,故D错误.
故选B.
3.【答案】
【解析】略
4.【答案】
【解析】【分析】
本题考查方差的定义问题,可以推广到一般的情况即样本中如果每个数据都加上一个数,则平均值为,方差不变;
如果样本中每个数据都乘以一个数,这平均值为,方差为可分别计算前后的方差作比较;也可根据方差是反映数据波动大小的量来判断.
【解答】
解:设张阳及其他四名同学的年龄分别为,,,,,平均年龄,
方差,
十年后五名同学的年龄分别为,,,,,
平均年龄为;
方差
,故ABD错误,C正确.
故选C.
5.【答案】
【解析】【分析】
本题考查了方差,设一组数据,,,的平均数为,方差是,则另一组数据,,,的平均数为,方差是,代入方差的公式,计算即可.
【解答】
解:设一组数据,,,的平均数为,方差是,则另一组数据,,,的平均数为,方差是,
,
.
故选:.
6.【答案】
【解析】解:由题意得:原中位数为,原众数为,原平均数为,原方差为;
去掉一个数据后的中位数为,众数为,平均数为,方差为;
统计量发生变化的是方差.
故选:.
依据平均数、中位数、众数、方差的定义和公式分别进行求解即可.
本题主要考查平均数、众数、众数及方差,熟练掌握求一组数据的平均数、众数及方差是解题的关键.
7.【答案】
【解析】【分析】
此题主要考查了方差的有关知识,正确的求出平均数,并正确代入方差公式是解决问题的关键.结合方差公式先求出这组数据的平均数,然后代入方差公式计算即可.
【解答】
解:平均数为:,
,
,
.
8.【答案】
【解析】解:由图可得,
,
,
故反映出这两组数据之间差异不能反映出这两组数据之间差异,故选项A不符合题意;
和的中位数和众数都相等,故不能反映出这两组数据之间差异,故选项B和不符合题意;
由图象可得,种数据波动小,比较稳定,种数据波动大,不稳定,能反映出这两组数据之间差异,故选项D符合题意;
故选:.
根据统计图中的数据,可以判断哪个选项符合题意,本题得以解决.
本题考查折线统计图、中位数、众数、平均数、方差,解答本题的关键是明确题意,利用数形结合的思想解答.
9.【答案】
【解析】【分析】
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
根据平均数,方差的定义计算即可.
【解答】
解:小亮的成绩和其他人的平均数相同,都是分,
该班人的测试成绩的平均分为分,平均分不变,
人数多了一人,平均分不变,则方差变小,
故选B.
10.【答案】
【解析】解:甲的平均成绩为,
乙的平均成绩为,
甲成绩的方差为,
乙成绩的方差为,
,
甲的成绩更稳定.
故选:.
方差小的较稳定,分别求出甲、乙方差,即可得到答案.
本题考查了方差的应用,掌握方差的定义是关键.
11.【答案】【小题】
【小题】
二
【解析】 略
略
12.【答案】下午
上午的气温的方差大于下午的气温的方差
【解析】略
13.【答案】
【解析】略
14.【答案】
【解析】略
15.【答案】【小题】略
【小题】略
【小题】略
【解析】 略
略
略
16.【答案】【小题】略
【小题】略
【小题】略
【解析】 略
略
略
17.【答案】解:要评价每位同学成绩的平均水平,选择平均数即可,
小聪成绩的平均数:分,
小明成绩的平均数:分,
答:应选择平均数,小聪、小明的平均数分别是分,分;
小聪成绩的方差为:;
小聪同学的成绩较好,
理由:由可知两人的平均数相同,因为小聪成绩的方差小于小明成绩的方差,成绩相对稳定.
故小聪同学的成绩较好.
【解析】本题考查平均数、方差,折线统计图,解答本题的关键是明确题意,找出所求问题需要的条件,会计算一组数据的平均数和方差.
要评价每位同学成绩的平均水平,选择平均数即可,根据平均数的定义计算出两人的平均数即可;
根据方差的计算方法计算即可;
由可知两人的平均数相同,由方差可知小聪的成绩波动较小,所以方差较小,成绩相对稳定.
18.【答案】【小题】略
【小题】略
【解析】 略
略
19.【答案】略
【解析】略
20.【答案】略
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.3方差和标准差浙教版初中数学八年级下册同步练习
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若数据,,,,,,的方差是,则数据,,,,,,的方差是
( )
A. B. C. D.
2.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续天,每天新增疑似病例不超过人”下列新增疑似病例的数据中,一定符合该标志的是( )
A. 平均数是,中位数是 B. 平均数是,总体方差是
C. 中位数是,众数是 D. 平均数是,方差大于
3.在对一组样本数据进行分析时,小华列出了方差的计算公式:
.
由公式提供的信息,得到以下四个结论:样本的容量是;样本的中位数是;样本的众数是;样本的平均数是其中正确的是
( )
A. B. C. D.
4.张阳把他和四位同学的年龄作为一组数据,计算出平均数是,方差是,则年后张阳等位同学的年龄的平均数和方差分别是( )
A. 和 B. 和 C. 和 D. 和
5.如果一组数据,,,的方差是,那么一组新数据,,,的方差是
( )
A. B. C. D.
6.一组数据:,,,,,若去掉一个数据,则下列统计量中发生变化的是( )
A. 众数 B. 中位数 C. 平均数 D. 方差
7.数据,,,,的方差是( )
A. B. C. D.
8.从,两个品种的西瓜中随机各取个,它们的质量分布折线图如图.下列统计量中,最能反映出这两组数据之间差异的是
( )
A. 平均数 B. 中位数 C. 众数 D. 方差
9.某班有人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他人的平均分为分,方差分后来小亮进行了补测,成绩为分,关于该班人的测试成绩,下列说法正确的是
( )
A. 平均分不变,方差变大 B. 平均分不变,方差变小
C. 平均分和方差都不变 D. 平均分和方差都改变
10.如图是根据某次射击比赛中甲、乙两人次射击的成绩环数制作的折线统计图,成绩更稳定的是( )
A. 甲 B. 一样 C. 乙 D. 不能确定
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
11.某校举办了主题为“疾病科学”的知识竞赛活动,对八年级的两班学生进行了预选,其中各班前名学生的成绩百分制,单位:分分别为:八年级一班:,,,,八年级二班:,,,,数据分析结果如下表所示:
班级 平均分
分 中位数
分 众数
分 方差
一班
二班
填空: , , , .
根据以上数据分析,八年级 填“一”或“二”班前名学生的成绩较好.
12.如图是小强同学根据杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图.根据该统计图回答:该天上午和下午的气温哪个更稳定?
答: ;理由是 .
13.已知一组数据,,,,,,,则这组数据的方差是 ,标准差是 精确到.
14.如图是甲、乙两人次投篮成绩统计图每人每次投球个,则 填“”“”或“”
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
某厂生产,两种产品,其单价随市场变化而做相应调整营销人员根据前三次单价变化的情况,绘制了如下统计表及折线图不完整,并求得了产品三次单价的平均数和方差:,.
,产品单价变化统计表
第一次 第二次 第三次
产品单价元件
产品单价元件
补全图中产品的单价变化折线图产品第三次的单价比上一次的单价降低了_____.
求产品三次单价的方差,并比较哪种产品的单价波动较小.
该厂决定第四次调价,产品的单价仍为元件,产品的单价比元件上调,但调价后不能超过元件,并且使得产品这四次单价的中位数是产品四次单价中位数的倍少求的值.
16.本小题分
希望中学八年级学生开展踢毽子活动,每班派名学生参加,按团体总分排列名次,在规定时间内每人踢个以上含个为优秀下表是甲班和乙班成绩最好的名学生的比赛成绩单位:个
号 号 号 号 号 总数
甲班
乙班
经统计发现,两班名学生踢毽子的总个数相等此时有学生建议,可以考查数据的其他信息作为参考请你回答下列问题:
求甲、乙两班名学生比赛成绩的中位数.
计算甲、乙两班名学生比赛成绩的方差,并比较哪一个方差小.
根据以上信息,你认为哪个班获得冠军简述理由.
17.本小题分
小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了次,获得如图测试成绩折线统计图.
根据图中信息,解答下列问题:
要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.
求小聪成绩的方差.
现求得小明成绩的方差为单位:平方分根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.
18.本小题分
某旅游景区上山的一条小路上有一些断断续续的台阶下图是其中甲、乙两段台阶路的示意图,图中的数字表示各级台阶的高度,数据,,,,,的方差.
哪段台阶路走起来舒服些为什么
为方便游客行走,需对这两段台阶路进行整修在保持台阶数不变的情况下,请你提出合理的整修建议.
19.本小题分
某旅游景区上山的一条小路上有一些断断续续的台阶下图是其中甲、乙两段台阶路的示意图,图中的数字表示各级台阶的高度,数据,,,,,的方差.
哪段台阶路走起来舒服些为什么
为方便游客行走,需对这两段台阶路进行整修在保持台阶数不变的情况下,请你提出合理的整修建议.
20.本小题分
八年级选派甲、乙两组各名同学参加数学抢答比赛共有道选择题,答对题以上含题为优秀各组选手答对题数统计如表根据表的数据,填写表.
表
答对题数
甲组
乙组
表
平均数 中位数 众数 方差 优秀率
甲组
乙组
请你完成上表,并根据你所学的统计学知识,从不同方面评价甲、乙两组选手的成绩.
答案和解析
1.【答案】
【解析】【分析】
本题考查方差的计算公式的运用:一般地设有个数据,,,,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.根据如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的波动情况不变,即方差不变,从而得出答案.
【解答】
解:一组数据中的每一个数据都加上或都减去同一个常数后,它的平均数都加上或都减去这一个常数,两数进行相减,故方差不变,
一组数据中的每一个数据都乘以或都除以同一个常数后,它的平均数都乘以或都除以这一个常数,两数进行相减,故方差成平方变化,
,,,,,,是在原数据,,,,,,中每个数均先乘以再加上,
数据,,,,,,的方差为数据,,,,,,的方差的倍.
故选D.
2.【答案】
【解析】平均数、中位数和众数不能说明某天新增疑似病例是否超过人,故A,C错误.
设连续天,每天新增疑似病例为,,,,,若有一天新增疑似病例超过人,假设为人,则,若方差是,说明连续天,每天新增疑似病例不超过人,故B正确.
当方差大于,方差的具体数值未知,不能确定数据的波动大小,故D错误.
故选B.
3.【答案】
【解析】略
4.【答案】
【解析】【分析】
本题考查方差的定义问题,可以推广到一般的情况即样本中如果每个数据都加上一个数,则平均值为,方差不变;
如果样本中每个数据都乘以一个数,这平均值为,方差为可分别计算前后的方差作比较;也可根据方差是反映数据波动大小的量来判断.
【解答】
解:设张阳及其他四名同学的年龄分别为,,,,,平均年龄,
方差,
十年后五名同学的年龄分别为,,,,,
平均年龄为;
方差
,故ABD错误,C正确.
故选C.
5.【答案】
【解析】【分析】
本题考查了方差,设一组数据,,,的平均数为,方差是,则另一组数据,,,的平均数为,方差是,代入方差的公式,计算即可.
【解答】
解:设一组数据,,,的平均数为,方差是,则另一组数据,,,的平均数为,方差是,
,
.
故选:.
6.【答案】
【解析】解:由题意得:原中位数为,原众数为,原平均数为,原方差为;
去掉一个数据后的中位数为,众数为,平均数为,方差为;
统计量发生变化的是方差.
故选:.
依据平均数、中位数、众数、方差的定义和公式分别进行求解即可.
本题主要考查平均数、众数、众数及方差,熟练掌握求一组数据的平均数、众数及方差是解题的关键.
7.【答案】
【解析】【分析】
此题主要考查了方差的有关知识,正确的求出平均数,并正确代入方差公式是解决问题的关键.结合方差公式先求出这组数据的平均数,然后代入方差公式计算即可.
【解答】
解:平均数为:,
,
,
.
8.【答案】
【解析】解:由图可得,
,
,
故反映出这两组数据之间差异不能反映出这两组数据之间差异,故选项A不符合题意;
和的中位数和众数都相等,故不能反映出这两组数据之间差异,故选项B和不符合题意;
由图象可得,种数据波动小,比较稳定,种数据波动大,不稳定,能反映出这两组数据之间差异,故选项D符合题意;
故选:.
根据统计图中的数据,可以判断哪个选项符合题意,本题得以解决.
本题考查折线统计图、中位数、众数、平均数、方差,解答本题的关键是明确题意,利用数形结合的思想解答.
9.【答案】
【解析】【分析】
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
根据平均数,方差的定义计算即可.
【解答】
解:小亮的成绩和其他人的平均数相同,都是分,
该班人的测试成绩的平均分为分,平均分不变,
人数多了一人,平均分不变,则方差变小,
故选B.
10.【答案】
【解析】解:甲的平均成绩为,
乙的平均成绩为,
甲成绩的方差为,
乙成绩的方差为,
,
甲的成绩更稳定.
故选:.
方差小的较稳定,分别求出甲、乙方差,即可得到答案.
本题考查了方差的应用,掌握方差的定义是关键.
11.【答案】【小题】
【小题】
二
【解析】 略
略
12.【答案】下午
上午的气温的方差大于下午的气温的方差
【解析】略
13.【答案】
【解析】略
14.【答案】
【解析】略
15.【答案】【小题】略
【小题】略
【小题】略
【解析】 略
略
略
16.【答案】【小题】略
【小题】略
【小题】略
【解析】 略
略
略
17.【答案】解:要评价每位同学成绩的平均水平,选择平均数即可,
小聪成绩的平均数:分,
小明成绩的平均数:分,
答:应选择平均数,小聪、小明的平均数分别是分,分;
小聪成绩的方差为:;
小聪同学的成绩较好,
理由:由可知两人的平均数相同,因为小聪成绩的方差小于小明成绩的方差,成绩相对稳定.
故小聪同学的成绩较好.
【解析】本题考查平均数、方差,折线统计图,解答本题的关键是明确题意,找出所求问题需要的条件,会计算一组数据的平均数和方差.
要评价每位同学成绩的平均水平,选择平均数即可,根据平均数的定义计算出两人的平均数即可;
根据方差的计算方法计算即可;
由可知两人的平均数相同,由方差可知小聪的成绩波动较小,所以方差较小,成绩相对稳定.
18.【答案】【小题】略
【小题】略
【解析】 略
略
19.【答案】略
【解析】略
20.【答案】略
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
