浙教版八年级数学上册试题 第5章 一次函数 全章复习与巩固(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 第5章 一次函数 全章复习与巩固(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 345.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 10:32:05 | ||
图片预览


文档简介
《一次函数》全章复习与巩固
一、单选题
1.若函数是一次函数,则应满足( )
A. B. C. D.
2.下列各图像中, y 不是 x 的函数有( )
A.B.C. D.
3.已知正比例函数y=3x的图象经过点(1,m),则m的值为( )
A. B.3 C.﹣ D.﹣3
4.在平面直角坐标系中,将函数的图象向左平移个单位长度,则平移后的图象与轴的交点坐标为( )
A. B. C. D.
5.已知函数,y随x的增大而减小,则一次函数的图象经过( )
A.一,二,三象限 B.一,二,四象限
C.一,三,四象限 D.二,三,四象限
6.一次函数的图象过点,,,则( )
A. B. C. D.
7.如图,一次函数的图象经过点,则下列说法正确的是( )
A. B.
C.方程的解是 D.随的增大而减小
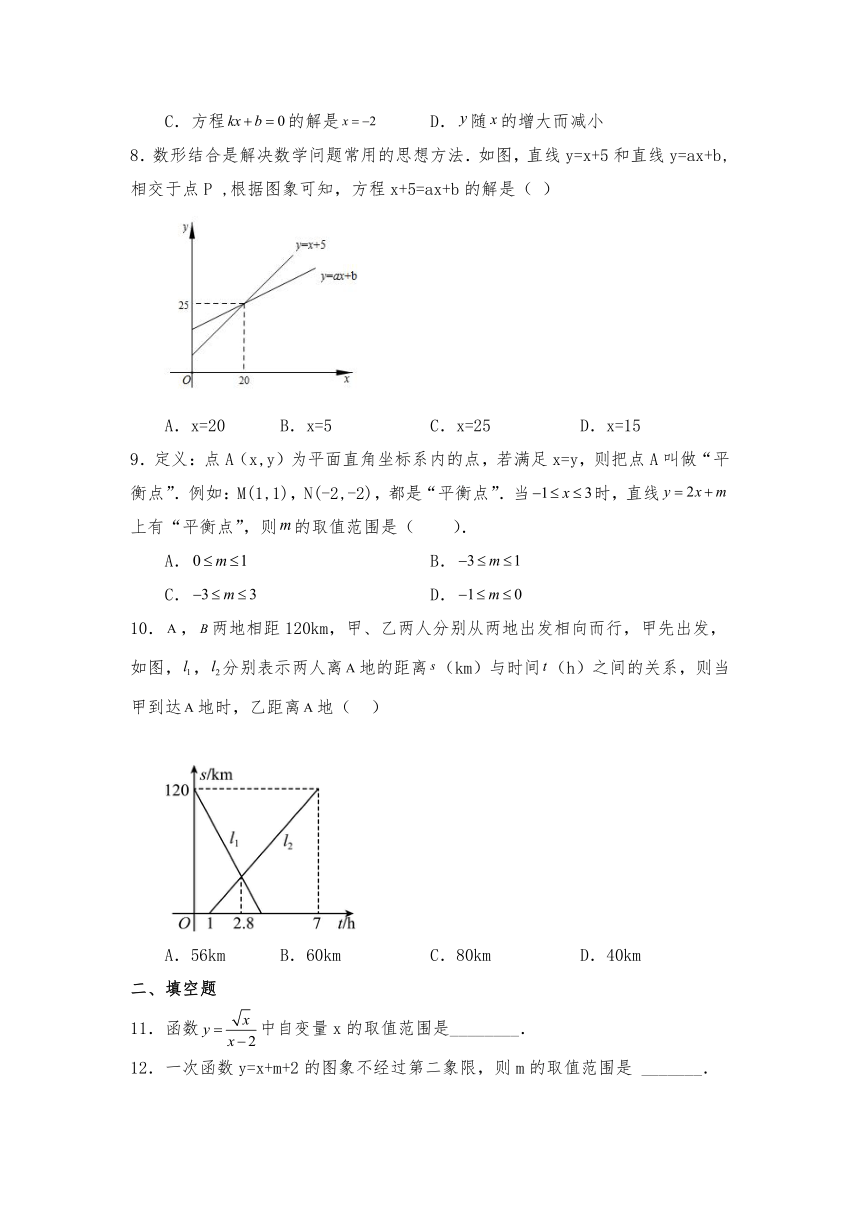
8.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
9.定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(-2,-2),都是“平衡点”.当时,直线上有“平衡点”,则的取值范围是( ).
A. B.
C. D.
10.,两地相距120km,甲、乙两人分别从两地出发相向而行,甲先出发,如图,,分别表示两人离地的距离(km)与时间(h)之间的关系,则当甲到达地时,乙距离地( )
A.56km B.60km C.80km D.40km
二、填空题
11.函数中自变量x的取值范围是________.
12.一次函数y=x+m+2的图象不经过第二象限,则m的取值范围是 _______.
13.若一次函数的图象经过第一、二、四象限,则化简________.
14.若一次函数的函数值y随x的增大而减小,则k的取值范围是______.
15.已知一次函数y=kx+b,且当-3≤x≤1时,1≤y≤9,则k+b的值为_____________
16.如图,平面直角坐标系中,经过点B(﹣4,0)的直线y=kx+b与直线y=mx+2相交于点,则关于x的方程mx+2=kx+b的解为________.
17.已知一次函数的图象经过点,与x轴的交点为B,若,则这个一次函数的解析式为______.
18.如图,把放在平面直角坐标系内,其中,,点,的坐标分别为,,将沿轴向右平移,当点落在直线上时,线段扫过的面积为______.
19.点P为直线上的任意一点,O为原点,则的最小值为_________.
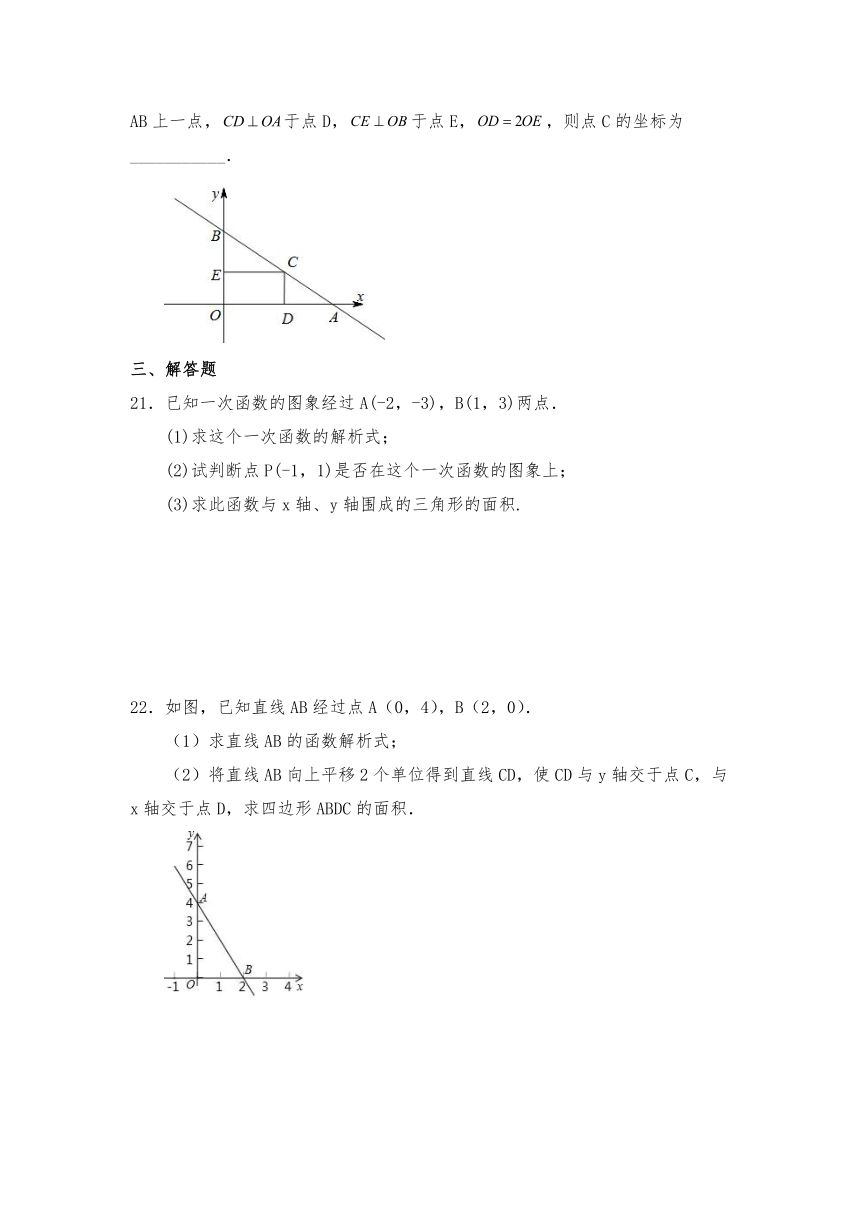
20.如图,一次函数的图象与x轴,y轴分别交于A,B两点.C是线段AB上一点,于点D,于点E,,则点C的坐标为___________.
三、解答题
21.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
22.如图,已知直线AB经过点A(0,4),B(2,0).
(1)求直线AB的函数解析式;
(2)将直线AB向上平移2个单位得到直线CD,使CD与y轴交于点C,与x轴交于点D,求四边形ABDC的面积.
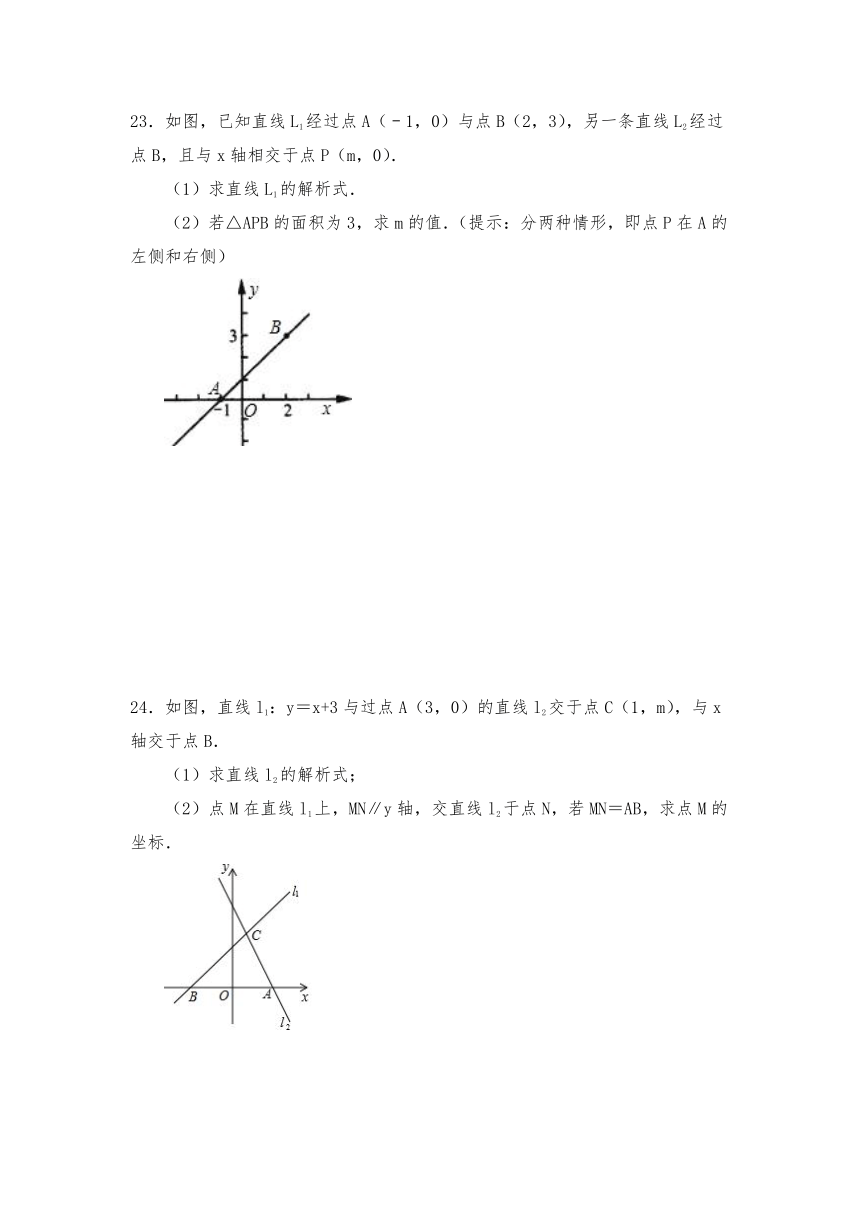
23.如图,已知直线L1经过点A(﹣1,0)与点B(2,3),另一条直线L2经过点B,且与x轴相交于点P(m,0).
(1)求直线L1的解析式.
(2)若△APB的面积为3,求m的值.(提示:分两种情形,即点P在A的左侧和右侧)
24.如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
25.为了做好新冠防疫工作,某学校开学前备足防疫物资,准备体温枪和消毒液若干,经市场调查:购买一把体温枪20元,一瓶消毒液5元,市场上现有甲,乙两所医疗机构.甲医疗机构销售方案为:购买一把体温枪送一瓶消毒液.乙医疗机构销售方案为:购买体温枪和消毒液全部打九折.若某学校准备购买50把体温枪,购买消毒液瓶().
(1)分别写出按甲医疗机构销售方案购买费用(元)、按乙医疗机构销售方案购买费用(元)与购买消毒液(瓶)之间的函数关系式;
(2)当时,甲、乙两家医疗机构哪家购买费用比较合算.
26.如图,已知点A(6,4),直线l1经过点B(0,2)、点C(3, 3),且与x轴交于点D,连接AD、AC,AC与x轴交于点P.
(1) 求直线l1的表达式,并求出点D的坐标;
(2) 在线段AD上存在一点Q.使S△PDQ=S△PDC,请求出点Q的坐标;
(3) 一次函数y=kx+k+5的图象为l2,若点A,D到l2的图象的距离相等,直接写出k的值.
答案
一、单选题
1.C 2.D 3.B 4.C 5.B 6.B 7.C 8.A 9.B 10.B
二、填空题
11.且
12.m≤-2
13.
14.
15.9或1
16.
17.或
18.16
19.
20.
三、解答题
21.解:
(1)设一次函数的表达式为y=kx+b,
则-3=-2k+b、3=k+b,解得:k=2,b=1.
∴函数的解析式为:y=2x+1.
(2)将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
(3)当x=0,y=1,当y=0,x=,
此函数与x轴、y轴围成的三角形的面积为:
22.解:(1)设直线AB的函数解析式为y=kx+b,依题意有
,
解得.
故直线AB的函数解析式为y=﹣2x+4;
(2)四边形ABDC的面积
=三角形COD的面积﹣三角形AOB的面积
=(4+2)×(2+1)÷2﹣4×2÷2
=9﹣4
=5.
故四边形ABDC的面积是5.
23.
解:(1)设直线L1的解析式为y=kx+b,
∵直线L1经过点A(﹣1,0)与点B(2,3),
∴,
解得.
所以直线L1的解析式为y=x+1.
(2)当点P在点A的右侧时,AP=m﹣(﹣1)=m+1,有S△APB=×(m+1)×3=3,
解得:m=1.此时点P的坐标为(1,0).
当点P在点A的左侧时,AP=﹣1﹣m,有S△APB=×|﹣m﹣1|×3=3,解得:m=﹣3,
此时,点P的坐标为(﹣3,0).
综上所述,m的值为1或﹣3.
24.
解:(1)在y=x+3中,令y=0,得x=﹣3,
∴B(﹣3,0),
把x=1代入y=x+3得y=4,
∴C(1,4),
设直线l2的解析式为y=kx+b,
∴,解得,
∴直线l2的解析式为y=﹣2x+6;
(2)AB=3﹣(﹣3)=6,
设M(a,a+3),由MN∥y轴,得N(a,﹣2a+6),
MN=|a+3﹣(﹣2a+6)|=AB=6,
解得a=3或a=﹣1,
∴M(3,6)或(﹣1,2).
25.
解:(1)由题意,从甲医疗机构购买一把体温枪,送一瓶消毒液,则
∴时,只需购买体温枪;时,需要买瓶消毒液;
∵,
∴;
从乙医疗机构购买全部打九折,
∴;
当时,
甲:(元);
乙:(元),
∵,
∴当时,从甲家医疗机构购买费用比较合算.
26.
(1)解:设l1的表达式为y=kx+b(k≠0),
∵l1经过点B(0,2)、点C(3, 3),
∴,解得,
∴l1的函数表达式:y=x+2.
∵点D为l1与x轴的交点,
故令y=0,x+2=0,
解得x=,
∴点D坐标为,0);
(2)解:由(1)同理可得AD所在直线的一次函数表达式为:,
∵点Q在线段上,
∴设点Q坐标为,其中.
∵,
∴,即,
解得,满足题意.
∴点Q坐标为;
(3)解:∵y=kx+k+5=(k+1)x+5,
∴直线l2过定点(-1,5),
∵点A,D到l2的图像的距离相等,
∴当l2与线段AD平行或过线段AD中点,
当l2与线段AD平行时,k=;
当l2过线段AD中点(,2)时,
∴2=k+k+5,
解得:k=;
综上,k的值为或.
一、单选题
1.若函数是一次函数,则应满足( )
A. B. C. D.
2.下列各图像中, y 不是 x 的函数有( )
A.B.C. D.
3.已知正比例函数y=3x的图象经过点(1,m),则m的值为( )
A. B.3 C.﹣ D.﹣3
4.在平面直角坐标系中,将函数的图象向左平移个单位长度,则平移后的图象与轴的交点坐标为( )
A. B. C. D.
5.已知函数,y随x的增大而减小,则一次函数的图象经过( )
A.一,二,三象限 B.一,二,四象限
C.一,三,四象限 D.二,三,四象限
6.一次函数的图象过点,,,则( )
A. B. C. D.
7.如图,一次函数的图象经过点,则下列说法正确的是( )
A. B.
C.方程的解是 D.随的增大而减小
8.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
9.定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(-2,-2),都是“平衡点”.当时,直线上有“平衡点”,则的取值范围是( ).
A. B.
C. D.
10.,两地相距120km,甲、乙两人分别从两地出发相向而行,甲先出发,如图,,分别表示两人离地的距离(km)与时间(h)之间的关系,则当甲到达地时,乙距离地( )
A.56km B.60km C.80km D.40km
二、填空题
11.函数中自变量x的取值范围是________.
12.一次函数y=x+m+2的图象不经过第二象限,则m的取值范围是 _______.
13.若一次函数的图象经过第一、二、四象限,则化简________.
14.若一次函数的函数值y随x的增大而减小,则k的取值范围是______.
15.已知一次函数y=kx+b,且当-3≤x≤1时,1≤y≤9,则k+b的值为_____________
16.如图,平面直角坐标系中,经过点B(﹣4,0)的直线y=kx+b与直线y=mx+2相交于点,则关于x的方程mx+2=kx+b的解为________.
17.已知一次函数的图象经过点,与x轴的交点为B,若,则这个一次函数的解析式为______.
18.如图,把放在平面直角坐标系内,其中,,点,的坐标分别为,,将沿轴向右平移,当点落在直线上时,线段扫过的面积为______.
19.点P为直线上的任意一点,O为原点,则的最小值为_________.
20.如图,一次函数的图象与x轴,y轴分别交于A,B两点.C是线段AB上一点,于点D,于点E,,则点C的坐标为___________.
三、解答题
21.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上;
(3)求此函数与x轴、y轴围成的三角形的面积.
22.如图,已知直线AB经过点A(0,4),B(2,0).
(1)求直线AB的函数解析式;
(2)将直线AB向上平移2个单位得到直线CD,使CD与y轴交于点C,与x轴交于点D,求四边形ABDC的面积.
23.如图,已知直线L1经过点A(﹣1,0)与点B(2,3),另一条直线L2经过点B,且与x轴相交于点P(m,0).
(1)求直线L1的解析式.
(2)若△APB的面积为3,求m的值.(提示:分两种情形,即点P在A的左侧和右侧)
24.如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
25.为了做好新冠防疫工作,某学校开学前备足防疫物资,准备体温枪和消毒液若干,经市场调查:购买一把体温枪20元,一瓶消毒液5元,市场上现有甲,乙两所医疗机构.甲医疗机构销售方案为:购买一把体温枪送一瓶消毒液.乙医疗机构销售方案为:购买体温枪和消毒液全部打九折.若某学校准备购买50把体温枪,购买消毒液瓶().
(1)分别写出按甲医疗机构销售方案购买费用(元)、按乙医疗机构销售方案购买费用(元)与购买消毒液(瓶)之间的函数关系式;
(2)当时,甲、乙两家医疗机构哪家购买费用比较合算.
26.如图,已知点A(6,4),直线l1经过点B(0,2)、点C(3, 3),且与x轴交于点D,连接AD、AC,AC与x轴交于点P.
(1) 求直线l1的表达式,并求出点D的坐标;
(2) 在线段AD上存在一点Q.使S△PDQ=S△PDC,请求出点Q的坐标;
(3) 一次函数y=kx+k+5的图象为l2,若点A,D到l2的图象的距离相等,直接写出k的值.
答案
一、单选题
1.C 2.D 3.B 4.C 5.B 6.B 7.C 8.A 9.B 10.B
二、填空题
11.且
12.m≤-2
13.
14.
15.9或1
16.
17.或
18.16
19.
20.
三、解答题
21.解:
(1)设一次函数的表达式为y=kx+b,
则-3=-2k+b、3=k+b,解得:k=2,b=1.
∴函数的解析式为:y=2x+1.
(2)将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
(3)当x=0,y=1,当y=0,x=,
此函数与x轴、y轴围成的三角形的面积为:
22.解:(1)设直线AB的函数解析式为y=kx+b,依题意有
,
解得.
故直线AB的函数解析式为y=﹣2x+4;
(2)四边形ABDC的面积
=三角形COD的面积﹣三角形AOB的面积
=(4+2)×(2+1)÷2﹣4×2÷2
=9﹣4
=5.
故四边形ABDC的面积是5.
23.
解:(1)设直线L1的解析式为y=kx+b,
∵直线L1经过点A(﹣1,0)与点B(2,3),
∴,
解得.
所以直线L1的解析式为y=x+1.
(2)当点P在点A的右侧时,AP=m﹣(﹣1)=m+1,有S△APB=×(m+1)×3=3,
解得:m=1.此时点P的坐标为(1,0).
当点P在点A的左侧时,AP=﹣1﹣m,有S△APB=×|﹣m﹣1|×3=3,解得:m=﹣3,
此时,点P的坐标为(﹣3,0).
综上所述,m的值为1或﹣3.
24.
解:(1)在y=x+3中,令y=0,得x=﹣3,
∴B(﹣3,0),
把x=1代入y=x+3得y=4,
∴C(1,4),
设直线l2的解析式为y=kx+b,
∴,解得,
∴直线l2的解析式为y=﹣2x+6;
(2)AB=3﹣(﹣3)=6,
设M(a,a+3),由MN∥y轴,得N(a,﹣2a+6),
MN=|a+3﹣(﹣2a+6)|=AB=6,
解得a=3或a=﹣1,
∴M(3,6)或(﹣1,2).
25.
解:(1)由题意,从甲医疗机构购买一把体温枪,送一瓶消毒液,则
∴时,只需购买体温枪;时,需要买瓶消毒液;
∵,
∴;
从乙医疗机构购买全部打九折,
∴;
当时,
甲:(元);
乙:(元),
∵,
∴当时,从甲家医疗机构购买费用比较合算.
26.
(1)解:设l1的表达式为y=kx+b(k≠0),
∵l1经过点B(0,2)、点C(3, 3),
∴,解得,
∴l1的函数表达式:y=x+2.
∵点D为l1与x轴的交点,
故令y=0,x+2=0,
解得x=,
∴点D坐标为,0);
(2)解:由(1)同理可得AD所在直线的一次函数表达式为:,
∵点Q在线段上,
∴设点Q坐标为,其中.
∵,
∴,即,
解得,满足题意.
∴点Q坐标为;
(3)解:∵y=kx+k+5=(k+1)x+5,
∴直线l2过定点(-1,5),
∵点A,D到l2的图像的距离相等,
∴当l2与线段AD平行或过线段AD中点,
当l2与线段AD平行时,k=;
当l2过线段AD中点(,2)时,
∴2=k+k+5,
解得:k=;
综上,k的值为或.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
