浙教版八年级数学上册试题 1.5 三角形全等的判定斜边 直角边(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 1.5 三角形全等的判定斜边 直角边(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 494.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览

文档简介
1.5 三角形全等的判定斜边+直角边
一、单选题
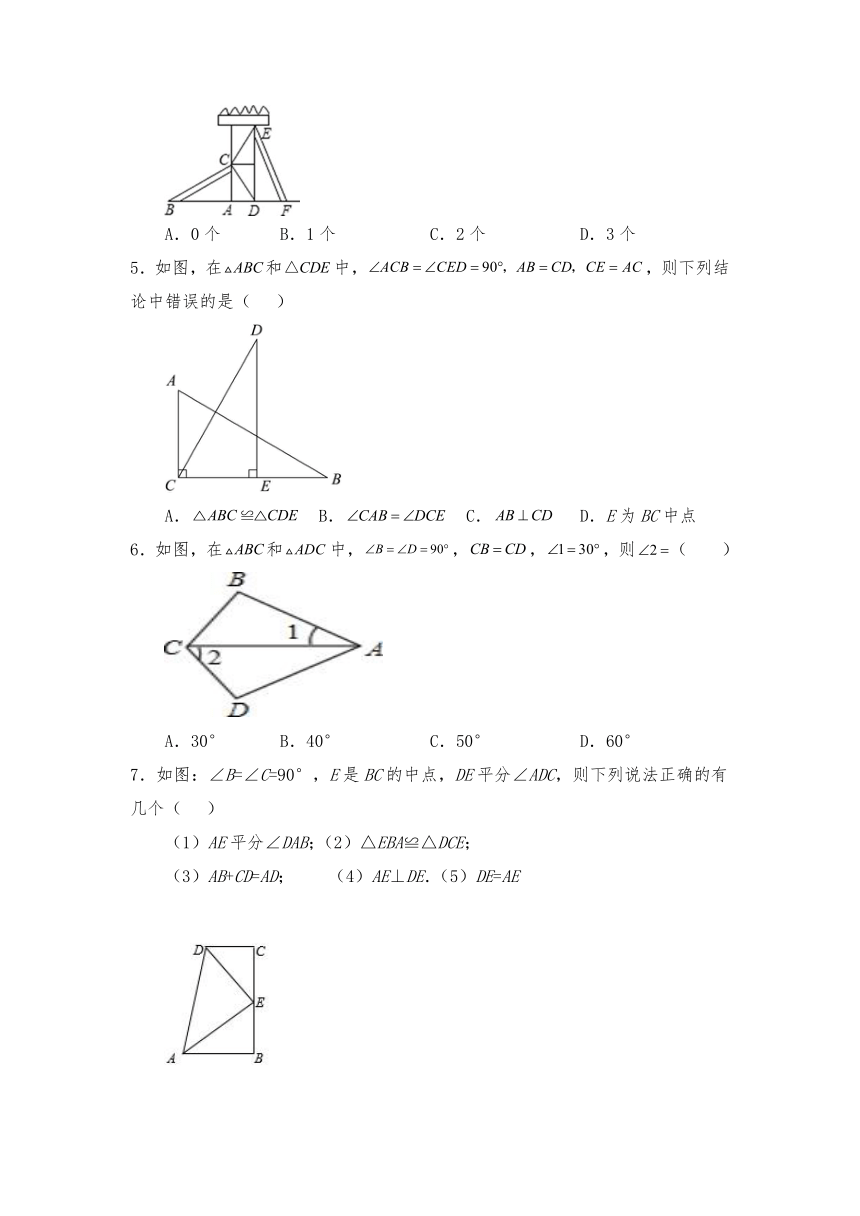
1.如图,若,则的理由是( )
A.SAS B.AAS C.ASA D.HL
2.如图,已知,,若用“”判定和全等,则需要添加的条件是( )
A. B. C. D.
3.如图,,,垂足分别是,,,,则等于( )
A. B. C. D.
4.如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向DF的长度相等,则(1)AB=DE;(2)∠ABC+∠DFE=90°;(3)∠ABC=∠DEF.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
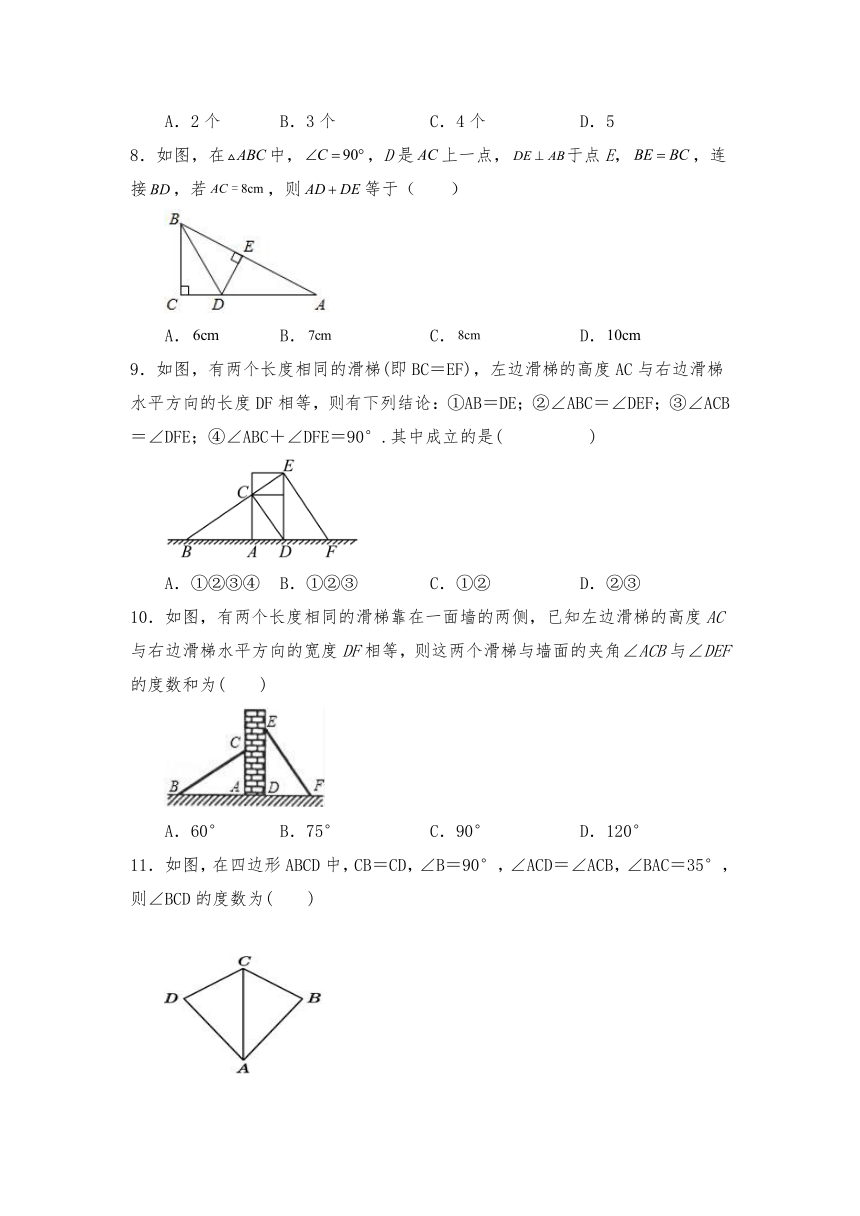
5.如图,在和中,,则下列结论中错误的是( )
A. B. C. D.E为BC中点
6.如图,在和中,,,,则( )
A.30° B.40° C.50° D.60°
7.如图:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,则下列说法正确的有几个( )
(1)AE平分∠DAB;(2)△EBA≌△DCE;
(3)AB+CD=AD; (4)AE⊥DE.(5)DE=AE
A.2个 B.3个 C.4个 D.5
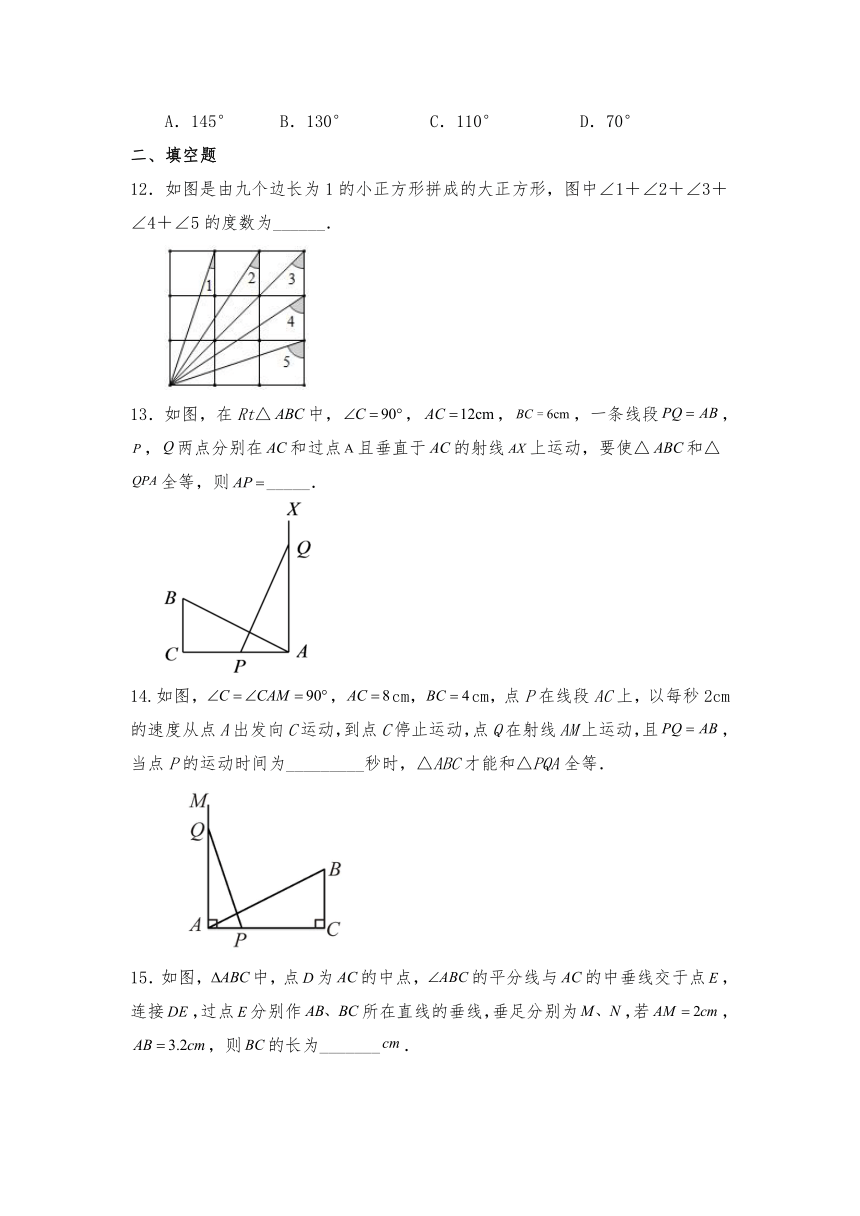
8.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A. B. C. D.
9.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则有下列结论:①AB=DE;②∠ABC=∠DEF;③∠ACB=∠DFE;④∠ABC+∠DFE=90°.其中成立的是( )
A.①②③④ B.①②③ C.①② D.②③
10.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAC=35°,则∠BCD的度数为( )
A.145° B.130° C.110° D.70°
二、填空题
12.如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为______.
13.如图,在Rt△中,,,,一条线段,,两点分别在和过点且垂直于的射线上运动,要使△和△全等,则_____.
14.如图,,cm,cm,点P在线段AC上,以每秒2cm的速度从点A出发向C运动,到点C停止运动,点Q在射线AM上运动,且,当点P的运动时间为_________秒时,△ABC才能和△PQA全等.
15.如图,中,点为的中点,的平分线与的中垂线交于点,连接,过点分别作所在直线的垂线,垂足分别为,若,,则的长为_______.
16.如图,四边形ABCD,连接BD,AB⊥AD,CE⊥BD,AB=CE,BD=CD.若AD=5,CD=7,则BE=________.
17.如图,在四边形中,,,,的延长线与、相邻的两个角的平分线交于点E,若,则的度数为___________.
18.如图,点D、A、E在直线m上,AB=AC,BD⊥m于点D,CE⊥m于点E,且BD=AE.若BD=3,CE=5,则DE=____________
19.如图,在△ABC中,AD⊥BC于点D,过A作AEBC,且AE=AB,AB上有一点F,连接EF.若EF=AC,CD=4BD,则=_____.
20.如图,在△ABC中,AB=AC.点D为△ABC外一点,AE⊥BD于E.∠BDC=∠BAC,DE=3,CD=2,则BE的长为____.
21.如图所示,在ΔABC中, AD平分∠BAC,点E在DA的延长线上,且EF⊥BC,且交BC延长线于点F,H为DC上的一点,且BH=EF, AH=DF, AB=DE,若∠DAC+n∠ACB=90°,则__________.
22.在中,,,,于,,两点分别在边和射线上移动.当,______时,和全等.
23.如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB=____.
三、解答题
24.如图,、相交于点,,于点,于点,且. 求证:.
25.如图,在△ABC中,BC=AB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAB=30°,求∠ACF的度数.
26.已知△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,点D在直线BC上.
(1)如图1,当点D在CB延长线上时,求证:BE⊥CD;
(2)如图2,当D点不在直线BC上时, BE、CD相交于M,
①直接写出∠CME的度数;
②求证:MA平分∠CME
27.动手操作:
如图,已知AB∥CD,点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
问题解决:
(1)若∠ACD=78°,求∠MAB的度数;
(2)若CN⊥AM,垂足为点N,求证:△CAN≌△CMN.
实验探究:
直接写出当∠CAB的度数为多少时 △CAM分别为等边三角形和等腰直角三角形.
答案
单选题
1.D 2.A 3.D 4.D 5.D 6.D
7.B 8.C 9.A 10.C 11.C
二、填空题
12.225°
13.12cm或6cm
14.2或4
15.7.2
16.2
17.
18.8
19.
20.5
21.
22.8或15
23.2
三、解答题
24.
解:∵AE⊥CD,BF⊥CD,
∴∠AEC=∠BFD=90°,
∵和中,
,
∴,
∴∠C=∠D,
∴AC∥BD.
25.
解:(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°,
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL);
∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°。
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=15°+45°=60°
26.(1)解:∵△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,
∴AB=AC,AE=AD,∠DAE+∠DAB=∠CAB+∠DAB,
∴∠CAD=∠BAE,∠C=∠ABC=45°,
∴△CAD≌△BAE(SAS),
∴∠ABE=∠C=45°,
∴∠EBC=∠ABE+∠ABC=90°,即EB⊥CD;
(2)解:①同理可证△BAE≌△CAD,∠ABC=∠ACB=90°,
∴∠ABE=∠ACD,
∵∠EMC=∠EBC+∠BCD,
∴∠EMC=∠ABE+∠ABC+∠ACD+∠BCD=90°;
②如图,过点A作AG⊥BE于G,AF⊥CD于F,
∵△BAE≌△CAD,
∴AG=AF,
在Rt△AGM和Rt△AFM中,
,
∴Rt△AGM≌Rt△AFM(HL),
∴∠AMG=∠AMF,即AM平分∠EMC.
27.
解:(1)∵AB∥CD,
∴∠ACD+∠CAB=180°,
又∵∠ACD=78°,
∴∠CAB=102°.
由作法知,AM是∠CAB的平分线,
∴∠MAB=∠CAB=51°;
(2)证明:由作法知,AM平分∠CAB,
∴∠CAM=∠MAB.
∵AB∥CD,
∴∠MAB=∠CMA,
∴∠CAM=∠CMA,
∵CN⊥AM,
∴∠CNA=∠CNM=90°.
又∵CN=CN,
∴△CAN≌△CMN.
(3)当∠CAB为120°时,△CAM为等边三角形;当∠CAB为90°时,△CAM为等腰直角三角形.
一、单选题
1.如图,若,则的理由是( )
A.SAS B.AAS C.ASA D.HL
2.如图,已知,,若用“”判定和全等,则需要添加的条件是( )
A. B. C. D.
3.如图,,,垂足分别是,,,,则等于( )
A. B. C. D.
4.如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向DF的长度相等,则(1)AB=DE;(2)∠ABC+∠DFE=90°;(3)∠ABC=∠DEF.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.如图,在和中,,则下列结论中错误的是( )
A. B. C. D.E为BC中点
6.如图,在和中,,,,则( )
A.30° B.40° C.50° D.60°
7.如图:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,则下列说法正确的有几个( )
(1)AE平分∠DAB;(2)△EBA≌△DCE;
(3)AB+CD=AD; (4)AE⊥DE.(5)DE=AE
A.2个 B.3个 C.4个 D.5
8.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A. B. C. D.
9.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则有下列结论:①AB=DE;②∠ABC=∠DEF;③∠ACB=∠DFE;④∠ABC+∠DFE=90°.其中成立的是( )
A.①②③④ B.①②③ C.①② D.②③
10.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAC=35°,则∠BCD的度数为( )
A.145° B.130° C.110° D.70°
二、填空题
12.如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为______.
13.如图,在Rt△中,,,,一条线段,,两点分别在和过点且垂直于的射线上运动,要使△和△全等,则_____.
14.如图,,cm,cm,点P在线段AC上,以每秒2cm的速度从点A出发向C运动,到点C停止运动,点Q在射线AM上运动,且,当点P的运动时间为_________秒时,△ABC才能和△PQA全等.
15.如图,中,点为的中点,的平分线与的中垂线交于点,连接,过点分别作所在直线的垂线,垂足分别为,若,,则的长为_______.
16.如图,四边形ABCD,连接BD,AB⊥AD,CE⊥BD,AB=CE,BD=CD.若AD=5,CD=7,则BE=________.
17.如图,在四边形中,,,,的延长线与、相邻的两个角的平分线交于点E,若,则的度数为___________.
18.如图,点D、A、E在直线m上,AB=AC,BD⊥m于点D,CE⊥m于点E,且BD=AE.若BD=3,CE=5,则DE=____________
19.如图,在△ABC中,AD⊥BC于点D,过A作AEBC,且AE=AB,AB上有一点F,连接EF.若EF=AC,CD=4BD,则=_____.
20.如图,在△ABC中,AB=AC.点D为△ABC外一点,AE⊥BD于E.∠BDC=∠BAC,DE=3,CD=2,则BE的长为____.
21.如图所示,在ΔABC中, AD平分∠BAC,点E在DA的延长线上,且EF⊥BC,且交BC延长线于点F,H为DC上的一点,且BH=EF, AH=DF, AB=DE,若∠DAC+n∠ACB=90°,则__________.
22.在中,,,,于,,两点分别在边和射线上移动.当,______时,和全等.
23.如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB=____.
三、解答题
24.如图,、相交于点,,于点,于点,且. 求证:.
25.如图,在△ABC中,BC=AB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAB=30°,求∠ACF的度数.
26.已知△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,点D在直线BC上.
(1)如图1,当点D在CB延长线上时,求证:BE⊥CD;
(2)如图2,当D点不在直线BC上时, BE、CD相交于M,
①直接写出∠CME的度数;
②求证:MA平分∠CME
27.动手操作:
如图,已知AB∥CD,点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
问题解决:
(1)若∠ACD=78°,求∠MAB的度数;
(2)若CN⊥AM,垂足为点N,求证:△CAN≌△CMN.
实验探究:
直接写出当∠CAB的度数为多少时 △CAM分别为等边三角形和等腰直角三角形.
答案
单选题
1.D 2.A 3.D 4.D 5.D 6.D
7.B 8.C 9.A 10.C 11.C
二、填空题
12.225°
13.12cm或6cm
14.2或4
15.7.2
16.2
17.
18.8
19.
20.5
21.
22.8或15
23.2
三、解答题
24.
解:∵AE⊥CD,BF⊥CD,
∴∠AEC=∠BFD=90°,
∵和中,
,
∴,
∴∠C=∠D,
∴AC∥BD.
25.
解:(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°,
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL);
∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°。
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=15°+45°=60°
26.(1)解:∵△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,
∴AB=AC,AE=AD,∠DAE+∠DAB=∠CAB+∠DAB,
∴∠CAD=∠BAE,∠C=∠ABC=45°,
∴△CAD≌△BAE(SAS),
∴∠ABE=∠C=45°,
∴∠EBC=∠ABE+∠ABC=90°,即EB⊥CD;
(2)解:①同理可证△BAE≌△CAD,∠ABC=∠ACB=90°,
∴∠ABE=∠ACD,
∵∠EMC=∠EBC+∠BCD,
∴∠EMC=∠ABE+∠ABC+∠ACD+∠BCD=90°;
②如图,过点A作AG⊥BE于G,AF⊥CD于F,
∵△BAE≌△CAD,
∴AG=AF,
在Rt△AGM和Rt△AFM中,
,
∴Rt△AGM≌Rt△AFM(HL),
∴∠AMG=∠AMF,即AM平分∠EMC.
27.
解:(1)∵AB∥CD,
∴∠ACD+∠CAB=180°,
又∵∠ACD=78°,
∴∠CAB=102°.
由作法知,AM是∠CAB的平分线,
∴∠MAB=∠CAB=51°;
(2)证明:由作法知,AM平分∠CAB,
∴∠CAM=∠MAB.
∵AB∥CD,
∴∠MAB=∠CMA,
∴∠CAM=∠CMA,
∵CN⊥AM,
∴∠CNA=∠CNM=90°.
又∵CN=CN,
∴△CAN≌△CMN.
(3)当∠CAB为120°时,△CAM为等边三角形;当∠CAB为90°时,△CAM为等腰直角三角形.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
