八年级数学上册试题 2.7.2勾股定理与最值问题 -浙教版(含答案)
文档属性
| 名称 | 八年级数学上册试题 2.7.2勾股定理与最值问题 -浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 684.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 12:28:36 | ||
图片预览



文档简介
2.7.2勾股定理与最值问题
一、单选题
1.如图,在长方形纸片ABCD中,AB=3,AD=5,折叠纸片,使点A落在BC边上的A'处,折痕为PQ,当点A'在BC边上移动时,折痕的端点P、Q也随之移动,若限定P、Q分别在AB、AD边上移动,则点A'B最小值和最大值分别为( )
A.1 和 3 B.1 和 4 C.2 和 3 D.2 和 4
2.如图,点,在直线的同侧,到的距离,到的距离,已知,是直线上的一个动点,记的最小值为,的最大值为,则的值为( )
A.160 B.150 C.140 D.130
3.如图,在中,,若是上的一个动点,则的最小值是( )
A.5.5 B.6.4 C.7.4 D.8
4.中,有一点在上移动.若,,的最小值为( )
A.10 B.9.8 C.8.8 D.4.8
5.函数的最小值是( )
A.2 B.3 C.4 D.5
6.如图,在中,,cm,cm,点、分别在、边上.现将沿翻折,使点落在点处.连接,则长度的最小值为( )
A.0 B.2 C.4 D.6
7.如图,在中,,,,为边上一动点,于,于,为中点,则的最小值为( ).
A. B. C. D.
8.已知点是平分线上的一点,且,作于点,点是射线上的一个动点,若,则的最小值为( )
A.2 B.3 C.4 D.5
9.如图,在△ABC中,AB=13,BC=14,S△ABC=84,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A.15 B.12 C.10 D.9
10.如图,在中,,,,点是内的一点,连接,,,满足,则的最小值是( )
A.5 B.6 C.8 D.13
二、填空题
11.如图,是一种饮料的包装盒,长、宽、高分别为4cm,3cm,12cm,现有一长为16cm的吸管插入到盒的底部,则吸管插在盒内部分的长度h的最大值为____________ cm.
12.如图,在三角形ABC中,AB⊥AC于点A,AB=6,AC=8,BC=10,点P是线段BC上的一点,则线段AP的最小值为_____.
13.△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为_____.
14.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值为____________.
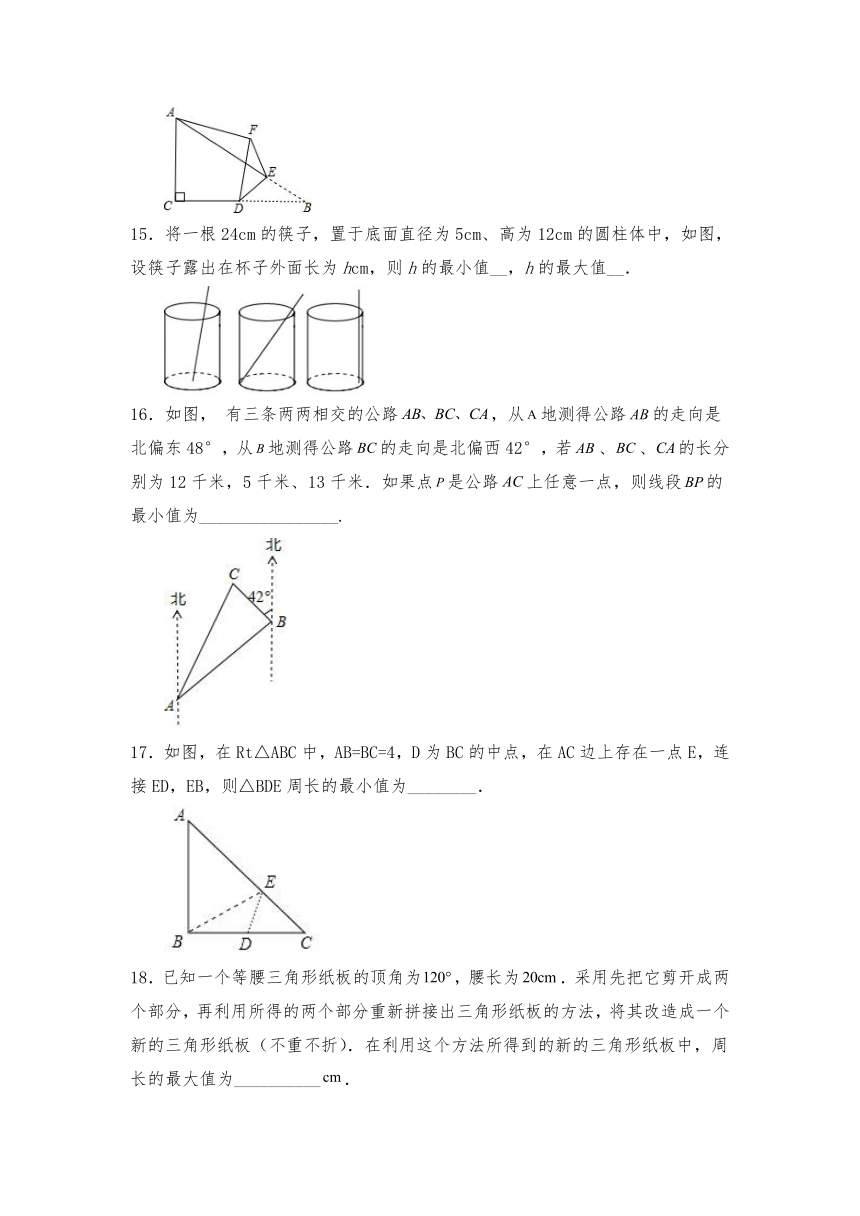
将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值__,h的最大值__.
16.如图, 有三条两两相交的公路,从地测得公路的走向是北偏东48°,从地测得公路的走向是北偏西42°,若、、的长分别为12千米,5千米、13千米.如果点是公路上任意一点,则线段的最小值为________________.
17.如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为________.
18.已知一个等腰三角形纸板的顶角为,腰长为.采用先把它剪开成两个部分,再利用所得的两个部分重新拼接出三角形纸板的方法,将其改造成一个新的三角形纸板(不重不折).在利用这个方法所得到的新的三角形纸板中,周长的最大值为__________.
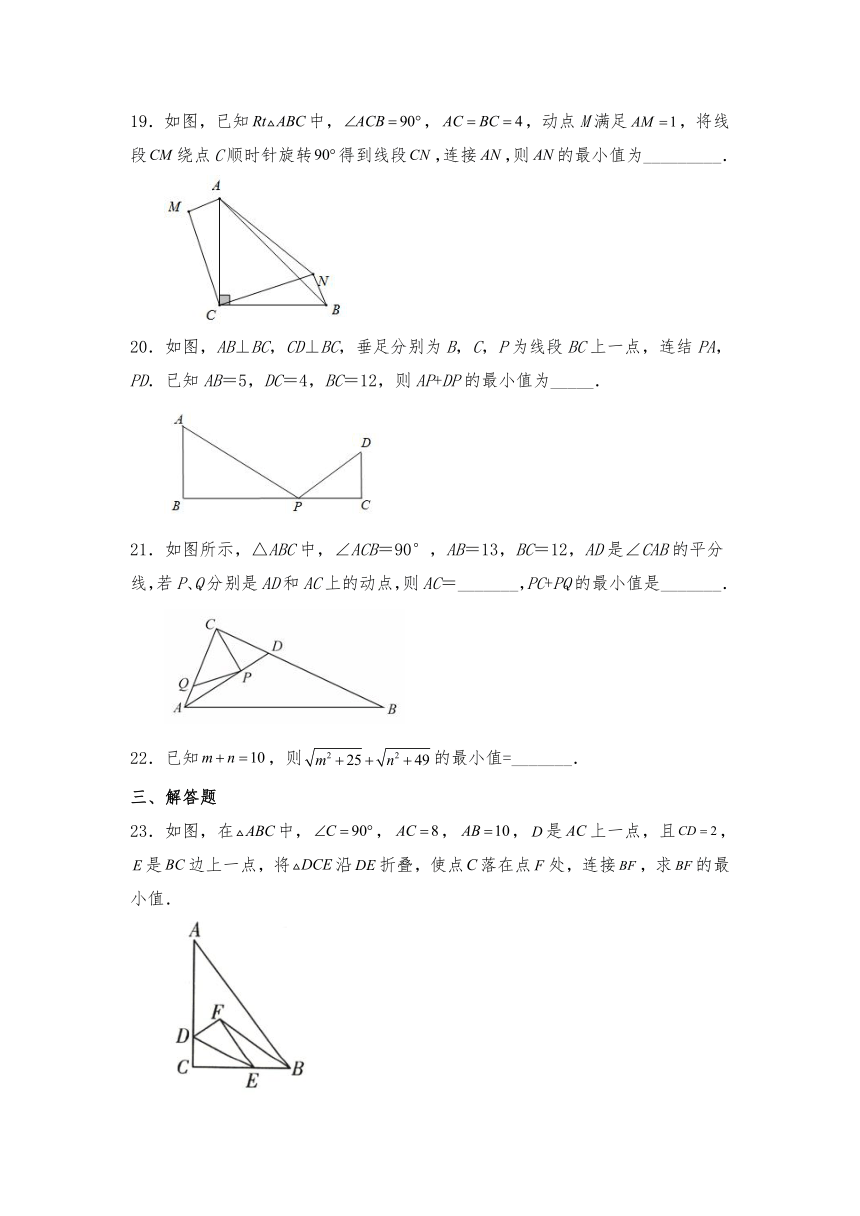
19.如图,已知中,,,动点M满足,将线段绕点C顺时针旋转得到线段,连接,则的最小值为_________.
20.如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连结PA,PD.已知AB=5,DC=4,BC=12,则AP+DP的最小值为_____.
21.如图所示,△ABC中,∠ACB=90°,AB=13,BC=12,AD是∠CAB的平分线,若P、Q分别是AD和AC上的动点,则AC=_______,PC+PQ的最小值是_______.
22.已知,则的最小值=_______.
三、解答题
23.如图,在中,,,,是上一点,且,是边上一点,将沿折叠,使点落在点处,连接,求的最小值.
24.如图,,两个工厂位于一段直线形河道的异侧,工厂至河道的距离为,工厂至河道的距离为,经测量河道上、两地间的距离为,现准备在河边某处(河宽不计)修一个污水处理厂.
(1)设,请用的代数式表示的长______;(结果保留根号)
(2)为了使,两厂到污水处理厂的排污管道之和最短,请在图中画出污水厂位置,并求出排污管道最短长度?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你求出的最小值为多少?
25.如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题:
(1)求线段DE的长度;
(2)若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .
26.在边长为8的等边ABC中,点D是边AB上的一动点,点E在边AC上,且CE = 2AD,射线DE绕点D顺时针旋转60°交BC边于F.
(1)如图1,求证:∠AED = ∠BDF;
(2)如图2,在射线DF上取DP=DE,连接BP,
①求∠DBP的度数;
②取边BC的中点M,当PM取最小值时,求AD的长.
27.(1)问题探究
①如图1,在直角△ABC中,∠BAC=90°,BC=13,AB=5,若P是BC边上一动点,连接AP,求AP的最小值.
②如图2,在等腰直角△ABC中,∠ABC=90°,AC=a,求边AB的长度(用含a的代数式表示).
(2)问题解决
如图3,在等腰直角△ABC中,∠ABC=90°,AC=4,D是边BC的中点,若P是AB边上一动点,E是AC边上一动点,请直接写出PD+PE的最小值.
28.在锐角中,∠BAC=45°.
(1)如图1,BD⊥AC于D,在BD上取点E,使DE=CD,连结AE,F为AC的中点,连结EF并延长至点M,使FM=EF,连结CM、BM.
①求证:△AEF≌△CMF;
②若BC=2,求线段BM 的长.
如图2,P 是△ABC内的一点, (即),AC=3,求PA+PB+PC 的最小值,并求此时∠APC的度数.
答案
一、单选题
1.A 2.A 3.C 4.A 5.D 6.C 7.D 8.B 9.A 10.C
二、填空题
11.13
12.
13.9.8.
14.
15. 11cm 12cm
16.
17.
18.
19.
20.15
21. 5
22.
三、解答题
23.解:如解图,以为圆心,长为半径作圆,
∵,∴点在的一段弧上运
动,连接,交于点,此时最小.
∵,,,,
∴,∴,
∴.
∴的最小值为.
24.(1)解:在Rt△ACE和Rt△BDE中,根据勾股定理可得AE=,BE=,
∴AE+BE=+;
(2)解:根据两点之间线段最短可知,连接AB与CD的交点就是污水处理厂E的位置,如图:
过点B作BF⊥AC于F,则有BF=CD=8,BD=CF=1,
∴AF=AC+CF=6,
在Rt△ABF中,BA===10,
∴排污管道最短长度10km;
(3)解:根据以上推理,可作出下图:
设ED=x,AC=3,DB=2,CD=12.当A、E、B共线时求出AB的值即为原式最小值.
当A、E、B共线时,==13,
即其最小值为13.
故答案为:13.
25.
解:(1)长方形纸片ABCD中,折叠纸片,使点D落在BC边上的点F处,
则AF=AD=BC=10,
BF=,
FC=BC BF=10 6=4,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴DE=EF,
设DE=EF=x,
则EC=DC DE=8 x,
又∵△EFC为直角三角形,
∴FC2+EC2=FE2,
即42+(8 x)2=x2,
∴x=5,
∴DE=5;
(2)连接BP,PF,PD,BD,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴D、F关于AE对称,
∴PF=PD,
则BP+PF=BP+PD≥BD,
∴BP+PF最小为BD,
BD=,
∴BP+PF最小值为:.
故答案为:.
26.
解:(1)在等边△ABC中,∵AB=AC,∠A= ∠ABC=∠C = 60°,
∵∠EDF = 60°,∴∠ADE+∠BDF= ∠ADE+∠AED= 120°,
∴∠AED = ∠BDF;
(2)①方法一:如答题图1,连接EP,过点P作GQ∥BC分别交AB,AC于点G,Q,
易知 △AGQ和△DEP均为等边三角形,
∴BG=CQ,∠AGQ=60°,
∴∠ADE+∠BDF=∠ADE+∠AED=120°,
∴∠AED = ∠BDF,同理∠BDF=∠EPQ,
∴可证:△ADE≌△GPD≌△QEP(AAS),
∴AD=GP=QE,
∵CE = 2AD=CQ+EQ=AD+BG,∴PG=BG,
∴∠DBP=∠BPG=30°;
方法二:如答题图2,在DB上取DG=AE,
∵∠AED = ∠BDF
又∵DP = DE,∴△ADE≌△GPD(SAS),
∴PG = AD,∠PGD=60°,
∵CE =AC-AE =AB-DG =AD+BG=2AD,
∴BG =AD =PG,
∴∠DBP=∠BPG=30°;
②如答图3,在DB上取DG=AE,
由①可知∠MBP=30°, AD =BG =PG;
当时,PM取得最小值;
在Rt△BMP中,∠MBP=30°,BM =4,
∴PM = 2,PB = 2;
过点G作GH⊥BP于点H,∵BG =PG, ∴BH =;
在Rt△BGH中,∠GBP=30°,BH =
∴BG =2,∴AD = BG = 2.
27.(1)①;②AB=a;(2)3
解:(1)问题探究
①如图1,过A作AE⊥CB于E,
在Rt△ABC中,∵∠BAC=90°,AB=5,BC=13,
∴AC==12,
∵=×AB×AC=×BC×AE,
∴AE=
=,
根据垂线段最短可知当AP与AE重合时,AP的值最小,最小值为;
②如图2,
∵∠ABC=90°,AB=AC,
∴,
∵AC=a,
∴,
∴AB=a或AB=﹣a(舍去),
∴AB=a;
(2)问题解决
作关于的对称点 过作于 交AB于,如图3,
则
则最短,
为中点,为等腰直角三角形,
∴AB=BC=2,∠BAC=∠BCA=45°,为等腰直角三角形,
∴BD=CD=,
同理可得:为等腰直角三角形,
PD+PE的最小值为3.
28.解:(1)①∵F为AC的中点,
∴AF=CF
在△AEF和△CMF中
∴△AEF≌△CMF
②由(1)得△AEF≌△CMF,
∴AE=CM,∠DAE=∠FCM,
∵BD⊥AC,∠BAC=45°,
∴AD=BD
在△AED和△BCD中
∴△AED≌△BCD,.
∴AE=BC,∠DAE=∠DBC,
∴BC=CM,∠FCM=∠DBC,
∵∠BCF+∠DBC=90°,
∴∠BCF+∠FCM=90°,
∴△BCM是等腰直角三角形,
由勾股定理得,
(2)将△APB 绕点A逆时针旋转 90°得到△AFE,连接FP、CE,
易知△AFP 是等腰直角三角形,
∴,∠EAC=135°,
作 EH⊥CA 交 CA 的延长线于 H.
在Rt△ EAH 中, ,
∵∠H=90° , ∠EAH=45°,
∵=8,
∴EH=AH=2,
∴CH=5,
在 Rt△EHC 中,
∵PA+PB+PC=FP+EF+PC≥CE,
∴点C、P、F、E四点共线时,PA+PB+PC的最小值为CE,
此时,∠AFP+∠AFE=90°,∠BPC+∠APF=180°,
∵∠AFP=∠APF=45°,
∴∠AFE=∠BPC=135°,
∴∠APB=∠BPC=135°
∴∠APC=360°-135°-135°=90°
∴PA+PB+PC 的最小值为,此时∠APC=90°
一、单选题
1.如图,在长方形纸片ABCD中,AB=3,AD=5,折叠纸片,使点A落在BC边上的A'处,折痕为PQ,当点A'在BC边上移动时,折痕的端点P、Q也随之移动,若限定P、Q分别在AB、AD边上移动,则点A'B最小值和最大值分别为( )
A.1 和 3 B.1 和 4 C.2 和 3 D.2 和 4
2.如图,点,在直线的同侧,到的距离,到的距离,已知,是直线上的一个动点,记的最小值为,的最大值为,则的值为( )
A.160 B.150 C.140 D.130
3.如图,在中,,若是上的一个动点,则的最小值是( )
A.5.5 B.6.4 C.7.4 D.8
4.中,有一点在上移动.若,,的最小值为( )
A.10 B.9.8 C.8.8 D.4.8
5.函数的最小值是( )
A.2 B.3 C.4 D.5
6.如图,在中,,cm,cm,点、分别在、边上.现将沿翻折,使点落在点处.连接,则长度的最小值为( )
A.0 B.2 C.4 D.6
7.如图,在中,,,,为边上一动点,于,于,为中点,则的最小值为( ).
A. B. C. D.
8.已知点是平分线上的一点,且,作于点,点是射线上的一个动点,若,则的最小值为( )
A.2 B.3 C.4 D.5
9.如图,在△ABC中,AB=13,BC=14,S△ABC=84,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A.15 B.12 C.10 D.9
10.如图,在中,,,,点是内的一点,连接,,,满足,则的最小值是( )
A.5 B.6 C.8 D.13
二、填空题
11.如图,是一种饮料的包装盒,长、宽、高分别为4cm,3cm,12cm,现有一长为16cm的吸管插入到盒的底部,则吸管插在盒内部分的长度h的最大值为____________ cm.
12.如图,在三角形ABC中,AB⊥AC于点A,AB=6,AC=8,BC=10,点P是线段BC上的一点,则线段AP的最小值为_____.
13.△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为_____.
14.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值为____________.
将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值__,h的最大值__.
16.如图, 有三条两两相交的公路,从地测得公路的走向是北偏东48°,从地测得公路的走向是北偏西42°,若、、的长分别为12千米,5千米、13千米.如果点是公路上任意一点,则线段的最小值为________________.
17.如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为________.
18.已知一个等腰三角形纸板的顶角为,腰长为.采用先把它剪开成两个部分,再利用所得的两个部分重新拼接出三角形纸板的方法,将其改造成一个新的三角形纸板(不重不折).在利用这个方法所得到的新的三角形纸板中,周长的最大值为__________.
19.如图,已知中,,,动点M满足,将线段绕点C顺时针旋转得到线段,连接,则的最小值为_________.
20.如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连结PA,PD.已知AB=5,DC=4,BC=12,则AP+DP的最小值为_____.
21.如图所示,△ABC中,∠ACB=90°,AB=13,BC=12,AD是∠CAB的平分线,若P、Q分别是AD和AC上的动点,则AC=_______,PC+PQ的最小值是_______.
22.已知,则的最小值=_______.
三、解答题
23.如图,在中,,,,是上一点,且,是边上一点,将沿折叠,使点落在点处,连接,求的最小值.
24.如图,,两个工厂位于一段直线形河道的异侧,工厂至河道的距离为,工厂至河道的距离为,经测量河道上、两地间的距离为,现准备在河边某处(河宽不计)修一个污水处理厂.
(1)设,请用的代数式表示的长______;(结果保留根号)
(2)为了使,两厂到污水处理厂的排污管道之和最短,请在图中画出污水厂位置,并求出排污管道最短长度?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你求出的最小值为多少?
25.如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题:
(1)求线段DE的长度;
(2)若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .
26.在边长为8的等边ABC中,点D是边AB上的一动点,点E在边AC上,且CE = 2AD,射线DE绕点D顺时针旋转60°交BC边于F.
(1)如图1,求证:∠AED = ∠BDF;
(2)如图2,在射线DF上取DP=DE,连接BP,
①求∠DBP的度数;
②取边BC的中点M,当PM取最小值时,求AD的长.
27.(1)问题探究
①如图1,在直角△ABC中,∠BAC=90°,BC=13,AB=5,若P是BC边上一动点,连接AP,求AP的最小值.
②如图2,在等腰直角△ABC中,∠ABC=90°,AC=a,求边AB的长度(用含a的代数式表示).
(2)问题解决
如图3,在等腰直角△ABC中,∠ABC=90°,AC=4,D是边BC的中点,若P是AB边上一动点,E是AC边上一动点,请直接写出PD+PE的最小值.
28.在锐角中,∠BAC=45°.
(1)如图1,BD⊥AC于D,在BD上取点E,使DE=CD,连结AE,F为AC的中点,连结EF并延长至点M,使FM=EF,连结CM、BM.
①求证:△AEF≌△CMF;
②若BC=2,求线段BM 的长.
如图2,P 是△ABC内的一点, (即),AC=3,求PA+PB+PC 的最小值,并求此时∠APC的度数.
答案
一、单选题
1.A 2.A 3.C 4.A 5.D 6.C 7.D 8.B 9.A 10.C
二、填空题
11.13
12.
13.9.8.
14.
15. 11cm 12cm
16.
17.
18.
19.
20.15
21. 5
22.
三、解答题
23.解:如解图,以为圆心,长为半径作圆,
∵,∴点在的一段弧上运
动,连接,交于点,此时最小.
∵,,,,
∴,∴,
∴.
∴的最小值为.
24.(1)解:在Rt△ACE和Rt△BDE中,根据勾股定理可得AE=,BE=,
∴AE+BE=+;
(2)解:根据两点之间线段最短可知,连接AB与CD的交点就是污水处理厂E的位置,如图:
过点B作BF⊥AC于F,则有BF=CD=8,BD=CF=1,
∴AF=AC+CF=6,
在Rt△ABF中,BA===10,
∴排污管道最短长度10km;
(3)解:根据以上推理,可作出下图:
设ED=x,AC=3,DB=2,CD=12.当A、E、B共线时求出AB的值即为原式最小值.
当A、E、B共线时,==13,
即其最小值为13.
故答案为:13.
25.
解:(1)长方形纸片ABCD中,折叠纸片,使点D落在BC边上的点F处,
则AF=AD=BC=10,
BF=,
FC=BC BF=10 6=4,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴DE=EF,
设DE=EF=x,
则EC=DC DE=8 x,
又∵△EFC为直角三角形,
∴FC2+EC2=FE2,
即42+(8 x)2=x2,
∴x=5,
∴DE=5;
(2)连接BP,PF,PD,BD,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴D、F关于AE对称,
∴PF=PD,
则BP+PF=BP+PD≥BD,
∴BP+PF最小为BD,
BD=,
∴BP+PF最小值为:.
故答案为:.
26.
解:(1)在等边△ABC中,∵AB=AC,∠A= ∠ABC=∠C = 60°,
∵∠EDF = 60°,∴∠ADE+∠BDF= ∠ADE+∠AED= 120°,
∴∠AED = ∠BDF;
(2)①方法一:如答题图1,连接EP,过点P作GQ∥BC分别交AB,AC于点G,Q,
易知 △AGQ和△DEP均为等边三角形,
∴BG=CQ,∠AGQ=60°,
∴∠ADE+∠BDF=∠ADE+∠AED=120°,
∴∠AED = ∠BDF,同理∠BDF=∠EPQ,
∴可证:△ADE≌△GPD≌△QEP(AAS),
∴AD=GP=QE,
∵CE = 2AD=CQ+EQ=AD+BG,∴PG=BG,
∴∠DBP=∠BPG=30°;
方法二:如答题图2,在DB上取DG=AE,
∵∠AED = ∠BDF
又∵DP = DE,∴△ADE≌△GPD(SAS),
∴PG = AD,∠PGD=60°,
∵CE =AC-AE =AB-DG =AD+BG=2AD,
∴BG =AD =PG,
∴∠DBP=∠BPG=30°;
②如答图3,在DB上取DG=AE,
由①可知∠MBP=30°, AD =BG =PG;
当时,PM取得最小值;
在Rt△BMP中,∠MBP=30°,BM =4,
∴PM = 2,PB = 2;
过点G作GH⊥BP于点H,∵BG =PG, ∴BH =;
在Rt△BGH中,∠GBP=30°,BH =
∴BG =2,∴AD = BG = 2.
27.(1)①;②AB=a;(2)3
解:(1)问题探究
①如图1,过A作AE⊥CB于E,
在Rt△ABC中,∵∠BAC=90°,AB=5,BC=13,
∴AC==12,
∵=×AB×AC=×BC×AE,
∴AE=
=,
根据垂线段最短可知当AP与AE重合时,AP的值最小,最小值为;
②如图2,
∵∠ABC=90°,AB=AC,
∴,
∵AC=a,
∴,
∴AB=a或AB=﹣a(舍去),
∴AB=a;
(2)问题解决
作关于的对称点 过作于 交AB于,如图3,
则
则最短,
为中点,为等腰直角三角形,
∴AB=BC=2,∠BAC=∠BCA=45°,为等腰直角三角形,
∴BD=CD=,
同理可得:为等腰直角三角形,
PD+PE的最小值为3.
28.解:(1)①∵F为AC的中点,
∴AF=CF
在△AEF和△CMF中
∴△AEF≌△CMF
②由(1)得△AEF≌△CMF,
∴AE=CM,∠DAE=∠FCM,
∵BD⊥AC,∠BAC=45°,
∴AD=BD
在△AED和△BCD中
∴△AED≌△BCD,.
∴AE=BC,∠DAE=∠DBC,
∴BC=CM,∠FCM=∠DBC,
∵∠BCF+∠DBC=90°,
∴∠BCF+∠FCM=90°,
∴△BCM是等腰直角三角形,
由勾股定理得,
(2)将△APB 绕点A逆时针旋转 90°得到△AFE,连接FP、CE,
易知△AFP 是等腰直角三角形,
∴,∠EAC=135°,
作 EH⊥CA 交 CA 的延长线于 H.
在Rt△ EAH 中, ,
∵∠H=90° , ∠EAH=45°,
∵=8,
∴EH=AH=2,
∴CH=5,
在 Rt△EHC 中,
∵PA+PB+PC=FP+EF+PC≥CE,
∴点C、P、F、E四点共线时,PA+PB+PC的最小值为CE,
此时,∠AFP+∠AFE=90°,∠BPC+∠APF=180°,
∵∠AFP=∠APF=45°,
∴∠AFE=∠BPC=135°,
∴∠APB=∠BPC=135°
∴∠APC=360°-135°-135°=90°
∴PA+PB+PC 的最小值为,此时∠APC=90°
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
