八年级数学上册试题 5.2 函数同步练习-浙教版(含答案)
文档属性
| 名称 | 八年级数学上册试题 5.2 函数同步练习-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 369.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览




文档简介
5.2 函数
一、单选题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器的容积
2.下列各曲线中不能表示y是x的函数的是( )
A.B.C. D.
3.等腰三角形的周长是60cm,腰长(cm)与底边长(cm)的函数解析式正确的是( )
A. B.
C. D.
4.函数y=中,自变量x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
5.下面哪个点不在函数的图像上( )
A.(3,0) B.(0.5,2) C.(-5,13) D.(1,1)
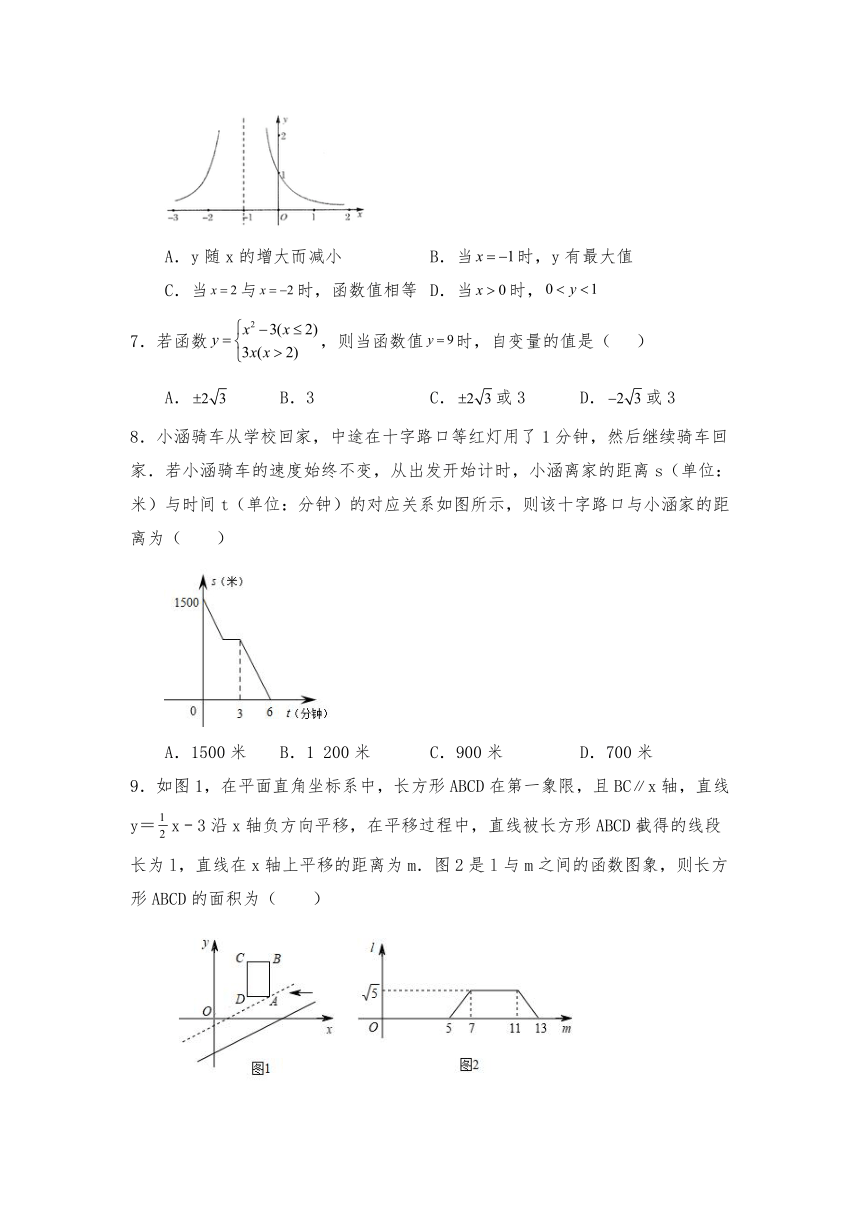
6.结合学习函数的经验,小红在平面直角坐标系中画出了函数的图象,如图所示.根据图象,小红得到了该函数四条结论,其中正确的是( )
A.y随x的增大而减小 B.当时,y有最大值
C.当与时,函数值相等 D.当时,
7.若函数,则当函数值时,自变量的值是( )
A. B.3 C.或3 D.或3
8.小涵骑车从学校回家,中途在十字路口等红灯用了1分钟,然后继续骑车回家.若小涵骑车的速度始终不变,从出发开始计时,小涵离家的距离s(单位:米)与时间t(单位:分钟)的对应关系如图所示,则该十字路口与小涵家的距离为( )
A.1500米 B.1 200米 C.900米 D.700米
9.如图1,在平面直角坐标系中,长方形ABCD在第一象限,且BCx轴,直线y=x﹣3沿x轴负方向平移,在平移过程中,直线被长方形ABCD截得的线段长为l,直线在x轴上平移的距离为m.图2是l与m之间的函数图象,则长方形ABCD的面积为( )
A.2 B.6 C.8 D.12
10.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,把线段AB以A为旋转中心,逆时针方向旋转90°,得到线段AC,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.B.C. D.
二、填空题
11.在函数y=中,自变量x的取值范围是_____.
12.下列各项:①;②;③;④;具有函数关系(自变量为)的是_____________.(填序号)
13.若对于所有的实数,都有,则______.
14.根据表格中的数据规律,当x=-4时,y的值是________.
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的.设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分钟)之间的函数关系如图所示.根据图象信息给出下列说法:①每分钟进水5升;②当4≤x≤12时,容器中的水量在减少;③若12分钟后只放水,不进水,还要8分钟可以把水放完;④若从一开始进出水管同时打开,则需要24分钟可以将容器灌满.其中正确的有________(填序号).
16.汽车开始行驶时,油箱中有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为_____,该汽车最多可行驶_____小时.
17.甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发__秒.
18.如图,,点从出发,沿路线运动,到停止;点的速度为每秒,运动时间为秒,如图是的面积与秒的图象.根据题目中提供的信息,请你推断出______.
三、解答题
19.已知,求的值.
20.一辆小汽车在公路上从静止到启动5s内的速度随时间的变化情况如下表:
时间t/s 0 1 2 3 4 5
速度v/m/s 0 0.3 1.3 2.8 2.6 4.5
(1)上表反映了哪两个变量之间的关系?
(2)随着时间(s)的变化,速度v(m/s)的变化趋势是什么?
(3)当t每增加1s,v的变化情况相同吗?在哪个时间段(相邻两秒之间,如1s~2s)内,v增加的最快?
21.链条是自行车传动系统上的重要组成部分,如图所示,如果每节链条的长度为a,交叉重叠部分的圆的直径为b.
(1)当链条由5节组成时,链条的总长度是_______.(用含a、b的代数式表示)
(2)当链条由x节组成时,链条的总长度是y,求y与x之间的函数关系式.
(3)如果一辆某型号自行车的链条是由若干节这样的链条组成,每节链条的长度为2cm,交叉重叠部分的圆的直径为0.8cm.这辆自行车上的链条(安装后)的总长度为144.8cm.求需要多少节这样的链条.
22.一慢车和一快车沿相同路线从A地到B地,两车所行的路程s(千米)与慢车行驶的时间x(时)关系如图所示.根据图像解决下列问题:
(1)快车比慢车晚 小时出发,快车比慢车早到 小时.快车追上慢车时,快车行驶了 千米.
(2)求A、B两地相距多少千米?
23.如图1,在Rt△ABC中,AC=BC,点D在AC边上,以CD为边在AC的右侧作正方形CDEF.点P以每秒1cm的速度沿F→E→D→A→B的路径运动,连接BP、CP,△BCP的面积y()与运动时间x(秒)之间的图象关系如图2所示.
(1) 求EF的长度和a的值;
(2) 当x=6时,连接AF,判断BP与AF的数量关系,说明理由.
24.小慧根据学习函数的经验,对函数y=|x-1|的图像与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
(4)函数y=|x-1|的最小值为 .
答案
一、单选题
1.B 2.B 3.A 4.B 5.A 6.D 7.D 8.C 9.B 10.A
二、填空题
11.1≤x≤2
12.①②④
13.0
14.-64
15.①③④
16. y=40﹣5x 8
17.15
18.
三、解答题
19.
解:依题意得:,,
∴,
则.
20.
解:(1)上表反映了时间与速度之间的关系;
(2)v的变化趋势是t从0~3s和4~5s,v随着t的增大而增大,
而t从3~4s,v随着t的增大而减小.
(3)在0~1s时,v增加0.3m/s;
在1~2s时,,v增加1m/s;
在2~3s时,,v增加1.5m/s;
在3~4s时,,v减小0.2m/s;
在4~5s时,,v增加1.9m/s;
所以当t每增加1s,v的变化情况不相同,在第4~5s时,v增加得最快.
21.(1)解:根据图形可得出:5节链条的长度为:5a-4b.
故答案为:5a-4b;
(2)解:由图形可得,x节链条长为:y=ax-b(x-1)=ax-bx+b;
∴y与x之间的关系式为:y=ax-bx+b;
(3)解:根据题意可知,当a=2,b=0.8时,y=144.8.
即2x-0.8x+0.8=144.8,
解得x=120.
答:需要120节这样的链条.
22.
(1)解:由图像可得,
慢车比快车晚2小时出发,快车比慢车早到18﹣14=4(小时),快车追上慢车时,快行驶了276千米,
故答案为:2,4,276;
(2)解:由图像可得,
慢车的速度为:276÷6=46(千米/时),
46×18=828(千米),
答:A、B两地相距828千米.
23.(1)解:当点P在边EF上运动时,
y=S△BCPBC PFBC×1×xBC x,
∵BC为定值,
∴y随x的增大而增大,
∴当x=3时,y=a,
此时EF=1×3=3(cm),
当点P在边ED上运动时,点P到BC的距离等于3,
y=S△BCPBC×3BC,
∴y的值不变,
∵四边形FEDC是正方形,
∴DE=EF=3cm,
∴x6(秒),
∴b=6,
当点P在DA上运动时,
y=S△PBCBC PC,
∴y随PC的增大而增大,
当点P与点A重合时,即x=8时,y最大,
此时AD=8×1﹣3﹣3=2,
∴AC=BC=3+2=5(cm),
∴aBC×EF5×3;
(2)由(1)知,当点x=6时,点P在点D处,如图所示:
此时,BD=AF,理由:
∵BC=AC,CD=CF,∠ACB=∠ACF=90°,
∴△BDC≌△AFC(SAS),
∴BD=AF.
24.
解:(1)函数y=|x-1|的自变量x的取值范围是全体实数,
故答案为:全体实数.
(2)当x=-1时,y=|x-1|=2,
故b=2,
故答案为:2.
(3)根据列表,画图像如下:
.
(4)∵|x-1|≥0,
∴y的最小值为0,
故答案为:0.
一、单选题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器的容积
2.下列各曲线中不能表示y是x的函数的是( )
A.B.C. D.
3.等腰三角形的周长是60cm,腰长(cm)与底边长(cm)的函数解析式正确的是( )
A. B.
C. D.
4.函数y=中,自变量x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
5.下面哪个点不在函数的图像上( )
A.(3,0) B.(0.5,2) C.(-5,13) D.(1,1)
6.结合学习函数的经验,小红在平面直角坐标系中画出了函数的图象,如图所示.根据图象,小红得到了该函数四条结论,其中正确的是( )
A.y随x的增大而减小 B.当时,y有最大值
C.当与时,函数值相等 D.当时,
7.若函数,则当函数值时,自变量的值是( )
A. B.3 C.或3 D.或3
8.小涵骑车从学校回家,中途在十字路口等红灯用了1分钟,然后继续骑车回家.若小涵骑车的速度始终不变,从出发开始计时,小涵离家的距离s(单位:米)与时间t(单位:分钟)的对应关系如图所示,则该十字路口与小涵家的距离为( )
A.1500米 B.1 200米 C.900米 D.700米
9.如图1,在平面直角坐标系中,长方形ABCD在第一象限,且BCx轴,直线y=x﹣3沿x轴负方向平移,在平移过程中,直线被长方形ABCD截得的线段长为l,直线在x轴上平移的距离为m.图2是l与m之间的函数图象,则长方形ABCD的面积为( )
A.2 B.6 C.8 D.12
10.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,把线段AB以A为旋转中心,逆时针方向旋转90°,得到线段AC,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.B.C. D.
二、填空题
11.在函数y=中,自变量x的取值范围是_____.
12.下列各项:①;②;③;④;具有函数关系(自变量为)的是_____________.(填序号)
13.若对于所有的实数,都有,则______.
14.根据表格中的数据规律,当x=-4时,y的值是________.
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的.设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分钟)之间的函数关系如图所示.根据图象信息给出下列说法:①每分钟进水5升;②当4≤x≤12时,容器中的水量在减少;③若12分钟后只放水,不进水,还要8分钟可以把水放完;④若从一开始进出水管同时打开,则需要24分钟可以将容器灌满.其中正确的有________(填序号).
16.汽车开始行驶时,油箱中有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为_____,该汽车最多可行驶_____小时.
17.甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发__秒.
18.如图,,点从出发,沿路线运动,到停止;点的速度为每秒,运动时间为秒,如图是的面积与秒的图象.根据题目中提供的信息,请你推断出______.
三、解答题
19.已知,求的值.
20.一辆小汽车在公路上从静止到启动5s内的速度随时间的变化情况如下表:
时间t/s 0 1 2 3 4 5
速度v/m/s 0 0.3 1.3 2.8 2.6 4.5
(1)上表反映了哪两个变量之间的关系?
(2)随着时间(s)的变化,速度v(m/s)的变化趋势是什么?
(3)当t每增加1s,v的变化情况相同吗?在哪个时间段(相邻两秒之间,如1s~2s)内,v增加的最快?
21.链条是自行车传动系统上的重要组成部分,如图所示,如果每节链条的长度为a,交叉重叠部分的圆的直径为b.
(1)当链条由5节组成时,链条的总长度是_______.(用含a、b的代数式表示)
(2)当链条由x节组成时,链条的总长度是y,求y与x之间的函数关系式.
(3)如果一辆某型号自行车的链条是由若干节这样的链条组成,每节链条的长度为2cm,交叉重叠部分的圆的直径为0.8cm.这辆自行车上的链条(安装后)的总长度为144.8cm.求需要多少节这样的链条.
22.一慢车和一快车沿相同路线从A地到B地,两车所行的路程s(千米)与慢车行驶的时间x(时)关系如图所示.根据图像解决下列问题:
(1)快车比慢车晚 小时出发,快车比慢车早到 小时.快车追上慢车时,快车行驶了 千米.
(2)求A、B两地相距多少千米?
23.如图1,在Rt△ABC中,AC=BC,点D在AC边上,以CD为边在AC的右侧作正方形CDEF.点P以每秒1cm的速度沿F→E→D→A→B的路径运动,连接BP、CP,△BCP的面积y()与运动时间x(秒)之间的图象关系如图2所示.
(1) 求EF的长度和a的值;
(2) 当x=6时,连接AF,判断BP与AF的数量关系,说明理由.
24.小慧根据学习函数的经验,对函数y=|x-1|的图像与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
(4)函数y=|x-1|的最小值为 .
答案
一、单选题
1.B 2.B 3.A 4.B 5.A 6.D 7.D 8.C 9.B 10.A
二、填空题
11.1≤x≤2
12.①②④
13.0
14.-64
15.①③④
16. y=40﹣5x 8
17.15
18.
三、解答题
19.
解:依题意得:,,
∴,
则.
20.
解:(1)上表反映了时间与速度之间的关系;
(2)v的变化趋势是t从0~3s和4~5s,v随着t的增大而增大,
而t从3~4s,v随着t的增大而减小.
(3)在0~1s时,v增加0.3m/s;
在1~2s时,,v增加1m/s;
在2~3s时,,v增加1.5m/s;
在3~4s时,,v减小0.2m/s;
在4~5s时,,v增加1.9m/s;
所以当t每增加1s,v的变化情况不相同,在第4~5s时,v增加得最快.
21.(1)解:根据图形可得出:5节链条的长度为:5a-4b.
故答案为:5a-4b;
(2)解:由图形可得,x节链条长为:y=ax-b(x-1)=ax-bx+b;
∴y与x之间的关系式为:y=ax-bx+b;
(3)解:根据题意可知,当a=2,b=0.8时,y=144.8.
即2x-0.8x+0.8=144.8,
解得x=120.
答:需要120节这样的链条.
22.
(1)解:由图像可得,
慢车比快车晚2小时出发,快车比慢车早到18﹣14=4(小时),快车追上慢车时,快行驶了276千米,
故答案为:2,4,276;
(2)解:由图像可得,
慢车的速度为:276÷6=46(千米/时),
46×18=828(千米),
答:A、B两地相距828千米.
23.(1)解:当点P在边EF上运动时,
y=S△BCPBC PFBC×1×xBC x,
∵BC为定值,
∴y随x的增大而增大,
∴当x=3时,y=a,
此时EF=1×3=3(cm),
当点P在边ED上运动时,点P到BC的距离等于3,
y=S△BCPBC×3BC,
∴y的值不变,
∵四边形FEDC是正方形,
∴DE=EF=3cm,
∴x6(秒),
∴b=6,
当点P在DA上运动时,
y=S△PBCBC PC,
∴y随PC的增大而增大,
当点P与点A重合时,即x=8时,y最大,
此时AD=8×1﹣3﹣3=2,
∴AC=BC=3+2=5(cm),
∴aBC×EF5×3;
(2)由(1)知,当点x=6时,点P在点D处,如图所示:
此时,BD=AF,理由:
∵BC=AC,CD=CF,∠ACB=∠ACF=90°,
∴△BDC≌△AFC(SAS),
∴BD=AF.
24.
解:(1)函数y=|x-1|的自变量x的取值范围是全体实数,
故答案为:全体实数.
(2)当x=-1时,y=|x-1|=2,
故b=2,
故答案为:2.
(3)根据列表,画图像如下:
.
(4)∵|x-1|≥0,
∴y的最小值为0,
故答案为:0.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
