八年级数学上册试题 5.2函数同步测试-浙教版(含答案)
文档属性
| 名称 | 八年级数学上册试题 5.2函数同步测试-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 教案 | ||
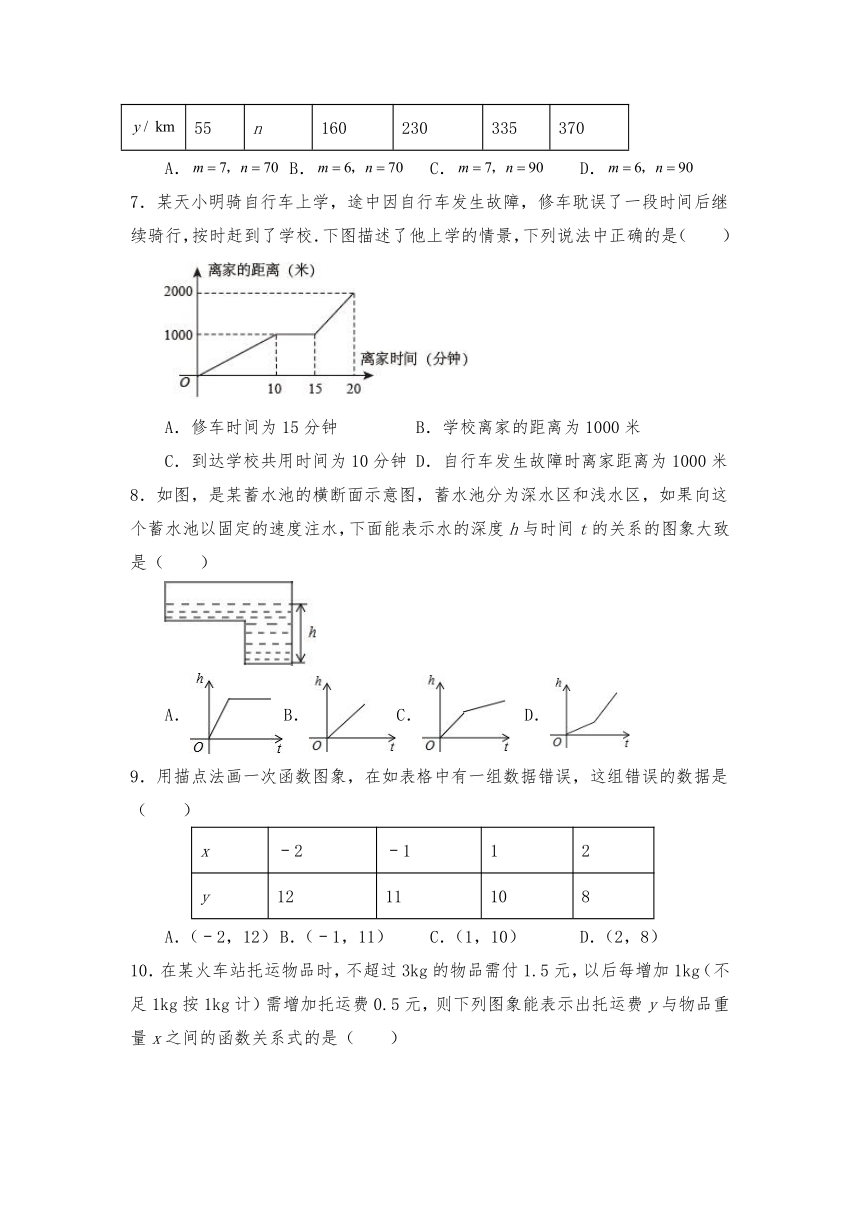
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 12:37:30 | ||
图片预览



文档简介
5.2函数
一、单选题
1.下列表示y与x之间关系的图象中,y不是x的函数关系的是( )
A.B.C.D.
2.2022年春节期间,疫情形势复杂,张红遵循“防疫当前,本地过年”的原则,给远在家乡的家人打电话拜年.电话费随着时间的变化而变化,在这个过程中,因变量是( )
A.张红 B.电话费 C.时间 D.家人
3.在函数中,当自变量时,函数值等于( )
A.1 B.4 C.7 D.13
4.下面哪个点不在函数的图像上( )
A.(3,0) B.(0.5,2) C.(-5,13) D.(1,1)
5.如图,y=2x+10表示了自变量x与因变量y的关系,当x每增加1时,y增加( )
A.1 B.2 C.6 D.12
6.地表以下岩层的温度y()随着所处深度x()的变化而变化,在某个地点y与x之间的关系可以近似地用关系式来表示,也可用表格表示,其中表格的部分数据如下表所示,则其中的m,n分别是( )
1 2 4 m 9 10
55 n 160 230 335 370
A. B. C. D.
7.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.下图描述了他上学的情景,下列说法中正确的是( )
A.修车时间为15分钟 B.学校离家的距离为1000米
C.到达学校共用时间为10分钟 D.自行车发生故障时离家距离为1000米
8.如图,是某蓄水池的横断面示意图,蓄水池分为深水区和浅水区,如果向这个蓄水池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是( )
A.B.C. D.
9.用描点法画一次函数图象,在如表格中有一组数据错误,这组错误的数据是( )
x ﹣2 ﹣1 1 2
y 12 11 10 8
A.(﹣2,12) B.(﹣1,11) C.(1,10) D.(2,8)
10.在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是( )
A. B.
C. D.
二、填空题
11.函数的定义域为________.
12.变量,有如下关系:①;②.其中是的函数的是________.(填序号)
13.变量y与x之间的关系式为,当自变量时,因变量y的值为________.
14.小军用100元去买单价为5元的笔记本,他买完笔记本之后剩余的钱y元与买这种笔记本数量x本(,x为正整数)之间的关系式为______.
15.某文具店“六一”期间开展促销活动,销售总价与卖出笔记本数量的关系如表:
数量(件) 1 2 3 4 5 …
销售总价(元) 8 14 20 26 32 …
则售价与数量之间的关系式是______.
16.如表是加热食用油时温度随时间的变化情况:
时间 0 10 20 30 40
油温 10 30 50 70 90
王红发现,烧到时油沸腾了,则油的沸点是__________(沸点是指液体沸腾时候的温度).
17.根据如图所示的程序计算:若输入自变量x的值为,则输出的结果是_________________.
18.如图1,在长方形ABCD中,动点P从点B出发,沿方向匀速运动至点A停止,已知点P的运动速度为,设点P的运动时间为,的面积为,若关于的图像如图2所示,则长方形ABCD的面积为______.
三、解答题
19.已知一个长方形的长为x,宽为y,周长为40.
(1) 求出y关于x的函数解析式(不用写出自变量x的取值范围);
(2) 当时,求y的值;
(3) 当时,该长方形的面积是多少
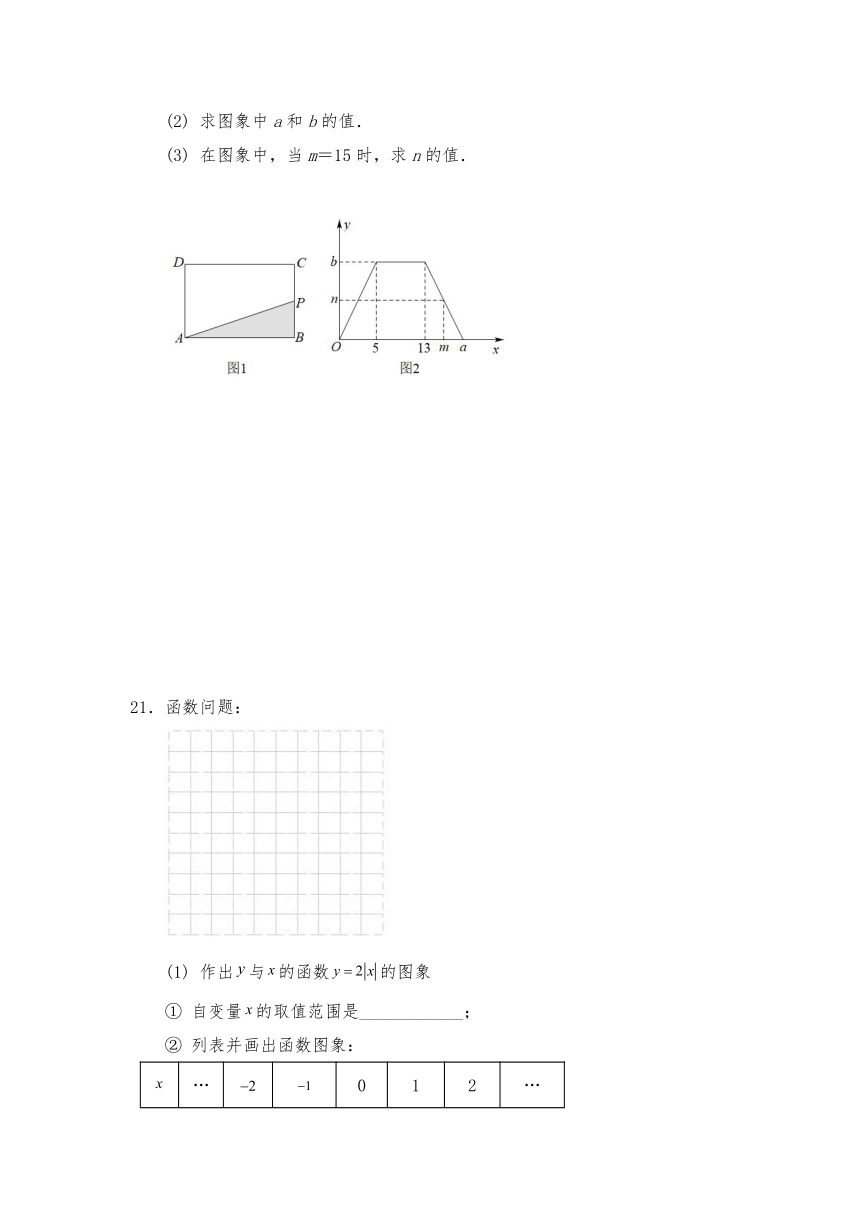
20.如图1,在长方形ABCD中,点P从点B出发,沿B→C→D→A运动到点A停止.设点P的运动路程为x,△PAB的面积为y,y与x的关系图象如图2所示.
(1) AB的长度为______,BC的长度为______.
(2) 求图象中a和b的值.
(3) 在图象中,当m=15时,求n的值.
21.函数问题:
作出与的函数的图象
① 自变量的取值范围是____________;
② 列表并画出函数图象:
… 0 1 2 …
… …
③ 当自变量的值从1增加到2时,则函数的值增加了____________.
(2) 在一个变化的过程中,两个变量与之间可能是函数关系,也可能不是函数关系:
下列各式中, 是的函数的是____________.
①; ②; ③; ④;
22.某公交车每天的支出费用为600元,每天乘车人数
(人)与每天利润(利润=票款收入-支出费用)(元)的变化关系,如下表所示(每位乘客的乘车票价固定不变):
(人) … 200 250 300 350 400 …
(元) … -200 -100 0 100 200 …
根据表格中的数据,回答下列问题:
观察表中数据可知,当乘客量达到______人以上时,该公交车才不会亏损;票价为______(元/人);
请写出公交车每天利润(元)与每天乘车人数(人)的关系式:______;
当一天乘客人数为多少人时,利润是1000元?
23.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示)与x之间的函数关系.根据图象进行以下探究:
[信息读取]
(1)甲,乙两地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需______小时,普通列车的速度是______千米/小时:
[解决问题]
(3)求动车的速度:
(4)求点C的坐标.
24.小泽根据学习函数的经验,对函数的图象与性质进行了探究.下面是小泽的探究过程,请补充完成:
函数的自变量的取值范围是 ,函数值的取值范围是 ;
(2) 下表为与的几组对应值:
1 2 3 4 5
0 1 1.41 1.73 2
在所给的平面直角坐标系中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(3) 当时,对应的函数值约为 ;
(4) 结合图象写出该函数的一条性质: .
答案
一、单选题
1.C 2.B 3.C 4.A 5.B 6.D 7.D 8.C 9.C 10.D
二、填空题
11.x1
12.①
13.17
14.
15.y=2+6x
16.224
17.0.5
18.
三、解答题
19.
解:(1)∵长方形的周长为40,
∴2(x+y)=40,
∴y=-x+20;
(2)当x=13时,
y=20-13
=7;
(3)当y=8时,20-x=8,
∴x=12,
∴长方形的面积=12×8=96.
20.(1)解:由图2知,当x=5时,点P与C重合,
∴BC=5,
当x=13时,点P与D重合,
∴BC+CD=13,
∴CD=8=AB,
故答案为:8,5;
(2)当P与C点重合时,
=,
当点P与A重合时,
=5+8+5=18;
(3)∵,
∴此时点P在AD边上,且AP=3.
∴.
21.(1)解:①在函数中,x的取值范实为全体实数,
故答案为:全体实数;
②列表如下:
-2 -1 0 1 2
4 2 0 2 4
函数变形为或,画图如下:
③当时,,当时,,
所以当自变量的值从1增加到2时,则函数的值增加了2;
(2)解:在①,②,③,④中,
①③中对于x的每一个值,y都有唯一确定的值与它对应,②④中对于x的每一个值,y都有两个值与它对应,所以①③中是的函数,②④中不是的函数.
故答案为:①③.
22.(1)解:观察表中数据可知,当乘客量达到300人以上时,该公交车才不会亏损,票价为:600÷300=2(元/人);故答案为:300;2;
(2)由题意得:y=2x 600,∴公交车每天利润y(元)与每天乘车人数x(人)的关系式:y=2x 600,故答案为:2x 600;
(3)把y=1000代入y=2x 600中可得:2x 600=1000,解得:x=800,答:当乘车人数为800人时,利润为1000元.
23.解:(1)由图像可知,甲地与乙地相距1800千米,两车出发后4小时相遇;
故答案为:1800,4;
(2)由函数图像可知,普通列车12小时到达,则速度为1800÷12=150千米/小时
故答案为:12;150;.
(3)由题意得:动车的速度为: (km/h);
(4),
∴,,
∴点的坐标为.
24.
解:函数的自变量的取值范围是x≥1,函数的函数值
的取值范围是y≥0;
(2)解:如图所示:
(3)解:当时,,
故对应的函数值约为2.24;
(4)解:由图象可得:随的增大而增大.(答案不唯一)
一、单选题
1.下列表示y与x之间关系的图象中,y不是x的函数关系的是( )
A.B.C.D.
2.2022年春节期间,疫情形势复杂,张红遵循“防疫当前,本地过年”的原则,给远在家乡的家人打电话拜年.电话费随着时间的变化而变化,在这个过程中,因变量是( )
A.张红 B.电话费 C.时间 D.家人
3.在函数中,当自变量时,函数值等于( )
A.1 B.4 C.7 D.13
4.下面哪个点不在函数的图像上( )
A.(3,0) B.(0.5,2) C.(-5,13) D.(1,1)
5.如图,y=2x+10表示了自变量x与因变量y的关系,当x每增加1时,y增加( )
A.1 B.2 C.6 D.12
6.地表以下岩层的温度y()随着所处深度x()的变化而变化,在某个地点y与x之间的关系可以近似地用关系式来表示,也可用表格表示,其中表格的部分数据如下表所示,则其中的m,n分别是( )
1 2 4 m 9 10
55 n 160 230 335 370
A. B. C. D.
7.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.下图描述了他上学的情景,下列说法中正确的是( )
A.修车时间为15分钟 B.学校离家的距离为1000米
C.到达学校共用时间为10分钟 D.自行车发生故障时离家距离为1000米
8.如图,是某蓄水池的横断面示意图,蓄水池分为深水区和浅水区,如果向这个蓄水池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是( )
A.B.C. D.
9.用描点法画一次函数图象,在如表格中有一组数据错误,这组错误的数据是( )
x ﹣2 ﹣1 1 2
y 12 11 10 8
A.(﹣2,12) B.(﹣1,11) C.(1,10) D.(2,8)
10.在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是( )
A. B.
C. D.
二、填空题
11.函数的定义域为________.
12.变量,有如下关系:①;②.其中是的函数的是________.(填序号)
13.变量y与x之间的关系式为,当自变量时,因变量y的值为________.
14.小军用100元去买单价为5元的笔记本,他买完笔记本之后剩余的钱y元与买这种笔记本数量x本(,x为正整数)之间的关系式为______.
15.某文具店“六一”期间开展促销活动,销售总价与卖出笔记本数量的关系如表:
数量(件) 1 2 3 4 5 …
销售总价(元) 8 14 20 26 32 …
则售价与数量之间的关系式是______.
16.如表是加热食用油时温度随时间的变化情况:
时间 0 10 20 30 40
油温 10 30 50 70 90
王红发现,烧到时油沸腾了,则油的沸点是__________(沸点是指液体沸腾时候的温度).
17.根据如图所示的程序计算:若输入自变量x的值为,则输出的结果是_________________.
18.如图1,在长方形ABCD中,动点P从点B出发,沿方向匀速运动至点A停止,已知点P的运动速度为,设点P的运动时间为,的面积为,若关于的图像如图2所示,则长方形ABCD的面积为______.
三、解答题
19.已知一个长方形的长为x,宽为y,周长为40.
(1) 求出y关于x的函数解析式(不用写出自变量x的取值范围);
(2) 当时,求y的值;
(3) 当时,该长方形的面积是多少
20.如图1,在长方形ABCD中,点P从点B出发,沿B→C→D→A运动到点A停止.设点P的运动路程为x,△PAB的面积为y,y与x的关系图象如图2所示.
(1) AB的长度为______,BC的长度为______.
(2) 求图象中a和b的值.
(3) 在图象中,当m=15时,求n的值.
21.函数问题:
作出与的函数的图象
① 自变量的取值范围是____________;
② 列表并画出函数图象:
… 0 1 2 …
… …
③ 当自变量的值从1增加到2时,则函数的值增加了____________.
(2) 在一个变化的过程中,两个变量与之间可能是函数关系,也可能不是函数关系:
下列各式中, 是的函数的是____________.
①; ②; ③; ④;
22.某公交车每天的支出费用为600元,每天乘车人数
(人)与每天利润(利润=票款收入-支出费用)(元)的变化关系,如下表所示(每位乘客的乘车票价固定不变):
(人) … 200 250 300 350 400 …
(元) … -200 -100 0 100 200 …
根据表格中的数据,回答下列问题:
观察表中数据可知,当乘客量达到______人以上时,该公交车才不会亏损;票价为______(元/人);
请写出公交车每天利润(元)与每天乘车人数(人)的关系式:______;
当一天乘客人数为多少人时,利润是1000元?
23.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示)与x之间的函数关系.根据图象进行以下探究:
[信息读取]
(1)甲,乙两地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需______小时,普通列车的速度是______千米/小时:
[解决问题]
(3)求动车的速度:
(4)求点C的坐标.
24.小泽根据学习函数的经验,对函数的图象与性质进行了探究.下面是小泽的探究过程,请补充完成:
函数的自变量的取值范围是 ,函数值的取值范围是 ;
(2) 下表为与的几组对应值:
1 2 3 4 5
0 1 1.41 1.73 2
在所给的平面直角坐标系中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(3) 当时,对应的函数值约为 ;
(4) 结合图象写出该函数的一条性质: .
答案
一、单选题
1.C 2.B 3.C 4.A 5.B 6.D 7.D 8.C 9.C 10.D
二、填空题
11.x1
12.①
13.17
14.
15.y=2+6x
16.224
17.0.5
18.
三、解答题
19.
解:(1)∵长方形的周长为40,
∴2(x+y)=40,
∴y=-x+20;
(2)当x=13时,
y=20-13
=7;
(3)当y=8时,20-x=8,
∴x=12,
∴长方形的面积=12×8=96.
20.(1)解:由图2知,当x=5时,点P与C重合,
∴BC=5,
当x=13时,点P与D重合,
∴BC+CD=13,
∴CD=8=AB,
故答案为:8,5;
(2)当P与C点重合时,
=,
当点P与A重合时,
=5+8+5=18;
(3)∵,
∴此时点P在AD边上,且AP=3.
∴.
21.(1)解:①在函数中,x的取值范实为全体实数,
故答案为:全体实数;
②列表如下:
-2 -1 0 1 2
4 2 0 2 4
函数变形为或,画图如下:
③当时,,当时,,
所以当自变量的值从1增加到2时,则函数的值增加了2;
(2)解:在①,②,③,④中,
①③中对于x的每一个值,y都有唯一确定的值与它对应,②④中对于x的每一个值,y都有两个值与它对应,所以①③中是的函数,②④中不是的函数.
故答案为:①③.
22.(1)解:观察表中数据可知,当乘客量达到300人以上时,该公交车才不会亏损,票价为:600÷300=2(元/人);故答案为:300;2;
(2)由题意得:y=2x 600,∴公交车每天利润y(元)与每天乘车人数x(人)的关系式:y=2x 600,故答案为:2x 600;
(3)把y=1000代入y=2x 600中可得:2x 600=1000,解得:x=800,答:当乘车人数为800人时,利润为1000元.
23.解:(1)由图像可知,甲地与乙地相距1800千米,两车出发后4小时相遇;
故答案为:1800,4;
(2)由函数图像可知,普通列车12小时到达,则速度为1800÷12=150千米/小时
故答案为:12;150;.
(3)由题意得:动车的速度为: (km/h);
(4),
∴,,
∴点的坐标为.
24.
解:函数的自变量的取值范围是x≥1,函数的函数值
的取值范围是y≥0;
(2)解:如图所示:
(3)解:当时,,
故对应的函数值约为2.24;
(4)解:由图象可得:随的增大而增大.(答案不唯一)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
