八年级数学上册试题 5.5.4 一次函数中的动点问题-浙教版(含答案)
文档属性
| 名称 | 八年级数学上册试题 5.5.4 一次函数中的动点问题-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览



文档简介
5.5.4 一次函数中的动点问题
一、解答题
1.如图,在平面直角坐标系xOy中,一次函数与x轴、y轴分别交于点A、B两点,与正比例函数交于点D(2,2).
(1) 求一次函数和正比例函数的表达式;
(2) 若点P(m,m)为直线上的一个动点(点P不与点D重合),点Q在一次函数的图象上,轴,当PQ=OA时,求m的值.
2.综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
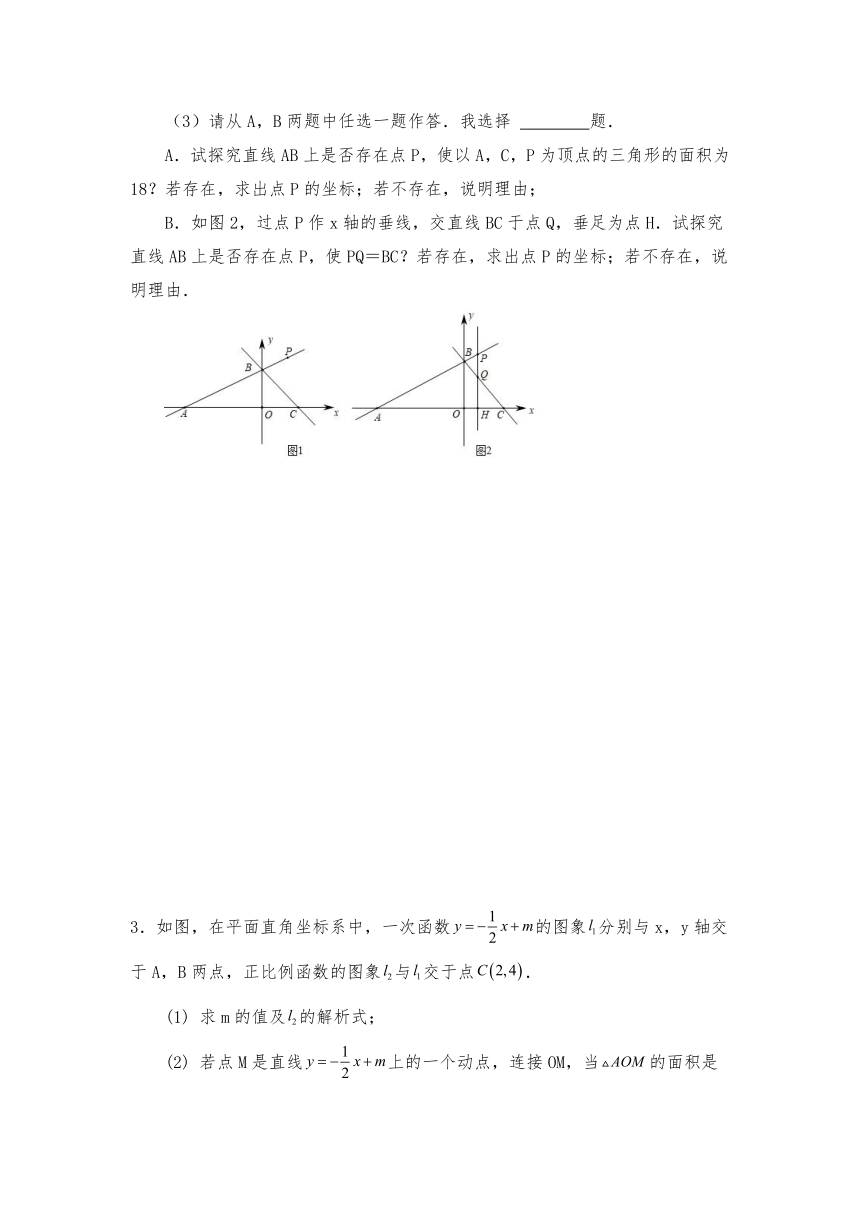
(3)请从A,B两题中任选一题作答.我选择 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
3.如图,在平面直角坐标系中,一次函数的图象分别与x,y轴交于A,B两点,正比例函数的图象与交于点.
(1) 求m的值及的解析式;
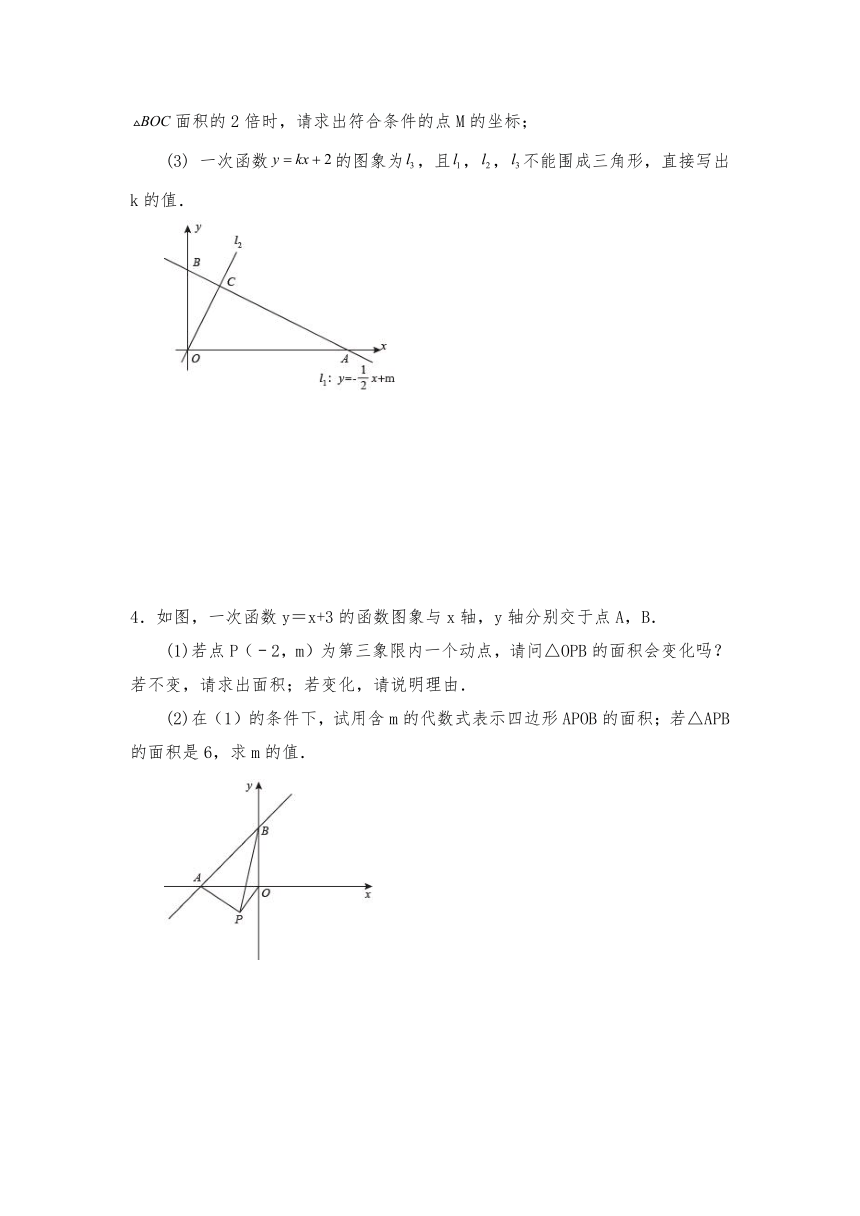
(2) 若点M是直线上的一个动点,连接OM,当的面积是面积的2倍时,请求出符合条件的点M的坐标;
(3) 一次函数的图象为,且,,不能围成三角形,直接写出k的值.
4.如图,一次函数y=x+3的函数图象与x轴,y轴分别交于点A,B.
(1)若点P(﹣2,m)为第三象限内一个动点,请问△OPB的面积会变化吗?若不变,请求出面积;若变化,请说明理由.
(2)在(1)的条件下,试用含m的代数式表示四边形APOB的面积;若△APB的面积是6,求m的值.
5.已知一次函数的图象经过A(2,4),B(﹣2,0)两点,且与y轴交于点C.求:
(1) 一次函数的解析式;
(2) △AOC的面积;
(3) 点D(m,0)是x轴上一个动点,过D作x轴的垂线,交直线AB于E,若DE=6,求m的值.
6.如图,一次函数与正比例函数的图象交于点B,与x轴交于点A.
(1) 求的面积;
(2) 观察图象,直接写出时,x的取值范围;
(3) 点C是直线OB上一动点,过点C作轴交直线AB于点D.当时,求点C的坐标.
7.如图,平面直角坐标系中,一次函数的图像与轴、轴分别交于点
,.点是线段上的一个动点(不与,重合),连接.设点的横坐标为.
(1) 求一次函数的解析式:
(2) 求的面积与之间的函数关系式,并写出自变量的取值范围;
(3) 当的面积时:
① 判断此时线段与的数量关系并说明理由;
② 第一象限内是否存在一点,使是以为直角边的等腰直角三角形,若存在,请直接写出点的坐标,若不存在,请说明理由.
8.如图,在平面直角坐标系中,一次函数的图像与x轴交于点,与一次函数的图像交于点.
(1)求一次函数的解析式;
(2)结合图像,当时,请直接写出x的取值范围;
(3)C为x轴上点A右侧一个动点,过点C作y轴的平行线,与一次函数的图像交于点D,与一次函数的图像交于点E.当时,求DE的长.
9.如图,一次函数y=﹣x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.
10.如图,一次函数的图象经过点和点,以线段为边在第二象限内作等腰直角,使.
(1) 求一次函数的表达式;
(2) 求出点的坐标;
(3) 若点是轴上一动点,直接写出的最小值.
11.如图,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为__.
12.在平面直角坐标系中,直线经过点与点,一次函数
的图象为直线.
(1)求此直线的解析式;
(2)过动点且垂直于轴的直线与的交点分别为,当点位于点上方时,请直接写出的取值范围
13.如图,一次函数的图像与轴,轴分别交于,两点.
(1) 求一次函数的解析式;
(2) 若为轴上一动点,当的面积为6时,求点的坐标.
14.如图,一次函数与x轴,y轴分别交于点A,B,点是直线AB
上一点,直线MC交x轴于点;
(1) 求直线MC的函数解析式;
(2) 若点P是线段AC上一动点,连接BP,MP,若的面积是面积的2倍,求P点坐标.
15.如图,一次函数的图象与x轴和y轴分别交于点A和点B,将△AOB沿直线CD对折,使点A和点B重合,直线CD与x轴交于点C,与AB交于点D.
(1) 求A,B两点的坐标;
(2) 求OC的长;
(3) 设P是x轴上一动点,若使△PAB是等腰三角形,写出点P的坐标(不需计算过程)
16.如图,平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A,B.点F是线段AB上的一个动点(不与A,B重合),连接OF,设点F的横坐标为x.
(1) 求A,B两点的坐标;
(2) 求△OAF的面积S与x之间的函数关系式:
(3) 当△OAF的面积时.直接写出线段OF与AB的数量关系;
17.平面直角坐标系中,一次函数的图象与轴交于点A,与轴交于点,与正比例函数的图象交于点.
(1) 求这两个函数的表达式;
(2) 在轴上有一动点,过点作直线垂直于轴,交直线于点,交直线于点.
① 当时,求的面积;
② 当的长为4时,求点的坐标.
18.如图,一次函数的图象与x轴和y轴分别交于点A和B,直线经过点B与点.
(1)求A、B点的坐标;
(2)求直线的表达式;
(3)在x轴上有一动点,过点M做x轴的垂线与直线交于点E,与直线交于点F,若EF=OB,求t的值.
19.如图,已知两个一次函数y1=x与y2=﹣2x﹣2的图象相交于点P.
(1)求点P的坐标;
(2)观察图象,直接写出当y1>y2时自变量x的取值范围;
(3)点A(t,0)为x轴上的一个动点,过点A作x轴的垂线与直线l1和l2分别交于点M,N,当MN=4时,求t的值.
20.如图,一次函数的图象与、轴分别交于、两点,点与点关于轴对称.动点、分别在线段,上(点与点,不重合),且满足.
(1)点的坐标为______,点的坐标为______,线段的长度______;
(2)当点在什么位置时,?说明理由;
(3)当为等腰三角形时,求点的坐标.
21.综合与探究:
如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
答案
一、解答题
1.
解:(1)∵一次函数与正比例函数交于点D(2,2),
∴,
∴,
∴一次函数解析式为:,正比例函数解析式为:;
(2)当x=0时,,
当y=0时,,即,
∴A点坐标为(3,0),B点坐标为(0,6),
∴OA=3,
∵PQ=OA,
∴PQ=,
∵轴,
∴点Q、点P的横坐标相等,
∵P点坐标为(m,m),
∴Q点的横坐标为m,
∵Q点在直线上,
∴,
∵轴,
∴,
∵,
∴,
解得:或者,
即m的值为或者.
2.
解:(1)当y=0时,x+3=0,解得x=﹣6,则A点坐标为(﹣6,0);
当x=0时,y=x+3=3,则B点坐标为(0,3);
(2)将B点坐标(0,3)代入一次函数y=﹣x+b得:b=3,
∴直线BC的表达式为y=﹣x+3,
当y=0时,﹣x+3=0,解得x=3,则C点坐标为(3,0);
(3)A.过点P作PH⊥x轴于H,
设点P(x,x+3),
∴PH=,
∵A点坐标为(﹣6,0),C点坐标(3,0),
∴AC=9,
∵S△ACP=AC PH=×9 PH=18,
∴PH=4,
∴x+3=±4,
当x+3=4时,x=2;当x+3=﹣4时,x=﹣14,
∴存在,点P的坐标为(2,4)或(﹣14,﹣4);
B.如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3),
∴PQ=,
∵B点坐标(0,3),C点坐标(3,0),
∴OB=OC=3,
∴BC=,
∵PQ=BC,
∴,解得:x=或﹣,
∴存在,点P的坐标为(2,+3)或(﹣2,﹣+3).
3.解:(1)与交于点.
设的解析式为,将点的坐标代入的解析式,可得,
,,
解得,,
的解析式为
(2)设,
,令,则,令,则
,
又
的面积是面积的2倍,
即
解得或
或
(3)一次函数的图象为,且,,不能围成三角形,
或
当过点C(2,4)时,将点C坐标代入y=kx+2并解得:k=l,
或或1
4.
(1)解:不变,理由是:
一次函数y=x+3的图象与x轴、y轴分别交于A、B,
则点A、B的坐标分别为(-3,0)、(0,3),
∴.
(2)解:∵
=
∴
=
解得m=-3.
5.(1)解:设该一次函数的解析式为:y=kx+b,
将A(2,4),B(﹣2,0)代入该一次函数解析式,得,
解得,
∴该一次函数的解析式为:y=x+2.
(2)解:如图,连接OA,过点A作AF⊥y轴于点F,
∵一次函数y=x+2与y轴交于点C,
∴C(0,2),
∴AF=2,OC=2,
∴S△AOC= AF OC=×2×2=2.
(3)解:∵DE⊥x轴,D(m,0),
∴E(m,m+2),
∴DE=|m+2|=6,
解得m=﹣8或4.
∴m的值为4或﹣8.
6.(1)解:令y1=-x+3中y=0,得x=3,∴A(3,0),
∴OA=3,
当-x+3=2x时,得x=1,
∴y=2,
∴B(1,2),
∴S△AOB=;
(2)由图象得:当x<1时,;
(3)设点C的坐标为(m,2m),
∵轴交直线AB于点D.
∴D(3-2m,2m),
∵,
∴CD=2,
∴,
解得m=或m=,
∴点C的坐标为(,)或(,).
7.(1)解:将点,点代入一次函数得:
,解得:,
∴一次函数的解析式为.
(2)解:∵点是线段上的一个动点(不与,重合),
设点的横坐标为,过点作轴,
∴点坐标为,
∴的面积:
,
∴的面积与之间的函数关系式为.
(3)解:①.理由如下:
当的面积时,
,
解得:,
∴F点坐标为,
∵轴,
∴在中,,
∵在中,,
∴.
②存在,点的坐标为或.
详解如下:过点作轴,过点作,过点作轴,分两种情况:
情况一:∵是等腰直角三角形
∴,
∴
∴
在和中
,
∴,
∴,,
∴,
∴,即;
情况二:∵是等腰直角三角形,
∴,,
∴,
∴,
在和中
,
∴,
∴,,
∴,
∴,
综上所述,点的坐标为或.
8.(1)解:当x=3时,y=x+2=4,
∴B点坐标为(3,4).
直线y1=kx+b经过A(5,0)和B(3,4),
则,
解得:,
∴一次函数y1=kx+b(k≠0)的解析式为y1=﹣2x+10;
(2)解:由图像以及B(3,4)可知,x<3时,y1>y2;
(3)解:设点C的横坐标为m,则D(m,﹣2m+10),E(m,m+2),
∴CE=m+2,CD=2m﹣10,
∵CE=3CD,
∴m+2=3(2m﹣10),解得m=6.
∴D(6,﹣2),E(6,6),
∴DE=8.
9.解:(1)一次函数y=﹣x+4的图象经过点A(m,2),
得﹣m+4=2,
解得m=,
∵一次函数y=﹣x+4的图象分别与x轴、y轴的正半轴交于点E,F.
∴当y=0时,﹣x+4=0,解得x=3即E(3,0);
当x=0时,y=4,即F(0,4);
(2)把点A(,2)一次函数y=kx﹣4,得2=k﹣4,解得k=4,
y=4x﹣4,当y=0时,x=1,即P(1,0).
PE=3﹣1=2,
S△APE=×2×2=2;
(3)存在Q点,B点是x轴上的动点,点Q是直线y=﹣x+4上的点,设Q(m,n).
由两点间的距离,得AE== ,AP==,PE=2.
①当点A与点B为对应顶点时,
∵△APE≌△BQE,
∴S△BQE=S△APE=2,
∴BE×|n|=2.
∵BE=AE=,
∴|n|=,n=±.
当n=时,﹣x+4=,解得m=,即Q1(,);
当n=﹣时,﹣x+4=﹣,解得m= ,即Q2(,﹣);
②当点A与点Q为对应顶点时,∵△APE≌△QBE,
则n=﹣2,把n=﹣2代入y=﹣x+4得m= ,
∴Q3(,﹣2),
综上所述:Q1(,),Q2(,﹣),Q3(,﹣2).
故答案为(1)m=,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(,),Q2(,﹣),Q3(,﹣2).
10.解:(1)由题意得:
将和点代入,
即:
,即,
;
(2)如图所示:
作轴,
,
在和中,
,
,
C点坐标为.
(3)作轴,并延长至点F使得,过F点作FH⊥y轴,垂足为H
连接交x轴与点P,此时有最小值即BF,
,
有最小值即.
11.解:∵一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,3),
∴OA=4,OB=3,
根据勾股定理可得AB==5,
如图1,当点A落在y轴的正半轴上时,
设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=3+5=8,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+82,
∴m=﹣6;
如图2,当点A落在y轴的负半轴上时,
设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=5﹣3=2,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+22,
∴m=;
综上所述,当点A落在y轴上时,点C的坐标为(﹣6,0)或(,0),
故答案为:(﹣6,0)或(,0).
12.解:(1)设直线的解析式为,
∵直线经过点A(1,5),B(4,2),
∴,
解得:,
∴直线的解析式为;
(2)联立,
解得:,
∵过动点且垂直于轴的直线与、的交点分别为C、D,如图:
观察图像可知当时,直线在直线上方,点位于点上方,
故答案为:.
13.(1)解:∵一次函数的图像与轴,轴分别交于,两点,∴,解得,一次函数的解析式为;
(2)解:设,,,,当的面积为6时,,解得或,或.
14.(1)解:把点代入得:
,
∴点M(1,3),
设直线MC的解析式为,
把点M(1,3),代入得:
,解得:,
∴直线MC的解析式为;
(2)解:对于,
当x=0时,y=2;当y=0时,x=-2,
∴点A(-2,0),B(0,2),
∴OA=OB=2,
设点P(a,0),则AP=a+2,PC=-a,
∵的面积是面积的2倍,
∴,
解得:,
∴点P的坐标为.
15.(1)解:令y=0,则x=4;令x=0,则y=3,
∴点A的坐标为(4,0),点B的坐标为(0,3).
(2)解:∵点B的坐标为(0,3).
∴OB=3,
设OC=x,则AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得x=,
∴OC=.
(3)解:∵点A的坐标为(4,0),点B的坐标为(0,3).
∴OA=4,OB=3,
∴AB=5,
设P点坐标为(x,0),则,,
当PA=PB时,,
解得x=;
当PA=AB时,,解得x=9或x=﹣1;
当PB=AB时,,解得x=﹣4或x=4(舍去).
∴P点坐标为(,0),(﹣4,0),(﹣1,0),(9,0).
16.解:(1)当时,,
当时,,
解得:,
点坐标为,点坐标为,
(2)点是线段上的一个动点(不与,重合),设点的横坐标为,
过点作轴,
点坐标为,
的面积,
即;
(3)OF=AB.理由如下:
当的面积时,
,
解得:,
点坐标为,
在中,,
在中,,
;
17.(1)解:∵正比例函数的图象过点,
,解得,
∴正比例函数的表达式为;
又∵一次函数的图象过点,
,
,
∴一次函数的表达式为;
(2)解:①根据题意得:点、点横坐标都为,且点G、F分别在直线,上,
∴点的坐标为,的坐标为,
,
;
②∵点,
∴点的纵坐标为,点的纵坐标为,
若点在点上方,
,
解得;
;
若点在点下方,
,
解得,
.
∴当的长为4时,点的坐标为或
18.(1)解:令x=0,则y=2,
令y=0,则,解得:x=-3,
∴点A(-3,0),B(0,2);
(2)解:把点B(0,2),代入,得:
,解得:,
∴直线的表达式为y=-x+2;
(3)解:∵点,
∴点,
∴,
∵点B(0,2),
∴OB=2,
∵EF=OB,
∴,解得:.
19.解:(1)联立,
解得:,
则点P坐标为(,);
(2)由图象可得,当y1>y2时,x>;
(3)设点M(t,t),N(t,-2t-2),
则MN=|t-(-2t-2)|=4,
解得:t=或t=-2.
20.解:(1)∵,
∴当x=0时,y=2,
当y=0时,x= 4,
即点A的坐标是( 4,0),点B的坐标是(0,2),
∵C点与A点关于y轴对称,
∴C的坐标是(4,0),
∴OA=4,OC=4,OB=2,
由勾股定理得:BC==2.
故答案为:( 4,0),(0,2),2.
(2)当P的坐标是(2 4,0)时,△APQ≌△CBP,
理由是:∵OA=4,P(2 4,0),
∴AP=4+2 4=2=BC,
∵∠BPQ=∠BAO,
∠BAO+∠AQP+∠APQ=180°,
∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
,
∴△APQ≌△CBP(AAS),
∴当P的坐标是(2 4,0)时,△APQ≌△CBP;
(3)分为三种情况:
①当PB=PQ时,由(2)知,△APQ≌△CBP,
∴PB=PQ,
即此时P的坐标是(2 4,0);
②当BQ=BP时,则∠BPQ=∠BQP,
∵∠BAO=∠BPQ,
∴∠BAO=∠BQP,
而根据三角形的外角性质得:∠BQP>∠BAO,
∴此种情况不存在;
③当QB=QP时,则∠BPQ=∠QBP=∠BAO,
即BP=AP,
设此时P的坐标是(x,0),
∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,
∴(x+4)2=x2+22,
解得:x= ,
即此时P的坐标是( ,0).
∴当△PQB为等腰三角形时,点P的坐标是(2 4,0)或( ,0).
21.(1)解:令y=0,则x+3=0,
∴x=﹣6,
∴A(﹣6,0),
令x=0,则y=3,
∴B(0,3),
∵一次函数y=﹣x+b的图象经过点B,
∴b=3,
∴y=﹣x+3,
令y=0,则x=3,
∴C(0,3);
(2)解:如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3)
∵B点坐标(0,3),C点坐标(3,0),
∴BC=3,
∵PQ=BC,
∴|x+3﹣(﹣x+3)|=3,
解得:x=2或﹣2,
∴存在,点P的坐标为(2,3)或(﹣2,3)
(3)解:存在,理由如下:
∵A(﹣6,0),B(0,3),
∴AB=3,
当以A为等腰三角形的顶点时,
AB=AM=3,
∴M(﹣6+3,0)或(﹣6﹣3,0);
②当以B为等腰三角形的顶点时,
AB=BM,
∴M点与A点关于y轴对称,
∴M(6,0);
③当以M为等腰三角形的顶点时,
MA=MB,
设M(m,0),
∴(m+6)2=m2+9,
∴m=﹣,
∴M(﹣,0);
综上所述:M点的坐标为(﹣6+3,0)或(﹣6﹣3,0)或(6,0)或(﹣,0).
一、解答题
1.如图,在平面直角坐标系xOy中,一次函数与x轴、y轴分别交于点A、B两点,与正比例函数交于点D(2,2).
(1) 求一次函数和正比例函数的表达式;
(2) 若点P(m,m)为直线上的一个动点(点P不与点D重合),点Q在一次函数的图象上,轴,当PQ=OA时,求m的值.
2.综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
3.如图,在平面直角坐标系中,一次函数的图象分别与x,y轴交于A,B两点,正比例函数的图象与交于点.
(1) 求m的值及的解析式;
(2) 若点M是直线上的一个动点,连接OM,当的面积是面积的2倍时,请求出符合条件的点M的坐标;
(3) 一次函数的图象为,且,,不能围成三角形,直接写出k的值.
4.如图,一次函数y=x+3的函数图象与x轴,y轴分别交于点A,B.
(1)若点P(﹣2,m)为第三象限内一个动点,请问△OPB的面积会变化吗?若不变,请求出面积;若变化,请说明理由.
(2)在(1)的条件下,试用含m的代数式表示四边形APOB的面积;若△APB的面积是6,求m的值.
5.已知一次函数的图象经过A(2,4),B(﹣2,0)两点,且与y轴交于点C.求:
(1) 一次函数的解析式;
(2) △AOC的面积;
(3) 点D(m,0)是x轴上一个动点,过D作x轴的垂线,交直线AB于E,若DE=6,求m的值.
6.如图,一次函数与正比例函数的图象交于点B,与x轴交于点A.
(1) 求的面积;
(2) 观察图象,直接写出时,x的取值范围;
(3) 点C是直线OB上一动点,过点C作轴交直线AB于点D.当时,求点C的坐标.
7.如图,平面直角坐标系中,一次函数的图像与轴、轴分别交于点
,.点是线段上的一个动点(不与,重合),连接.设点的横坐标为.
(1) 求一次函数的解析式:
(2) 求的面积与之间的函数关系式,并写出自变量的取值范围;
(3) 当的面积时:
① 判断此时线段与的数量关系并说明理由;
② 第一象限内是否存在一点,使是以为直角边的等腰直角三角形,若存在,请直接写出点的坐标,若不存在,请说明理由.
8.如图,在平面直角坐标系中,一次函数的图像与x轴交于点,与一次函数的图像交于点.
(1)求一次函数的解析式;
(2)结合图像,当时,请直接写出x的取值范围;
(3)C为x轴上点A右侧一个动点,过点C作y轴的平行线,与一次函数的图像交于点D,与一次函数的图像交于点E.当时,求DE的长.
9.如图,一次函数y=﹣x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.
10.如图,一次函数的图象经过点和点,以线段为边在第二象限内作等腰直角,使.
(1) 求一次函数的表达式;
(2) 求出点的坐标;
(3) 若点是轴上一动点,直接写出的最小值.
11.如图,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为__.
12.在平面直角坐标系中,直线经过点与点,一次函数
的图象为直线.
(1)求此直线的解析式;
(2)过动点且垂直于轴的直线与的交点分别为,当点位于点上方时,请直接写出的取值范围
13.如图,一次函数的图像与轴,轴分别交于,两点.
(1) 求一次函数的解析式;
(2) 若为轴上一动点,当的面积为6时,求点的坐标.
14.如图,一次函数与x轴,y轴分别交于点A,B,点是直线AB
上一点,直线MC交x轴于点;
(1) 求直线MC的函数解析式;
(2) 若点P是线段AC上一动点,连接BP,MP,若的面积是面积的2倍,求P点坐标.
15.如图,一次函数的图象与x轴和y轴分别交于点A和点B,将△AOB沿直线CD对折,使点A和点B重合,直线CD与x轴交于点C,与AB交于点D.
(1) 求A,B两点的坐标;
(2) 求OC的长;
(3) 设P是x轴上一动点,若使△PAB是等腰三角形,写出点P的坐标(不需计算过程)
16.如图,平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A,B.点F是线段AB上的一个动点(不与A,B重合),连接OF,设点F的横坐标为x.
(1) 求A,B两点的坐标;
(2) 求△OAF的面积S与x之间的函数关系式:
(3) 当△OAF的面积时.直接写出线段OF与AB的数量关系;
17.平面直角坐标系中,一次函数的图象与轴交于点A,与轴交于点,与正比例函数的图象交于点.
(1) 求这两个函数的表达式;
(2) 在轴上有一动点,过点作直线垂直于轴,交直线于点,交直线于点.
① 当时,求的面积;
② 当的长为4时,求点的坐标.
18.如图,一次函数的图象与x轴和y轴分别交于点A和B,直线经过点B与点.
(1)求A、B点的坐标;
(2)求直线的表达式;
(3)在x轴上有一动点,过点M做x轴的垂线与直线交于点E,与直线交于点F,若EF=OB,求t的值.
19.如图,已知两个一次函数y1=x与y2=﹣2x﹣2的图象相交于点P.
(1)求点P的坐标;
(2)观察图象,直接写出当y1>y2时自变量x的取值范围;
(3)点A(t,0)为x轴上的一个动点,过点A作x轴的垂线与直线l1和l2分别交于点M,N,当MN=4时,求t的值.
20.如图,一次函数的图象与、轴分别交于、两点,点与点关于轴对称.动点、分别在线段,上(点与点,不重合),且满足.
(1)点的坐标为______,点的坐标为______,线段的长度______;
(2)当点在什么位置时,?说明理由;
(3)当为等腰三角形时,求点的坐标.
21.综合与探究:
如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
答案
一、解答题
1.
解:(1)∵一次函数与正比例函数交于点D(2,2),
∴,
∴,
∴一次函数解析式为:,正比例函数解析式为:;
(2)当x=0时,,
当y=0时,,即,
∴A点坐标为(3,0),B点坐标为(0,6),
∴OA=3,
∵PQ=OA,
∴PQ=,
∵轴,
∴点Q、点P的横坐标相等,
∵P点坐标为(m,m),
∴Q点的横坐标为m,
∵Q点在直线上,
∴,
∵轴,
∴,
∵,
∴,
解得:或者,
即m的值为或者.
2.
解:(1)当y=0时,x+3=0,解得x=﹣6,则A点坐标为(﹣6,0);
当x=0时,y=x+3=3,则B点坐标为(0,3);
(2)将B点坐标(0,3)代入一次函数y=﹣x+b得:b=3,
∴直线BC的表达式为y=﹣x+3,
当y=0时,﹣x+3=0,解得x=3,则C点坐标为(3,0);
(3)A.过点P作PH⊥x轴于H,
设点P(x,x+3),
∴PH=,
∵A点坐标为(﹣6,0),C点坐标(3,0),
∴AC=9,
∵S△ACP=AC PH=×9 PH=18,
∴PH=4,
∴x+3=±4,
当x+3=4时,x=2;当x+3=﹣4时,x=﹣14,
∴存在,点P的坐标为(2,4)或(﹣14,﹣4);
B.如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3),
∴PQ=,
∵B点坐标(0,3),C点坐标(3,0),
∴OB=OC=3,
∴BC=,
∵PQ=BC,
∴,解得:x=或﹣,
∴存在,点P的坐标为(2,+3)或(﹣2,﹣+3).
3.解:(1)与交于点.
设的解析式为,将点的坐标代入的解析式,可得,
,,
解得,,
的解析式为
(2)设,
,令,则,令,则
,
又
的面积是面积的2倍,
即
解得或
或
(3)一次函数的图象为,且,,不能围成三角形,
或
当过点C(2,4)时,将点C坐标代入y=kx+2并解得:k=l,
或或1
4.
(1)解:不变,理由是:
一次函数y=x+3的图象与x轴、y轴分别交于A、B,
则点A、B的坐标分别为(-3,0)、(0,3),
∴.
(2)解:∵
=
∴
=
解得m=-3.
5.(1)解:设该一次函数的解析式为:y=kx+b,
将A(2,4),B(﹣2,0)代入该一次函数解析式,得,
解得,
∴该一次函数的解析式为:y=x+2.
(2)解:如图,连接OA,过点A作AF⊥y轴于点F,
∵一次函数y=x+2与y轴交于点C,
∴C(0,2),
∴AF=2,OC=2,
∴S△AOC= AF OC=×2×2=2.
(3)解:∵DE⊥x轴,D(m,0),
∴E(m,m+2),
∴DE=|m+2|=6,
解得m=﹣8或4.
∴m的值为4或﹣8.
6.(1)解:令y1=-x+3中y=0,得x=3,∴A(3,0),
∴OA=3,
当-x+3=2x时,得x=1,
∴y=2,
∴B(1,2),
∴S△AOB=;
(2)由图象得:当x<1时,;
(3)设点C的坐标为(m,2m),
∵轴交直线AB于点D.
∴D(3-2m,2m),
∵,
∴CD=2,
∴,
解得m=或m=,
∴点C的坐标为(,)或(,).
7.(1)解:将点,点代入一次函数得:
,解得:,
∴一次函数的解析式为.
(2)解:∵点是线段上的一个动点(不与,重合),
设点的横坐标为,过点作轴,
∴点坐标为,
∴的面积:
,
∴的面积与之间的函数关系式为.
(3)解:①.理由如下:
当的面积时,
,
解得:,
∴F点坐标为,
∵轴,
∴在中,,
∵在中,,
∴.
②存在,点的坐标为或.
详解如下:过点作轴,过点作,过点作轴,分两种情况:
情况一:∵是等腰直角三角形
∴,
∴
∴
在和中
,
∴,
∴,,
∴,
∴,即;
情况二:∵是等腰直角三角形,
∴,,
∴,
∴,
在和中
,
∴,
∴,,
∴,
∴,
综上所述,点的坐标为或.
8.(1)解:当x=3时,y=x+2=4,
∴B点坐标为(3,4).
直线y1=kx+b经过A(5,0)和B(3,4),
则,
解得:,
∴一次函数y1=kx+b(k≠0)的解析式为y1=﹣2x+10;
(2)解:由图像以及B(3,4)可知,x<3时,y1>y2;
(3)解:设点C的横坐标为m,则D(m,﹣2m+10),E(m,m+2),
∴CE=m+2,CD=2m﹣10,
∵CE=3CD,
∴m+2=3(2m﹣10),解得m=6.
∴D(6,﹣2),E(6,6),
∴DE=8.
9.解:(1)一次函数y=﹣x+4的图象经过点A(m,2),
得﹣m+4=2,
解得m=,
∵一次函数y=﹣x+4的图象分别与x轴、y轴的正半轴交于点E,F.
∴当y=0时,﹣x+4=0,解得x=3即E(3,0);
当x=0时,y=4,即F(0,4);
(2)把点A(,2)一次函数y=kx﹣4,得2=k﹣4,解得k=4,
y=4x﹣4,当y=0时,x=1,即P(1,0).
PE=3﹣1=2,
S△APE=×2×2=2;
(3)存在Q点,B点是x轴上的动点,点Q是直线y=﹣x+4上的点,设Q(m,n).
由两点间的距离,得AE== ,AP==,PE=2.
①当点A与点B为对应顶点时,
∵△APE≌△BQE,
∴S△BQE=S△APE=2,
∴BE×|n|=2.
∵BE=AE=,
∴|n|=,n=±.
当n=时,﹣x+4=,解得m=,即Q1(,);
当n=﹣时,﹣x+4=﹣,解得m= ,即Q2(,﹣);
②当点A与点Q为对应顶点时,∵△APE≌△QBE,
则n=﹣2,把n=﹣2代入y=﹣x+4得m= ,
∴Q3(,﹣2),
综上所述:Q1(,),Q2(,﹣),Q3(,﹣2).
故答案为(1)m=,E(3,0);F(0,4);(2)S△APE=2;(3)Q1(,),Q2(,﹣),Q3(,﹣2).
10.解:(1)由题意得:
将和点代入,
即:
,即,
;
(2)如图所示:
作轴,
,
在和中,
,
,
C点坐标为.
(3)作轴,并延长至点F使得,过F点作FH⊥y轴,垂足为H
连接交x轴与点P,此时有最小值即BF,
,
有最小值即.
11.解:∵一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,3),
∴OA=4,OB=3,
根据勾股定理可得AB==5,
如图1,当点A落在y轴的正半轴上时,
设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=3+5=8,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+82,
∴m=﹣6;
如图2,当点A落在y轴的负半轴上时,
设点C的坐标为(m,0),
∵将△ABC沿BC所在的直线折叠,当点A落在y轴上时,
∴A′O=5﹣3=2,A′C=AC=4﹣m,
∵A′C2=OC2+A′O2,
∴(4﹣m)2=m2+22,
∴m=;
综上所述,当点A落在y轴上时,点C的坐标为(﹣6,0)或(,0),
故答案为:(﹣6,0)或(,0).
12.解:(1)设直线的解析式为,
∵直线经过点A(1,5),B(4,2),
∴,
解得:,
∴直线的解析式为;
(2)联立,
解得:,
∵过动点且垂直于轴的直线与、的交点分别为C、D,如图:
观察图像可知当时,直线在直线上方,点位于点上方,
故答案为:.
13.(1)解:∵一次函数的图像与轴,轴分别交于,两点,∴,解得,一次函数的解析式为;
(2)解:设,,,,当的面积为6时,,解得或,或.
14.(1)解:把点代入得:
,
∴点M(1,3),
设直线MC的解析式为,
把点M(1,3),代入得:
,解得:,
∴直线MC的解析式为;
(2)解:对于,
当x=0时,y=2;当y=0时,x=-2,
∴点A(-2,0),B(0,2),
∴OA=OB=2,
设点P(a,0),则AP=a+2,PC=-a,
∵的面积是面积的2倍,
∴,
解得:,
∴点P的坐标为.
15.(1)解:令y=0,则x=4;令x=0,则y=3,
∴点A的坐标为(4,0),点B的坐标为(0,3).
(2)解:∵点B的坐标为(0,3).
∴OB=3,
设OC=x,则AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得x=,
∴OC=.
(3)解:∵点A的坐标为(4,0),点B的坐标为(0,3).
∴OA=4,OB=3,
∴AB=5,
设P点坐标为(x,0),则,,
当PA=PB时,,
解得x=;
当PA=AB时,,解得x=9或x=﹣1;
当PB=AB时,,解得x=﹣4或x=4(舍去).
∴P点坐标为(,0),(﹣4,0),(﹣1,0),(9,0).
16.解:(1)当时,,
当时,,
解得:,
点坐标为,点坐标为,
(2)点是线段上的一个动点(不与,重合),设点的横坐标为,
过点作轴,
点坐标为,
的面积,
即;
(3)OF=AB.理由如下:
当的面积时,
,
解得:,
点坐标为,
在中,,
在中,,
;
17.(1)解:∵正比例函数的图象过点,
,解得,
∴正比例函数的表达式为;
又∵一次函数的图象过点,
,
,
∴一次函数的表达式为;
(2)解:①根据题意得:点、点横坐标都为,且点G、F分别在直线,上,
∴点的坐标为,的坐标为,
,
;
②∵点,
∴点的纵坐标为,点的纵坐标为,
若点在点上方,
,
解得;
;
若点在点下方,
,
解得,
.
∴当的长为4时,点的坐标为或
18.(1)解:令x=0,则y=2,
令y=0,则,解得:x=-3,
∴点A(-3,0),B(0,2);
(2)解:把点B(0,2),代入,得:
,解得:,
∴直线的表达式为y=-x+2;
(3)解:∵点,
∴点,
∴,
∵点B(0,2),
∴OB=2,
∵EF=OB,
∴,解得:.
19.解:(1)联立,
解得:,
则点P坐标为(,);
(2)由图象可得,当y1>y2时,x>;
(3)设点M(t,t),N(t,-2t-2),
则MN=|t-(-2t-2)|=4,
解得:t=或t=-2.
20.解:(1)∵,
∴当x=0时,y=2,
当y=0时,x= 4,
即点A的坐标是( 4,0),点B的坐标是(0,2),
∵C点与A点关于y轴对称,
∴C的坐标是(4,0),
∴OA=4,OC=4,OB=2,
由勾股定理得:BC==2.
故答案为:( 4,0),(0,2),2.
(2)当P的坐标是(2 4,0)时,△APQ≌△CBP,
理由是:∵OA=4,P(2 4,0),
∴AP=4+2 4=2=BC,
∵∠BPQ=∠BAO,
∠BAO+∠AQP+∠APQ=180°,
∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
,
∴△APQ≌△CBP(AAS),
∴当P的坐标是(2 4,0)时,△APQ≌△CBP;
(3)分为三种情况:
①当PB=PQ时,由(2)知,△APQ≌△CBP,
∴PB=PQ,
即此时P的坐标是(2 4,0);
②当BQ=BP时,则∠BPQ=∠BQP,
∵∠BAO=∠BPQ,
∴∠BAO=∠BQP,
而根据三角形的外角性质得:∠BQP>∠BAO,
∴此种情况不存在;
③当QB=QP时,则∠BPQ=∠QBP=∠BAO,
即BP=AP,
设此时P的坐标是(x,0),
∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,
∴(x+4)2=x2+22,
解得:x= ,
即此时P的坐标是( ,0).
∴当△PQB为等腰三角形时,点P的坐标是(2 4,0)或( ,0).
21.(1)解:令y=0,则x+3=0,
∴x=﹣6,
∴A(﹣6,0),
令x=0,则y=3,
∴B(0,3),
∵一次函数y=﹣x+b的图象经过点B,
∴b=3,
∴y=﹣x+3,
令y=0,则x=3,
∴C(0,3);
(2)解:如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3)
∵B点坐标(0,3),C点坐标(3,0),
∴BC=3,
∵PQ=BC,
∴|x+3﹣(﹣x+3)|=3,
解得:x=2或﹣2,
∴存在,点P的坐标为(2,3)或(﹣2,3)
(3)解:存在,理由如下:
∵A(﹣6,0),B(0,3),
∴AB=3,
当以A为等腰三角形的顶点时,
AB=AM=3,
∴M(﹣6+3,0)或(﹣6﹣3,0);
②当以B为等腰三角形的顶点时,
AB=BM,
∴M点与A点关于y轴对称,
∴M(6,0);
③当以M为等腰三角形的顶点时,
MA=MB,
设M(m,0),
∴(m+6)2=m2+9,
∴m=﹣,
∴M(﹣,0);
综上所述:M点的坐标为(﹣6+3,0)或(﹣6﹣3,0)或(6,0)或(﹣,0).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
