八年级数学上册试题1.1认识三角形-三角形中的折叠问题同步练习-浙教版(含答案)
文档属性
| 名称 | 八年级数学上册试题1.1认识三角形-三角形中的折叠问题同步练习-浙教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 869.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 12:44:46 | ||
图片预览

文档简介
1.1认识三角形-三角形中的折叠问题
一、单选题
1.如图,把△ABC沿EF对折,折叠后的图形如图所示,,,则 的度数为( )
A. B. C. D.
2.如图,将沿翻折,三个顶点恰好落在点处.若,则的度数为( )
B.
C. D.
3.如图,在ABC中,∠ACB=90°,∠B-∠A=10°,D是AB上一点,将ACD沿CD翻折后得到CED,边CE交AB于点F.若DEF中有两个角相等,则∠ACD的度数为( )
A.15°或20°B.20°或30° C.15°或30° D.15°或25°
4.如图,中,,将沿折叠,使得点B落在边上的点F处,若且中有两个内角相等,则的度数为( )
A.30°或40° B.40°或50° C.50°或60° D.30°或60°
5.如图,中,分别是边上的点,连接,将沿着者折叠,得到,当的三边与的三边有一组边平行时,的度数不可能是( )
A. B. C. D.
6.如图,在中,,点为边上一动点,将沿着直线对折.若,则的度数为( )
A. B. C. D.
7.如图,和是分别沿着、边翻折形成的,若,则的度数为( )
A.100° B.90° C.85° D.80°
8.如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=82°,则原三角形的∠B的度数为( )
A.75° B.72° C.78° D.82°
9.如图,,是分别沿着边翻折形成的.若,与交于点,则的度数为( )
A.15° B.20° C.30° D.36°
10.如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=129°,则∠2的度数为( )
A.52° B.51° C.50° D.49°
11.如图,将纸片沿折叠,则( )
A. B.
C. D.
12.如图,在中,,将沿直线折叠,点C落在点D的位置,则的度数是( ).
A. B. C. D.无法确定
二、填空题
13.如图,在中,,,是线段上一个动点,连接,把沿折叠,点落在同一平面内的点处,当平行于的边时,的大小为______.
14.如图,将一张三角形纸片ABC的一角(∠A)折叠,使得点A落在四边形BCDE的外部点的位置,且点与点C在直线AB的异侧,折痕为DE.已知,,若的一边与BC平行,且,则m=______.
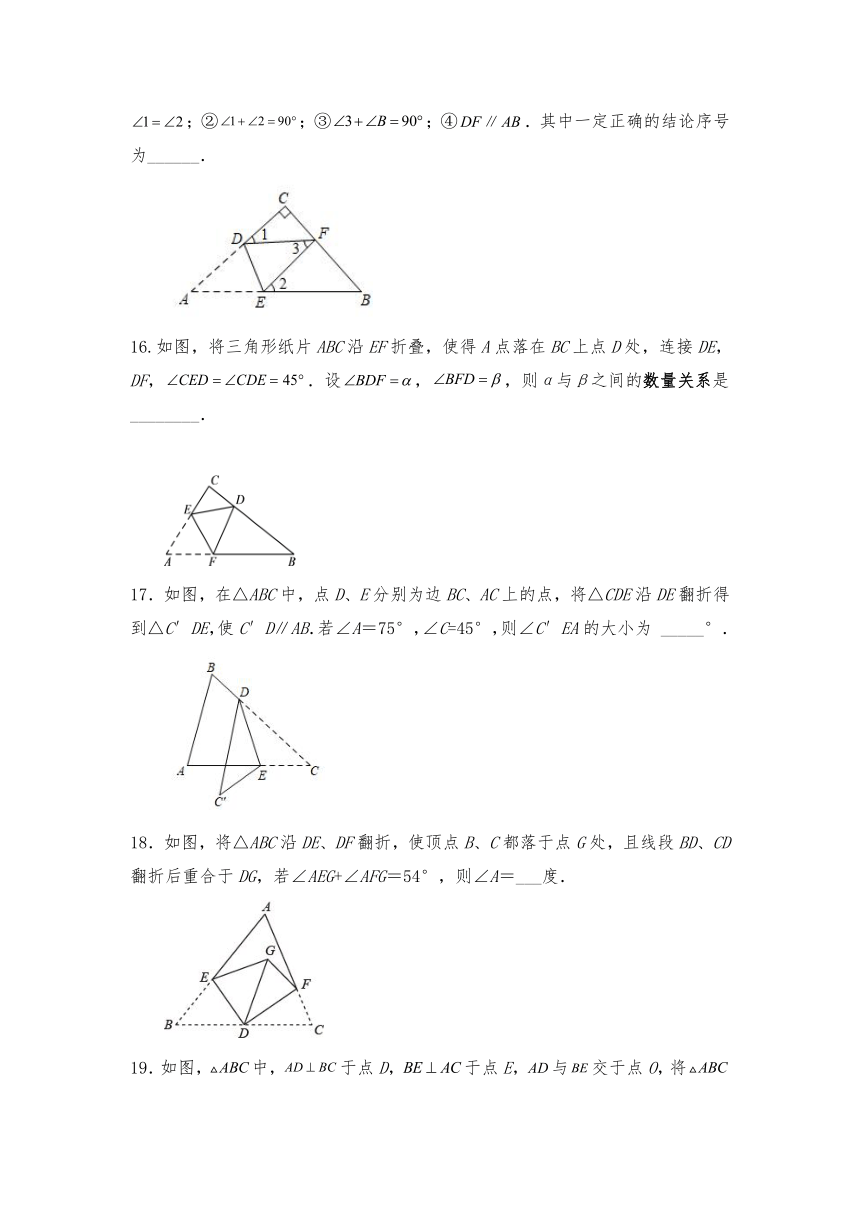
15.如图,为等腰直角三角形,,将按如图方式进行折叠,使点A与边上的点F重合,折痕分别与交于点D,点E.下列结论:①;②;③;④.其中一定正确的结论序号为______.
16.如图,将三角形纸片ABC沿EF折叠,使得A点落在BC上点D处,连接DE,DF,.设,,则α与β之间的数量关系是________.
17.如图,在△ABC中,点D、E分别为边BC、AC上的点,将△CDE沿DE翻折得到△C′DE,使C′D∥AB.若∠A=75°,∠C=45°,则∠C′EA的大小为 _____°.
18.如图,将△ABC沿DE、DF翻折,使顶点B、C都落于点G处,且线段BD、CD翻折后重合于DG,若∠AEG+∠AFG=54°,则∠A=___度.
19.如图,中,于点D,于点E,与交于点O,将沿折叠,使点C与点O重合,若,则__________.
20.如图,在中,,,将三角形沿对折,使点与边上的点重合.若,则的度数为____________.
21.如图,在△ABC中,∠A=42°,点D是边A上的一点,将△BCD沿直线CD翻折斜到△B′CD,B′C交AB于点E,如果B′D∥AC,那么∠BDC=___度.
22.如图,和是分别以、为对称轴翻折形成的,若,则的度数为_________.
三、解答题
23.如图,在中,点D为上一点,将沿翻折得到,与相交于点F,若平分,,.
(1)求证:;
(2)求的度数.
24.如图,在中,D、E分别是边AB、AC上一点,将沿DE折叠,使点A落在边BC上.若,求四个角和的度数?
25.如图是七年级下册数学教材第76页的部分内容.
请根据教材提示,结合图①,将证明过程补充完整.
【结论应用】
(1)如图②,在△中,∠=60°,平分∠,平分∠,求∠的度数.
(2)如图③,将△的∠折叠,使点落在△外的点处,折痕为.若∠=,∠=,∠=,则、、满足的等量关系为 (用、、的代数式表示).
26.如图,将一个直角三角形纸片,沿线段折叠,使点落在处,若,,求的度数.
27.如图,将一张三角形纸片的一角折叠,使得点A落在四边形的外部的位置且与点C在直线的异侧,折痕为,已知,.
(1)求的度数;
(2)若保持的一边与平行,求的度数.
答案
一、单选题
1.B 2.D 3.C 4.B 5.B 6.C 7.A
8.C 9.C 10.B 11.D 12.B
二、填空题
13.67°或118°
14.45或30
15.②③
16.
17.30
18.63
19.90
20.40°
21.111
22.80°
二、解答题
23.
(1)证明:∵,,
∴,
∵AE平分,
∴,
∵,
∴,
∴,
∴,
(2)解:,
∴,
∵,且,
∴.
24.
解:∵∠A=55°,
∴△ABC中,∠B+∠C=125°,
又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,
∴∠1+∠2+∠3+∠4=360°-(∠B+∠C)=360°-125°=235°.
25.
解:教材呈现:
∵CD∥BA,
∴∠1=∠ACD.
∵∠3+∠ACD+∠DCE=180°,,
∴.
结论应用:
(1)∵BP平分,CP平分,
∴,.
∵,,
∴.
∵,
∴.
(2)∵,
∴,
在△ABC中,,
又四边形BCDF内角和为360°,
∴,
∴.
26.解:,
,
,
∴∠ACB′=3∠B,
∵折叠,
∴,
,
,,
,即,
,
∴.
27.
解:(1)由折叠可知,
在中,
在中,
在四边形中,
因为
(2)①当时,
沿折叠
②当时,
由(1)知,,
,
沿折叠
综上,∠ADE的度数为:45°或30°.
一、单选题
1.如图,把△ABC沿EF对折,折叠后的图形如图所示,,,则 的度数为( )
A. B. C. D.
2.如图,将沿翻折,三个顶点恰好落在点处.若,则的度数为( )
B.
C. D.
3.如图,在ABC中,∠ACB=90°,∠B-∠A=10°,D是AB上一点,将ACD沿CD翻折后得到CED,边CE交AB于点F.若DEF中有两个角相等,则∠ACD的度数为( )
A.15°或20°B.20°或30° C.15°或30° D.15°或25°
4.如图,中,,将沿折叠,使得点B落在边上的点F处,若且中有两个内角相等,则的度数为( )
A.30°或40° B.40°或50° C.50°或60° D.30°或60°
5.如图,中,分别是边上的点,连接,将沿着者折叠,得到,当的三边与的三边有一组边平行时,的度数不可能是( )
A. B. C. D.
6.如图,在中,,点为边上一动点,将沿着直线对折.若,则的度数为( )
A. B. C. D.
7.如图,和是分别沿着、边翻折形成的,若,则的度数为( )
A.100° B.90° C.85° D.80°
8.如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=82°,则原三角形的∠B的度数为( )
A.75° B.72° C.78° D.82°
9.如图,,是分别沿着边翻折形成的.若,与交于点,则的度数为( )
A.15° B.20° C.30° D.36°
10.如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=129°,则∠2的度数为( )
A.52° B.51° C.50° D.49°
11.如图,将纸片沿折叠,则( )
A. B.
C. D.
12.如图,在中,,将沿直线折叠,点C落在点D的位置,则的度数是( ).
A. B. C. D.无法确定
二、填空题
13.如图,在中,,,是线段上一个动点,连接,把沿折叠,点落在同一平面内的点处,当平行于的边时,的大小为______.
14.如图,将一张三角形纸片ABC的一角(∠A)折叠,使得点A落在四边形BCDE的外部点的位置,且点与点C在直线AB的异侧,折痕为DE.已知,,若的一边与BC平行,且,则m=______.
15.如图,为等腰直角三角形,,将按如图方式进行折叠,使点A与边上的点F重合,折痕分别与交于点D,点E.下列结论:①;②;③;④.其中一定正确的结论序号为______.
16.如图,将三角形纸片ABC沿EF折叠,使得A点落在BC上点D处,连接DE,DF,.设,,则α与β之间的数量关系是________.
17.如图,在△ABC中,点D、E分别为边BC、AC上的点,将△CDE沿DE翻折得到△C′DE,使C′D∥AB.若∠A=75°,∠C=45°,则∠C′EA的大小为 _____°.
18.如图,将△ABC沿DE、DF翻折,使顶点B、C都落于点G处,且线段BD、CD翻折后重合于DG,若∠AEG+∠AFG=54°,则∠A=___度.
19.如图,中,于点D,于点E,与交于点O,将沿折叠,使点C与点O重合,若,则__________.
20.如图,在中,,,将三角形沿对折,使点与边上的点重合.若,则的度数为____________.
21.如图,在△ABC中,∠A=42°,点D是边A上的一点,将△BCD沿直线CD翻折斜到△B′CD,B′C交AB于点E,如果B′D∥AC,那么∠BDC=___度.
22.如图,和是分别以、为对称轴翻折形成的,若,则的度数为_________.
三、解答题
23.如图,在中,点D为上一点,将沿翻折得到,与相交于点F,若平分,,.
(1)求证:;
(2)求的度数.
24.如图,在中,D、E分别是边AB、AC上一点,将沿DE折叠,使点A落在边BC上.若,求四个角和的度数?
25.如图是七年级下册数学教材第76页的部分内容.
请根据教材提示,结合图①,将证明过程补充完整.
【结论应用】
(1)如图②,在△中,∠=60°,平分∠,平分∠,求∠的度数.
(2)如图③,将△的∠折叠,使点落在△外的点处,折痕为.若∠=,∠=,∠=,则、、满足的等量关系为 (用、、的代数式表示).
26.如图,将一个直角三角形纸片,沿线段折叠,使点落在处,若,,求的度数.
27.如图,将一张三角形纸片的一角折叠,使得点A落在四边形的外部的位置且与点C在直线的异侧,折痕为,已知,.
(1)求的度数;
(2)若保持的一边与平行,求的度数.
答案
一、单选题
1.B 2.D 3.C 4.B 5.B 6.C 7.A
8.C 9.C 10.B 11.D 12.B
二、填空题
13.67°或118°
14.45或30
15.②③
16.
17.30
18.63
19.90
20.40°
21.111
22.80°
二、解答题
23.
(1)证明:∵,,
∴,
∵AE平分,
∴,
∵,
∴,
∴,
∴,
(2)解:,
∴,
∵,且,
∴.
24.
解:∵∠A=55°,
∴△ABC中,∠B+∠C=125°,
又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,
∴∠1+∠2+∠3+∠4=360°-(∠B+∠C)=360°-125°=235°.
25.
解:教材呈现:
∵CD∥BA,
∴∠1=∠ACD.
∵∠3+∠ACD+∠DCE=180°,,
∴.
结论应用:
(1)∵BP平分,CP平分,
∴,.
∵,,
∴.
∵,
∴.
(2)∵,
∴,
在△ABC中,,
又四边形BCDF内角和为360°,
∴,
∴.
26.解:,
,
,
∴∠ACB′=3∠B,
∵折叠,
∴,
,
,,
,即,
,
∴.
27.
解:(1)由折叠可知,
在中,
在中,
在四边形中,
因为
(2)①当时,
沿折叠
②当时,
由(1)知,,
,
沿折叠
综上,∠ADE的度数为:45°或30°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
