浙教版九年级数学下册3.1直线和圆的位置关系
文档属性
| 名称 | 浙教版九年级数学下册3.1直线和圆的位置关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 126.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-03 23:19:00 | ||
图片预览


文档简介
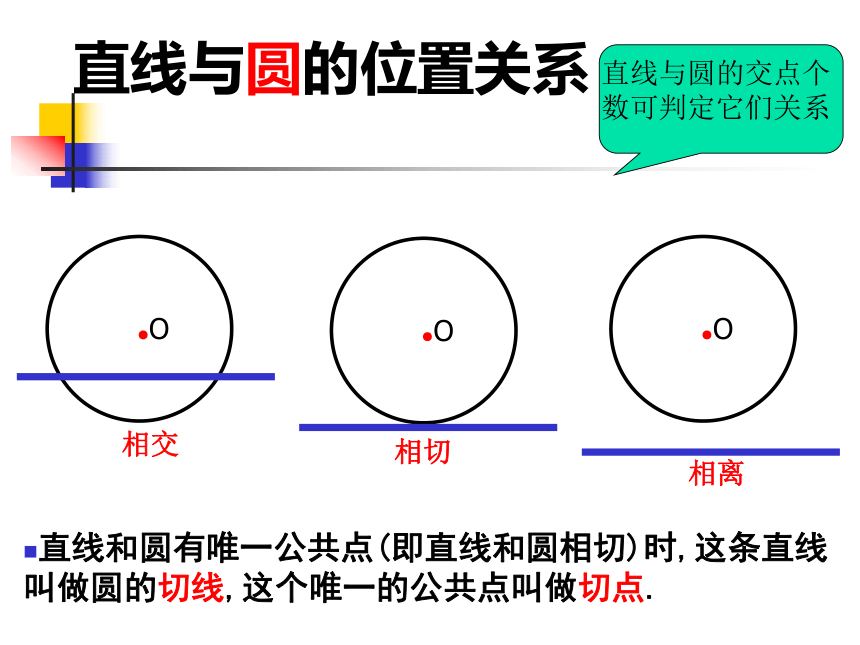
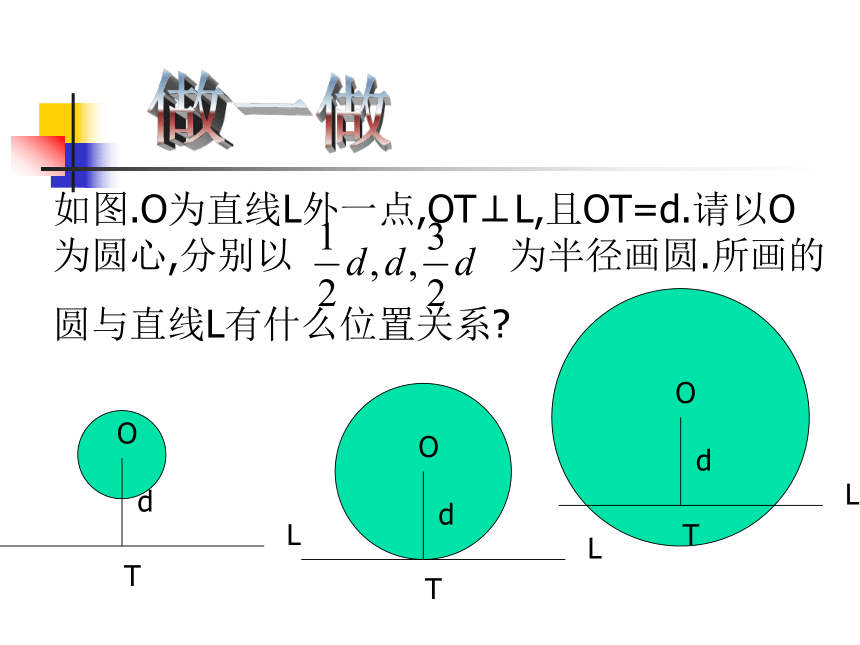
课件12张PPT。3.1直线与圆的位置关系海上日出直线与圆的位置关系相交直线和圆有唯一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.相切相离做一做如图.O为直线L外一点,OT⊥L,且OT=d.请以O为圆心,分别以 为半径画圆.所画的
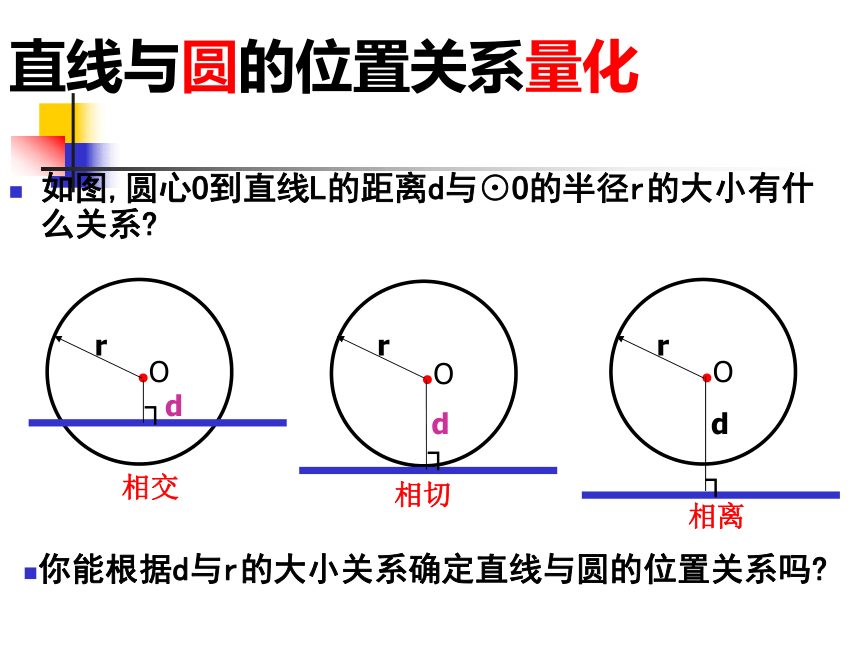
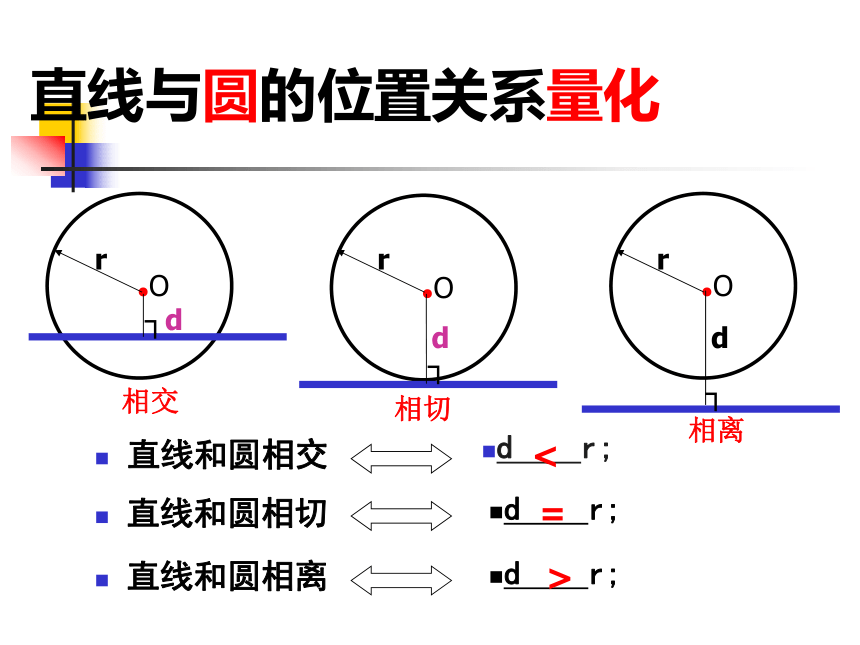
圆与直线L有什么位置关系?如图,圆心O到直线L的距离d与⊙O的半径r的大小有什么关系? 你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化<=>练一练 设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:
d=4,r=3 (2)d=1,r= (3)
(4)解:(1)∵d>r,
∴直线 与⊙O相离.(2)∵d ∴直线 与⊙O相交.(4)∵d=r,
∴直线 与⊙O相切.(3)∵d>r,
∴直线 与⊙O相离. 已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.以点C为圆心作圆,当半径为多长时,AB与⊙C相切?例1;解:作CD⊥AB于点D.∵S△ABC=AC×BC÷2=AB×CD÷284∴CD=AC×BC÷AB=∴ AB与⊙C相切.在直角三角形ABC 中,∠ACB=90°,CA=3,CB=4.设⊙C 的半径为r. 请根据r的下列值,判断AB与⊙C 的位置关系,并说明理由.
(1) r=2 (2) r=2.4 (3) r=3练一练34解:作CD⊥AB于点D.AB=5, CD=3×4÷5=2.4(1)∵r<CD, ∴直线AB与⊙C相离.(2)∵r=CD, ∴直线AB与⊙C相切.(3)∵r>CD, ∴直线AB与⊙C相交.1、船有无触礁的危险如图,海中有一个小岛P,该岛四周12海里内暗礁.今有一货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行.请与同伴交流你是怎么想的? 怎么去做?你认为货轮继续向东航行途中会有触礁的危险吗?PABH北例2;60045010解:作PH⊥AB于点H.由题可得 ∠PAH=30○ , ∠PBH=45○∴货轮没有触礁的危险。PABH北60045010如图,海中有一个小岛P,该岛四周12海里内暗礁.今有一货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航 行.你认为货轮继续向东航行途中会有触礁的危险吗?
直线和圆的位置关系210dr交点切点无 割线 切线 无O?drOl?dr
圆与直线L有什么位置关系?如图,圆心O到直线L的距离d与⊙O的半径r的大小有什么关系? 你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化<=>练一练 设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:
d=4,r=3 (2)d=1,r= (3)
(4)解:(1)∵d>r,
∴直线 与⊙O相离.(2)∵d
∴直线 与⊙O相切.(3)∵d>r,
∴直线 与⊙O相离. 已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.以点C为圆心作圆,当半径为多长时,AB与⊙C相切?例1;解:作CD⊥AB于点D.∵S△ABC=AC×BC÷2=AB×CD÷284∴CD=AC×BC÷AB=∴ AB与⊙C相切.在直角三角形ABC 中,∠ACB=90°,CA=3,CB=4.设⊙C 的半径为r. 请根据r的下列值,判断AB与⊙C 的位置关系,并说明理由.
(1) r=2 (2) r=2.4 (3) r=3练一练34解:作CD⊥AB于点D.AB=5, CD=3×4÷5=2.4(1)∵r<CD, ∴直线AB与⊙C相离.(2)∵r=CD, ∴直线AB与⊙C相切.(3)∵r>CD, ∴直线AB与⊙C相交.1、船有无触礁的危险如图,海中有一个小岛P,该岛四周12海里内暗礁.今有一货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行.请与同伴交流你是怎么想的? 怎么去做?你认为货轮继续向东航行途中会有触礁的危险吗?PABH北例2;60045010解:作PH⊥AB于点H.由题可得 ∠PAH=30○ , ∠PBH=45○∴货轮没有触礁的危险。PABH北60045010如图,海中有一个小岛P,该岛四周12海里内暗礁.今有一货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航 行.你认为货轮继续向东航行途中会有触礁的危险吗?
直线和圆的位置关系210d
