7.4 一次函数的图象(1)

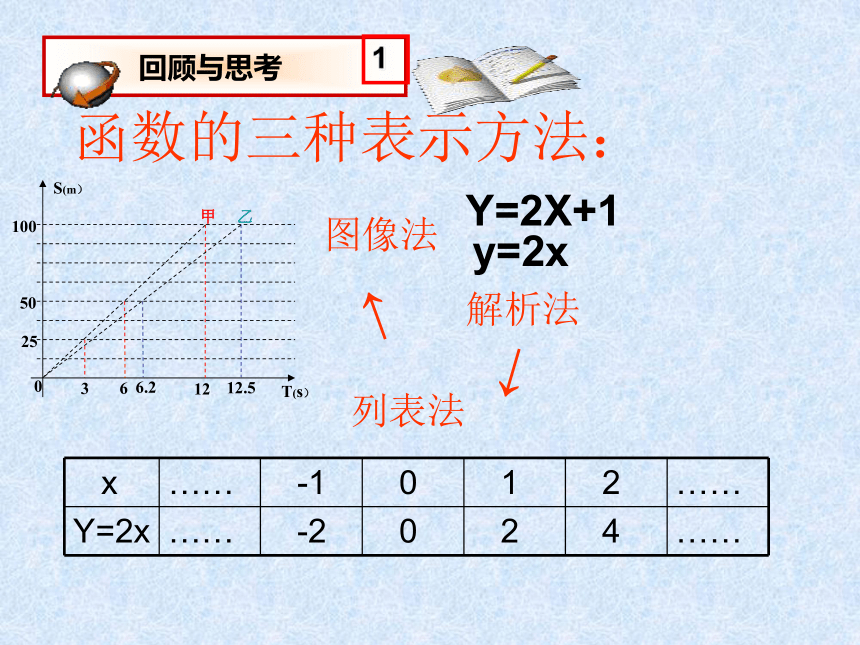
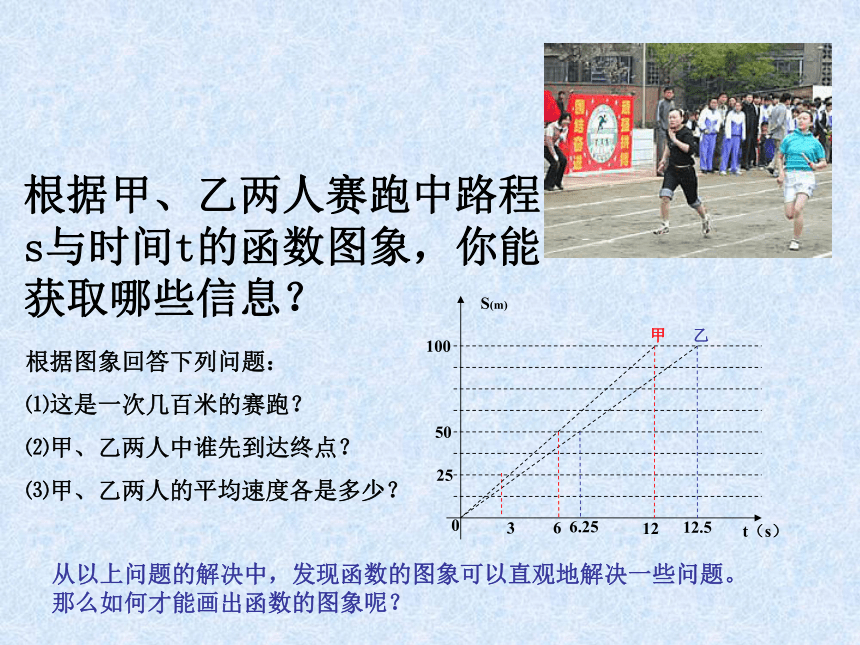
课件16张PPT。函数的三种表示方法：图像法列表法解析法↓↓根据甲、乙两人赛跑中路程s与时间t的函数图象，你能获取哪些信息？根据图象回答下列问题：
⑴这是一次几百米的赛跑？
⑵甲、乙两人中谁先到达终点？
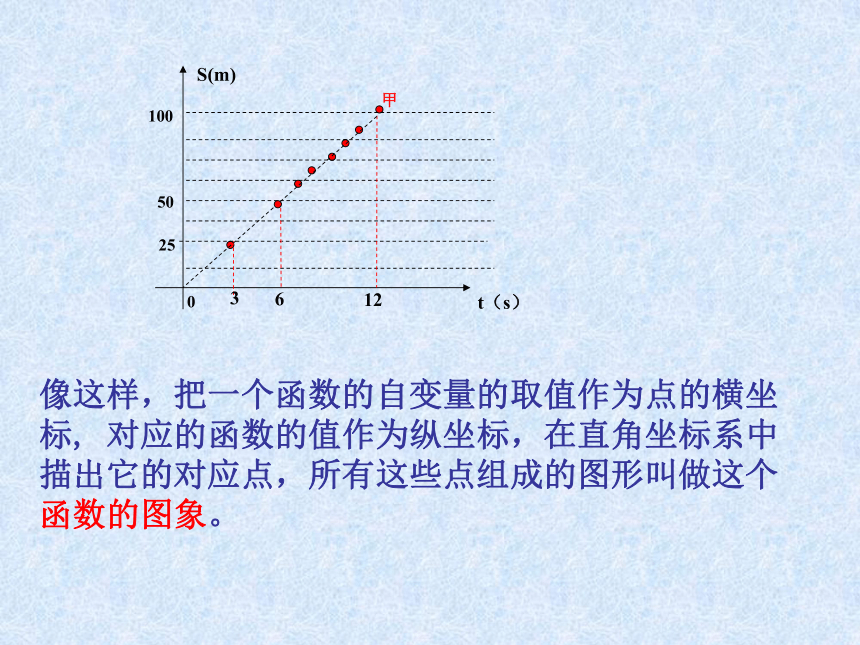
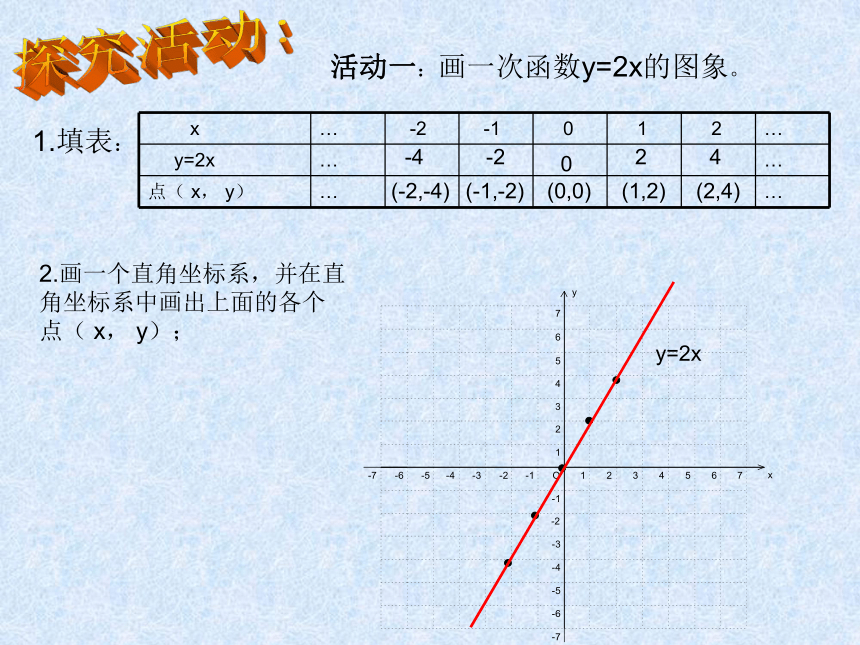
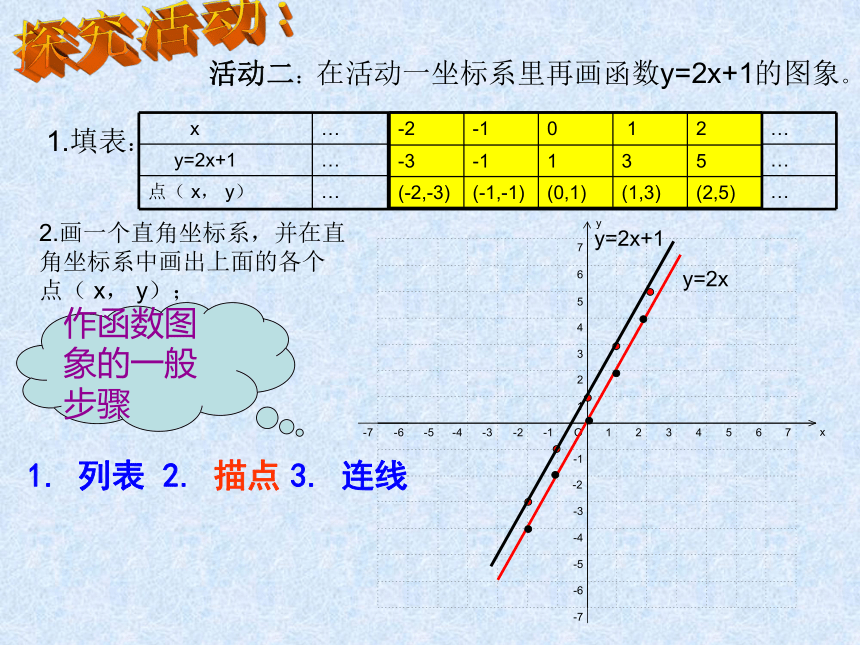
⑶甲、乙两人的平均速度各是多少？从以上问题的解决中，发现函数的图象可以直观地解决一些问题。那么如何才能画出函数的图象呢？7.4.1一次函数的图象像这样，把一个函数的自变量的取值作为点的横坐标, 对应的函数的值作为纵坐标，在直角坐标系中描出它的对应点，所有这些点组成的图形叫做这个函数的图象。0探究活动:活动一：画一次函数y=2x的图象。 1.填表： 2.画一个直角坐标系，并在直
角坐标系中画出上面的各个
点（ x， y）； -4(-2,-4)-2(-1,-2)0(0,0)2(1,2)4(2,4)y=2x探究活动:活动二：在活动一坐标系里再画函数y=2x+1的图象。 1.填表： 2.画一个直角坐标系，并在直
角坐标系中画出上面的各个
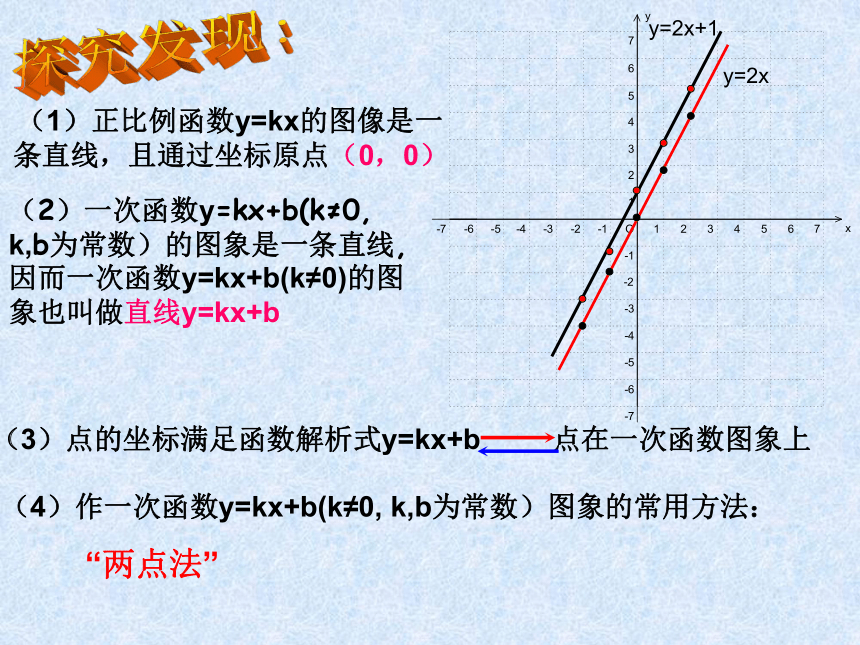
点（ x， y）； y=2x+1作函数图象的一般步骤1. 列表2. 描点 3. 连线y=2xy=2x+1y=2x探究发现:（1）正比例函数y=kx的图像是一条直线，且通过坐标原点（0，0）（2）一次函数y=kx+b(k≠0, k,b为常数）的图象是一条直线, 因而一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b（4）作一次函数y=kx+b(k≠0, k,b为常数）图象的常用方法：“两点法”YXOY=3XY=-3X+6 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8例题
(1)在同一坐标系作出下列函数的图象
y=3x, y=-3x+6YXOY=3X -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8（2）若y=3x表示一辆汽车以3米秒的速度行驶x秒后，路程为y米，则它的图像还和刚才一样吗？为什么？y=3x(x≥0)y=3x (x≥0)YXOY=-3X+6 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8(3) 已知点（a，-6）在直线y=-3x+6图象上，则a为多少?
YXOY=3XY=-3X+6 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8（4）求出直线y=3x与坐标轴的交点坐标,直线y=-3x+6与坐标轴的交点坐标。练习:求直线y=2x-4与坐标轴的交点坐标解：令x＝０，则y＝－４∴直线y=2x-4与y轴交点坐标为（０，－４）令y＝０，得：2x-4＝０即：x＝２∴直线y=2x-4与Ｘ轴交点坐标为（２，０）
熟能生巧:本节课你学到了什么? 2、函数图象的概念包含两个方面的内容：
点的坐标满足函数解析式 点在此函数图像上1、函数图象的概念3、作函数图象的一般步骤：
（1）列表；　（2）描点；（3）连线
4、一次函数的图象特征和常用画法5、一次函数y=kx+b（k≠0）与坐标轴的交点坐标几个知识点两个注意1、当自变量取任意实数时，一次函数的图象是一条直线2、画函数图象时还应特别注意：需考虑自变量的取值范围。数形结合思想方法— “数”用“形”表示，由“形”想到“数”一种数学思想作业
作业本(2): 7.4一次函数的图象(1)
YXOY=3XY=-3X+6 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8你能求出直线y=3X与直线y=-3X+6的交点坐标吗？思考题：