1.3 二次根式的运算(3)(浙江省金华市婺城区)
文档属性
| 名称 | 1.3 二次根式的运算(3)(浙江省金华市婺城区) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-12 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
教 师 备 课 笔 记
上课日期 月 日 星期
课题 1.3 二次根式的运算(3) 课型 新授
教学目标 熟练地运用二次根式的性质化简二次根式;会运用二次根式解决简单的实际问题;进一步体验二次根式及其运算的实际意义和应用价值。
重点和难点 重点:本节教学的重点是二次根式及其运算的实际应用.难点:课本上的例7涉及多方面的知识和综合运用,思路比较复杂,是本节教学的难点
教具准备 三角板、多媒体课件
师 生 活 动 过 程
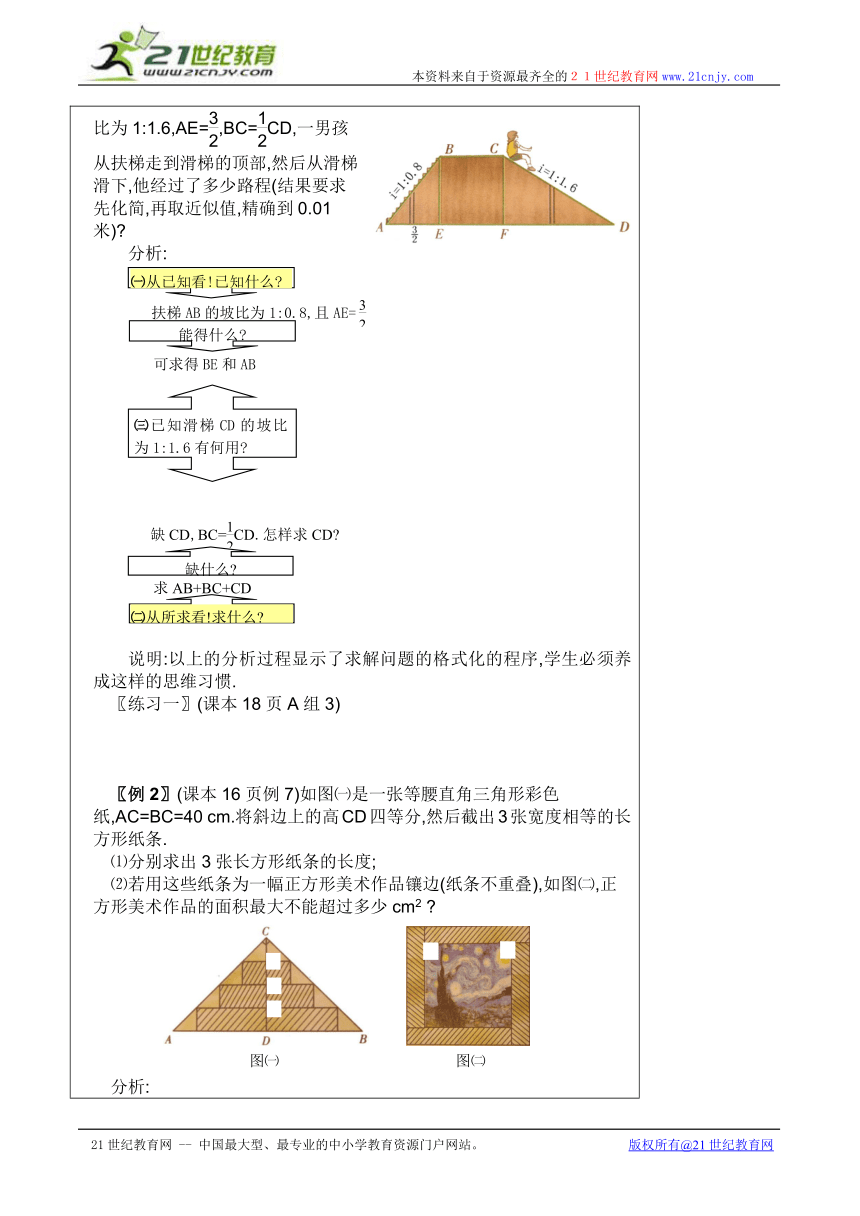
一、创设情境,引入课题二次根式的知识在实际生活中有广泛的用途.如图,我们规定斜坡的铅直高h与水平长度l的比叫做坡比(或坡度),即:坡比 i= 已知斜坡的坡比为3:4,且其高CE=2dm,宽AB=1dm.一只蚂蚁从A点爬到C点,最短路程多少 说明:设计本题有以下目的:⑴介绍预备知识“坡比”;⑵激发学生的兴趣;⑶会用二次根式表示未知量.在Rt△BCE中,BC的长宜直接表示为:BC=;⑷建议用多媒体播放此题目和图片,教师引导学生分析,解答过程宜板书而弃PowerPoint.以下例题同.〖初步体验〗(课本17页课内练习1)二、应用举例〖例1〗(课本15页例6)如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=,BC=CD,一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他经过了多少路程(结果要求先化简,再取近似值,精确到0.01米) 分析:说明:以上的分析过程显示了求解问题的格式化的程序,学生必须养成这样的思维习惯.〖练习一〗(课本18页A组3)〖例2〗(课本16页例7)如图㈠是一张等腰直角三角形彩色纸,AC=BC=40 cm.将斜边上的高CD四等分,然后截出3张宽度相等的长方形纸条.
⑴分别求出3张长方形纸条的长度;
⑵若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图㈡,正方形美术作品的面积最大不能超过多少cm2 分析:⑴①如图㈠,从已知能得什么 在Rt△ABC中,CD⊥,AC=BC=40,易求得AB和CD长(让学生求),则CE3 =E3F3 =F3G3 =G3D = CD,纸条的宽度可求.②怎样求纸条的长度 纸条的总长度=E1E2+F1F2+G1G2 ,如怎样求E1E2(让学生想一想) E1E2 =2CE3.,F1F2和G1G2 呢 同理,F1F2=2CF3 ,G1G2=2CG3 .⑵如图㈡,由⑴得纸条的总长度为60,它被四等分,每条长AC=15,它们所围成的正方形的边长AB多少 AB=AC–BC=10 .〖练习二〗(课本18页B组4)三、小结:谈一谈:本节课你有什么收获?运用二次根式解决简单的实际问题时应注意的的问题四、布置作业1: 作业本(2)2:课本P17页:作业题第1、2、3题,第4、5题选做。
教后随笔
教 师 备 课 笔 记
上课日期 月 日 星期
课题 5.1 多边形(3) 课型 新授
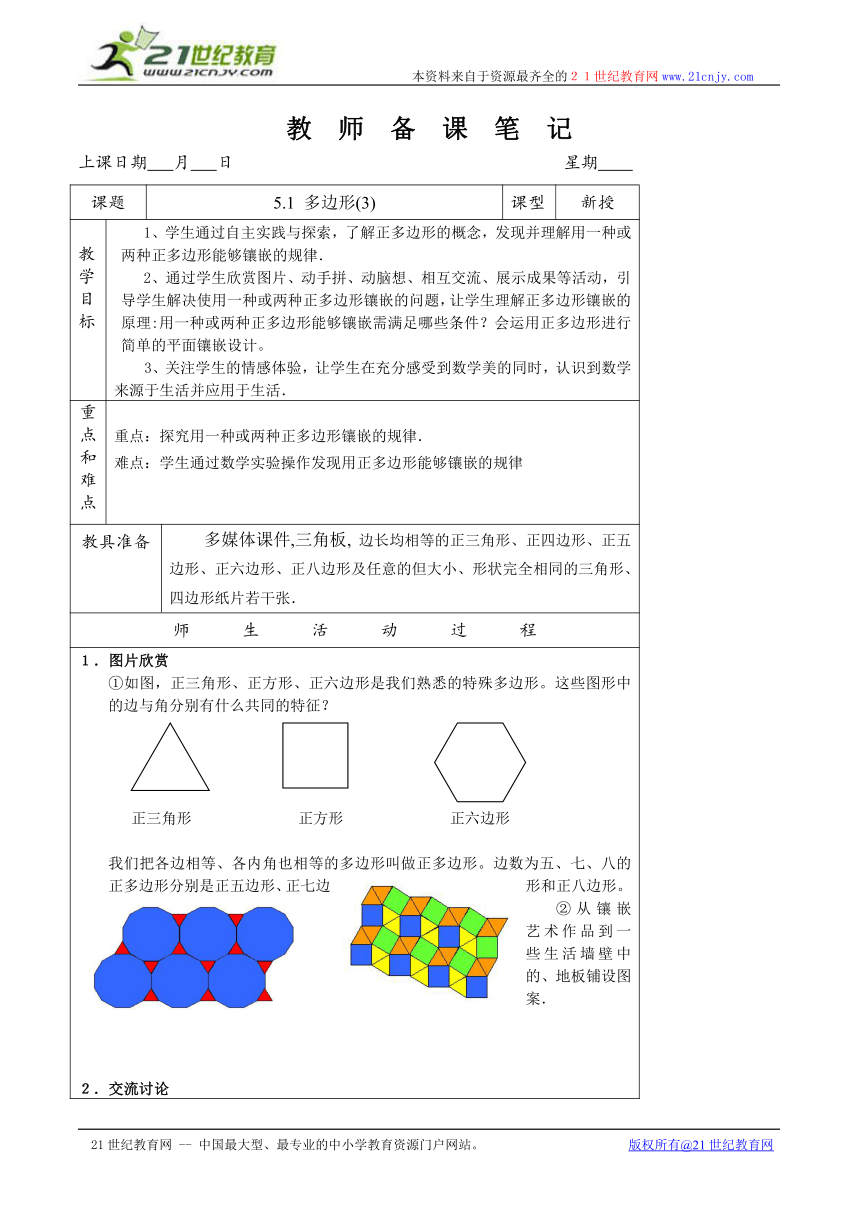
教学目标 1、学生通过自主实践与探索,了解正多边形的概念,发现并理解用一种或两种正多边形能够镶嵌的规律.2、通过学生欣赏图片、动手拼、动脑想、相互交流、展示成果等活动,引导学生解决使用一种或两种正多边形镶嵌的问题,让学生理解正多边形镶嵌的原理:用一种或两种正多边形能够镶嵌需满足哪些条件?会运用正多边形进行简单的平面镶嵌设计。3、关注学生的情感体验,让学生在充分感受到数学美的同时,认识到数学来源于生活并应用于生活.
重点和难点 重点:探究用一种或两种正多边形镶嵌的规律.难点:学生通过数学实验操作发现用正多边形能够镶嵌的规律
教具准备 多媒体课件,三角板, 边长均相等的正三角形、正四边形、正五边形、正六边形、正八边形及任意的但大小、形状完全相同的三角形、四边形纸片若干张.
师 生 活 动 过 程
1.图片欣赏①如图,正三角形、正方形、正六边形是我们熟悉的特殊多边形。这些图形中的边与角分别有什么共同的特征? 正三角形 正方形 正六边形 我们把各边相等、各内角也相等的多边形叫做正多边形。边数为五、七、八的正多边形分别是正五边形、正七边形和正八边形。②从镶嵌艺术作品到一些生活墙壁中的、地板铺设图案.2.交流讨论学生直观感受数学美的同时,引导学生思考:这些图案都是由哪些基本的平面图形构成的?(正三角形、正方形、正五边形、正六边形)学生细心观察后发现,图案中的平面图形有的规则,有的不规则;有的用一种多边形拼成,有的用多种多边形拼成,培养学生分类的思想.3.感知概念讨论这些图形拼成一个平面的共同特征,注意到各图形之间没有空隙,也没有重叠.在充分交流的基础上,用自己的语言概括镶嵌的概念(象这种既无缝隙又不重叠的铺法,我们称为平面的镶嵌).教师给予鼓励和评价.4.提出问题提问:如果让你们设计几种地板图案,需要解决什么问题?学生自主探索,分组研究需要探讨的问题,教师做适当引导.把其中可能列举的典型问题设想如下:(1) 怎样铺设可以不留空隙,也不相互重叠?(2) 可以用哪些图形?(3) 用前面所学的正多边形能否拼成一个平面图形?(4) 哪些正多边形可以镶嵌成一个平面,哪些不能? 根据学生提出的以及本节课需要解决的问题,首先引导学生研究最简单的镶嵌问题.5、探索仅用一种多边形镶嵌,哪些正多边形可以镶嵌成一个片面图案.(1)动手实验全班分成九个小组,拿出课前准备好的正三角形、正四边形、正五边形、正六边形,以小组为单位进行比赛,看哪个小组拼得又快又好,并派代表在投影仪上展示他们的成果.收集数据根据刚才的动手实验,引导学生收集数据,观察结果.正n边形每个内角的度数使用正多边形的个数结果n =360°6能拼好n = 490°4能拼好n = 5108°3不能拼好,有缺口4不能拼好,有重叠n = 6120°3能拼好分析数据引导学生分析收集的数据,寻找其中的规律.n = 360°×6 = 360°360°能被60°整除n = 490°×4 = 360°360°能被90°整除n = 5108°×3 <360° 360°不能被108°整除108°×4 >360°n = 6120°×3 =360°360°能被120°整除实验思考让学生思考为什么有的正多边形能进行镶嵌,而有的正多边形不能?用一种正多边形镶嵌需要满足什么条件呢?得出结论学生根据自己实验的结果,不难得出结论:正三角形、正四边形、正六边形能够镶嵌,正五边形不能镶嵌.用一种正多边形镶嵌,则这个正多边形的内角度数能整除360°.延伸拓展问:如果用一种多边形进行镶嵌时不采用正多边形,而改为任意多边形,有没有这样的多边形?有,请指出,并说明理由.结论:有,分别是三角形、四边形,但三角形、四边形各自应形状、大小完全相同.理由:三角形、四边形的内角和均能整除360°.6、质疑思考:用两种正多边形镶嵌需满足什么条件?猜想对于正三角形、正四边形、正五边形、正六边形、正八边形,哪两种正多边形能进行镶嵌?操作学生拿出课前准备好的这些正多边形,仍然以小组为单位进行拼图,看哪些能用来搭配镶嵌成一个平面.(边做边记录)结果(a) 3个正三角形与2个正四边形 60°×3+90°×2=360°(b)2个正三角形与2个正六边形 60°×2+120°×2=360°(c) 4个正三角形与1个正六边形 60°×4+120°×1=360°(d)1个正四边形与2个正八边形 90°×1+135°×2=360°……结论一般地,多边形能镶嵌成平面图案需要满足的条件:拼接在同一个点的各个角的和恰好等于360°(周角);相邻的多边形有公共边.延伸用三种或多种多边形能否进行镶嵌,若能,又需满足什么条件?7、 应用应用并设计正多边形镶嵌的平面图案(若设计有困难,就欣赏已设计好的平面图案)8、布置作业:小结:请学生谈谈本节课的收获和体会.作业:(1)作业本(1) ; (2)设计一幅正多边形镶嵌的平面图案.
教后随笔
教 师 备 课 笔 记
上课日期 月 日 星期
课题 第六章复习(二)----梯形 课型 新授
教学目标 1、通过复习让学生进一步巩固等腰梯形的概念和性质定理、等腰梯形的判定定理。2.在简单的操作活动中发展学生的说理意识、主动探究的习惯,初步体会平移、轴对称的有关知识在研究等腰梯形性质中的运用形问题来解决的化归思想。3、熟练掌握梯形中常见的辅助线的作法。
重点和难点 重点: 梯形的基本知识巩固难点:有关梯形问题,常常用添加辅助线的方法把梯形转化成特殊四边形与三角形的问题来解决.如:作高、平移一腰、平移对角线、延长两腰交于一点、过一腰中点作另一腰的平行线等.
教具准备 多媒体课件,三角板
师 生 活 动 过 程
一、知识回顾通过课本知识小结填空回顾梯形基本知识,完成知识结构图一组对边平行 两腰相等(定义)四边形 梯形 等腰梯形 另一组对边不平行 同一底上两底角相等、两对角线相等 (两种判定方法)二、典型例题分析1、梯形的运用例1 如图,在梯形ABCD中,已知AB∥CD,点E为BC的中点, 设△DEA的面积为,梯形ABCD的面积为,则与的关系为_______.分析:由E点为BC的中点,故可联想延长DE与AB的延长线相交,将梯形的面积转化成三角形的面积.答案:.点评:将四边形转化成三角形是寻求解题思路,探求解题方法的重要途径, 注意适当地作出辅助线,学会转化的数学思想.2.等腰梯形的有关计算例2 已知:如图,等腰梯形ABCD中,AD∥BC,AD=3,AB=4, BC=7.求∠B的度数.解:如过A点作AE∥CD,有 □AECD,则△ABE为等边三角形. 答案:∠B=60°.点评:在梯形中常通过作腰的平行线,构造平行四边形、三角形, 从而把分散的条件集中到三角形中去,从而为证题创造必要的条件.3. 梯形知识的综合运用例3 如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.求: BE的长分析:本题运用轴对称及等腰梯形的性质可解决. 解:(1)由题意得△BEF≌△DFE,∴DE=BE,∵在△BDE中,DE=BE,∠DBE=45°,∴∠BDE=∠DBE=45°,∴∠DEB=90°,∴DE⊥BC.∴EC=(BC-AD)= (8-2)=3.∴BE=5.点评:本题是一道综合题目,它把梯形、全等、三角函数等知识综合在一起,考查了综合运用知识的能力。4、思考题:如图,等腰梯形ABCD中,AD∥BC,M、N分别为AD、BC的中点,E、F分别是BM、CM的中点.(1)求证:四边形MENF是菱形;(2)若MENF是正方形,那么梯形的高与底边BC有何关系 三、课堂练习:P158 12 13 14 15 四、作业:课本P159 16--21
教后随笔
㈠从已知看!已知什么
扶梯AB的坡比为1:0.8,且AE= eq \f(3,2)
能得什么
可求得BE和AB
㈢已知滑梯CD的坡比为1:1.6有何用
㈡从所求看!求什么
求AB+BC+CD
缺什么
缺CD,BC= eq \f(1,2)CD.怎样求CD
图㈠
E1
E2
E3
F1
F2
F3
G1
G2
G3
图㈡
C
A
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
教 师 备 课 笔 记
上课日期 月 日 星期
课题 1.3 二次根式的运算(3) 课型 新授
教学目标 熟练地运用二次根式的性质化简二次根式;会运用二次根式解决简单的实际问题;进一步体验二次根式及其运算的实际意义和应用价值。
重点和难点 重点:本节教学的重点是二次根式及其运算的实际应用.难点:课本上的例7涉及多方面的知识和综合运用,思路比较复杂,是本节教学的难点
教具准备 三角板、多媒体课件
师 生 活 动 过 程
一、创设情境,引入课题二次根式的知识在实际生活中有广泛的用途.如图,我们规定斜坡的铅直高h与水平长度l的比叫做坡比(或坡度),即:坡比 i= 已知斜坡的坡比为3:4,且其高CE=2dm,宽AB=1dm.一只蚂蚁从A点爬到C点,最短路程多少 说明:设计本题有以下目的:⑴介绍预备知识“坡比”;⑵激发学生的兴趣;⑶会用二次根式表示未知量.在Rt△BCE中,BC的长宜直接表示为:BC=;⑷建议用多媒体播放此题目和图片,教师引导学生分析,解答过程宜板书而弃PowerPoint.以下例题同.〖初步体验〗(课本17页课内练习1)二、应用举例〖例1〗(课本15页例6)如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=,BC=CD,一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他经过了多少路程(结果要求先化简,再取近似值,精确到0.01米) 分析:说明:以上的分析过程显示了求解问题的格式化的程序,学生必须养成这样的思维习惯.〖练习一〗(课本18页A组3)〖例2〗(课本16页例7)如图㈠是一张等腰直角三角形彩色纸,AC=BC=40 cm.将斜边上的高CD四等分,然后截出3张宽度相等的长方形纸条.
⑴分别求出3张长方形纸条的长度;
⑵若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图㈡,正方形美术作品的面积最大不能超过多少cm2 分析:⑴①如图㈠,从已知能得什么 在Rt△ABC中,CD⊥,AC=BC=40,易求得AB和CD长(让学生求),则CE3 =E3F3 =F3G3 =G3D = CD,纸条的宽度可求.②怎样求纸条的长度 纸条的总长度=E1E2+F1F2+G1G2 ,如怎样求E1E2(让学生想一想) E1E2 =2CE3.,F1F2和G1G2 呢 同理,F1F2=2CF3 ,G1G2=2CG3 .⑵如图㈡,由⑴得纸条的总长度为60,它被四等分,每条长AC=15,它们所围成的正方形的边长AB多少 AB=AC–BC=10 .〖练习二〗(课本18页B组4)三、小结:谈一谈:本节课你有什么收获?运用二次根式解决简单的实际问题时应注意的的问题四、布置作业1: 作业本(2)2:课本P17页:作业题第1、2、3题,第4、5题选做。
教后随笔
教 师 备 课 笔 记
上课日期 月 日 星期
课题 5.1 多边形(3) 课型 新授
教学目标 1、学生通过自主实践与探索,了解正多边形的概念,发现并理解用一种或两种正多边形能够镶嵌的规律.2、通过学生欣赏图片、动手拼、动脑想、相互交流、展示成果等活动,引导学生解决使用一种或两种正多边形镶嵌的问题,让学生理解正多边形镶嵌的原理:用一种或两种正多边形能够镶嵌需满足哪些条件?会运用正多边形进行简单的平面镶嵌设计。3、关注学生的情感体验,让学生在充分感受到数学美的同时,认识到数学来源于生活并应用于生活.
重点和难点 重点:探究用一种或两种正多边形镶嵌的规律.难点:学生通过数学实验操作发现用正多边形能够镶嵌的规律
教具准备 多媒体课件,三角板, 边长均相等的正三角形、正四边形、正五边形、正六边形、正八边形及任意的但大小、形状完全相同的三角形、四边形纸片若干张.
师 生 活 动 过 程
1.图片欣赏①如图,正三角形、正方形、正六边形是我们熟悉的特殊多边形。这些图形中的边与角分别有什么共同的特征? 正三角形 正方形 正六边形 我们把各边相等、各内角也相等的多边形叫做正多边形。边数为五、七、八的正多边形分别是正五边形、正七边形和正八边形。②从镶嵌艺术作品到一些生活墙壁中的、地板铺设图案.2.交流讨论学生直观感受数学美的同时,引导学生思考:这些图案都是由哪些基本的平面图形构成的?(正三角形、正方形、正五边形、正六边形)学生细心观察后发现,图案中的平面图形有的规则,有的不规则;有的用一种多边形拼成,有的用多种多边形拼成,培养学生分类的思想.3.感知概念讨论这些图形拼成一个平面的共同特征,注意到各图形之间没有空隙,也没有重叠.在充分交流的基础上,用自己的语言概括镶嵌的概念(象这种既无缝隙又不重叠的铺法,我们称为平面的镶嵌).教师给予鼓励和评价.4.提出问题提问:如果让你们设计几种地板图案,需要解决什么问题?学生自主探索,分组研究需要探讨的问题,教师做适当引导.把其中可能列举的典型问题设想如下:(1) 怎样铺设可以不留空隙,也不相互重叠?(2) 可以用哪些图形?(3) 用前面所学的正多边形能否拼成一个平面图形?(4) 哪些正多边形可以镶嵌成一个平面,哪些不能? 根据学生提出的以及本节课需要解决的问题,首先引导学生研究最简单的镶嵌问题.5、探索仅用一种多边形镶嵌,哪些正多边形可以镶嵌成一个片面图案.(1)动手实验全班分成九个小组,拿出课前准备好的正三角形、正四边形、正五边形、正六边形,以小组为单位进行比赛,看哪个小组拼得又快又好,并派代表在投影仪上展示他们的成果.收集数据根据刚才的动手实验,引导学生收集数据,观察结果.正n边形每个内角的度数使用正多边形的个数结果n =360°6能拼好n = 490°4能拼好n = 5108°3不能拼好,有缺口4不能拼好,有重叠n = 6120°3能拼好分析数据引导学生分析收集的数据,寻找其中的规律.n = 360°×6 = 360°360°能被60°整除n = 490°×4 = 360°360°能被90°整除n = 5108°×3 <360° 360°不能被108°整除108°×4 >360°n = 6120°×3 =360°360°能被120°整除实验思考让学生思考为什么有的正多边形能进行镶嵌,而有的正多边形不能?用一种正多边形镶嵌需要满足什么条件呢?得出结论学生根据自己实验的结果,不难得出结论:正三角形、正四边形、正六边形能够镶嵌,正五边形不能镶嵌.用一种正多边形镶嵌,则这个正多边形的内角度数能整除360°.延伸拓展问:如果用一种多边形进行镶嵌时不采用正多边形,而改为任意多边形,有没有这样的多边形?有,请指出,并说明理由.结论:有,分别是三角形、四边形,但三角形、四边形各自应形状、大小完全相同.理由:三角形、四边形的内角和均能整除360°.6、质疑思考:用两种正多边形镶嵌需满足什么条件?猜想对于正三角形、正四边形、正五边形、正六边形、正八边形,哪两种正多边形能进行镶嵌?操作学生拿出课前准备好的这些正多边形,仍然以小组为单位进行拼图,看哪些能用来搭配镶嵌成一个平面.(边做边记录)结果(a) 3个正三角形与2个正四边形 60°×3+90°×2=360°(b)2个正三角形与2个正六边形 60°×2+120°×2=360°(c) 4个正三角形与1个正六边形 60°×4+120°×1=360°(d)1个正四边形与2个正八边形 90°×1+135°×2=360°……结论一般地,多边形能镶嵌成平面图案需要满足的条件:拼接在同一个点的各个角的和恰好等于360°(周角);相邻的多边形有公共边.延伸用三种或多种多边形能否进行镶嵌,若能,又需满足什么条件?7、 应用应用并设计正多边形镶嵌的平面图案(若设计有困难,就欣赏已设计好的平面图案)8、布置作业:小结:请学生谈谈本节课的收获和体会.作业:(1)作业本(1) ; (2)设计一幅正多边形镶嵌的平面图案.
教后随笔
教 师 备 课 笔 记
上课日期 月 日 星期
课题 第六章复习(二)----梯形 课型 新授
教学目标 1、通过复习让学生进一步巩固等腰梯形的概念和性质定理、等腰梯形的判定定理。2.在简单的操作活动中发展学生的说理意识、主动探究的习惯,初步体会平移、轴对称的有关知识在研究等腰梯形性质中的运用形问题来解决的化归思想。3、熟练掌握梯形中常见的辅助线的作法。
重点和难点 重点: 梯形的基本知识巩固难点:有关梯形问题,常常用添加辅助线的方法把梯形转化成特殊四边形与三角形的问题来解决.如:作高、平移一腰、平移对角线、延长两腰交于一点、过一腰中点作另一腰的平行线等.
教具准备 多媒体课件,三角板
师 生 活 动 过 程
一、知识回顾通过课本知识小结填空回顾梯形基本知识,完成知识结构图一组对边平行 两腰相等(定义)四边形 梯形 等腰梯形 另一组对边不平行 同一底上两底角相等、两对角线相等 (两种判定方法)二、典型例题分析1、梯形的运用例1 如图,在梯形ABCD中,已知AB∥CD,点E为BC的中点, 设△DEA的面积为,梯形ABCD的面积为,则与的关系为_______.分析:由E点为BC的中点,故可联想延长DE与AB的延长线相交,将梯形的面积转化成三角形的面积.答案:.点评:将四边形转化成三角形是寻求解题思路,探求解题方法的重要途径, 注意适当地作出辅助线,学会转化的数学思想.2.等腰梯形的有关计算例2 已知:如图,等腰梯形ABCD中,AD∥BC,AD=3,AB=4, BC=7.求∠B的度数.解:如过A点作AE∥CD,有 □AECD,则△ABE为等边三角形. 答案:∠B=60°.点评:在梯形中常通过作腰的平行线,构造平行四边形、三角形, 从而把分散的条件集中到三角形中去,从而为证题创造必要的条件.3. 梯形知识的综合运用例3 如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.求: BE的长分析:本题运用轴对称及等腰梯形的性质可解决. 解:(1)由题意得△BEF≌△DFE,∴DE=BE,∵在△BDE中,DE=BE,∠DBE=45°,∴∠BDE=∠DBE=45°,∴∠DEB=90°,∴DE⊥BC.∴EC=(BC-AD)= (8-2)=3.∴BE=5.点评:本题是一道综合题目,它把梯形、全等、三角函数等知识综合在一起,考查了综合运用知识的能力。4、思考题:如图,等腰梯形ABCD中,AD∥BC,M、N分别为AD、BC的中点,E、F分别是BM、CM的中点.(1)求证:四边形MENF是菱形;(2)若MENF是正方形,那么梯形的高与底边BC有何关系 三、课堂练习:P158 12 13 14 15 四、作业:课本P159 16--21
教后随笔
㈠从已知看!已知什么
扶梯AB的坡比为1:0.8,且AE= eq \f(3,2)
能得什么
可求得BE和AB
㈢已知滑梯CD的坡比为1:1.6有何用
㈡从所求看!求什么
求AB+BC+CD
缺什么
缺CD,BC= eq \f(1,2)CD.怎样求CD
图㈠
E1
E2
E3
F1
F2
F3
G1
G2
G3
图㈡
C
A
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
