八年级数学 下册试题 4.4 平行四边形的判定定理同步练习-浙教版(含答案)
文档属性
| 名称 | 八年级数学 下册试题 4.4 平行四边形的判定定理同步练习-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 985.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 21:58:19 | ||
图片预览



文档简介
4.4 平行四边形的判定定理
一、单选题
1.已知四边形ABCD,下列条件能判断它是平行四边形的是( )
A.ABCD,AD=BC B.∠A=∠D,∠B=∠C
C.ABCD,AB=CD D.AB=CD,∠A=∠C
2.将△ABC平移得到△,若,则的度数是( )
A.10° B.80° C.100° D.160°
3.百度百科这样定义凹四边形:把四边形的某边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.关于凹四边形(如图),以下结论:
①;
②若,则;
③若,则;
④存在凹四边形,有.
其中所有正确结论的序号是( )
A.①② B.①②③ C.①②④ D.①③④
4.如图,将绕边的中点O顺时针旋转.嘉淇发现,旋转后的与构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵,”和“∴四边形…”之间作补充,下列补充不正确的是( )
点A,C分别转到了点C,A处, 而点B转到了点D处. ∵, ∴四边形是平行四边形.
A.应补充:且 B.应补充:且
C.应补充:且 D.应补充:且
5.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
6.如图,将 DEBF的对角线EF向两端延长,分别至点A和点C,且使AE=CF,连接AB,BC,AD,CD.求证:四边形ABCD为平行四边形.
以下是证明过程,其顺序已被打乱,
①∴四边形ABCD为平行四边形;
②∵四边形DEBF为平行四边形,∴OD=OB,OE=OF;
③连接BD,交AC于点O;
④又∵AE=CF,∴AE+OE=CF+OF,即OA=OC
正确的证明步骤是( )
A.①②③④ B.③④②① C.③②④① D.④③②①
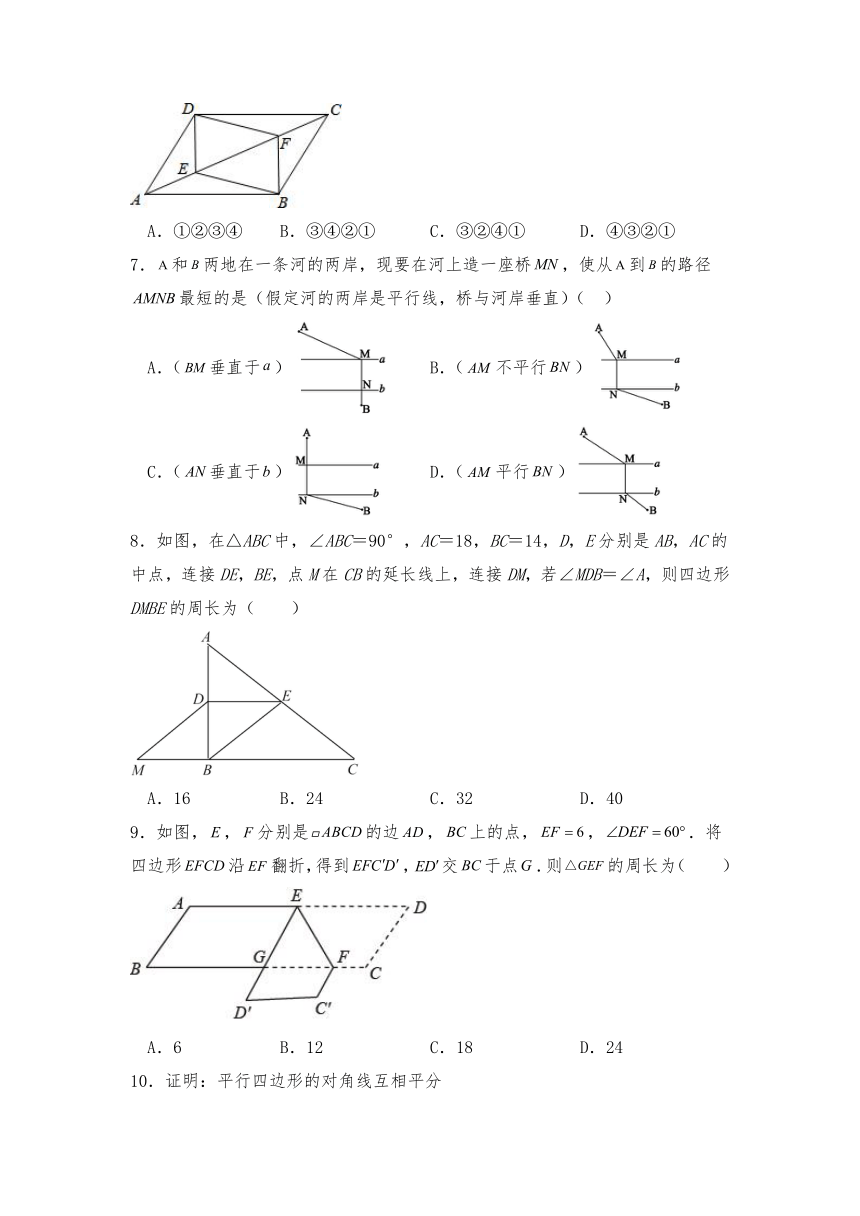
7.和两地在一条河的两岸,现要在河上造一座桥,使从到的路径最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.(垂直于) B.(不平行)
C.(垂直于) D.(平行)
8.如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( )
A.16 B.24 C.32 D.40
9.如图,,分别是的边,上的点,,.将四边形沿翻折,得到,交于点.则的周长为( )
A.6 B.12 C.18 D.24
10.证明:平行四边形的对角线互相平分
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴…
∴∠ABO=∠CDO,∠BAO=∠DCO,
∴△AOB≌△COD,
∴OA=OC,OB=OD
其中,在“四边形ABCD是平行四边形”与“∠ABO=∠CDO,∠BAO=∠DCO”之间应补充的步骤是( )
A.AB=CD,AD=BC B.AD//BC,AD=BC
C.AB//CD,AD//BC D.AB//CD,AB=CD
11.如图,设是边上任意一点,设的面积为,的面积为,的面积为,则( )
A. B. C. D.不能确定
二、填空题
12.如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
13.已知平面上有三个点,点,以点,点点为顶点画平行四边形,则第四个顶点的坐标为____.
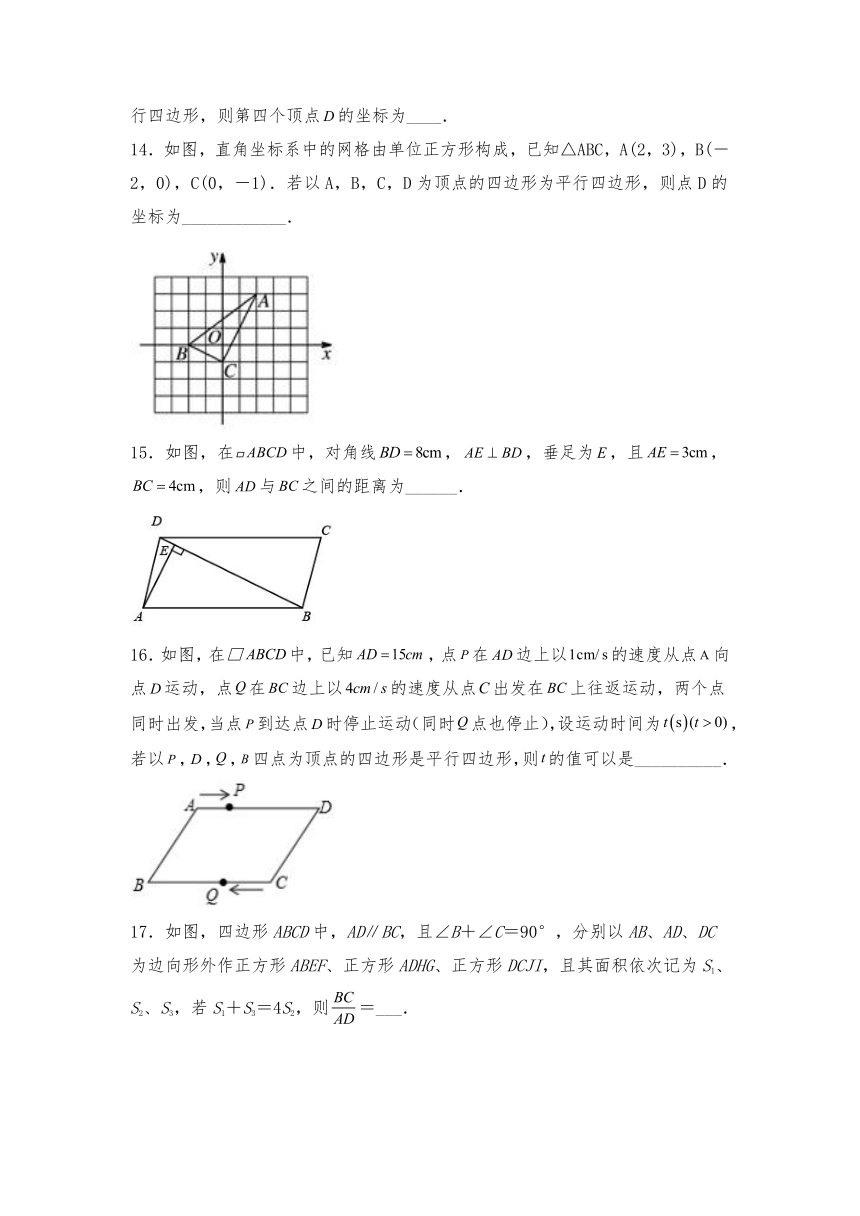
14.如图,直角坐标系中的网格由单位正方形构成,已知△ABC,A(2,3),B(-2,0),C(0,-1).若以A,B,C,D为顶点的四边形为平行四边形,则点D的坐标为____________.
15.如图,在中,对角线,,垂足为,且,,则与之间的距离为______.
16.如图,在□中,已知,点在边上以的速度从点向点运动,点在边上以的速度从点出发在上往返运动,两个点同时出发,当点到达点时停止运动(同时点也停止),设运动时间为,若以,,,四点为顶点的四边形是平行四边形,则的值可以是__________.
17.如图,四边形ABCD中,AD∥BC,且∠B+∠C=90°,分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI,且其面积依次记为S1、S2、S3,若S1+S3=4S2,则=___.
18.如图,在 ABCD中,点E是对角线AC上一点,过点E作AC的垂线,交边AD于点P,交边BC于点Q,连接PC、AQ,若AC=6,PQ=4,则PC+AQ的最小值为________________.
19.如图,己知中,点M是BC的中点,线段AM、BD互相垂直,AM=3,BD=6,则该平行四 边形的面积为____.
20.如图,四边形ABCD中,AB∥CD,AD∥BC,且∠BAD、∠ADC的角平分线AE、DF分别交BC于点E、F.若EF=2,AB=5,则AD的长为_______.
21.如图,在平行四边形ABCD中,,E、F分别在CD和BC的延长线上,,,则______.
22.如图,在△ABC中,AC=3,AB=4,BC=5,且△ABD,△ACF,△BCE都是等边三角形,下列结论中:①∠BAC=90°;②四边形AFED为平行四边形;③四边形AFED面积为10;④∠DEF=30°,正确的是___.(填序号即可)
三、解答题
23.点D是的边上一点,且,点E是的中点,若,求的长.
24.如图,点B是∠MAN的边AM上的定点,点C是边AN上的动点,将△ABC绕点逆时针旋转得到△DBE,且点A的对应点D恰好落在边AB上,连结CE.当BC=AC时,
(1)求证:四边形ABEC是平行四边形;
(2)若AB=15,AD=18,求AC的长.
25.如图,在四边形中,,,,,,点从点出发以的速度向点运动,点从点出发以的速度向点运动,, 两点同时出发,当点到达点时,两点同时停止运动.设运动时间为.
(1)当时,四边形的面积为 .
(2)若以,,,为顶点的四边形是平行四边形,求的值;
(3)当时,若,则当为何值时,是等腰三角形?
26.如图,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB交CD于点E,交BC于点F,作EG∥AB交CB于点G.
(1)求证:△CEF是等腰三角形;
(2)求证:CF=BG;
(3)若F是CG的中点,EF=1,求AB的长.
27.如图是数学教材的部分内容.
(定理证明)
(1)请根据教材内容,结合图①,写出证明过程.
(定理应用)
(2)如图②,四边形中,、、分别为、、的中点,边、延长线交于点,,则的度数是_______.
(3)如图③,矩形中,,,点在边上,且.将线段绕点旋转一定的角度,得到线段,是线段的中点,直接写出旋转过程中线段长的最大值和最小值.
答案
一、单选题
1.C 2.B 3.A 4.C 5.C 6.C 7.D 8.C 9.C 10.D 11.A
二、填空题
12.①④
13.或或
14.(0,4)或(4,2)或(-4,-4)
15..
16.或或
17.3
18.
19.12
20.8
21.8
22.①②④
三、解答题
23.
延长AE至F,使,连接BF、DF、CF,如图所示:
则,
点E是BD的中点,
,
四边形ABFD是平行四边形,
,∠BFD=∠BAC=60°,
,
,
,
,
是等边三角形,
,
,
,
在和中,
,
,
,
,
.
24.
解:(1)∵△ABC绕点B逆时针旋转得到△DBE,
∴AB=BD,BC=BE,∠ABC=∠DBE,
∴∠A=∠BDA,
∵BC=AC,
∴∠A=∠ABC,BE=AC,
∴∠BDA=∠DBE,
∴BE∥AC,
∴四边形ABEC是平行四边形;
(2)如图,过点B作BH⊥AD,垂足为H,
∵BD=BA,BH⊥AD,
∴AH=AD=9,
在Rt△ABH中,由勾股定理得:
BH==12,
设AC=BC=x,则CH=x-9,
在Rt△HCB中,由勾股定理得:
(x-9)2+122=x2,
解得=,
∴AC的长为.
25.
解:(1)∵边形中,,,,,,
点从点出发以的速度向点运动,点从点出发以的速度向点运动,
当时,AQ=4cm,PB=8cm,
∴DQ=16-2=12cm,PC=20-8=12cm,
∴DQ =PC,
∴此时四边形为平行四边形,
四边形的面积为:,
故答案为:;
(2)未到达点时,要使四边形是平行四边形,
则,
,
解得.
四边形是平行四边形时,的值是.
(3)①如图,若,
过点作于点,
则,
,
,
,
,
解得:.
②如图,若,
过作于,
则,
,
在中,
,
,
解得.
当或时,是等腰三角形.
26.
(1)证明:过E作EM∥BC交AB于M,
∵EG∥AB,
∴四边形EMBG是平行四边形,
∴BG=EM,∠B=∠EMD,
∵CD⊥AB,
∴∠ADC=∠ACB=90°,
∴∠1+∠7=90°,∠2+∠3=90°,
∵AE平分∠CAB,
∴∠1=∠2,
∵∠3=∠4,
∴∠4=∠7,
∴CE=CF,
∴△CEF是等腰三角形;
(2)证明:
过E作EM∥BC交AB于M,则四边形EMBG是平行四边形,
∴BG=EM,
∵∠ADC=∠ACB=90°,
∴∠CAD+∠B=90°,∠CAD+∠ACD=90°,
∴∠ACD=∠B=∠EMD,
∵在△CAE和△MAE中
,
∴△CAE≌△MAE(AAS),
∴CE=EM,
∵CE=CF,EM=BG,
∴CF=BG.
(3)∵CD⊥AB,EG∥AB,
∴EG⊥CD,
∴∠CEG=90°,
∵CF=FG,
∴EF=CF=FG,
∵CE=CF,
∴CE=CF=EF=1,
∴△CEF是等边三角形,
∴∠ECF=60°,
∴BC=3,∠B=30°,
∴
∴Rt△ABC中
∴
解得.
27.
(1)证明:延长至,使,连接,
在和中,
,
,
,,
,
,
,
四边形为平行四边形,
,,
,;
(2)∵、、分别为、、的中点,
∴是△DAB的中位线,是△BCD的中位线,
∴,,
∴,,
又∵,
∴,
∴;
(3)解:延长至,使,连接,,
,,
,由勾股定理得,,
当点在线段上时,最小,最小值为,
当点在线段的延长线上时,最大,最大值为,
长的最大值为,最小值为.
一、单选题
1.已知四边形ABCD,下列条件能判断它是平行四边形的是( )
A.ABCD,AD=BC B.∠A=∠D,∠B=∠C
C.ABCD,AB=CD D.AB=CD,∠A=∠C
2.将△ABC平移得到△,若,则的度数是( )
A.10° B.80° C.100° D.160°
3.百度百科这样定义凹四边形:把四边形的某边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.关于凹四边形(如图),以下结论:
①;
②若,则;
③若,则;
④存在凹四边形,有.
其中所有正确结论的序号是( )
A.①② B.①②③ C.①②④ D.①③④
4.如图,将绕边的中点O顺时针旋转.嘉淇发现,旋转后的与构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵,”和“∴四边形…”之间作补充,下列补充不正确的是( )
点A,C分别转到了点C,A处, 而点B转到了点D处. ∵, ∴四边形是平行四边形.
A.应补充:且 B.应补充:且
C.应补充:且 D.应补充:且
5.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
6.如图,将 DEBF的对角线EF向两端延长,分别至点A和点C,且使AE=CF,连接AB,BC,AD,CD.求证:四边形ABCD为平行四边形.
以下是证明过程,其顺序已被打乱,
①∴四边形ABCD为平行四边形;
②∵四边形DEBF为平行四边形,∴OD=OB,OE=OF;
③连接BD,交AC于点O;
④又∵AE=CF,∴AE+OE=CF+OF,即OA=OC
正确的证明步骤是( )
A.①②③④ B.③④②① C.③②④① D.④③②①
7.和两地在一条河的两岸,现要在河上造一座桥,使从到的路径最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.(垂直于) B.(不平行)
C.(垂直于) D.(平行)
8.如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( )
A.16 B.24 C.32 D.40
9.如图,,分别是的边,上的点,,.将四边形沿翻折,得到,交于点.则的周长为( )
A.6 B.12 C.18 D.24
10.证明:平行四边形的对角线互相平分
已知:如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴…
∴∠ABO=∠CDO,∠BAO=∠DCO,
∴△AOB≌△COD,
∴OA=OC,OB=OD
其中,在“四边形ABCD是平行四边形”与“∠ABO=∠CDO,∠BAO=∠DCO”之间应补充的步骤是( )
A.AB=CD,AD=BC B.AD//BC,AD=BC
C.AB//CD,AD//BC D.AB//CD,AB=CD
11.如图,设是边上任意一点,设的面积为,的面积为,的面积为,则( )
A. B. C. D.不能确定
二、填空题
12.如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
13.已知平面上有三个点,点,以点,点点为顶点画平行四边形,则第四个顶点的坐标为____.
14.如图,直角坐标系中的网格由单位正方形构成,已知△ABC,A(2,3),B(-2,0),C(0,-1).若以A,B,C,D为顶点的四边形为平行四边形,则点D的坐标为____________.
15.如图,在中,对角线,,垂足为,且,,则与之间的距离为______.
16.如图,在□中,已知,点在边上以的速度从点向点运动,点在边上以的速度从点出发在上往返运动,两个点同时出发,当点到达点时停止运动(同时点也停止),设运动时间为,若以,,,四点为顶点的四边形是平行四边形,则的值可以是__________.
17.如图,四边形ABCD中,AD∥BC,且∠B+∠C=90°,分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI,且其面积依次记为S1、S2、S3,若S1+S3=4S2,则=___.
18.如图,在 ABCD中,点E是对角线AC上一点,过点E作AC的垂线,交边AD于点P,交边BC于点Q,连接PC、AQ,若AC=6,PQ=4,则PC+AQ的最小值为________________.
19.如图,己知中,点M是BC的中点,线段AM、BD互相垂直,AM=3,BD=6,则该平行四 边形的面积为____.
20.如图,四边形ABCD中,AB∥CD,AD∥BC,且∠BAD、∠ADC的角平分线AE、DF分别交BC于点E、F.若EF=2,AB=5,则AD的长为_______.
21.如图,在平行四边形ABCD中,,E、F分别在CD和BC的延长线上,,,则______.
22.如图,在△ABC中,AC=3,AB=4,BC=5,且△ABD,△ACF,△BCE都是等边三角形,下列结论中:①∠BAC=90°;②四边形AFED为平行四边形;③四边形AFED面积为10;④∠DEF=30°,正确的是___.(填序号即可)
三、解答题
23.点D是的边上一点,且,点E是的中点,若,求的长.
24.如图,点B是∠MAN的边AM上的定点,点C是边AN上的动点,将△ABC绕点逆时针旋转得到△DBE,且点A的对应点D恰好落在边AB上,连结CE.当BC=AC时,
(1)求证:四边形ABEC是平行四边形;
(2)若AB=15,AD=18,求AC的长.
25.如图,在四边形中,,,,,,点从点出发以的速度向点运动,点从点出发以的速度向点运动,, 两点同时出发,当点到达点时,两点同时停止运动.设运动时间为.
(1)当时,四边形的面积为 .
(2)若以,,,为顶点的四边形是平行四边形,求的值;
(3)当时,若,则当为何值时,是等腰三角形?
26.如图,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB交CD于点E,交BC于点F,作EG∥AB交CB于点G.
(1)求证:△CEF是等腰三角形;
(2)求证:CF=BG;
(3)若F是CG的中点,EF=1,求AB的长.
27.如图是数学教材的部分内容.
(定理证明)
(1)请根据教材内容,结合图①,写出证明过程.
(定理应用)
(2)如图②,四边形中,、、分别为、、的中点,边、延长线交于点,,则的度数是_______.
(3)如图③,矩形中,,,点在边上,且.将线段绕点旋转一定的角度,得到线段,是线段的中点,直接写出旋转过程中线段长的最大值和最小值.
答案
一、单选题
1.C 2.B 3.A 4.C 5.C 6.C 7.D 8.C 9.C 10.D 11.A
二、填空题
12.①④
13.或或
14.(0,4)或(4,2)或(-4,-4)
15..
16.或或
17.3
18.
19.12
20.8
21.8
22.①②④
三、解答题
23.
延长AE至F,使,连接BF、DF、CF,如图所示:
则,
点E是BD的中点,
,
四边形ABFD是平行四边形,
,∠BFD=∠BAC=60°,
,
,
,
,
是等边三角形,
,
,
,
在和中,
,
,
,
,
.
24.
解:(1)∵△ABC绕点B逆时针旋转得到△DBE,
∴AB=BD,BC=BE,∠ABC=∠DBE,
∴∠A=∠BDA,
∵BC=AC,
∴∠A=∠ABC,BE=AC,
∴∠BDA=∠DBE,
∴BE∥AC,
∴四边形ABEC是平行四边形;
(2)如图,过点B作BH⊥AD,垂足为H,
∵BD=BA,BH⊥AD,
∴AH=AD=9,
在Rt△ABH中,由勾股定理得:
BH==12,
设AC=BC=x,则CH=x-9,
在Rt△HCB中,由勾股定理得:
(x-9)2+122=x2,
解得=,
∴AC的长为.
25.
解:(1)∵边形中,,,,,,
点从点出发以的速度向点运动,点从点出发以的速度向点运动,
当时,AQ=4cm,PB=8cm,
∴DQ=16-2=12cm,PC=20-8=12cm,
∴DQ =PC,
∴此时四边形为平行四边形,
四边形的面积为:,
故答案为:;
(2)未到达点时,要使四边形是平行四边形,
则,
,
解得.
四边形是平行四边形时,的值是.
(3)①如图,若,
过点作于点,
则,
,
,
,
,
解得:.
②如图,若,
过作于,
则,
,
在中,
,
,
解得.
当或时,是等腰三角形.
26.
(1)证明:过E作EM∥BC交AB于M,
∵EG∥AB,
∴四边形EMBG是平行四边形,
∴BG=EM,∠B=∠EMD,
∵CD⊥AB,
∴∠ADC=∠ACB=90°,
∴∠1+∠7=90°,∠2+∠3=90°,
∵AE平分∠CAB,
∴∠1=∠2,
∵∠3=∠4,
∴∠4=∠7,
∴CE=CF,
∴△CEF是等腰三角形;
(2)证明:
过E作EM∥BC交AB于M,则四边形EMBG是平行四边形,
∴BG=EM,
∵∠ADC=∠ACB=90°,
∴∠CAD+∠B=90°,∠CAD+∠ACD=90°,
∴∠ACD=∠B=∠EMD,
∵在△CAE和△MAE中
,
∴△CAE≌△MAE(AAS),
∴CE=EM,
∵CE=CF,EM=BG,
∴CF=BG.
(3)∵CD⊥AB,EG∥AB,
∴EG⊥CD,
∴∠CEG=90°,
∵CF=FG,
∴EF=CF=FG,
∵CE=CF,
∴CE=CF=EF=1,
∴△CEF是等边三角形,
∴∠ECF=60°,
∴BC=3,∠B=30°,
∴
∴Rt△ABC中
∴
解得.
27.
(1)证明:延长至,使,连接,
在和中,
,
,
,,
,
,
,
四边形为平行四边形,
,,
,;
(2)∵、、分别为、、的中点,
∴是△DAB的中位线,是△BCD的中位线,
∴,,
∴,,
又∵,
∴,
∴;
(3)解:延长至,使,连接,,
,,
,由勾股定理得,,
当点在线段上时,最小,最小值为,
当点在线段的延长线上时,最大,最大值为,
长的最大值为,最小值为.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
