浙教版八年级数学下册第3章《数据分析初步》全章复习与巩固-浙教版(含答案)
文档属性
| 名称 | 浙教版八年级数学下册第3章《数据分析初步》全章复习与巩固-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 134.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 22:09:27 | ||
图片预览

文档简介
《数据分析初步》全章复习与巩固
一、单选题
1.7名学生的平均成绩是,如果另外3名学生每人得92分,那么整个组的平均成绩是( )
A. B. C. D.
2.某同学使用计算器求30个数据的平均数时,错将其中的一个数据406输入为46,那么由此求出的平均数与实际平均数的差是( )
A. B.9 C. D.12
3.数学老师计算同学们一学期的总评成绩时,将平时、期中和期末的成绩按2:3:5计算,若小红平时、期中和期末的成绩分别是90分、80分、96分,则小红一学期的数学总评成绩是( )
A.90分 B.91分 C.92分 D.93分
4.某次演讲比赛四名选手的成绩统计如下表(单位:分)
项目 成绩
小李 小张 小王 小周
评委 90 94 85 92
观众 95 88 94 94
将评委、观众按的比例进行打分,成绩最高的是( )
A.小李 B.小张 C.小王 D.小周
5.某种植户为了考察所种植的大蒜的长势,从大蒜田中随机抽取7株大蒜苗,测得苗高(单位:cm)分别是:13,14,13,15,16,13,15.则这组数据的众数和中位数分别是( )
A.14,15 B.13,13 C.13,14 D.14,14
6.某中学运动会上,有名运动员参加了米半决赛,按成绩取前8名进入决赛,小亮知道了自己的成绩,也知道名选手的成绩各不相同,要判断自己能否进入决赛,还要了解全部成绩的( )
A.平均数 B.众数 C.中位数 D.方差
7.一组数据2,4,x,6,8的众数为2,则这组数据的中位数为 ( )
A.2 B.4 C.6 D.8
8.在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法正确的是( )
A.方差是3.6 B.众数是10 C.中位数是3 D.平均数是6
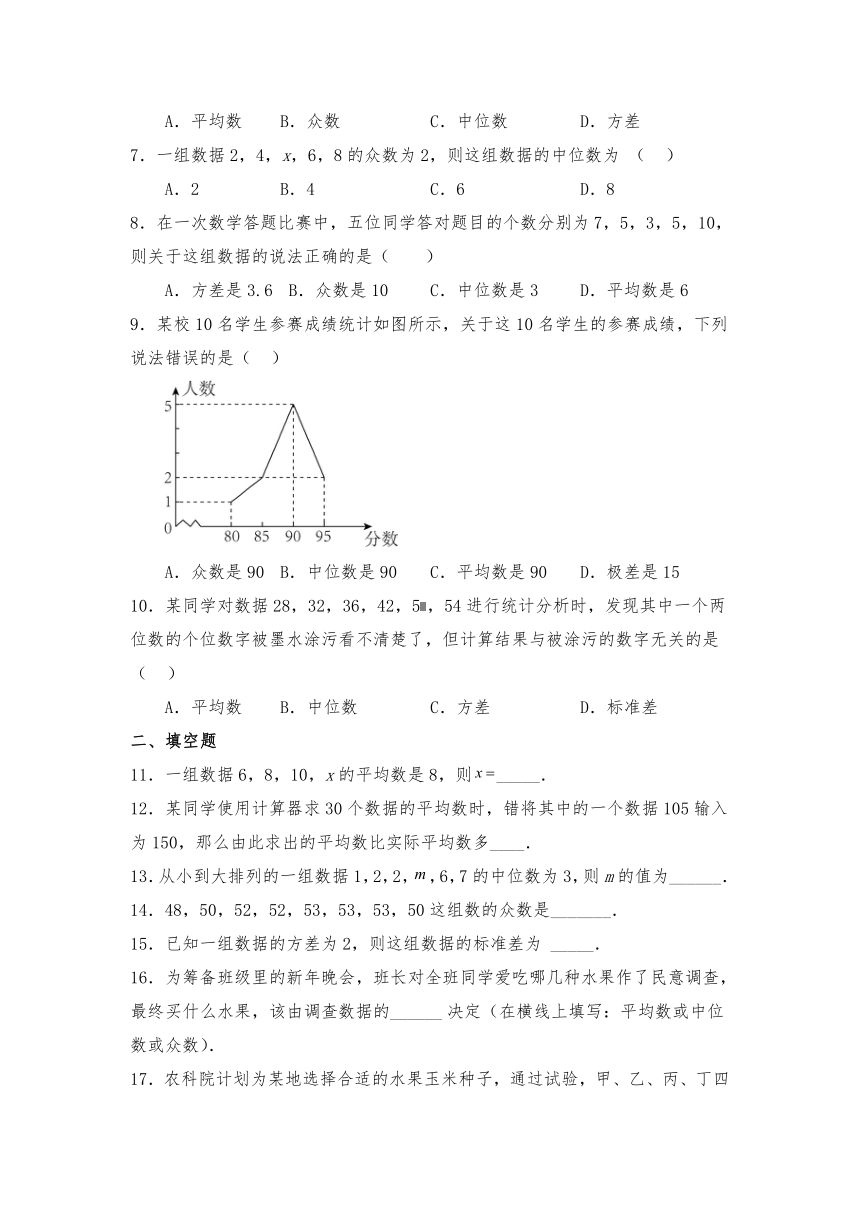
9.某校10名学生参赛成绩统计如图所示,关于这10名学生的参赛成绩,下列说法错误的是( )
A.众数是90 B.中位数是90 C.平均数是90 D.极差是15
10.某同学对数据28,32,36,42,5,54进行统计分析时,发现其中一个两位数的个位数字被墨水涂污看不清楚了,但计算结果与被涂污的数字无关的是( )
A.平均数 B.中位数 C.方差 D.标准差
二、填空题
11.一组数据6,8,10,x的平均数是8,则_____.
12.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为150,那么由此求出的平均数比实际平均数多____.
13.从小到大排列的一组数据1,2,2,,6,7的中位数为3,则m的值为______.
14.48,50,52,52,53,53,53,50这组数的众数是_______.
15.已知一组数据的方差为2,则这组数据的标准差为 _____.
16.为筹备班级里的新年晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果,该由调查数据的______ 决定(在横线上填写:平均数或中位数或众数).
17.农科院计划为某地选择合适的水果玉米种子,通过试验,甲、乙、丙、丁四种水果玉米种子每亩平均产量都是1500千克,方差分别为,,,,这四种水果玉米种子中产量最稳定的是___种水果玉米种子.
18.张明随机抽查了学校七年级63名学生的身高(单位:cm),他准备绘制频数分布直方图,这些数据中最大值是185,最小值是147,若以4为组距(每组两个端点之间的距离叫做组距),则这些数据可分成____组.
三、解答题
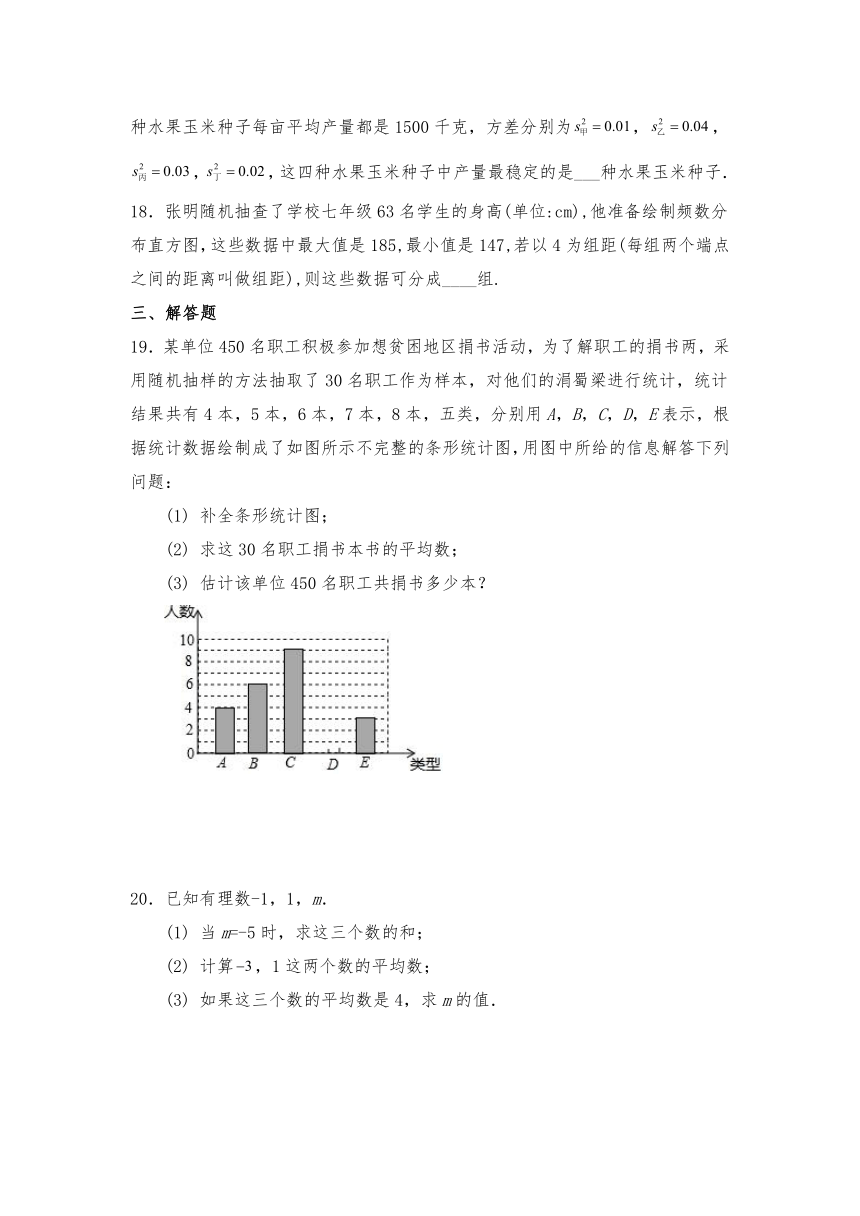
19.某单位450名职工积极参加想贫困地区捐书活动,为了解职工的捐书两,采用随机抽样的方法抽取了30名职工作为样本,对他们的涓蜀梁进行统计,统计结果共有4本,5本,6本,7本,8本,五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示不完整的条形统计图,用图中所给的信息解答下列问题:
(1) 补全条形统计图;
(2) 求这30名职工捐书本书的平均数;
(3) 估计该单位450名职工共捐书多少本?
20.已知有理数-1,1,m.
(1) 当m=-5时,求这三个数的和;
(2) 计算,1这两个数的平均数;
(3) 如果这三个数的平均数是4,求m的值.
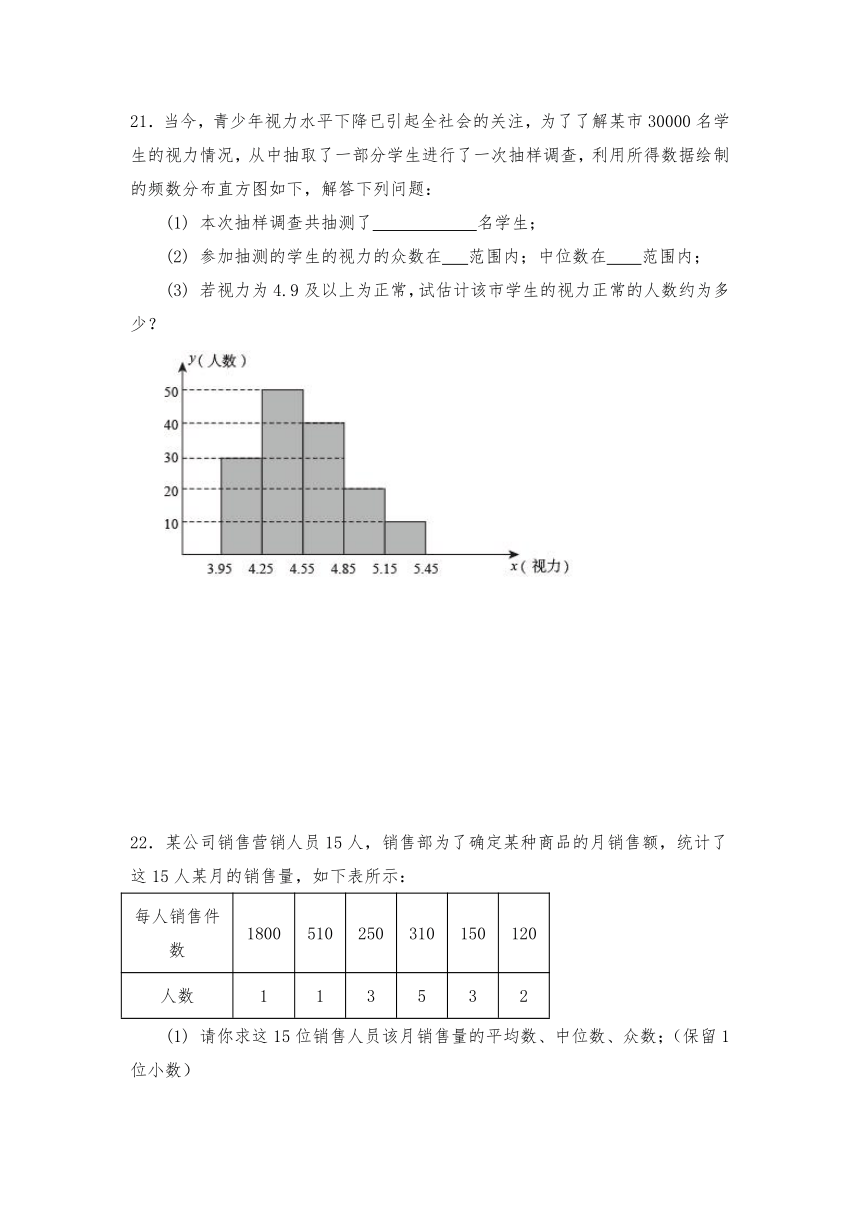
21.当今,青少年视力水平下降已引起全社会的关注,为了了解某市30000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如下,解答下列问题:
(1) 本次抽样调查共抽测了 名学生;
(2) 参加抽测的学生的视力的众数在 范围内;中位数在 范围内;
(3) 若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?
22.某公司销售营销人员15人,销售部为了确定某种商品的月销售额,统计了这15人某月的销售量,如下表所示:
每人销售件数 1800 510 250 310 150 120
人数 1 1 3 5 3 2
请你求这15位销售人员该月销售量的平均数、中位数、众数;(保留1位小数)
假设销售部经理把每位销售员的月销售额定为320件,你认为是否合理?为什么?
23.为了发展体育运动,培养学生的综合能力,某学校成立了足球队、篮球队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如下表:
射击次序(次) 一 二 三 四 五 六 七 八 九 十
甲的成绩(环) 8 9 7 9 8 6 7 a 10 8
乙的成绩(环) 6 7 9 7 9 10 8 7 7 10
经计算甲和乙的平均成绩都是8环,请求出表中的a= ;
甲射击成绩的中位数和乙射击成绩的众数各是多少?
若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
24.本学期某校举行了有关垃圾分类知识测试活动,并从该校七年级和八年级中各随机抽取40名学生的测试成绩,整理如下:小明将样本中的成绩进行了数据处理,如表为数据处理的一部分,根据图表,解答问题:
年级 平均数 众数 中位数 方差
七年级 7.5 7 7 2.8
八年级 a 8 b 2.35
(1)填空:表中的a= ,b= ;
(2)你认为 年级的成绩更加稳定,理由是 ;
(3)若规定6分及6分以上为合格,该校八年级共1200名学生参加了此次测试活动,估计参如此次测试活动成绩合格的学生人数是多少?
答案
一、单选题
1.B 2.A 3.A 4.D 5.C 6.C 7.B 8.D 9.C 10.B
二、填空题
11.8
12.1.5
13.4
14.53
15.
16.众数
17.甲
18.10
三、解答题
19.解:(1)捐D类书的有30﹣4﹣6﹣9﹣3=8(人),
补全的条形统计图如下图所示:
(2)(4×4+5×6+6×9+7×8+8×3)=6(本),
答:这30名职工捐书本数的平均数为6本.
(3)450×6=2700(本),
答:估计该单位450名职工共捐书2700本.
20.
(1)解:m=-5,则三个数为-1,1,-5,
∴这三个数的和为-1+1+(-5)= -5;
(2)解:-3,1的平均数为;
(3)解:根据题意得:-1+1+m=4×3,
∴m=12.
21.(1)解:由图表可得出:30+50+40+20+10=150(名);
故答案为:150;
(2)解:∵4.25~4.55范围内的数据最多,
∴参加抽测的学生的视力的众数在4.25~4.55范围内;
∵150个数据最中间是:第75和76个数据,
∴中位数是第75和76个数据的平均数,
而第75和76个数据在4.25~4.55范围内,
∴中位数在4.25~4.55范围内;
故答案为:4.25~4.55,4.25~4.55;
(3)解:∵视力为4.9及以上为正常,样本中有20+10=30(人),
∴(人),
答:该市学生的视力正常的人数约为6000人.
22.
(1)解:平均数=,
由表格可知,按顺序排列后第7的销售数量为250,
∴中位数为:250,
又∵这组数据中出现次数最多的是310,
∴众数为:310.
(2)不合理,
理由是:多数人没有达到这个额度.
23.(1)解:(1)∵甲的平均成绩是8环,
;
解得:a=8,
(2)甲成绩排序后最中间的两个数据为8和8,
所以甲成绩的中位数是(8+8)=8;
乙成绩中出现次数最多的为7,故乙成绩的众数是7,
(3)乙成绩的方差为:
[(7-8)2×4+(9-8)2×2+(10-8)2×2+(6-8)2+(8-8)2]=1.8,
∴1.2<1.8
∵甲和乙的平均成绩都是8环,而甲成绩的方差小于乙成绩的方差,
∴甲的成绩更为稳定.
24.
(1)解:由表可知,
八年级成绩的平均数a==7.5,
所以a=7.5;
八年级成绩最中间的2个数分别为7、8,
所以其中位数b==7.5,
故答案为:7.5;8
(2)解:八年级的成绩更加稳定,理由是八年级成绩的方差小于七年级,
故答案为:八,八年级成绩的方差小于七年级;
(3)解:估计参如此次测试活动成绩合格的学生人数是1200×=1080(人).
一、单选题
1.7名学生的平均成绩是,如果另外3名学生每人得92分,那么整个组的平均成绩是( )
A. B. C. D.
2.某同学使用计算器求30个数据的平均数时,错将其中的一个数据406输入为46,那么由此求出的平均数与实际平均数的差是( )
A. B.9 C. D.12
3.数学老师计算同学们一学期的总评成绩时,将平时、期中和期末的成绩按2:3:5计算,若小红平时、期中和期末的成绩分别是90分、80分、96分,则小红一学期的数学总评成绩是( )
A.90分 B.91分 C.92分 D.93分
4.某次演讲比赛四名选手的成绩统计如下表(单位:分)
项目 成绩
小李 小张 小王 小周
评委 90 94 85 92
观众 95 88 94 94
将评委、观众按的比例进行打分,成绩最高的是( )
A.小李 B.小张 C.小王 D.小周
5.某种植户为了考察所种植的大蒜的长势,从大蒜田中随机抽取7株大蒜苗,测得苗高(单位:cm)分别是:13,14,13,15,16,13,15.则这组数据的众数和中位数分别是( )
A.14,15 B.13,13 C.13,14 D.14,14
6.某中学运动会上,有名运动员参加了米半决赛,按成绩取前8名进入决赛,小亮知道了自己的成绩,也知道名选手的成绩各不相同,要判断自己能否进入决赛,还要了解全部成绩的( )
A.平均数 B.众数 C.中位数 D.方差
7.一组数据2,4,x,6,8的众数为2,则这组数据的中位数为 ( )
A.2 B.4 C.6 D.8
8.在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法正确的是( )
A.方差是3.6 B.众数是10 C.中位数是3 D.平均数是6
9.某校10名学生参赛成绩统计如图所示,关于这10名学生的参赛成绩,下列说法错误的是( )
A.众数是90 B.中位数是90 C.平均数是90 D.极差是15
10.某同学对数据28,32,36,42,5,54进行统计分析时,发现其中一个两位数的个位数字被墨水涂污看不清楚了,但计算结果与被涂污的数字无关的是( )
A.平均数 B.中位数 C.方差 D.标准差
二、填空题
11.一组数据6,8,10,x的平均数是8,则_____.
12.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为150,那么由此求出的平均数比实际平均数多____.
13.从小到大排列的一组数据1,2,2,,6,7的中位数为3,则m的值为______.
14.48,50,52,52,53,53,53,50这组数的众数是_______.
15.已知一组数据的方差为2,则这组数据的标准差为 _____.
16.为筹备班级里的新年晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果,该由调查数据的______ 决定(在横线上填写:平均数或中位数或众数).
17.农科院计划为某地选择合适的水果玉米种子,通过试验,甲、乙、丙、丁四种水果玉米种子每亩平均产量都是1500千克,方差分别为,,,,这四种水果玉米种子中产量最稳定的是___种水果玉米种子.
18.张明随机抽查了学校七年级63名学生的身高(单位:cm),他准备绘制频数分布直方图,这些数据中最大值是185,最小值是147,若以4为组距(每组两个端点之间的距离叫做组距),则这些数据可分成____组.
三、解答题
19.某单位450名职工积极参加想贫困地区捐书活动,为了解职工的捐书两,采用随机抽样的方法抽取了30名职工作为样本,对他们的涓蜀梁进行统计,统计结果共有4本,5本,6本,7本,8本,五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示不完整的条形统计图,用图中所给的信息解答下列问题:
(1) 补全条形统计图;
(2) 求这30名职工捐书本书的平均数;
(3) 估计该单位450名职工共捐书多少本?
20.已知有理数-1,1,m.
(1) 当m=-5时,求这三个数的和;
(2) 计算,1这两个数的平均数;
(3) 如果这三个数的平均数是4,求m的值.
21.当今,青少年视力水平下降已引起全社会的关注,为了了解某市30000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如下,解答下列问题:
(1) 本次抽样调查共抽测了 名学生;
(2) 参加抽测的学生的视力的众数在 范围内;中位数在 范围内;
(3) 若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?
22.某公司销售营销人员15人,销售部为了确定某种商品的月销售额,统计了这15人某月的销售量,如下表所示:
每人销售件数 1800 510 250 310 150 120
人数 1 1 3 5 3 2
请你求这15位销售人员该月销售量的平均数、中位数、众数;(保留1位小数)
假设销售部经理把每位销售员的月销售额定为320件,你认为是否合理?为什么?
23.为了发展体育运动,培养学生的综合能力,某学校成立了足球队、篮球队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如下表:
射击次序(次) 一 二 三 四 五 六 七 八 九 十
甲的成绩(环) 8 9 7 9 8 6 7 a 10 8
乙的成绩(环) 6 7 9 7 9 10 8 7 7 10
经计算甲和乙的平均成绩都是8环,请求出表中的a= ;
甲射击成绩的中位数和乙射击成绩的众数各是多少?
若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?
24.本学期某校举行了有关垃圾分类知识测试活动,并从该校七年级和八年级中各随机抽取40名学生的测试成绩,整理如下:小明将样本中的成绩进行了数据处理,如表为数据处理的一部分,根据图表,解答问题:
年级 平均数 众数 中位数 方差
七年级 7.5 7 7 2.8
八年级 a 8 b 2.35
(1)填空:表中的a= ,b= ;
(2)你认为 年级的成绩更加稳定,理由是 ;
(3)若规定6分及6分以上为合格,该校八年级共1200名学生参加了此次测试活动,估计参如此次测试活动成绩合格的学生人数是多少?
答案
一、单选题
1.B 2.A 3.A 4.D 5.C 6.C 7.B 8.D 9.C 10.B
二、填空题
11.8
12.1.5
13.4
14.53
15.
16.众数
17.甲
18.10
三、解答题
19.解:(1)捐D类书的有30﹣4﹣6﹣9﹣3=8(人),
补全的条形统计图如下图所示:
(2)(4×4+5×6+6×9+7×8+8×3)=6(本),
答:这30名职工捐书本数的平均数为6本.
(3)450×6=2700(本),
答:估计该单位450名职工共捐书2700本.
20.
(1)解:m=-5,则三个数为-1,1,-5,
∴这三个数的和为-1+1+(-5)= -5;
(2)解:-3,1的平均数为;
(3)解:根据题意得:-1+1+m=4×3,
∴m=12.
21.(1)解:由图表可得出:30+50+40+20+10=150(名);
故答案为:150;
(2)解:∵4.25~4.55范围内的数据最多,
∴参加抽测的学生的视力的众数在4.25~4.55范围内;
∵150个数据最中间是:第75和76个数据,
∴中位数是第75和76个数据的平均数,
而第75和76个数据在4.25~4.55范围内,
∴中位数在4.25~4.55范围内;
故答案为:4.25~4.55,4.25~4.55;
(3)解:∵视力为4.9及以上为正常,样本中有20+10=30(人),
∴(人),
答:该市学生的视力正常的人数约为6000人.
22.
(1)解:平均数=,
由表格可知,按顺序排列后第7的销售数量为250,
∴中位数为:250,
又∵这组数据中出现次数最多的是310,
∴众数为:310.
(2)不合理,
理由是:多数人没有达到这个额度.
23.(1)解:(1)∵甲的平均成绩是8环,
;
解得:a=8,
(2)甲成绩排序后最中间的两个数据为8和8,
所以甲成绩的中位数是(8+8)=8;
乙成绩中出现次数最多的为7,故乙成绩的众数是7,
(3)乙成绩的方差为:
[(7-8)2×4+(9-8)2×2+(10-8)2×2+(6-8)2+(8-8)2]=1.8,
∴1.2<1.8
∵甲和乙的平均成绩都是8环,而甲成绩的方差小于乙成绩的方差,
∴甲的成绩更为稳定.
24.
(1)解:由表可知,
八年级成绩的平均数a==7.5,
所以a=7.5;
八年级成绩最中间的2个数分别为7、8,
所以其中位数b==7.5,
故答案为:7.5;8
(2)解:八年级的成绩更加稳定,理由是八年级成绩的方差小于七年级,
故答案为:八,八年级成绩的方差小于七年级;
(3)解:估计参如此次测试活动成绩合格的学生人数是1200×=1080(人).
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
