八年级数学 下册试题 《特殊平行四边形》本章复习-浙教版(含答案)
文档属性
| 名称 | 八年级数学 下册试题 《特殊平行四边形》本章复习-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 22:44:52 | ||
图片预览


文档简介
《特殊平行四边形》本章复习
一、单选题
1.在一组对边平行的四边形中,增加一个条件,使得这个四边形是菱形,那么增加的条件可以是( )
A.另一组对边相等,对角线相等 B.另一组对边相等,对角线互相垂直
C.另一组对边平行,对角线相等 D.另一组对边平行,对角线相互垂直
2.若菱形的两条对角线长分别为6和8,则它的周长为( )
A.14 B.16 C.20 D.24
3.如图,菱形中,,,于点,则( )
A.24 B.10 C. D.
4.如图,在菱形ABCD中,∠B=60°,E是BC的中点,连接AE,DE,DE与AC交于点G、以DE为边作等边三角形DEF,连接AF交DE于点N,交DC于点M.下列结论:①;②∠EAN=45°;③;④点M为AF的中点.其中结论正确的序号有( )
A.①②③ B.①②④ C.②③④ D.①③④
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,BC=2AB=8,点P是BC上一点,PE⊥AC于点E,PF⊥BD于点F,若m=PE+PF,则m的值为( ).
A. B. C. D.
6.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
7.如图,菱形的对角线相交于点O,点P为边上一动点(不与点A,B重合),于点E,于点F.若,,则的最小值为( )
A. B. C.4 D.
8.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
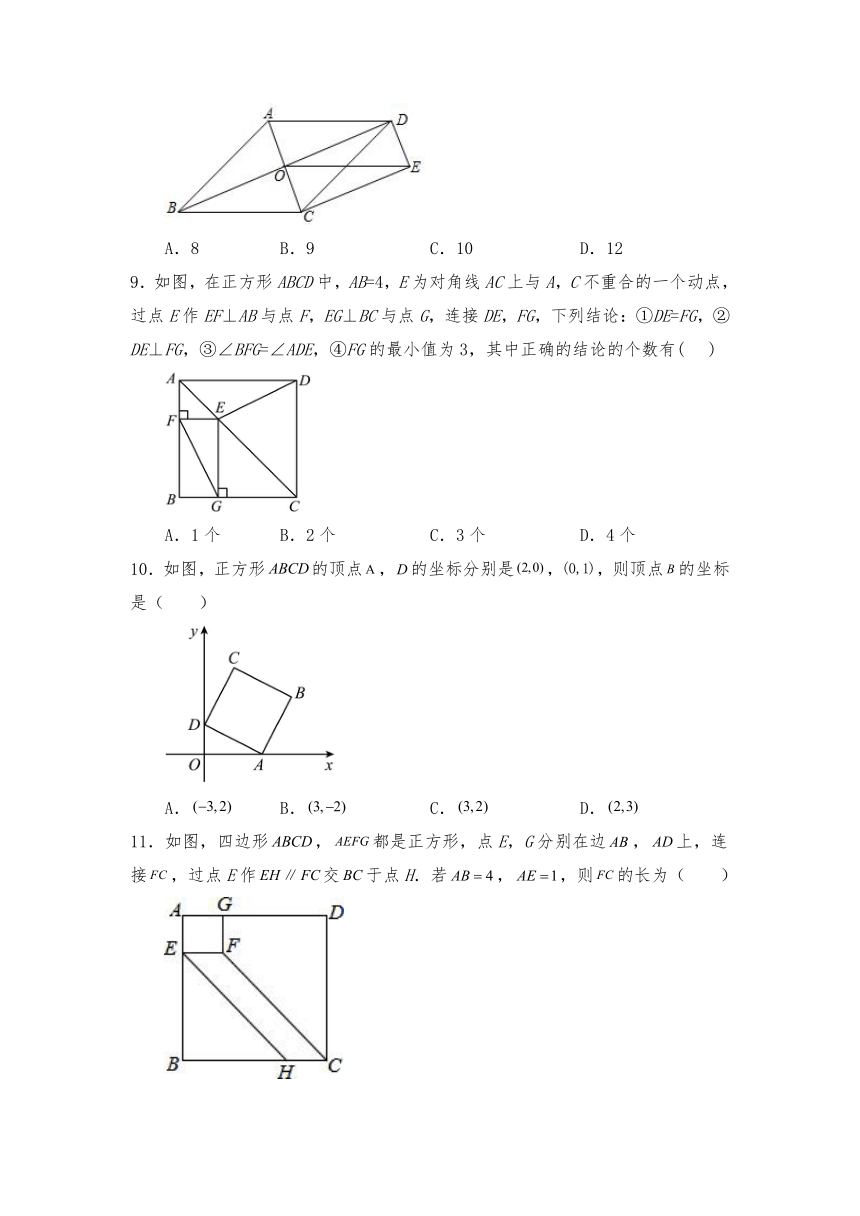
9.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB与点F,EG⊥BC与点G,连接DE,FG,下列结论:①DE=FG,②DE⊥FG,③∠BFG=∠ADE,④FG的最小值为3,其中正确的结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形的顶点,的坐标分别是,,则顶点的坐标是( )
A. B. C. D.
11.如图,四边形,都是正方形,点E,G分别在边,上,连接,过点E作交于点H.若,,则的长为( )
A.1 B.2 C.3 D.
12.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为6的正方形的边在轴上,的中点是坐标原点,固定点,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为( )
A. B. C. D.
二、填空题
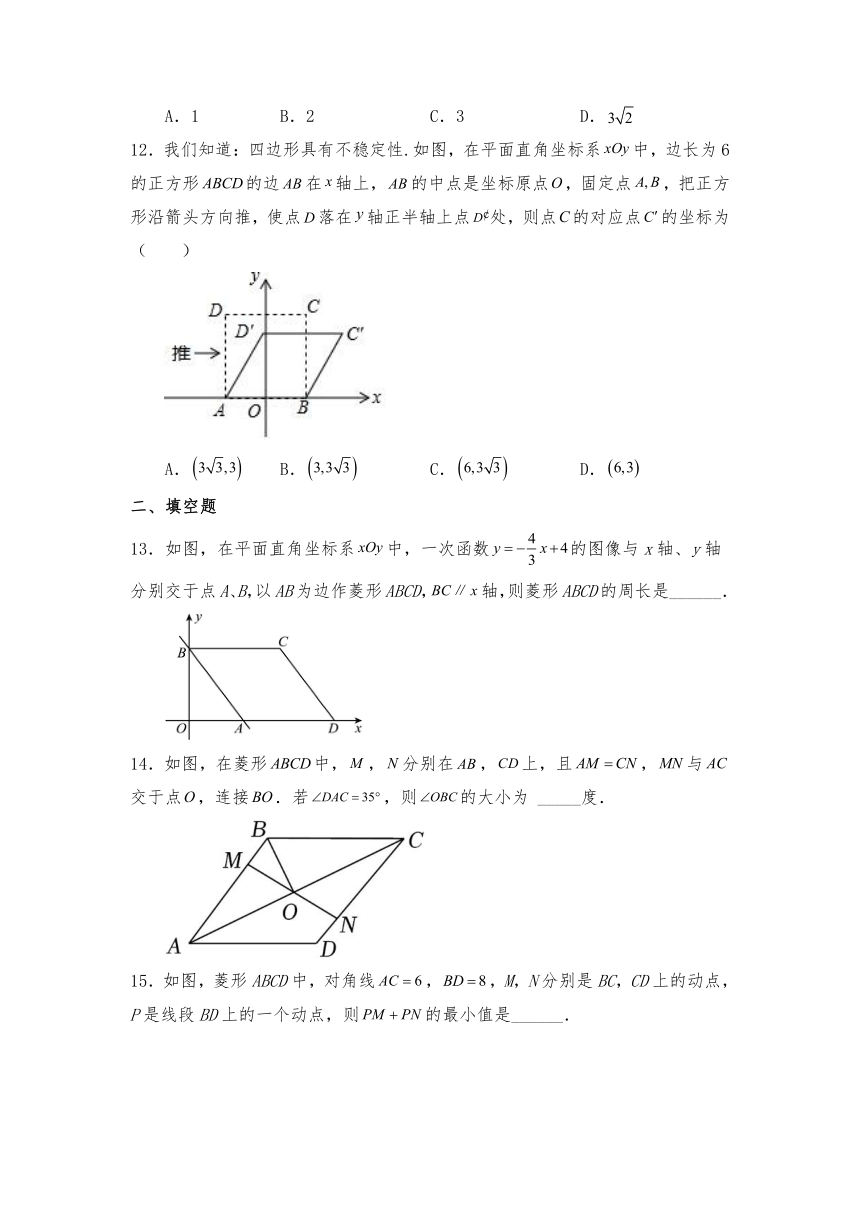
13.如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,以AB为边作菱形ABCD,轴,则菱形ABCD的周长是______.
14.如图,在菱形中,,分别在,上,且,与交于点,连接.若,则的大小为 _____度.
15.如图,菱形ABCD中,对角线,,M,N分别是BC,CD上的动点,P是线段BD上的一个动点,则的最小值是______.
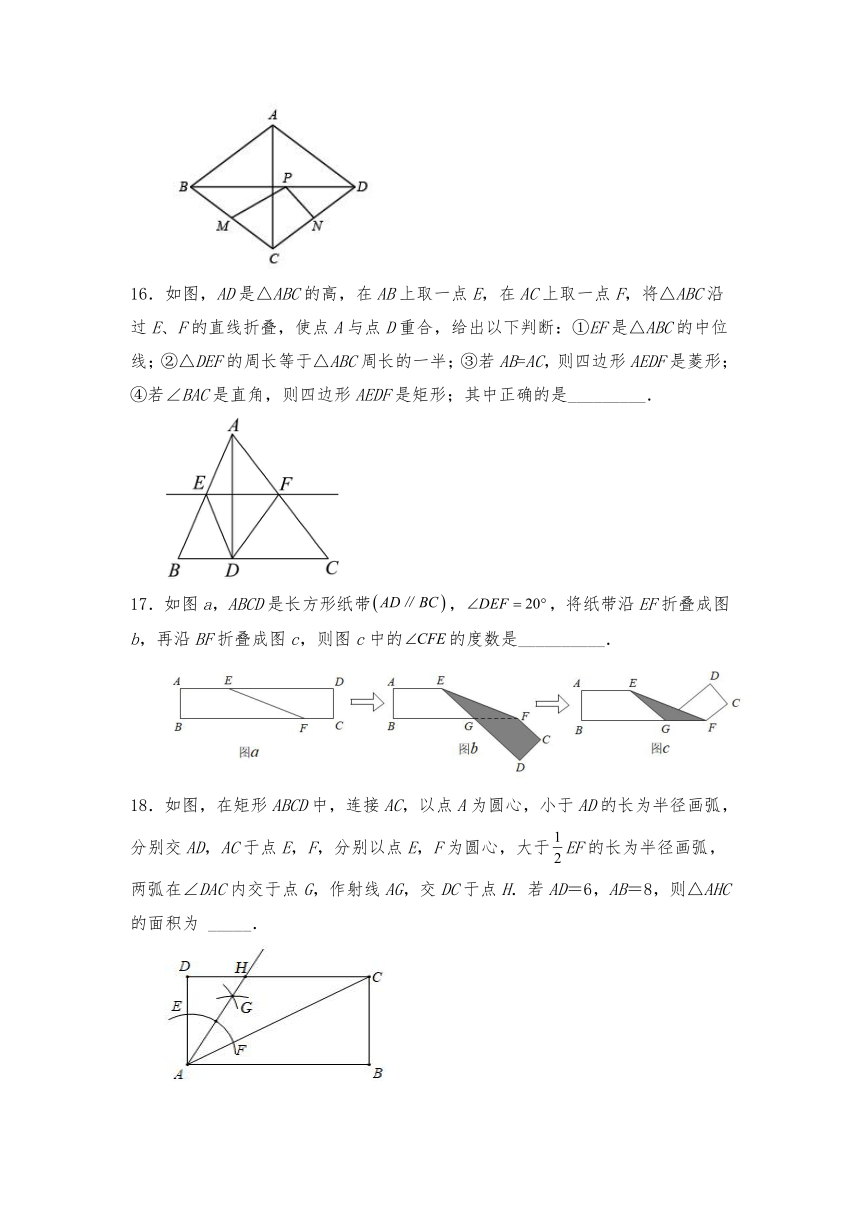
16.如图,AD是△ABC的高,在AB上取一点E,在AC上取一点F,将△ABC沿过E、F的直线折叠,使点A与点D重合,给出以下判断:①EF是△ABC的中位线;②△DEF的周长等于△ABC周长的一半;③若AB=AC,则四边形AEDF是菱形;④若∠BAC是直角,则四边形AEDF是矩形;其中正确的是_________.
17.如图a,ABCD是长方形纸带,,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的的度数是__________.
18.如图,在矩形ABCD中,连接AC,以点A为圆心,小于AD的长为半径画弧,分别交AD,AC于点E,F,分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠DAC内交于点G,作射线AG,交DC于点H.若AD=6,AB=8,则△AHC的面积为 _____.
19.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加一个条件 _____,能使四边形EFGH是矩形.
20.如图,矩形中,,点是的中点,将沿折叠后得到,延长交于点,则的长为________.
21.如图,正方形中,,点E在边上,且.将沿对折至,延长交边于点G,连接,则下列结论:①;②③;④AG//CF;其中正确的有_________(填序号).
22.如图,直线经过正方形的顶点,分别过点、作于点,于点,若,,则的长为________.
23.如图,在四边形中,,点,,,分别是,,,的中点,若,,则四边形的面积是______.
24.如图,点E是正方形ABCD边BC上一点,连接AE,将△ABE绕着点A逆时针旋转到△AFG的位置(点F在正方形ABCD内部),连接DG.若AB=10,BE=6,,则CH=___.
三、解答题
25.如图,在平面直角坐标系中,点是坐标原点,四边形是菱形,点的坐标为,点在轴的正半轴上,直线交轴于点,边交轴于点,连接.
(1)填空:菱形的边长_________;
(2)求直线的解析式;
(3)动点从点出发,沿折线方向以3个单位/秒的速度向终点匀速运动,设的面积为,点的运动时间为秒,
①当时,求与之间的函数关系式;
②在点运动过程中,当,请直接写出的值.
26.如图,在矩形中,,,点从点出发向点运动,同时,点从点出发向点运动,当点运动到点时,两点都停止.连接、、,设点、运动的时间为秒.
(1)若、的速度都为每秒1个单位.当________时,四边形为菱形;
(2)若的速度为每秒3个单位,的速度为每秒1个单位.
①当________时,四边形是矩形;
②当为何值时,线段长为12,请说明理由.
27.综合与实践
如图1,正方形的对角线与交于点,,两边分别与,交于点,.
(1)与的数量关系为______;(直接写出答案)
(2)如图2,点是正方形对角线上一点,,经过点,交于点,连接.猜想线段与的数量关系,并说明理由;
(3)如图3,在图2的基础上,连接,点是的中点,分别连接,.判断的形状,并说明理由.
28.阅读下列材料并完成相应的任务
等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题.在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
如图,矩形的边上有一动点,以为边作,且边过矩形的顶点,在点从点移动到点的过程中,的面积如何变化?
小亮的观点:过点作于点,连接.与的乘积始终等于,所以的面积不变.
小明的观点:在点的运动过程中,的长度在变化,而与两条平行线间的距离不变,所以的面积变化.
任务:你认为小亮和小明谁的观点正确?正确的写出完整的证明过程.
答案
一、单选题
1.D 2.C 3.D 4.D 5.D 6.D
7.D 8.C 9.C 10.C 11.D 12.C
二、填空题
13.20
14.
15.
16.①②③
17.120°
18.15
19.AC⊥BD
20.
21.①②③④
22.9
23.12
24.
三、解答题
25.
(1)解:点的坐标为,
在Rt△AOH中
,
故答案为:5;
(2)∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,
得,
解得,
直线AC的解析式为,
(3)由,令,,则,则,
①当0BP=BA-AP=5-3t,HM=OH-OM=,
,
,
②设M到直线BC的距离为h,
S△ABC=S△AMB+SBMC,
,
解得,
当时,,,
,
当时,代入,
解得,
代入,
解得,
综上所述或.
26.
(1)解:设秒后,四边形是菱形
当,即时,四边形为菱形.
解得:.
故答案为8.4;
(2)解:在矩形中,,,
AD∥BC,AB∥CD,,
当时,
四边形为平行四边形,
,
四边形为矩形,
故 ,
,
故答案为5;
②当点在点的右上方时,
如图1所示:作于,
则,,,
由勾股定理,得,
,
∴,
解得.
当点在点的左上方时,如图2所示,
,,
∴.
在中,由勾股定理得,
∴,解得.
∵运动到时,两点都停止,
∴,解得,
∴,不符合题意.
综上所述,长为12时,值为.
27.
(1)解:;
证明:∵四边形是正方形
∴∠OAE=∠OBF=45°,OA=OB,∠AOB=90°
∵
∴∠AOE=∠BOF
∴(ASA)
(2)解:方法一:
,理由如下:
过点作于点,于点
∵四边形是正方形∴,,平分,
∴,
∵,∴
∴
∵∴
∴
在和中,
∴
∴.
在和中,
∴∴
∴
方法二:,理由如下:
在正方形中,,,平分
∴
在和中,
∴
在四边形中,,
∵
∴
∴
∴
(3)解:是等腰三角形理由如下:
在中,点是的中点,∴
在中,点是的中点,∴
∴
∴是等腰三角形
28.
解:小亮的观点正确.
如图:连接DE,过点E作EM⊥CD于M,则是矩形,
∴EM=AD,
∵,
∴EC·DH为定值,
又,
∴值不变,
故同意小亮的观点.
一、单选题
1.在一组对边平行的四边形中,增加一个条件,使得这个四边形是菱形,那么增加的条件可以是( )
A.另一组对边相等,对角线相等 B.另一组对边相等,对角线互相垂直
C.另一组对边平行,对角线相等 D.另一组对边平行,对角线相互垂直
2.若菱形的两条对角线长分别为6和8,则它的周长为( )
A.14 B.16 C.20 D.24
3.如图,菱形中,,,于点,则( )
A.24 B.10 C. D.
4.如图,在菱形ABCD中,∠B=60°,E是BC的中点,连接AE,DE,DE与AC交于点G、以DE为边作等边三角形DEF,连接AF交DE于点N,交DC于点M.下列结论:①;②∠EAN=45°;③;④点M为AF的中点.其中结论正确的序号有( )
A.①②③ B.①②④ C.②③④ D.①③④
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,BC=2AB=8,点P是BC上一点,PE⊥AC于点E,PF⊥BD于点F,若m=PE+PF,则m的值为( ).
A. B. C. D.
6.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
7.如图,菱形的对角线相交于点O,点P为边上一动点(不与点A,B重合),于点E,于点F.若,,则的最小值为( )
A. B. C.4 D.
8.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
9.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB与点F,EG⊥BC与点G,连接DE,FG,下列结论:①DE=FG,②DE⊥FG,③∠BFG=∠ADE,④FG的最小值为3,其中正确的结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形的顶点,的坐标分别是,,则顶点的坐标是( )
A. B. C. D.
11.如图,四边形,都是正方形,点E,G分别在边,上,连接,过点E作交于点H.若,,则的长为( )
A.1 B.2 C.3 D.
12.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为6的正方形的边在轴上,的中点是坐标原点,固定点,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为( )
A. B. C. D.
二、填空题
13.如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,以AB为边作菱形ABCD,轴,则菱形ABCD的周长是______.
14.如图,在菱形中,,分别在,上,且,与交于点,连接.若,则的大小为 _____度.
15.如图,菱形ABCD中,对角线,,M,N分别是BC,CD上的动点,P是线段BD上的一个动点,则的最小值是______.
16.如图,AD是△ABC的高,在AB上取一点E,在AC上取一点F,将△ABC沿过E、F的直线折叠,使点A与点D重合,给出以下判断:①EF是△ABC的中位线;②△DEF的周长等于△ABC周长的一半;③若AB=AC,则四边形AEDF是菱形;④若∠BAC是直角,则四边形AEDF是矩形;其中正确的是_________.
17.如图a,ABCD是长方形纸带,,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的的度数是__________.
18.如图,在矩形ABCD中,连接AC,以点A为圆心,小于AD的长为半径画弧,分别交AD,AC于点E,F,分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠DAC内交于点G,作射线AG,交DC于点H.若AD=6,AB=8,则△AHC的面积为 _____.
19.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加一个条件 _____,能使四边形EFGH是矩形.
20.如图,矩形中,,点是的中点,将沿折叠后得到,延长交于点,则的长为________.
21.如图,正方形中,,点E在边上,且.将沿对折至,延长交边于点G,连接,则下列结论:①;②③;④AG//CF;其中正确的有_________(填序号).
22.如图,直线经过正方形的顶点,分别过点、作于点,于点,若,,则的长为________.
23.如图,在四边形中,,点,,,分别是,,,的中点,若,,则四边形的面积是______.
24.如图,点E是正方形ABCD边BC上一点,连接AE,将△ABE绕着点A逆时针旋转到△AFG的位置(点F在正方形ABCD内部),连接DG.若AB=10,BE=6,,则CH=___.
三、解答题
25.如图,在平面直角坐标系中,点是坐标原点,四边形是菱形,点的坐标为,点在轴的正半轴上,直线交轴于点,边交轴于点,连接.
(1)填空:菱形的边长_________;
(2)求直线的解析式;
(3)动点从点出发,沿折线方向以3个单位/秒的速度向终点匀速运动,设的面积为,点的运动时间为秒,
①当时,求与之间的函数关系式;
②在点运动过程中,当,请直接写出的值.
26.如图,在矩形中,,,点从点出发向点运动,同时,点从点出发向点运动,当点运动到点时,两点都停止.连接、、,设点、运动的时间为秒.
(1)若、的速度都为每秒1个单位.当________时,四边形为菱形;
(2)若的速度为每秒3个单位,的速度为每秒1个单位.
①当________时,四边形是矩形;
②当为何值时,线段长为12,请说明理由.
27.综合与实践
如图1,正方形的对角线与交于点,,两边分别与,交于点,.
(1)与的数量关系为______;(直接写出答案)
(2)如图2,点是正方形对角线上一点,,经过点,交于点,连接.猜想线段与的数量关系,并说明理由;
(3)如图3,在图2的基础上,连接,点是的中点,分别连接,.判断的形状,并说明理由.
28.阅读下列材料并完成相应的任务
等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题.在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
如图,矩形的边上有一动点,以为边作,且边过矩形的顶点,在点从点移动到点的过程中,的面积如何变化?
小亮的观点:过点作于点,连接.与的乘积始终等于,所以的面积不变.
小明的观点:在点的运动过程中,的长度在变化,而与两条平行线间的距离不变,所以的面积变化.
任务:你认为小亮和小明谁的观点正确?正确的写出完整的证明过程.
答案
一、单选题
1.D 2.C 3.D 4.D 5.D 6.D
7.D 8.C 9.C 10.C 11.D 12.C
二、填空题
13.20
14.
15.
16.①②③
17.120°
18.15
19.AC⊥BD
20.
21.①②③④
22.9
23.12
24.
三、解答题
25.
(1)解:点的坐标为,
在Rt△AOH中
,
故答案为:5;
(2)∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,
得,
解得,
直线AC的解析式为,
(3)由,令,,则,则,
①当0
,
,
②设M到直线BC的距离为h,
S△ABC=S△AMB+SBMC,
,
解得,
当时,,,
,
当时,代入,
解得,
代入,
解得,
综上所述或.
26.
(1)解:设秒后,四边形是菱形
当,即时,四边形为菱形.
解得:.
故答案为8.4;
(2)解:在矩形中,,,
AD∥BC,AB∥CD,,
当时,
四边形为平行四边形,
,
四边形为矩形,
故 ,
,
故答案为5;
②当点在点的右上方时,
如图1所示:作于,
则,,,
由勾股定理,得,
,
∴,
解得.
当点在点的左上方时,如图2所示,
,,
∴.
在中,由勾股定理得,
∴,解得.
∵运动到时,两点都停止,
∴,解得,
∴,不符合题意.
综上所述,长为12时,值为.
27.
(1)解:;
证明:∵四边形是正方形
∴∠OAE=∠OBF=45°,OA=OB,∠AOB=90°
∵
∴∠AOE=∠BOF
∴(ASA)
(2)解:方法一:
,理由如下:
过点作于点,于点
∵四边形是正方形∴,,平分,
∴,
∵,∴
∴
∵∴
∴
在和中,
∴
∴.
在和中,
∴∴
∴
方法二:,理由如下:
在正方形中,,,平分
∴
在和中,
∴
在四边形中,,
∵
∴
∴
∴
(3)解:是等腰三角形理由如下:
在中,点是的中点,∴
在中,点是的中点,∴
∴
∴是等腰三角形
28.
解:小亮的观点正确.
如图:连接DE,过点E作EM⊥CD于M,则是矩形,
∴EM=AD,
∵,
∴EC·DH为定值,
又,
∴值不变,
故同意小亮的观点.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
