八年级数学 下册试题 4.2.1 平行四边形--角平分线-浙教版(含答案)
文档属性
| 名称 | 八年级数学 下册试题 4.2.1 平行四边形--角平分线-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 489.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
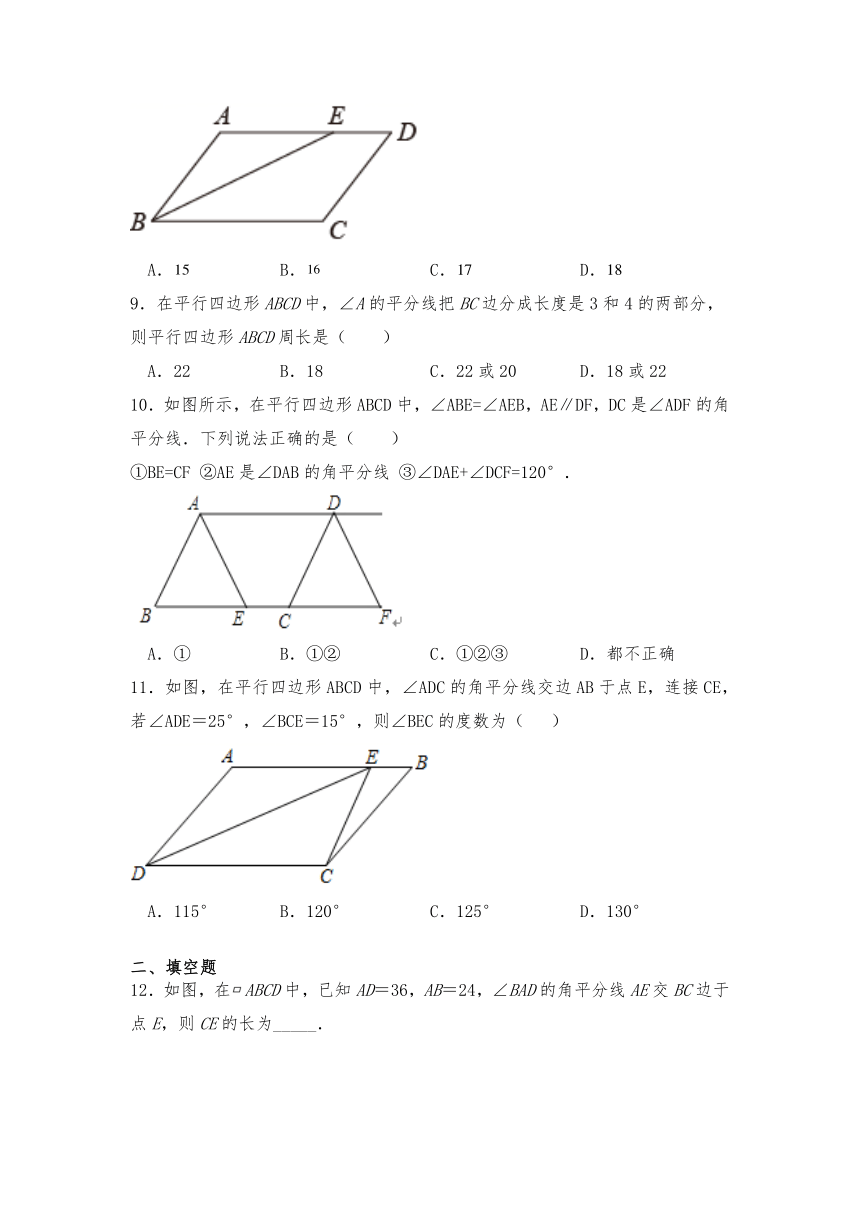
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 09:04:45 | ||
图片预览



文档简介
4.2.1 平行四边形--角平分线
一、单选题
1.如图,在平行四边形中,,平分交边于点E,且,则的长为( )
A.2 B.6 C. D.3
2.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
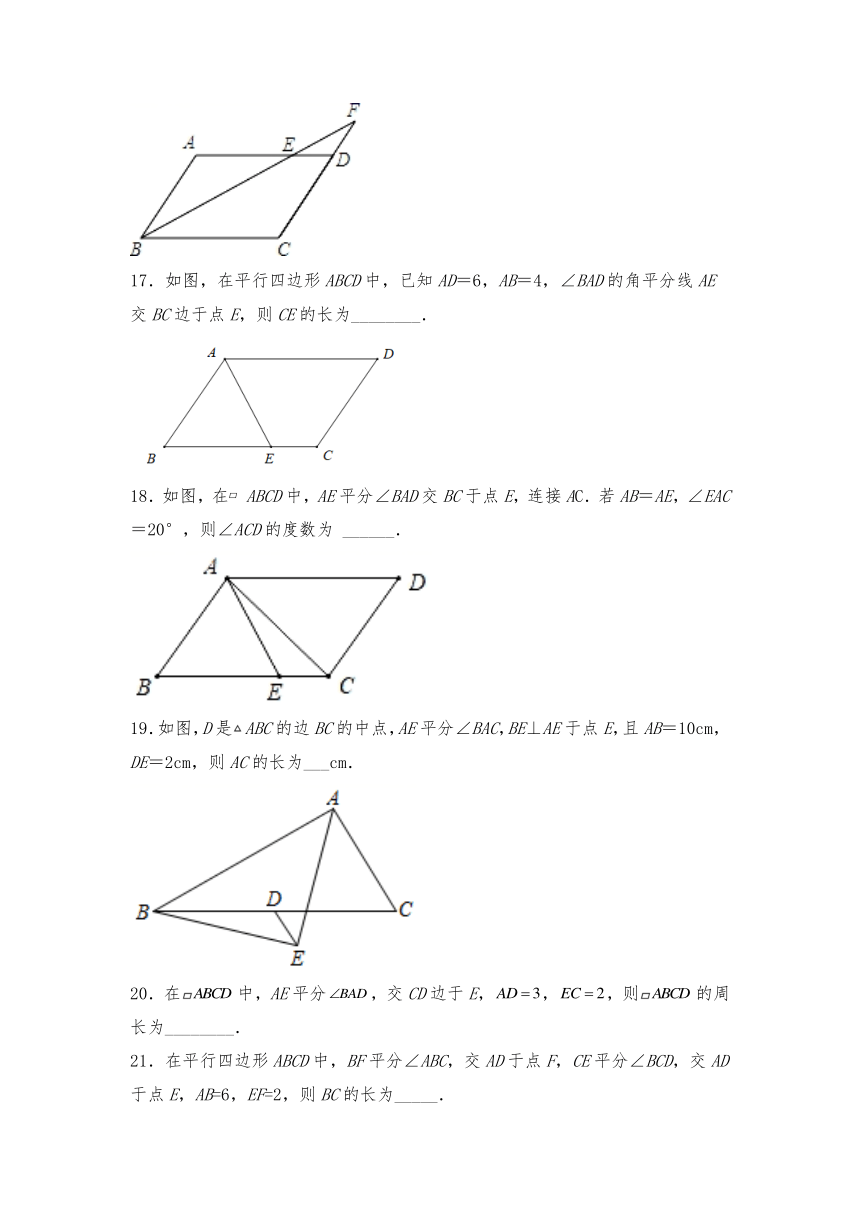
3.在平行四边形中,的角平分线与边所在直线交于点,若,,则平行四边形的周长为( )
A.22 B.16 C.22或18 D.24或16
4.已知四边形是平行四边形,以点为圆心作弧,分别交,于点,再分别以,为圆心,以大于为半径作弧,交于点,射线,交于点,若,,则的长为( )
A.1 B. C. D.2
5.□ABCD的对角线AC、BD相交于点O,AE平分∠BAD交BC于点E, 且∠ADC=60°,AB=BC,连接OE.
有下列结论:①∠CAD=30°; ②S□ABCD = AB·AC ; ③OB=AB; ④OE=AB.其中成立的有( ).
A.1个 B.2个 C.3个 D.4个
6.如图,在平行四边形中,已知,,平分交边于点,则等于( )
A. B. C. D.
7.如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.连接BE,若BE⊥AF,EF=2,,则的长为( )
A. B. C. D.
8.如图在中,的角平分线交于,若,,则平行四边形的周长为( )
A. B. C. D.
9.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
A.22 B.18 C.22或20 D.18或22
10.如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.
A.① B.①② C.①②③ D.都不正确
11.如图,在平行四边形ABCD中,∠ADC的角平分线交边AB于点E,连接CE,若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( )
A.115° B.120° C.125° D.130°
二、填空题
12.如图,在ABCD中,已知AD=36,AB=24,∠BAD的角平分线AE交BC边于点E,则CE的长为_____.
13.如图,是的中位线,平分,交于,若,,则__________.
14.如图,在平行四边形中,,平分交于点,交于点,则∠1=______度.
15.如图,在平行四边形ABCD中,AB=4,BC=6,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为________.
16.如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的角平分线交AD于点E,交CD的延长线于点F,则DE=______cm.
17.如图,在平行四边形ABCD中,已知AD=6,AB=4,∠BAD的角平分线AE交BC边于点E,则CE的长为________.
18.如图,在 ABCD中,AE平分∠BAD交BC于点E,连接AC.若AB=AE,∠EAC=20°,则∠ACD的度数为 ______.
19.如图,D是ABC的边BC的中点,AE平分∠BAC,BE⊥AE于点E,且AB=10cm,DE=2cm,则AC的长为___cm.
20.在中,AE平分,交CD边于E,,,则的周长为________.
21.在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为_____.
22.如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC的角平分线交AD于E,F在AE上,且AF=3,BE与CF交于点G,则EFG与BCG面积之比是_____.
23.平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为_____cm.
24.在平行四边形ABCD中,AD=13,BAD和ADC的角平分线分别交BC于E,F,且EF=6,则平行四边形的周长是____________________
25.如图,在平行四边形中,,,和的角平分线分别交于点E和F,若,则____________
26.如图,点是平行四边形边上一点,将沿直线翻折,点的对应点恰好落在的角平分线上,若,,,则______,______.
三、解答题
27.已知:如图所示,在平行四边形ABCD中DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F
(1)求证:四边形DEBF是平行四边形;
(2)若∠A=60°,AE=2EB,AD=4,求平行四边形ABCD的面积.
28.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:点C是线段BE的中点.
29.如图,在平行四边形ABCD中,点E是BC上一点,∠DAE的角平分线AF交CD于点G,交BC的延长线于点F,连接EG,△AGE的面积为S.
(1)求证:AE=EF;
(2)若EG⊥AF,试探究线段AE,EC,AD之间的数量关系,并说明理由;
(3)在(2)的条件下,若∠AEG=∠AGD,AB=12,AD=9,求S的值.
30.如图,在平行四边形ABCD中,已知AD>AB.
(1)作∠BCD的角平分线交AD于点E,在BC上截取CF=CD(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接EF,猜想四边形CDEF的形状,并证明你的结论.
答案
一、单选题
1.D 2.C 3.C 4.D 5.C 6.B 7.D 8.B 9.C 10.C 11.A
二、填空题
12.12
13.3
14.50
15.2
16.3
17.2
18.80°
19.6
20.16
21.10或14或10
22..
23.32或34
24.45或33.
25.8
26.1
三、解答题
27.
(1)证明:四边形是平行四边形,
.
又,分别是,的平分线,
.
,
,
,
,
,,
四边形是平行四边形;
(2)解:,AB//CD,
,
DE是∠ADC的角平分线,
,
为等边三角形,
,
,
,
过点作于点,
,
,
在中
,
,
,
,
在中,,,
,
,
平行四边形的面积.
28.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴AD=CE,
又∵AD=BC
∴BC=CE,
∴点C是线段BE的中点.
29.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAG=∠F.
∵AF平分∠DAE,
∴∠DAG=∠EAF.
∴∠EAF=∠F.
∴AE=EF.
(2)解:AE=EC+AD;理由是:
∵AE=EF,EG⊥AF,
∴AG=FG.
∵AD∥BC,
∴∠D=∠FCG.
又∵∠AGD=∠FGC,
∴△AGD≌△FGC.
∴AD=FC.
∴EF=EC+FC=EC+AD.
∴AE=EC+AD.
(3)解:∵EG⊥AF,
∴∠AGE=90°.
∴∠AEG+∠EAG=90°.
∵∠DAG=∠EAG,∠AEG=∠AGD,
∴∠AGD+∠DAG=90°.
∴∠D=90°.
∴平行四边形ABCD是矩形.
∴∠B=∠BCD=90°,CD=AB=12,BC=AD=9.
∵△AGD≌△FGC,
∴CG=DG=6,CF=AD=9.
设CE=x,则EF=9+x=AE,BE=9-x,
在Rt△ABE中,由勾股定理得:122+(9-x)2=(9+x)2,
解得x=4,
∴EF=9+x=13.
∵AG=FG,
∴S=S△EFG=EF CG=×13×6=39.
30.
【小题1】
解:如图,射线CE,线段CF即为所求.
【小题2】
结论:四边形CDEF是菱形.
理由:∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DEC=∠ECF,
∵CE平分∠DCB,
∴∠DCE=∠ECF,
∴∠DEC=∠DCE,
∴DE=CD,
∵CF=CD,
∴DE=CF,
∵DE∥CF,
∴四边形CDEF是平行四边形,
∵CD=CF,
∴四边形CDEF是菱形.
一、单选题
1.如图,在平行四边形中,,平分交边于点E,且,则的长为( )
A.2 B.6 C. D.3
2.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
3.在平行四边形中,的角平分线与边所在直线交于点,若,,则平行四边形的周长为( )
A.22 B.16 C.22或18 D.24或16
4.已知四边形是平行四边形,以点为圆心作弧,分别交,于点,再分别以,为圆心,以大于为半径作弧,交于点,射线,交于点,若,,则的长为( )
A.1 B. C. D.2
5.□ABCD的对角线AC、BD相交于点O,AE平分∠BAD交BC于点E, 且∠ADC=60°,AB=BC,连接OE.
有下列结论:①∠CAD=30°; ②S□ABCD = AB·AC ; ③OB=AB; ④OE=AB.其中成立的有( ).
A.1个 B.2个 C.3个 D.4个
6.如图,在平行四边形中,已知,,平分交边于点,则等于( )
A. B. C. D.
7.如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.连接BE,若BE⊥AF,EF=2,,则的长为( )
A. B. C. D.
8.如图在中,的角平分线交于,若,,则平行四边形的周长为( )
A. B. C. D.
9.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
A.22 B.18 C.22或20 D.18或22
10.如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.
A.① B.①② C.①②③ D.都不正确
11.如图,在平行四边形ABCD中,∠ADC的角平分线交边AB于点E,连接CE,若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( )
A.115° B.120° C.125° D.130°
二、填空题
12.如图,在ABCD中,已知AD=36,AB=24,∠BAD的角平分线AE交BC边于点E,则CE的长为_____.
13.如图,是的中位线,平分,交于,若,,则__________.
14.如图,在平行四边形中,,平分交于点,交于点,则∠1=______度.
15.如图,在平行四边形ABCD中,AB=4,BC=6,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为________.
16.如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的角平分线交AD于点E,交CD的延长线于点F,则DE=______cm.
17.如图,在平行四边形ABCD中,已知AD=6,AB=4,∠BAD的角平分线AE交BC边于点E,则CE的长为________.
18.如图,在 ABCD中,AE平分∠BAD交BC于点E,连接AC.若AB=AE,∠EAC=20°,则∠ACD的度数为 ______.
19.如图,D是ABC的边BC的中点,AE平分∠BAC,BE⊥AE于点E,且AB=10cm,DE=2cm,则AC的长为___cm.
20.在中,AE平分,交CD边于E,,,则的周长为________.
21.在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为_____.
22.如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC的角平分线交AD于E,F在AE上,且AF=3,BE与CF交于点G,则EFG与BCG面积之比是_____.
23.平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为_____cm.
24.在平行四边形ABCD中,AD=13,BAD和ADC的角平分线分别交BC于E,F,且EF=6,则平行四边形的周长是____________________
25.如图,在平行四边形中,,,和的角平分线分别交于点E和F,若,则____________
26.如图,点是平行四边形边上一点,将沿直线翻折,点的对应点恰好落在的角平分线上,若,,,则______,______.
三、解答题
27.已知:如图所示,在平行四边形ABCD中DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F
(1)求证:四边形DEBF是平行四边形;
(2)若∠A=60°,AE=2EB,AD=4,求平行四边形ABCD的面积.
28.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:点C是线段BE的中点.
29.如图,在平行四边形ABCD中,点E是BC上一点,∠DAE的角平分线AF交CD于点G,交BC的延长线于点F,连接EG,△AGE的面积为S.
(1)求证:AE=EF;
(2)若EG⊥AF,试探究线段AE,EC,AD之间的数量关系,并说明理由;
(3)在(2)的条件下,若∠AEG=∠AGD,AB=12,AD=9,求S的值.
30.如图,在平行四边形ABCD中,已知AD>AB.
(1)作∠BCD的角平分线交AD于点E,在BC上截取CF=CD(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接EF,猜想四边形CDEF的形状,并证明你的结论.
答案
一、单选题
1.D 2.C 3.C 4.D 5.C 6.B 7.D 8.B 9.C 10.C 11.A
二、填空题
12.12
13.3
14.50
15.2
16.3
17.2
18.80°
19.6
20.16
21.10或14或10
22..
23.32或34
24.45或33.
25.8
26.1
三、解答题
27.
(1)证明:四边形是平行四边形,
.
又,分别是,的平分线,
.
,
,
,
,
,,
四边形是平行四边形;
(2)解:,AB//CD,
,
DE是∠ADC的角平分线,
,
为等边三角形,
,
,
,
过点作于点,
,
,
在中
,
,
,
,
在中,,,
,
,
平行四边形的面积.
28.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴AD=CE,
又∵AD=BC
∴BC=CE,
∴点C是线段BE的中点.
29.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAG=∠F.
∵AF平分∠DAE,
∴∠DAG=∠EAF.
∴∠EAF=∠F.
∴AE=EF.
(2)解:AE=EC+AD;理由是:
∵AE=EF,EG⊥AF,
∴AG=FG.
∵AD∥BC,
∴∠D=∠FCG.
又∵∠AGD=∠FGC,
∴△AGD≌△FGC.
∴AD=FC.
∴EF=EC+FC=EC+AD.
∴AE=EC+AD.
(3)解:∵EG⊥AF,
∴∠AGE=90°.
∴∠AEG+∠EAG=90°.
∵∠DAG=∠EAG,∠AEG=∠AGD,
∴∠AGD+∠DAG=90°.
∴∠D=90°.
∴平行四边形ABCD是矩形.
∴∠B=∠BCD=90°,CD=AB=12,BC=AD=9.
∵△AGD≌△FGC,
∴CG=DG=6,CF=AD=9.
设CE=x,则EF=9+x=AE,BE=9-x,
在Rt△ABE中,由勾股定理得:122+(9-x)2=(9+x)2,
解得x=4,
∴EF=9+x=13.
∵AG=FG,
∴S=S△EFG=EF CG=×13×6=39.
30.
【小题1】
解:如图,射线CE,线段CF即为所求.
【小题2】
结论:四边形CDEF是菱形.
理由:∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DEC=∠ECF,
∵CE平分∠DCB,
∴∠DCE=∠ECF,
∴∠DEC=∠DCE,
∴DE=CD,
∵CF=CD,
∴DE=CF,
∵DE∥CF,
∴四边形CDEF是平行四边形,
∵CD=CF,
∴四边形CDEF是菱形.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
