八年级数学 下册试题 《平行四边形》全章复习-浙教版(含答案)
文档属性
| 名称 | 八年级数学 下册试题 《平行四边形》全章复习-浙教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 839.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 00:00:00 | ||
图片预览

文档简介
《平行四边形》全章复习
一、单选题
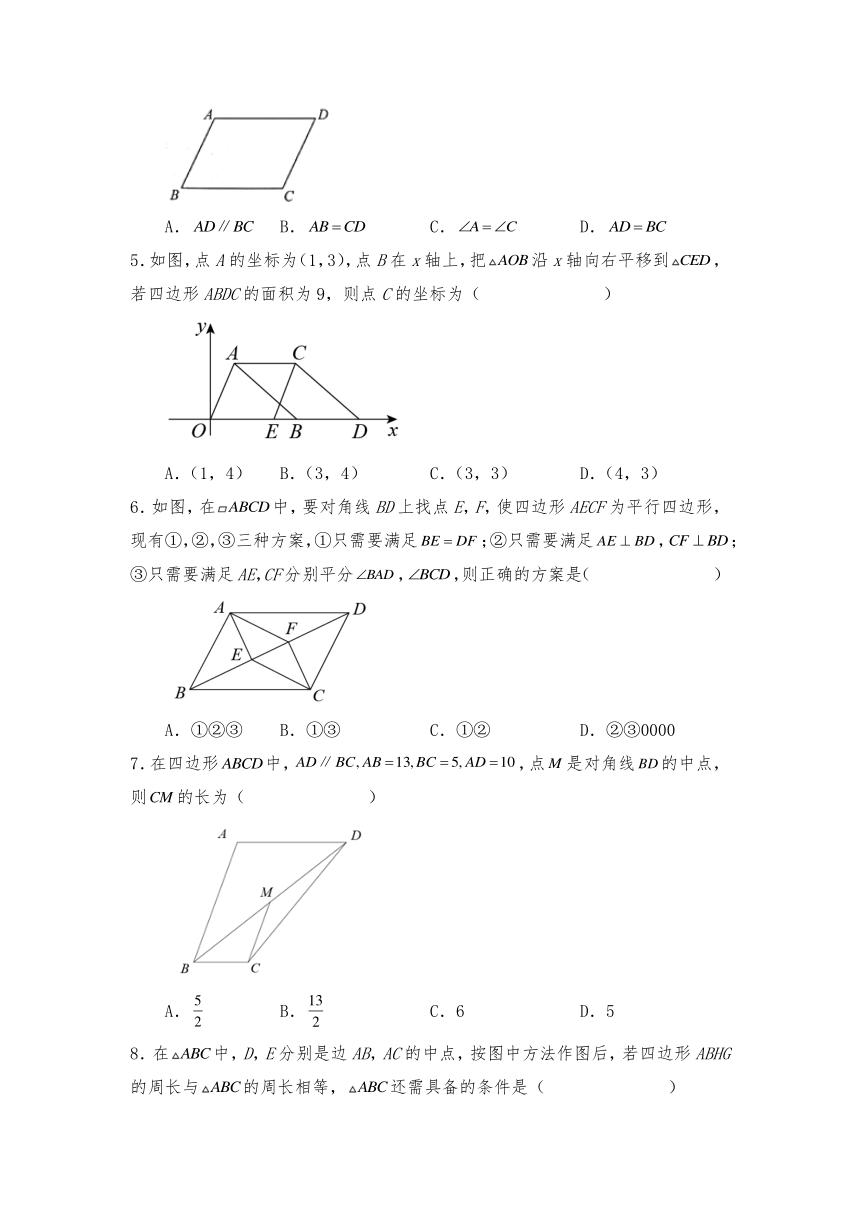
1.如图,EF过平行四边形ABCD的对角线的交点O,交AD于E,交BC于F,若AB=4,BC=5,OE=2.5,那么四边形EFCD的周长是( )
A.9 B.10.5 C.12 D.14
2.如图所示,在平行四边形中,对角线,相交于点,过点的直线分别交于点,于点,,,则平行四边形的面积( )
A. B. C. D.
3.如图,在平行四边形ABCD中,,,,点E在AB边上,将沿着直线DE翻折得.连结,若点恰好落在的平分线上,则,C两点间的距离为( )
A.3或6 B.3或 C. D.6
4.如图,在四边形中,.添加下列条件后,仍不能判定此四边形为平行四边形的是( )
A. B. C. D.
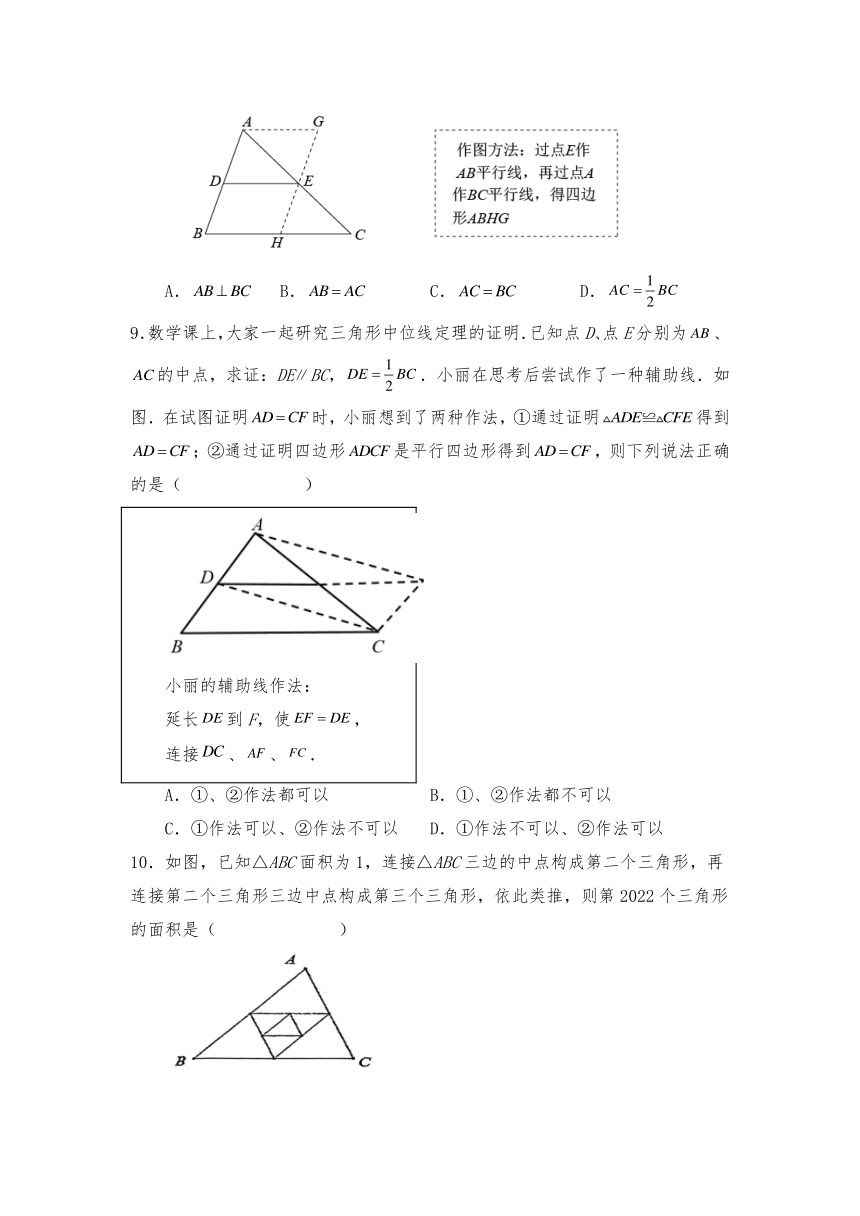
5.如图,点A的坐标为(1,3),点B在x轴上,把沿x轴向右平移到,若四边形ABDC的面积为9,则点C的坐标为( )
A.(1,4) B.(3,4) C.(3,3) D.(4,3)
6.如图,在中,要对角线BD上找点E,F,使四边形AECF为平行四边形,现有①,②,③三种方案,①只需要满足;②只需要满足,;③只需要满足AE,CF分别平分,,则正确的方案是( )
A.①②③ B.①③ C.①② D.②③0000
7.在四边形中,,点是对角线的中点,则的长为( )
A. B. C.6 D.5
8.在中,D,E分别是边AB,AC的中点,按图中方法作图后,若四边形ABHG的周长与的周长相等,还需具备的条件是( )
A. B. C. D.
9.数学课上,大家一起研究三角形中位线定理的证明.已知点D、点E分别为、的中点,求证:DEBC,.小丽在思考后尝试作了一种辅助线.如图.在试图证明时,小丽想到了两种作法,①通过证明得到;②通过证明四边形是平行四边形得到,则下列说法正确的是( )
小丽的辅助线作法: 延长到F,使, 连接、、.
A.①、②作法都可以 B.①、②作法都不可以
C.①作法可以、②作法不可以 D.①作法不可以、②作法可以
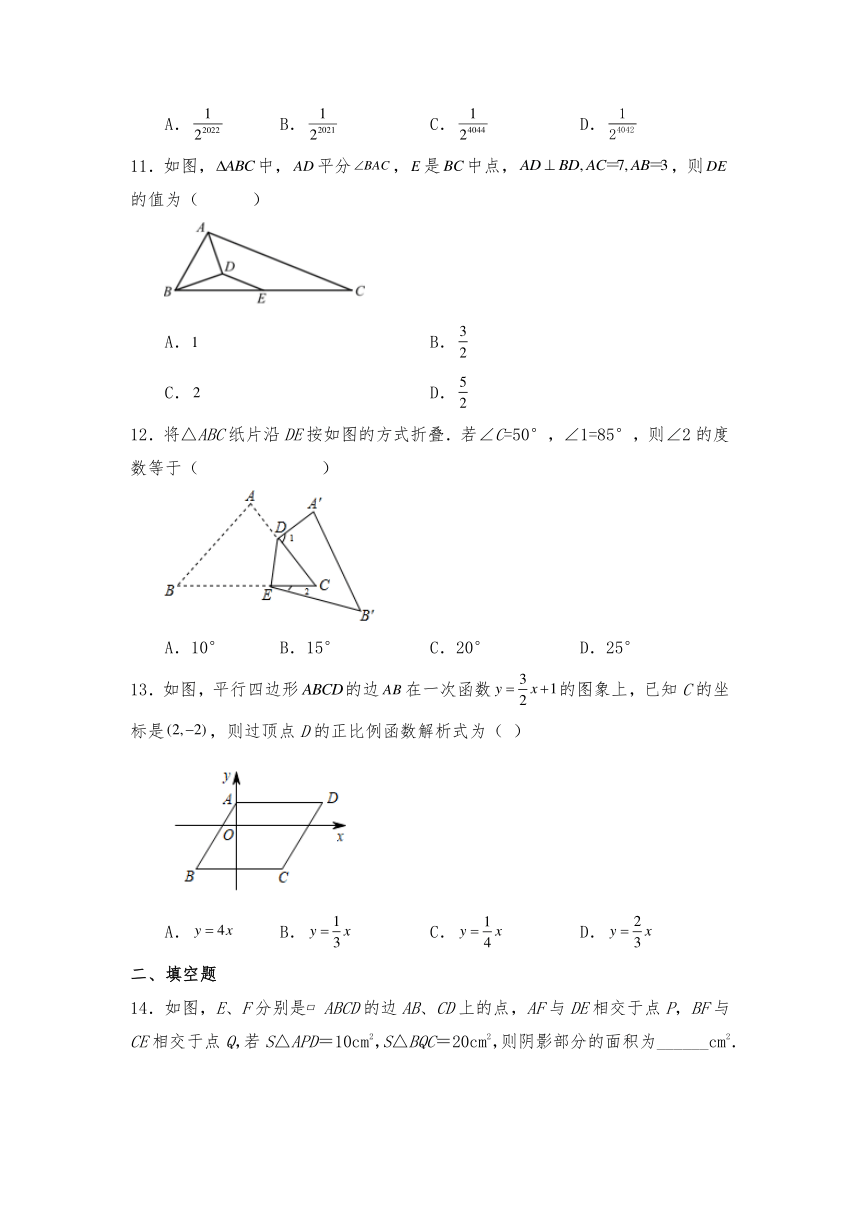
10.如图,已知△ABC面积为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,依此类推,则第2022个三角形的面积是( )
A. B. C. D.
11.如图,中,平分,是中点,,则的值为( )
A. B.
C. D.
12.将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2的度数等于( )
A.10° B.15° C.20° D.25°
13.如图,平行四边形的边在一次函数的图象上,已知C的坐标是,则过顶点D的正比例函数解析式为( )
A. B. C. D.
二、填空题
14.如图,E、F分别是 ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=10cm2,S△BQC=20cm2,则阴影部分的面积为______cm2.
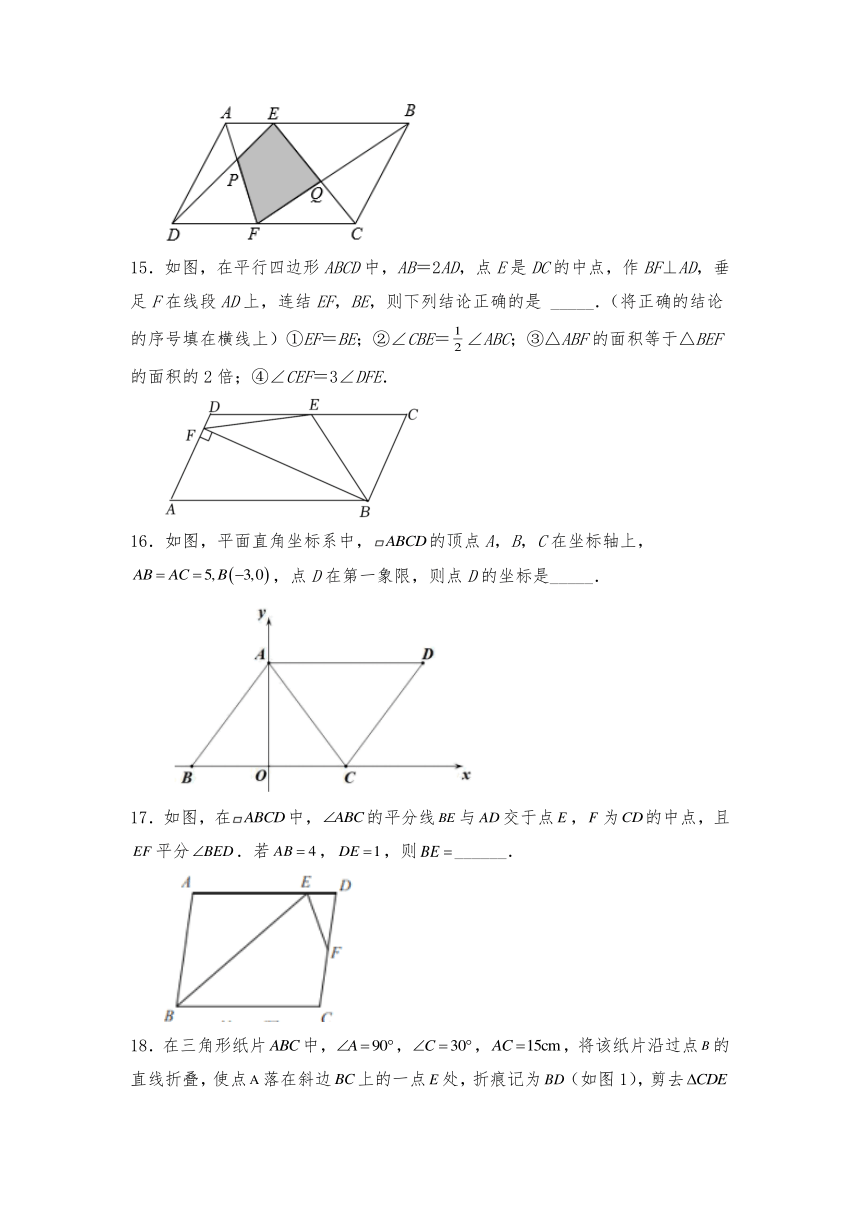
15.如图,在平行四边形ABCD中,AB=2AD,点E是DC的中点,作BF⊥AD,垂足F在线段AD上,连结EF,BE,则下列结论正确的是 _____.(将正确的结论的序号填在横线上)①EF=BE;②∠CBE=∠ABC;③△ABF的面积等于△BEF的面积的2倍;④∠CEF=3∠DFE.
16.如图,平面直角坐标系中,的顶点A,B,C在坐标轴上,,点D在第一象限,则点D的坐标是_____.
17.如图,在中,的平分线与交于点,为的中点,且平分.若,,则______.
18.在三角形纸片中,,,,将该纸片沿过点的直线折叠,使点落在斜边上的一点处,折痕记为(如图1),剪去后得到双层(如图2),再沿着过某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为________.
19.如图,在中,过对角线上一点作,,且, ,则__.
20.在平面直角坐标系中,,,,点在直线上,若以,,,四点为顶点的四边形是平行四边形,则点的坐标为________.
21.如图,在平面直角坐标系中,点在轴上,点在轴上,连接,,过轴上一点作直线,关于直线的对称线段为,若线段和过点且垂直于轴的直线有公共点,则的取值范围是________.
22.如图,在平行四边形ABCD中,,E、F分别在CD和BC的延长线上,,,则______.
23.如图,在 ABCD中,点E是对角线AC上一点,过点E作AC的垂线,交边AD于点P,交边BC于点Q,连接PC、AQ,若AC=6,PQ=4,则PC+AQ的最小值为________________.
24.如图,∠AOB=30°,OA=4,D为OA的中点,点P是射线OB上的一个动点,连结AP,DP,将△ADP沿DP折叠,折叠后得到△DPA',当△DPA'与△ODP的重叠部分的面积恰好为△ODP面积的一半时,OP的长为________.
25.如图,的周长为28,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若,则PQ的长是______.
26.如图,在中,,点,分别从点,同时出发,沿,方向以相同的速度运动(分别运动到点,即停止),与相交于点,与相交于点.则在此运动过程中,线段的长始终等于______.
27.如图,点是的对角线交点,E为CD中点,AE交BD于点F,若,则的值为______.
28.如图,在四边形ABCD中,∠A+∠B=210°,作∠ADC、∠BCD的平分线交于点O1,再作∠O1DC、∠O1CD的平分线交于点O2,则∠O2的度数为_______________.
三、解答题
29.如图,在中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F.
(1)求证:;
(2)若,,,连接DE,求DE的长.
30.如图,在平行四边形ABCD中,点E、F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
(1)求证:EF与GH互相平分;
(2)在不添加任何辅助线和字母的条件下,请直接写出图中所有全等的三角形.
31.在平面直角坐标系中,O为坐标原点.已知两点,且a、b满足;若四边形ABCD为平行四边形,且,点在y轴上.
(1)如图①,动点P从C点出发,以每秒2个单位长度沿y轴向下运动,当时间t为何值时,三角形ABP的面积等于平行四边形ABCD面积的四分之一;
(2)如图②,当P从O点出发,沿y轴向上运动,连接PD、PA,则、、存在的数量关系是______(排除点P在点O和点C两点的特殊情况).
32.如图,在ABCD中,AE⊥BC于点E,BE=3,AB=5,连接AC,点F以每秒1个单位长度的速度由点A向点C匀速运动,到达C点即停止运动,G,H分别是AF,EF的中点,连接GH.设点F运动的时间为t.
(1)判断GH与AE的位置关系和数量关系,并求出GH的长;
(2)若CE=AB.
①求点F由点A向点C匀速运动的过程中,线段GH所扫过区域的面积;
②若△FGH是等腰三角形,求t的值.
答案
一、单选题
1.D 2.B 3.A 4.D 5.D 6.A 7.B 8.B
9.A 10.D 11.C 12.B 13.C
二、填空题
14.30
15.①②④
16.
17.6
18.20或
19.2
20.,,
21.
22.8
23.
24.2或
25.4
26.
27.6
28.
三、解答题
29.
(1)
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
则在△BAE和△CFE中,
,
∴△BAE≌△CFE(),
∴AB=CF,
∴CF=CD;
(2)
由(1)得:CF=CD,△BAE≌△CFE,
∴AE=EF,DF=2CD,
∵AB=CD,
∴DF=2AB,
∵AD=2AB,
∴AD=DF,
∵AE=EF,
∴DE⊥AF
在中,,
∴
30.
(1)
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴四边形AECF是平行四边形.
∴AF∥CE,
∵AE=CF,AB∥CD,AB=CD,
∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,
∴BF∥DE,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分;
(2)
解:∵
∴△ADE≌△CFB(SAS)
∴∠ADE=∠CBF,∠AED=∠CFB,DE=BF
由(1)可知四边形AECF是平行四边形,
∴∠BAF=∠FCE,AF=CE
又∠BAD=∠DCB
∴∠DAF=∠BCE
又∵∠ADE=∠CBF,AD=BC
∴△AHD≌△BGC(AAS)
∴∠AHD=∠BGC
∴∠AHE=∠CGF
∵AB=CD,AF=CE,BF=DE
∴△ABF≌△CDE(SSS)
∵AE=CF,∠AHE=∠CGF,∠AED=∠CFB
∴△AEH≌△CFG(AAS)
∵AD=BC,DF=CD-CF=AB-AE=BE,∠ADF=∠CBA
∴△ADF≌△BEC(SAS)
∵四边形AECF是平行四边形,
∴△AEF≌△CEF
∵四边形BFDE是平行四边形,
∴△DEF≌△BEF,
∵四边形EGFH是平行四边形
∴△EGH≌△FGH,△EFH≌△EFG
因此图中所有的全等的三角形有:△ADE≌△CFB;△AHD≌△BGC;△ABF≌△CDE;△AEH≌△CFG;△ADF≌△BEC;△AEF≌△CEF;△DEF≌△BEF;△EGH≌△FGH;△EFH≌△EFG.
31.
(1)
解:,
,
,
,
,
,
点,
,
,
四边形ABCD是平行四边形,
三角形ABP的面积等于平行四边形ABCD面积的四分之一,
,
解得或3.
当时间t为1或3时,三角形ABP的面积等于平行四边形ABCD面积的四分之一.
(2)
解:如图②,当点P在线段OC上时,,理由如下:
过P作,
,
,
,
,
,
;
如图③,当点P在CD的上面时,,理由如下:
过P作,
,
,
,
,
,
.
32.
(1)
解:∵AE⊥BC于点E,BE=3,AB=5,
∴AE=4,
∵G,H分别是AF,EF的中点,
∴GH∥AE,GH=AE=2;
(2)
解:①∵CE=AB=5,
∴AC=,
取EC的中点M,AC的中点N,AE的中点O,线段GH所扫过区域是 AOMN,
EM=CE=,
∴线段GH所扫过区域的面积=MN EM=GH EM=2×=5;
;
②当FH=FG时,△FGH是等腰三角形,
此时FE=FA,
∴∠FEA=∠FAE,
∵∠FEA+∠FEC=90°,∠FAE+∠FCE=90°,
∴∠FEC=∠FCE,
∴FE=FC,
∴FE=FA=FC,
∴AF=AC=,
∴t的值为(秒);
当GH=FG时,△FGH是等腰三角形,
此时AE=FA=4,
∴t的值为4(秒);
当GH=HF时,△FGH是等腰三角形,
此时AE=EF=4,连接EG,
∵G是AF的中点,
∴EG⊥AC,
∵S△AEC=AE EC=AC EG,
∴EG=,
∴AG=,
∴AF= 2AG,
∴t的值为(秒);
综上,t的值为秒或4秒或秒.
一、单选题
1.如图,EF过平行四边形ABCD的对角线的交点O,交AD于E,交BC于F,若AB=4,BC=5,OE=2.5,那么四边形EFCD的周长是( )
A.9 B.10.5 C.12 D.14
2.如图所示,在平行四边形中,对角线,相交于点,过点的直线分别交于点,于点,,,则平行四边形的面积( )
A. B. C. D.
3.如图,在平行四边形ABCD中,,,,点E在AB边上,将沿着直线DE翻折得.连结,若点恰好落在的平分线上,则,C两点间的距离为( )
A.3或6 B.3或 C. D.6
4.如图,在四边形中,.添加下列条件后,仍不能判定此四边形为平行四边形的是( )
A. B. C. D.
5.如图,点A的坐标为(1,3),点B在x轴上,把沿x轴向右平移到,若四边形ABDC的面积为9,则点C的坐标为( )
A.(1,4) B.(3,4) C.(3,3) D.(4,3)
6.如图,在中,要对角线BD上找点E,F,使四边形AECF为平行四边形,现有①,②,③三种方案,①只需要满足;②只需要满足,;③只需要满足AE,CF分别平分,,则正确的方案是( )
A.①②③ B.①③ C.①② D.②③0000
7.在四边形中,,点是对角线的中点,则的长为( )
A. B. C.6 D.5
8.在中,D,E分别是边AB,AC的中点,按图中方法作图后,若四边形ABHG的周长与的周长相等,还需具备的条件是( )
A. B. C. D.
9.数学课上,大家一起研究三角形中位线定理的证明.已知点D、点E分别为、的中点,求证:DEBC,.小丽在思考后尝试作了一种辅助线.如图.在试图证明时,小丽想到了两种作法,①通过证明得到;②通过证明四边形是平行四边形得到,则下列说法正确的是( )
小丽的辅助线作法: 延长到F,使, 连接、、.
A.①、②作法都可以 B.①、②作法都不可以
C.①作法可以、②作法不可以 D.①作法不可以、②作法可以
10.如图,已知△ABC面积为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,依此类推,则第2022个三角形的面积是( )
A. B. C. D.
11.如图,中,平分,是中点,,则的值为( )
A. B.
C. D.
12.将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2的度数等于( )
A.10° B.15° C.20° D.25°
13.如图,平行四边形的边在一次函数的图象上,已知C的坐标是,则过顶点D的正比例函数解析式为( )
A. B. C. D.
二、填空题
14.如图,E、F分别是 ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=10cm2,S△BQC=20cm2,则阴影部分的面积为______cm2.
15.如图,在平行四边形ABCD中,AB=2AD,点E是DC的中点,作BF⊥AD,垂足F在线段AD上,连结EF,BE,则下列结论正确的是 _____.(将正确的结论的序号填在横线上)①EF=BE;②∠CBE=∠ABC;③△ABF的面积等于△BEF的面积的2倍;④∠CEF=3∠DFE.
16.如图,平面直角坐标系中,的顶点A,B,C在坐标轴上,,点D在第一象限,则点D的坐标是_____.
17.如图,在中,的平分线与交于点,为的中点,且平分.若,,则______.
18.在三角形纸片中,,,,将该纸片沿过点的直线折叠,使点落在斜边上的一点处,折痕记为(如图1),剪去后得到双层(如图2),再沿着过某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为________.
19.如图,在中,过对角线上一点作,,且, ,则__.
20.在平面直角坐标系中,,,,点在直线上,若以,,,四点为顶点的四边形是平行四边形,则点的坐标为________.
21.如图,在平面直角坐标系中,点在轴上,点在轴上,连接,,过轴上一点作直线,关于直线的对称线段为,若线段和过点且垂直于轴的直线有公共点,则的取值范围是________.
22.如图,在平行四边形ABCD中,,E、F分别在CD和BC的延长线上,,,则______.
23.如图,在 ABCD中,点E是对角线AC上一点,过点E作AC的垂线,交边AD于点P,交边BC于点Q,连接PC、AQ,若AC=6,PQ=4,则PC+AQ的最小值为________________.
24.如图,∠AOB=30°,OA=4,D为OA的中点,点P是射线OB上的一个动点,连结AP,DP,将△ADP沿DP折叠,折叠后得到△DPA',当△DPA'与△ODP的重叠部分的面积恰好为△ODP面积的一半时,OP的长为________.
25.如图,的周长为28,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若,则PQ的长是______.
26.如图,在中,,点,分别从点,同时出发,沿,方向以相同的速度运动(分别运动到点,即停止),与相交于点,与相交于点.则在此运动过程中,线段的长始终等于______.
27.如图,点是的对角线交点,E为CD中点,AE交BD于点F,若,则的值为______.
28.如图,在四边形ABCD中,∠A+∠B=210°,作∠ADC、∠BCD的平分线交于点O1,再作∠O1DC、∠O1CD的平分线交于点O2,则∠O2的度数为_______________.
三、解答题
29.如图,在中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F.
(1)求证:;
(2)若,,,连接DE,求DE的长.
30.如图,在平行四边形ABCD中,点E、F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
(1)求证:EF与GH互相平分;
(2)在不添加任何辅助线和字母的条件下,请直接写出图中所有全等的三角形.
31.在平面直角坐标系中,O为坐标原点.已知两点,且a、b满足;若四边形ABCD为平行四边形,且,点在y轴上.
(1)如图①,动点P从C点出发,以每秒2个单位长度沿y轴向下运动,当时间t为何值时,三角形ABP的面积等于平行四边形ABCD面积的四分之一;
(2)如图②,当P从O点出发,沿y轴向上运动,连接PD、PA,则、、存在的数量关系是______(排除点P在点O和点C两点的特殊情况).
32.如图,在ABCD中,AE⊥BC于点E,BE=3,AB=5,连接AC,点F以每秒1个单位长度的速度由点A向点C匀速运动,到达C点即停止运动,G,H分别是AF,EF的中点,连接GH.设点F运动的时间为t.
(1)判断GH与AE的位置关系和数量关系,并求出GH的长;
(2)若CE=AB.
①求点F由点A向点C匀速运动的过程中,线段GH所扫过区域的面积;
②若△FGH是等腰三角形,求t的值.
答案
一、单选题
1.D 2.B 3.A 4.D 5.D 6.A 7.B 8.B
9.A 10.D 11.C 12.B 13.C
二、填空题
14.30
15.①②④
16.
17.6
18.20或
19.2
20.,,
21.
22.8
23.
24.2或
25.4
26.
27.6
28.
三、解答题
29.
(1)
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
则在△BAE和△CFE中,
,
∴△BAE≌△CFE(),
∴AB=CF,
∴CF=CD;
(2)
由(1)得:CF=CD,△BAE≌△CFE,
∴AE=EF,DF=2CD,
∵AB=CD,
∴DF=2AB,
∵AD=2AB,
∴AD=DF,
∵AE=EF,
∴DE⊥AF
在中,,
∴
30.
(1)
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴四边形AECF是平行四边形.
∴AF∥CE,
∵AE=CF,AB∥CD,AB=CD,
∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,
∴BF∥DE,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分;
(2)
解:∵
∴△ADE≌△CFB(SAS)
∴∠ADE=∠CBF,∠AED=∠CFB,DE=BF
由(1)可知四边形AECF是平行四边形,
∴∠BAF=∠FCE,AF=CE
又∠BAD=∠DCB
∴∠DAF=∠BCE
又∵∠ADE=∠CBF,AD=BC
∴△AHD≌△BGC(AAS)
∴∠AHD=∠BGC
∴∠AHE=∠CGF
∵AB=CD,AF=CE,BF=DE
∴△ABF≌△CDE(SSS)
∵AE=CF,∠AHE=∠CGF,∠AED=∠CFB
∴△AEH≌△CFG(AAS)
∵AD=BC,DF=CD-CF=AB-AE=BE,∠ADF=∠CBA
∴△ADF≌△BEC(SAS)
∵四边形AECF是平行四边形,
∴△AEF≌△CEF
∵四边形BFDE是平行四边形,
∴△DEF≌△BEF,
∵四边形EGFH是平行四边形
∴△EGH≌△FGH,△EFH≌△EFG
因此图中所有的全等的三角形有:△ADE≌△CFB;△AHD≌△BGC;△ABF≌△CDE;△AEH≌△CFG;△ADF≌△BEC;△AEF≌△CEF;△DEF≌△BEF;△EGH≌△FGH;△EFH≌△EFG.
31.
(1)
解:,
,
,
,
,
,
点,
,
,
四边形ABCD是平行四边形,
三角形ABP的面积等于平行四边形ABCD面积的四分之一,
,
解得或3.
当时间t为1或3时,三角形ABP的面积等于平行四边形ABCD面积的四分之一.
(2)
解:如图②,当点P在线段OC上时,,理由如下:
过P作,
,
,
,
,
,
;
如图③,当点P在CD的上面时,,理由如下:
过P作,
,
,
,
,
,
.
32.
(1)
解:∵AE⊥BC于点E,BE=3,AB=5,
∴AE=4,
∵G,H分别是AF,EF的中点,
∴GH∥AE,GH=AE=2;
(2)
解:①∵CE=AB=5,
∴AC=,
取EC的中点M,AC的中点N,AE的中点O,线段GH所扫过区域是 AOMN,
EM=CE=,
∴线段GH所扫过区域的面积=MN EM=GH EM=2×=5;
;
②当FH=FG时,△FGH是等腰三角形,
此时FE=FA,
∴∠FEA=∠FAE,
∵∠FEA+∠FEC=90°,∠FAE+∠FCE=90°,
∴∠FEC=∠FCE,
∴FE=FC,
∴FE=FA=FC,
∴AF=AC=,
∴t的值为(秒);
当GH=FG时,△FGH是等腰三角形,
此时AE=FA=4,
∴t的值为4(秒);
当GH=HF时,△FGH是等腰三角形,
此时AE=EF=4,连接EG,
∵G是AF的中点,
∴EG⊥AC,
∵S△AEC=AE EC=AC EG,
∴EG=,
∴AG=,
∴AF= 2AG,
∴t的值为(秒);
综上,t的值为秒或4秒或秒.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
