八年级数学下册试题 6.2 反比例函数的图象和性质-浙教版(含答案)
文档属性
| 名称 | 八年级数学下册试题 6.2 反比例函数的图象和性质-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 767.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 09:40:10 | ||
图片预览




文档简介
6.2 反比例函数的图象和性质
一、单选题
1.如图,点A是反比例函数图象上一点,则下列各点在该函数图象上的是( )
A. B. C. D.
2.运用你学习函数的经验,判断以下哪个函数的图像如图所示( )
A. B. C. D.
3.如图,函数与在同一平面直角坐标系中的大致图象是( )
A. B. C. D.
4.反比例函数(m为常数)的图象在第二、四象限,那么m的取值范围是( )
A. B. C. D.
5.若反比例函数的图象经过点,则它的图象也一定经过的点是( )
A. B. C. D.
6.若点,,在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.已知反比例函数y=的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( ).
A.(-1,2) B.(-2,) C.(-2,3) D.(1,-2)
8.如图所示,直线y=-x与双曲线y=交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,k的值为( )
A.-10 B.-9 C.-6 D.-4
9.如图,在平面直角坐标系中,的顶点在轴正半轴上,是的中线,点、在反比例函数的图象上,则的面积等于( )
A.2 B.3 C.4 D.6
10.如图,在以为原点的直角坐标系中,矩形的两边、分别在轴、轴的正半轴上,反比例函数的图像与相交于点,与相交于点,若,且的面积是,则( )
A. B. C. D.
二、填空题
11.已知正比例函数与反比例函数的图象交于点和点,则点的坐标为________.
12.若反比例函数y=(m≠0)与正比例函数y=7x无交点,则m的取值范围是___________
13.设A(x1,y1),B(x2,y2)为函数图象上的两点,且x1<0<x2,y1>y2,则实数k的取值范围是__.
14.如果反比例函数(k是常数,且)的图象经过点,那么这个反比例函数的图象在第______象限.
15.已知函数,,当时,函数的最大值为,函数的最小值为,则的值为______.
16.反比例函数的图像经过点(3,1)、(,2)、(,3),比较大小:________.
17.如图所示,在平面直角坐标系中,等腰直角三角形的顶点、分别在轴、轴的正半轴上,,轴于点,点在函数的图象上,若,则的值为___.
18.如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若,则________.
三、解答题
19.如图,在平面直角坐标系中,一次函数和的图象相交于点,反比例函数的图象经过点.
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为,连接,求的面积.
20.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点,与轴交于点.
求点的坐标和反比例函数的解析式;
点是反比例函数图象上一点且纵坐标是1,连接,,求的面积.
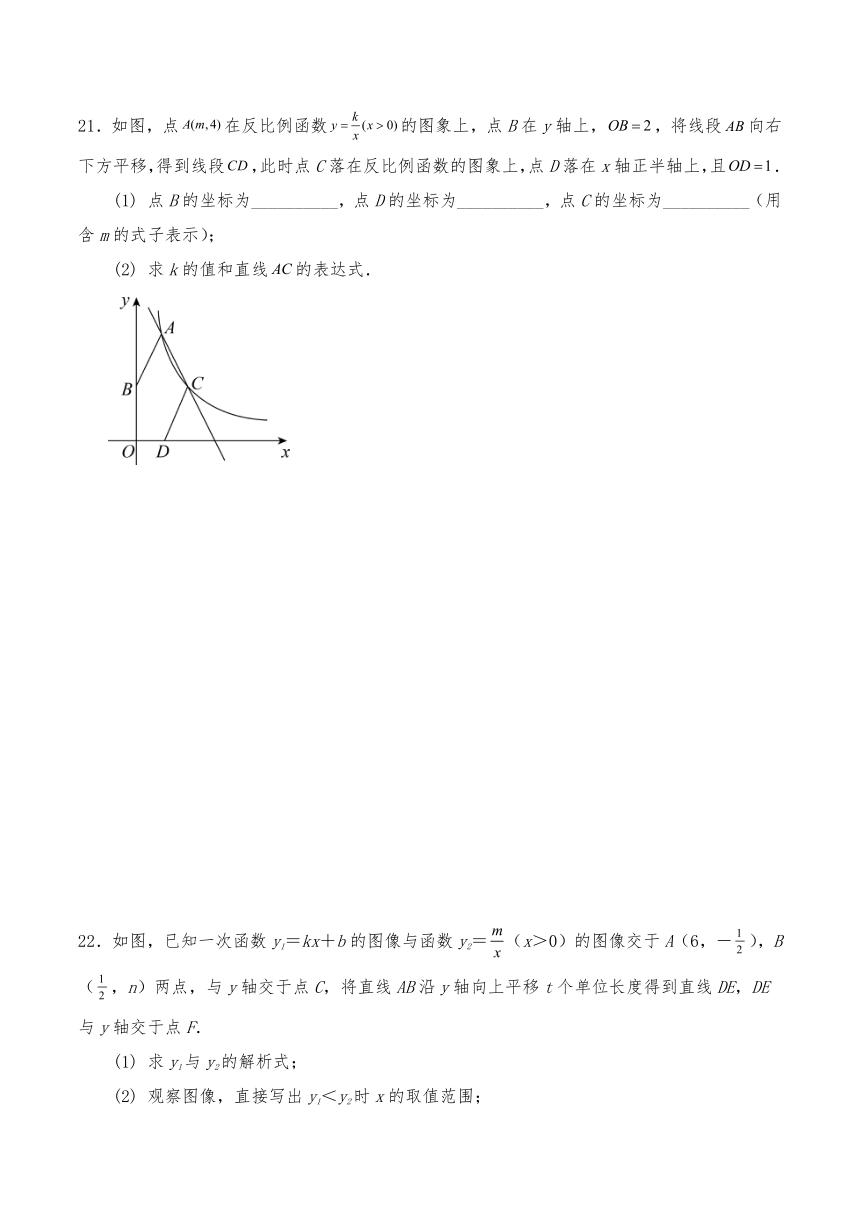
21.如图,点在反比例函数的图象上,点B在y轴上,,将线段向右下方平移,得到线段,此时点C落在反比例函数的图象上,点D落在x轴正半轴上,且.
点B的坐标为__________,点D的坐标为__________,点C的坐标为__________(用含m的式子表示);
求k的值和直线的表达式.
22.如图,已知一次函数y1=kx+b的图像与函数y2=(x>0)的图像交于A(6,-),B(,n)两点,与y轴交于点C,将直线AB沿y轴向上平移t个单位长度得到直线DE,DE与y轴交于点F.
(1) 求y1与y2的解析式;
(2) 观察图像,直接写出y1<y2时x的取值范围;
(3) 连接AD,CD,若△ACD的面积为6,则t的值为 .
23.如图,点P为x轴负半轴上的一个点,过点P作x轴的垂线,交函数的图像于点A,交函数的图像于点B,过点B作x轴的平行线,交于点C,连接AC.
(1)当点P的坐标为(﹣1,0)时,求△ABC的面积;
(2)若AB=BC,求点A的坐标;
(3)连接OA和OC.当点P的坐标为(t,0)时,△OAC的面积是否随t的值的变化而变化?请说明理由.
24.如图 1,木匠陈师傅现有一块五边形木板,它是矩形木板用去后的余料,,,,是边上一点.陈师傅打算利用该余料截取一块矩形材料,其中一条边在上.
[初步探究]
当时.
①若截取的矩形有一边是,则截取的矩形面积的最大值是______;
②若截取的矩形有一边是,则截取的矩形面积的最大值是______;
[问题解决]
如图2,陈师傅还有另一块余料,,,,,,且和之间的距离为4,若以所在直线为轴,中点为原点构建直角坐标系,则曲线是反比例函数图象的一部分,陈师傅想利用该余料截取一块矩形材料,其中一条边在上,所截矩形材料面积是.求的长.
答案
一、单选题
1.B 2.C 3.B 4.A 5.C 6.C 7.B 8.B 9.B 10.C
二、填空题
11.
12.m<0
13.﹣1<k<1
14.二、四
15.2
16.
17.
18.3
三、解答题
19.
解:(1)由题意:联立直线方程,可得,故A点坐标为(-2,4)
将A(-2,4)代入反比例函数表达式,有,∴
故反比例函数的表达式为
(2)联立直线与反比例函数,
解得,当时,,故B(-8,1)
如图,过A,B两点分别作轴的垂线,交轴于M、N两点,由模型可知
S梯形AMNB=S△AOB,
∴S梯形AMNB=S△AOB===
20.
(1)解:∵一次函数y=x+2的图象过点A(1,m),
∴m=1+2=3,
∴A(1,3),
∵点A在反比例函数(x>0)的图象上,
∴k=1×3=3,
∴反比例函数的解析式为;
(2)∵点B是反比例函数图象上一点且纵坐标是1,
∴B(3,1),
作BDx轴,交直线AC于点D,则D点的纵坐标为1,
代入y=x+2得,1=x+2,解得x= 1,
∴D( 1,1),
∴BD=3+1=4,
∴.
21.
解:(1)∵点B在y轴上,,
∴B(0,2),
∵点D落在x轴正半轴上,且
∴D(1,0),
∴线段AB向下平移2个单位,再向右平移1个单位,得到线段CD,
∵点A(m,4),
∴C(m+1,2),
故答案为:(0,2),(1,0),(m+1,2);
(2)∵点A和点C在反比例函数的图象上,
∴k=4m=2(m+1),
∴m=1,
∴A(1,4),C(2,2),
∴k=1×4=4,
设直线AC的表达式为:,
∴ 解得,
∴直线AC的表达式为:y=-2x+6.
22.
解:(1)∵一次函数y1=kx+b的图像与函数y2=(x>0)的图像交于A(6,-),B(,n)两点,
∴, ,
解得:, ,
∴y1、y2的解析式为:,;
(2)从图像上可以看出,当x在AB两点之间时,y1∴x的取值范围为:;
作CG⊥DE于G,如图,
∵直线DE是直线AB沿y轴向上平移t个单位长度得到,
∴,CF=t,
∵直线AB的解析式为,
∴直线AB与y轴的交点为C,与x轴的交点为,
即直线AB与x、y坐标轴的交点到原点O的距离相等,
∴∠FCA=45°,
∵CG⊥DE, ,
∴CG⊥AC,CG等于平行线AB、DE之间的距离,
∴∠GCF=∠GFC=45°,
∴CG==,
∵A、C两点坐标为:A(6,-),C,
∴线段AC=,
∴,
∵△ACD的面积为6,
∴3t=6,
解得:t=2.
23.解:(1)点P( 1,0),则点A( 1,1),点B( 1,4),点C( ,4),
∴S△ABC=BC×AB=×( +1)×(4 1)=;
(2)设点P(t,0),则点A、B、C的坐标分别为(t, )、(t,)、(,),
∵AB=BC,
∴-()= t,解得:t=±2(舍去2),
∴点A( 2,);
(3)过点A作AM⊥y轴于点M,过点C作CN⊥y轴于点N,
则点A、B、C的坐标分别为(t, )、(t,)、(,),
∴S△OAC=S梯形AMNC=( t)(+)=,
∴△OAC的面积不随t的值的变化而变化.
24.
(1)解:①当为矩形一条边,为矩形另一条边时,截取的矩形面积的最大,
,,
,
截取的矩形面积的最大值4;
故答案为:4;
②当为矩形一条边,为矩形另一条边时,截取的矩形面积的最大,
,,
,
截取的矩形面积的最大值10;
故答案为:10;
(2)解:,
,,
,
,,
点在函数图象上,
,
反比例函数的解析式为,
和之间的距离为4,,
,
,
,
设直线的解析式为,
,
解得,
,
设,则,
,
解得,
的长为.
一、单选题
1.如图,点A是反比例函数图象上一点,则下列各点在该函数图象上的是( )
A. B. C. D.
2.运用你学习函数的经验,判断以下哪个函数的图像如图所示( )
A. B. C. D.
3.如图,函数与在同一平面直角坐标系中的大致图象是( )
A. B. C. D.
4.反比例函数(m为常数)的图象在第二、四象限,那么m的取值范围是( )
A. B. C. D.
5.若反比例函数的图象经过点,则它的图象也一定经过的点是( )
A. B. C. D.
6.若点,,在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
7.已知反比例函数y=的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( ).
A.(-1,2) B.(-2,) C.(-2,3) D.(1,-2)
8.如图所示,直线y=-x与双曲线y=交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,k的值为( )
A.-10 B.-9 C.-6 D.-4
9.如图,在平面直角坐标系中,的顶点在轴正半轴上,是的中线,点、在反比例函数的图象上,则的面积等于( )
A.2 B.3 C.4 D.6
10.如图,在以为原点的直角坐标系中,矩形的两边、分别在轴、轴的正半轴上,反比例函数的图像与相交于点,与相交于点,若,且的面积是,则( )
A. B. C. D.
二、填空题
11.已知正比例函数与反比例函数的图象交于点和点,则点的坐标为________.
12.若反比例函数y=(m≠0)与正比例函数y=7x无交点,则m的取值范围是___________
13.设A(x1,y1),B(x2,y2)为函数图象上的两点,且x1<0<x2,y1>y2,则实数k的取值范围是__.
14.如果反比例函数(k是常数,且)的图象经过点,那么这个反比例函数的图象在第______象限.
15.已知函数,,当时,函数的最大值为,函数的最小值为,则的值为______.
16.反比例函数的图像经过点(3,1)、(,2)、(,3),比较大小:________.
17.如图所示,在平面直角坐标系中,等腰直角三角形的顶点、分别在轴、轴的正半轴上,,轴于点,点在函数的图象上,若,则的值为___.
18.如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若,则________.
三、解答题
19.如图,在平面直角坐标系中,一次函数和的图象相交于点,反比例函数的图象经过点.
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为,连接,求的面积.
20.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点,与轴交于点.
求点的坐标和反比例函数的解析式;
点是反比例函数图象上一点且纵坐标是1,连接,,求的面积.
21.如图,点在反比例函数的图象上,点B在y轴上,,将线段向右下方平移,得到线段,此时点C落在反比例函数的图象上,点D落在x轴正半轴上,且.
点B的坐标为__________,点D的坐标为__________,点C的坐标为__________(用含m的式子表示);
求k的值和直线的表达式.
22.如图,已知一次函数y1=kx+b的图像与函数y2=(x>0)的图像交于A(6,-),B(,n)两点,与y轴交于点C,将直线AB沿y轴向上平移t个单位长度得到直线DE,DE与y轴交于点F.
(1) 求y1与y2的解析式;
(2) 观察图像,直接写出y1<y2时x的取值范围;
(3) 连接AD,CD,若△ACD的面积为6,则t的值为 .
23.如图,点P为x轴负半轴上的一个点,过点P作x轴的垂线,交函数的图像于点A,交函数的图像于点B,过点B作x轴的平行线,交于点C,连接AC.
(1)当点P的坐标为(﹣1,0)时,求△ABC的面积;
(2)若AB=BC,求点A的坐标;
(3)连接OA和OC.当点P的坐标为(t,0)时,△OAC的面积是否随t的值的变化而变化?请说明理由.
24.如图 1,木匠陈师傅现有一块五边形木板,它是矩形木板用去后的余料,,,,是边上一点.陈师傅打算利用该余料截取一块矩形材料,其中一条边在上.
[初步探究]
当时.
①若截取的矩形有一边是,则截取的矩形面积的最大值是______;
②若截取的矩形有一边是,则截取的矩形面积的最大值是______;
[问题解决]
如图2,陈师傅还有另一块余料,,,,,,且和之间的距离为4,若以所在直线为轴,中点为原点构建直角坐标系,则曲线是反比例函数图象的一部分,陈师傅想利用该余料截取一块矩形材料,其中一条边在上,所截矩形材料面积是.求的长.
答案
一、单选题
1.B 2.C 3.B 4.A 5.C 6.C 7.B 8.B 9.B 10.C
二、填空题
11.
12.m<0
13.﹣1<k<1
14.二、四
15.2
16.
17.
18.3
三、解答题
19.
解:(1)由题意:联立直线方程,可得,故A点坐标为(-2,4)
将A(-2,4)代入反比例函数表达式,有,∴
故反比例函数的表达式为
(2)联立直线与反比例函数,
解得,当时,,故B(-8,1)
如图,过A,B两点分别作轴的垂线,交轴于M、N两点,由模型可知
S梯形AMNB=S△AOB,
∴S梯形AMNB=S△AOB===
20.
(1)解:∵一次函数y=x+2的图象过点A(1,m),
∴m=1+2=3,
∴A(1,3),
∵点A在反比例函数(x>0)的图象上,
∴k=1×3=3,
∴反比例函数的解析式为;
(2)∵点B是反比例函数图象上一点且纵坐标是1,
∴B(3,1),
作BDx轴,交直线AC于点D,则D点的纵坐标为1,
代入y=x+2得,1=x+2,解得x= 1,
∴D( 1,1),
∴BD=3+1=4,
∴.
21.
解:(1)∵点B在y轴上,,
∴B(0,2),
∵点D落在x轴正半轴上,且
∴D(1,0),
∴线段AB向下平移2个单位,再向右平移1个单位,得到线段CD,
∵点A(m,4),
∴C(m+1,2),
故答案为:(0,2),(1,0),(m+1,2);
(2)∵点A和点C在反比例函数的图象上,
∴k=4m=2(m+1),
∴m=1,
∴A(1,4),C(2,2),
∴k=1×4=4,
设直线AC的表达式为:,
∴ 解得,
∴直线AC的表达式为:y=-2x+6.
22.
解:(1)∵一次函数y1=kx+b的图像与函数y2=(x>0)的图像交于A(6,-),B(,n)两点,
∴, ,
解得:, ,
∴y1、y2的解析式为:,;
(2)从图像上可以看出,当x在AB两点之间时,y1
作CG⊥DE于G,如图,
∵直线DE是直线AB沿y轴向上平移t个单位长度得到,
∴,CF=t,
∵直线AB的解析式为,
∴直线AB与y轴的交点为C,与x轴的交点为,
即直线AB与x、y坐标轴的交点到原点O的距离相等,
∴∠FCA=45°,
∵CG⊥DE, ,
∴CG⊥AC,CG等于平行线AB、DE之间的距离,
∴∠GCF=∠GFC=45°,
∴CG==,
∵A、C两点坐标为:A(6,-),C,
∴线段AC=,
∴,
∵△ACD的面积为6,
∴3t=6,
解得:t=2.
23.解:(1)点P( 1,0),则点A( 1,1),点B( 1,4),点C( ,4),
∴S△ABC=BC×AB=×( +1)×(4 1)=;
(2)设点P(t,0),则点A、B、C的坐标分别为(t, )、(t,)、(,),
∵AB=BC,
∴-()= t,解得:t=±2(舍去2),
∴点A( 2,);
(3)过点A作AM⊥y轴于点M,过点C作CN⊥y轴于点N,
则点A、B、C的坐标分别为(t, )、(t,)、(,),
∴S△OAC=S梯形AMNC=( t)(+)=,
∴△OAC的面积不随t的值的变化而变化.
24.
(1)解:①当为矩形一条边,为矩形另一条边时,截取的矩形面积的最大,
,,
,
截取的矩形面积的最大值4;
故答案为:4;
②当为矩形一条边,为矩形另一条边时,截取的矩形面积的最大,
,,
,
截取的矩形面积的最大值10;
故答案为:10;
(2)解:,
,,
,
,,
点在函数图象上,
,
反比例函数的解析式为,
和之间的距离为4,,
,
,
,
设直线的解析式为,
,
解得,
,
设,则,
,
解得,
的长为.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
