浙教版八年级数学 下册试题第4章 平行四边形--存在性问题(含答案)
文档属性
| 名称 | 浙教版八年级数学 下册试题第4章 平行四边形--存在性问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 08:45:03 | ||
图片预览



文档简介
平行四边形--存在性问题
一、解答题
1.如图,AC是平行四边形ABCD的对角线.
(1)尺规作图:作线段AC的垂直平分线l(不写作法,保留作图痕迹);
(2)直线l分别交AB,AC,CD于点E,F,G.猜想DG与BE存在的数量关系,并证明你猜想的结论.
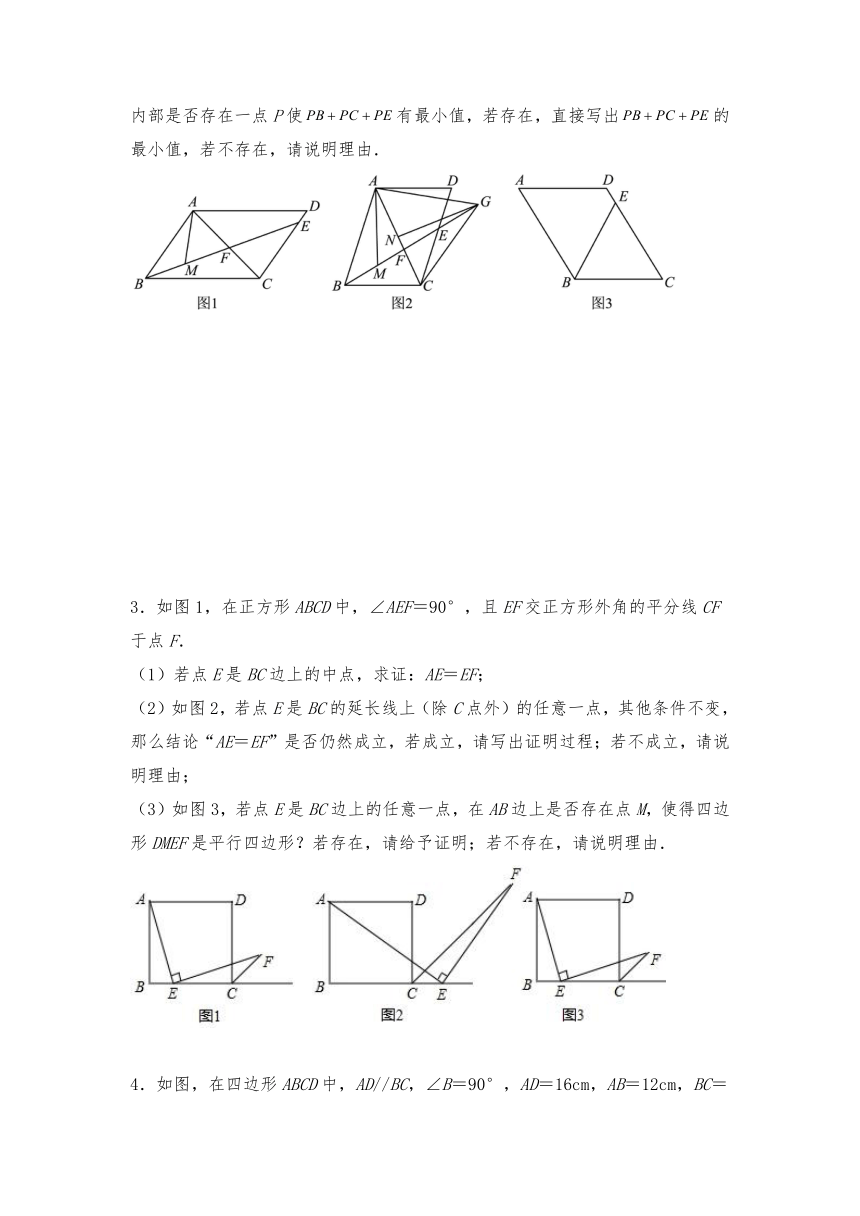
2.如图1,在平行四边形ABCD中,E为边CD上一动点,连接BE交对角线AC于点F,点M为线段BF上一点,连接AM.
(1)如图1,若对角线AC⊥AB,点M是BF的中点,,,求BC的长;
(2)如图2,若,,AC的垂直平分线交BE的延长线于点G,连接AG,CG,AM平分∠BAC交BE于点M,求证:;
(3)如图3,当点E在运动过程中满足BCE为等边三角形时,若;在BCE内部是否存在一点P使有最小值,若存在,直接写出的最小值,若不存在,请说明理由.
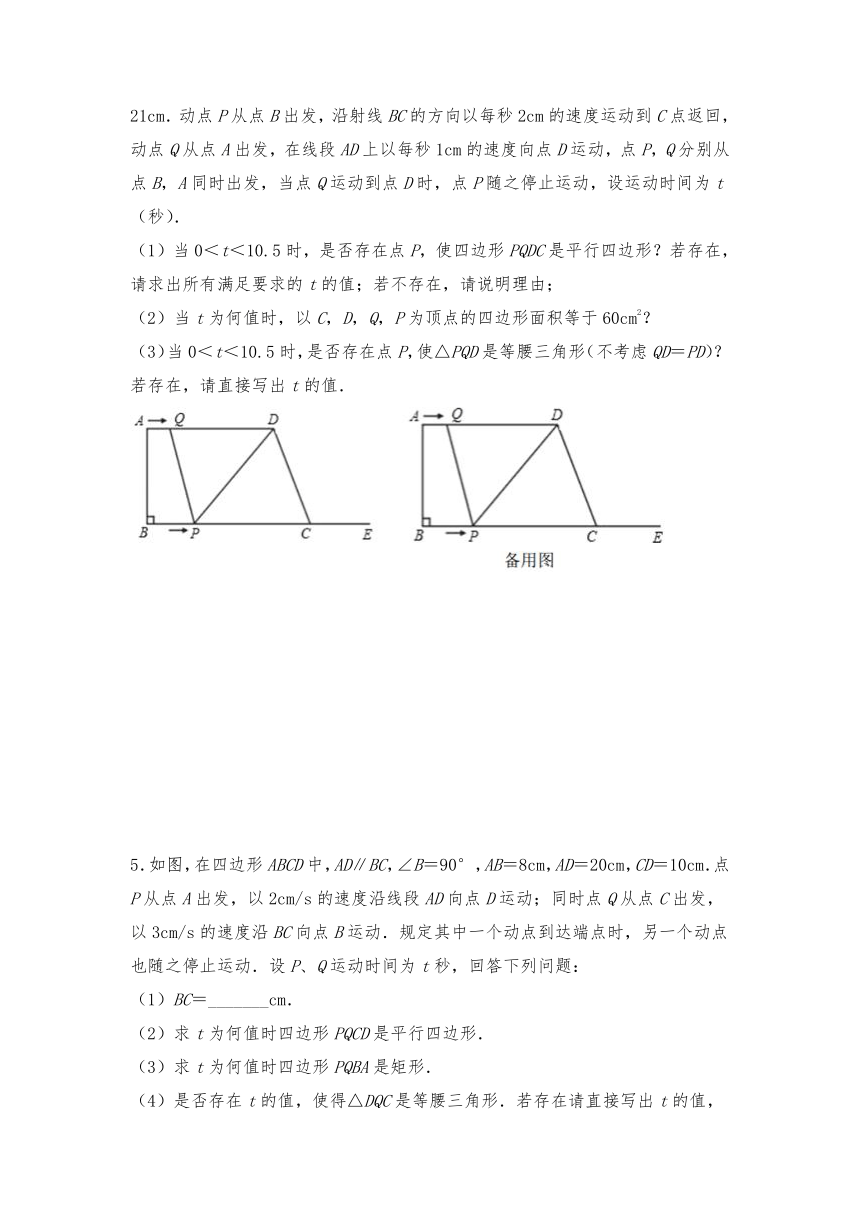
3.如图1,在正方形ABCD中,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)若点E是BC边上的中点,求证:AE=EF;
(2)如图2,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变,那么结论“AE=EF”是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由;
(3)如图3,若点E是BC边上的任意一点,在AB边上是否存在点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.
4.如图,在四边形ABCD中,AD//BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm.动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当0<t<10.5时,是否存在点P,使四边形PQDC是平行四边形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由;
(2)当t为何值时,以C,D,Q,P为顶点的四边形面积等于60cm2?
(3)当0<t<10.5时,是否存在点P,使△PQD是等腰三角形(不考虑QD=PD)?若存在,请直接写出t的值.
5.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=20cm,CD=10cm.点P从点A出发,以2cm/s的速度沿线段AD向点D运动;同时点Q从点C出发,以3cm/s的速度沿BC向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设P、Q运动时间为t秒,回答下列问题:
(1)BC=_______cm.
(2)求t为何值时四边形PQCD是平行四边形.
(3)求t为何值时四边形PQBA是矩形.
(4)是否存在t的值,使得△DQC是等腰三角形.若存在请直接写出t的值,若不存在,请说明理由.
6.如图,在四边形ABCD中,,,,,.
(1)求AB的长;
(2)动点P从点B出发,沿射线BC以每秒2个单位长度的速度运动,同时动点Q从点A出发,沿线段AD以每秒1个单位长度的速度运动,当点Q运动到点D时,两点同时停止运动,设运动的时间为t秒.
①当t为何值时,以P、Q、D、C为顶点的四边形为平行四边形?
②是否存在点P,使是以PQ为腰的等腰三角形?若存在,请直接写出相应的t的值;若不存在,请说明理由.
7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
(1)当t为何值时,四边形PQDC是平行四边形;
(2)当t为何值时,以C,D,Q,P为顶点的四边形面积等于60cm2?
(3)当08.如图,在等边三角形ABC中,边长为12cm,点P从点A出发,沿AC方向匀速运动,速度是3cm/s;同时点Q由B点出发,沿BA方向匀速运动,速度为1cm/s,过点Q的直线QE∥AC,交BC于点E,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,PQ⊥AC?
(2)当点P在线段AD上时,设四边形PQEC的面积为ycm2,求y与t的关系式;
(3)在整个运动过程中,是否存在某一时刻t,使得以P,Q,E,D为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,求出t的值,若不存在,说明理由
9.如图,中,,,点是边上一动点,以的速度由向运动,同时点从点出发,在延长线上,以的速度向左运动,运动时间为秒,当点到达点时,两点停止运动.连接交于点,过点作于,过点作的垂线交延长线于,连接.
(1)用含的代数式表示线段长度:________,________;
(2)当取何值时,四边形是平行四边形?请写出推理过程.
(3)在运动过程中,点是否总是的中点?请说明理由.
(4)是否存在某一时刻,使得是等腰三角形?若存在,求出的值;若不存在,请说明理由.
10.在学习完了《平行四边形的性质》之后,王老师在数学活动课上对下面一个问题让学生展开探究活动.
问题情境:图1,在 ABCD中,CA⊥AB,AB=6cm,AC=8cm,点O为AC的中点,动点P在BC边上运动,直线PO交AD于E.
问题发现:数学智慧小组”通过积极的动手操作,观察,猜想,提出了如下问题:
(1)在点P运动的过程中,始终存在PO=OE,为什么?
(2)在点P运动到PO⊥AC时,四边形ABPE是平行四边形,为什么?此时BP的长度是多少?
(3)在点P运动的过程中,四边形ABPE的周长是否存在最小值?如果存在,则四边形ABPE的周长的最小值是 cm;BP的长度为 cm.
问题解决:
“数学智慧小组”欢迎您的加入,请开启您的“问题解决之旅”吧!
11.如图,矩形OABC在平面直角坐标系中,OB,OC是x2﹣12x+32=0的两根,OC>OA,
(1)求B点的坐标.
(2)把ABC沿AC对折,点B落在点处,线段与x轴交于点D,在平面上是否存在点P,使D、C、B、P四点形成的四边形为平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
12.如图,在平行四边形中,,..点在上由点向点出发,速度为每秒;点在边上,同时由点向点运动,速度为每秒.当点运动到点时,点,同时停止运动.连接,设运动时间为秒.
(1)当为何值时,四边形为平行四边形?
(2)设四边形的面积为,求与之间的函数关系式.
(3)当为何值时,四边形的面积是四边形的面积的四分之三?求出此时的度数.
(4)连接,是否存在某一时刻,使为等腰三角形?若存在,请求出此刻的值;若不存在,请说明理由.
13.如图,在中,,,,点从点出发沿方向以/秒的速度向点匀速运动,同时点从点出发沿方向以/秒的速度向点匀速运动,设点、运动的时间是秒(),过点作于点,连接、.
(1)求证:四边形是平行四边形;
(2)当为何值时,动点恰好在的垂直平分线上;
(3)点、在运动过程中是否存在的值,使是直角三角形,若存在求出的值,若不存在,说明理由.
14.如图,在平面直角坐标系xOy中,直线与x轴,y轴分别交于点A,B,点C的坐标是.
(1)求的度数;
(2)若第一象限内存在点D,使四边形ABCD是平行四边形,求点D的坐标.
15.综合与探究
如图,平行四边形ABCD在平面直角坐标系中,点B在x轴负半轴上,点D在第一象限,A,C两点的坐标分别为(0,4),(3,0),边AD的长为6.
(1)点B的坐标为 ;
(2)若E为x轴正半轴上的点,且S△AOE =,求经过D,E两点的直线的解析式;
(3)若点N在平面直角坐标系内,则在x轴上是否存在点F使以A,C,F,N为顶点的四边形为菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
16.如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,连接CD,∠ADC=120°,把△ADC绕点A逆时针旋转得到(旋转后点C、D的对应点分别为、),设旋转的度数为m(0°≤m≤360°).
(1)当m=30°时,如图2,连接C并延长,交AB于点E.请直接写出∠AC的度数;
(2)在(1)的条件下,请判断△DCE的形状,并说明理由;
(3)①小明在探究的过程中发现:当m=90°时,如图3,四边形ACB为平行四边形,请证明小明的结论的正确性;
②请你再探究:在△ADC绕点A逆时针旋转过程中,是否存在其他的情形,使以A、B、C、四点组成的四边形为平行四边形?若存在,请在备用图中画出旋转后的图形,并请直接写出m的值;若不能,请说明理由.
17.问题探究:
(1)如图1,平行四边形ABCD,∠ABC=60°,AB=3,BC=5,M、N分别为AD、DC上的点,且DM+DN=4,则四边形BMDN的面积最大值是 .
(2)如图2,∠ACB=90°,且AC+BC=4,连接AB,则△ABC的周长是否存在最小值?若存在,求出最小值;若不存在,说明理由.
问题解决
(3)如图3,在四边形ABCD中,AD∥BC,对角线AC交BD于O,已知∠AOB=120°,且AC+BD=10,则△AOD与△BOC的周长之和是否为定值?若是,求出定值;若不是,求出最小值.
答案
一、解答题
1.
(1) 解:如图,直线l为所作;
解:DG=BE,理由如下:
证明:标注如图字母,
∵EG垂直平分AC,
∴FA=FC,
∵四边形ABCD为平行四边形,
∴CD∥AB,CD=AB,
∴∠DCA=∠BAC,
在△CFG和△AFE中,
,
∴△CFG≌△AFE(ASA),
∴CG=AE,
∴CD-CG=AB-AE,
即DG=BE.
2.
解:∵AC⊥AB,
∴∠BAC=90°;
∵点M为BF的中点,
∴,
∴BF=6,
∴
∵,
∴
∵在Rt△ABC中,∠BAC=90°
∴
解:连接并延长MC,过点C作CQ⊥BC交BE于点Q,
分别过点G作GH⊥MC于点H,作GP⊥AM于点P.
∵,AM平分∠BAC,
∴△ABM≌△ACM(SAS);
∴,∠AMB=∠AMC,
∵∠CBE=30°,BM=MC,
∴∠BCM=∠CBE=30°,
∴∠CMQ=∠BCM+∠CBE=60°,∠BMC=120°,
∴∠AMB=∠AMC=120°,
∴∠AMG=∠CMG=60°.
∵CQ⊥BC,∠MCB=30°,
∴∠MCQ=∠BCQ-∠BCM=60°.
∴∠MQC=∠MCQ=∠CMQ=60°.
∴.
∴.
∵GH⊥MC,GP⊥AM,∠AMG=∠CMG.
∴∠MPG=∠MHG=90°,.
∴,
∵点G在AC的垂直平分线上,
∴.
在Rt△AGP与Rt△CGH中,
,
∴△AGP≌OCGH(HL)
∴∠AGP=∠CGH,
∴∠AGC=∠PGH=60°,
∴△AGC为等边三角形,
∴,∠ACM=∠GCQ.
在△ACM与△GCQ中,
,
∴△ACM≌△GCQ(SAS),
∴.
∵,
∴.
解:存在,的最小值为.
取任意点P,连接PB、PC、PE,以BP为边作等边三角形BPP1,作点E关于BC的对称点C1,连接B C1,C C1,当点E、P、P1、C1四点共线时,有最小值,
连接BP、CC1相交于点Q,连接EQ,
∵△BPP1是等边三角形,
∴∠PBP1=60°,
由轴对称可得∠EBP=∠C1BP1=30°,∠BC1C=60°,△BCC1是等边三角形,
∴∠C1BQ=90°,∠BQC=30°,
∴C1Q=2BC1=2BC=8,
∴CQ=BC=4=CE,
∵∠ECQ=60°,
∴△ECQ是等边三角形,
∴∠EQB=∠CQB=30°,
∵点E、P、P1、C1四点共线,
∴C1E垂直平分BC,
∴∠ECP=∠EBP= =30°,
∴∠PCQ=90°,
同理∠PEQ=90°,
∴PQ=2PC=2PE,
∴PQ=PC+PE,
∴BQ=PB+PC+PE,
∵,
∴的最小值为.
3.
(1)证明:在BA上截取BG=BE,连结GE,
∵四边形ABCD为正方形,
∴AB=BC,∠B=90°,∠BCD=90°,
∵BG=BE,
∴AB-BG=BC-BE,即AG=EC,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∵AE⊥EF,
∴∠AEF=90°,
∴∠1+∠BEA=∠BEA+∠2=90°,
∴∠1=∠2,
∵CF平分∠DCB的外角,
∴∠DCF=45°,
∴∠ECF=∠ECD+∠DCF=90°+45°=135°,
∴∠AGE=∠ECF,
在△AGE和△ECF中,
∴△AGE≌△ECF(ASA),
∴AE=EF;
(2)AE=EF应然成立
证明:∵四边形ABCD为正方形,
∴AB=BC,∠ABE=90°,
延长BA到G,使BG=BE,
∴BG-AB=BE-BC,即GA=CE,∠AGE=45°,
∵AE⊥EF,
∴∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
∴180°-∠BAE=180°-∠HEF即∠GAE=∠CEF,
∵CF平分∠HCB的外角,
∴∠ECF=45°,
∴∠AGE=∠ECF,
在△AGE和△ECF中,
∴△AGE≌△ECF(ASA),
∴AE=EF;
(3)存在,理由如下,
证明:在AB上截取AM=BE,AE与MD交于N,
∵四边形ABCD为正方形,
∴∠DAM=∠ABE=90°,AD=AB,
在△ABE和△DAM中,
∴△ABE≌△DAM(SAS),
∴AE=DM,∠ADM=∠BAE,
∵∠AMD+∠ADM=∠BAE+∠AMD=90°,即∠AMN+∠MAN=90°,
∴∠ANM=180°-90°=90°,
∴AE⊥MD,
∵AE⊥EF,
∴MD∥EF,
∵△AGE≌△ECF,
∴AE=EF,
∴DM=EF,
∵MDEF,且MD=EF,
∴四边形DMEF是平行四边形.
4.
解:(1)四边形是平行四边形,
,
当从运动到时,
,
解得
当秒时,四边形是平行四边形;
(2)若点、分别沿、运动时,
,
即,
解得(秒
若点返回时,,
则
解得(秒.
故当或15秒时,以,,,为顶点的梯形面积等;
(3)当时
作于,则,
,
秒;
当时,,,
解得(秒,
综上可知,当秒或秒时,是等腰三角形.
5.
解:(1)过D作DH⊥BC于H,如图:
∵AD∥BC,∠B=90°,DH⊥BC,
∴四边形ABHD是矩形,
∴DH=AB=8,BH=AD=20,
在Rt△DHC中,CH===6,
∴BC=BH+CH=20+6=26(cm),
故答案为:26;
(2)如图:
根据题意可得:AP=2t,CQ=3t,
∵AD∥BC,
∴四边形PQCD是平行四边形,只需PD=CQ,即20﹣2t=3t,
解得t=4,
(3)如图:
∵AD∥BC,∠B=90°,
∴四边形PQBA是矩形,只需AP=BQ,即2t=26﹣3t,
解得t=5.2;
(4)存在,理由如下:
①若CD=DQ,过D作DH⊥BC于H,如图:
由(1)可知:CH=6,
∵CD=DQ,DH⊥BC,
∴CQ=2CH=12,
∴3t=12,
∴t=4,
②若CD=CQ,如图:
∴3t=10,
∴t=,
③若DQ=CQ,过D作DH⊥BC于H,如图:
在Rt△DQH中,QH=CQ﹣CH=3t﹣6,DH=8,DQ=CQ=3t,
由勾股定理得:(3t﹣6)2+82=(3t)2,
∴t=,
综上所述,△DQC是等腰三角形,t的值为:4或或.
6.
解:(1)如图1,过点D作于点E,则四边形ABED为矩形,
∴,,
∵,,,
∴,
由勾股定理得:,
∴;
(2)①如图2,
∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,且P在BC上,
∵DQ=AD-AQ=16-t,CP=21-2t,
∴16-t=21-2t,
解得:t=5,
∴当t=5秒时,四边形PQDC是平行四边形;
当点P在BC延长线上时,
∴16-t=2t-21,
解得:t=,
∴t=5秒或秒时,P、Q、D、C为顶点的四边形为平行四边形;
②当PQ=PD时,
如图3,作PH⊥AD于H,则HQ=HD,
∵QH=HD=QD=(16-t),
∵AH=BP,
∴2t=(16-t)+t,
∴t= ;
当PQ=QD时,QH=AH-AQ=BP-AQ=2t-t=t,QD=16-t,
∵QD2=PQ2=t2+122,
∴(16-t)2=122+t2,
解得:t=.
综上可知,当t=秒或秒时,△PQD是等腰三角形.
7.
解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,
∵DQ=AD﹣AQ=16﹣t,
CP=21﹣2t,
∴16﹣t=21﹣2t,
解得:t=5,
当P从C运动到B时,
∵DQ=AD﹣AQ=16﹣t,
CP=2t﹣21,
∴16﹣t=2t﹣21,
解得:t=,
∴当t=5或秒时,四边形PQDC是平行四边形;
(2)若点P、Q分别沿AD、BC运动时,
(DQ+CP) AB=60,
即(16﹣t+21﹣2t)×12=60,
解得:t=9(秒),
若点P返回时,CP=2t﹣2,
则(16﹣t+2t﹣21))×12=60,
解得:t=15(秒).
故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;
(3)当PQ=PD时,作PH⊥AD于H,则HQ=HD,
∵QH=HD=QD=(16﹣t),
∵AH=BP,
∴2t=(16﹣t)+t,
∴t=秒;
当PQ=QD时,QH=AH﹣AQ=BP﹣AQ=2t﹣t=t,QD=16﹣t,
∵QD2=PQ2=t2+122,
∴(16﹣t)2=122+t2,
解得t=(秒);
当QD=PD时,DH=AD﹣AH=AD﹣BP=16﹣2t,
∵QD2=PD2=PH2+HD2=122+(16﹣2t)2,
∴(16﹣t)2=122+(16﹣2t)2,
即3t2﹣32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=秒或秒时,△PQD是等腰三角形.
8.
解:(1)是等边三角形,
,
,
,
,
,
由题意得:,,则,
,
解得:,
当为时,;
(2)过点作于,过点作于,如图1所示:
,
是等边三角形,
,
,
,,
,,
在中,由勾股定理得:,
在中,由勾股定理得:,
,
,
,
,
是等边三角形,
,
,
,
,
在中,由勾股定理得:,
,
,
当点在线段上时,与的关系式为:;
(3)存在,理由如下:
①当四边形是平行四边形时,如图2所示:
则,
,
,
,
是等边三角形,
,
,
,
,
;
②当四边形是平行四边形时,如图3所示:
则,
同①得:是等边三角形,
,
,
,
,
;
综上所述,当为或时,使得以,,,为顶点的四边形是平行四边形.
9.
(1),,
,
,
是等腰
是等腰
.
(2),
当时,四边形是平行四边形
是等腰
,
解得:.
当时,四边形是平行四边形
(3)如图:过作,连接,
又
是等腰
,
.
四边形是平行四边形
点为对角线的交点
即总是的中点.
(4)由(3)四边形是平行四边形
是等腰三角形
所以为顶角
,
.
,
解得:.
当,使得是等腰三角形.
10.
(1)证明:∵四边形ABCD是平行四边形,点O为AC的中点,
∴AE∥PC,AO=OC,
∴∠EAO=∠PCO,∠AOE=∠COP,
∴△AEO△CPO,
∴PO=OE;
(2)∵CA⊥AB,且PO⊥AC,
∴PO∥AB,即EP∥AB,
∵四边形ABCD是平行四边形,
∴AE∥BP,
∵CA⊥AB,且AB=6cm,AC=8cm,
∴BC=(cm),
∴四边形ABPE是平行四边形,
∵点O为AC的中点,且PO∥AB,
∴BP=PC=BC=5(cm);
(3)四边形ABPE的周长为:AB+BP+PE+AE,
由(1)知△AEO△CPO,则AE=CP,
∴BP+AE=BP+CP=BC=10,
∴四边形ABPE的周长为:6+10+PE=16+PE,
则PE最小时,四边形ABPE的周长最小,
∴当PE⊥BC时,PE最小(垂线段最短),
∵BCPE=ABAC,
∴PE=(cm),
∴四边形ABPE的周长最小值为16+=(cm),
∵△AEO△CPO,
∴PO=EO=PE=(cm),OC=AC=(cm),
∴PC=(cm),
∴BP=BC-PC=(cm),
故答案为:,.
.
11.
(1)x2﹣12x+32=0,
解得x1=4,x2=8,
∵OC>OA,
∴OA=4,OC=8,
故B点坐标为(8,4)
(2)由对折可知,∠DAC=∠BAC,
又∵四边形OABC为矩形,
∴AB//OC,∠BAC=∠ACO
∴∠DAC=∠ACO,
∴AD=CD,
设AD=x,则OD=8-x,
在中,满足有
化简得
解得x=5,
故OD=8-5=3
故D点坐标为(3,0)
由平行四边形性质可知P1(3,4),P2(13,4),P3(3,-4)时D、C、B、P四点形成的四边形为平行四边形.
12.
解:(1)∵在平行四边形中,,,
由运动知,AQ=16 t,BP=2t,
∵四边形ABPQ为平行四边形,
∴AQ=BP,
∴16 t=2t
∴t=,
即:t=s时,四边形ABPQ是平行四边形;
(2)过点A作AE⊥BC于E,如图,
在Rt△ABE中,∠B=30°,AB=8,
∴AE=4,
由运动知,BP=2t,DQ=t,
∵四边形ABCD是平行四边形,
∴AD=BC=16,
∴AQ=16 t,
∴y=S四边形ABPQ=(BP+AQ) AE=(2t+16 t)×4=2t+32(0<t≤8);
(3)由(2)知,AE=4,
∵BC=16,
∴S四边形ABCD=16×4=64,
由(2)知,y=S四边形ABPQ=2t+32(0<t≤8),
∵四边形ABPQ的面积是四边形ABCD的面积的四分之三
∴2t+32=×64,
∴t=8;
如图,
当t=8时,点P和点C重合,DQ=8,
∵CD=AB=8,
∴DP=DQ,
∴∠DQC=∠DPQ,
∴∠D=∠B=30°,
∴∠DQP=75°;
(4)①当AB=BP时,BP=8,
即2t=8,t=4;
②当AP=BP时,如图,
∵∠B=30°,
过P作PM垂直于AB,垂足为点M,
∴BM=4,,
解得:BP=,
∴2t=,
∴t=
③当AB=AP时,同(2)的方法得,BP=,
∴2t=,
∴t=
所以,当t=4或 或时,△ABP为等腰三角形.
13.
(1)证明:根据题意得:AD=4tcm,BE=2tcm,
∵,
∴CD=(60-4t)cm,
∵, ,
∴∠C=30°,
∴ ,
∵,
∴, ,
∴AE=(30-2t)cm,
∴AE=DF,,
∴四边形是平行四边形;
(2)解: 若点恰好在的垂直平分线上,则AD=DF,
∴4t=30-2t,
解得:t=5,
即当为5秒时,动点恰好在的垂直平分线上;
(3)解:存在,理由如下:
如图,当∠FDE=90°时,
∵∠DFC=∠B=∠FDE=90°,
∴四边形BEDF是矩形,
∴DF=BE=2t,DE∥BC,
∴∠ADE=∠C=30°,
∴AD=2AE=60-4t,
又∵AD=4t,
∴4t=60-4t,
解得:;
如图,当∠DEF=90°时,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴∠ADE=∠DEF=90°,
∵∠A=60°,
∴∠AED=30°,
∴AE=2AD,即30-2t=2×4t,
解得:t=3;
综上所述,当t=3或时,是直角三角形.
14.
解:(1)如图,作轴,垂足为点E.
∵直线与x轴,y轴分别交于点A,B,
∴当时,,当时,.
∴点A,B的坐标分别是,.
∴.
∵,
∴.
∵点C的坐标是,
∴,.
∴.
∴
∵,
∴.
∴,
即∠ABC的度数是90°.
(2)如图,四边形ABCD是平行四边形,作轴,垂足为点F.
∴,∠AFD=90°.
∵,
∴四边形ABCD是矩形.
∴.
∵,
∴.
∴.
∵,
∴.
∴,.
∴.
∴点D的坐标是.
15.
解:(1)平行四边形ABCD中,
AD=6
BC=6,
C(3,0),
B(﹣3,0)
故答案为:B(﹣3,0);
(2)∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵OA=4,
∴D(6,4),
∵S△AOE=×4×OE=,
∴OE=,
∴E(,0),
设经过D、E两点的直线解析式为:y=kx+b,
把点D(6,4),E(,0)代入得:,
解得:k=,b=﹣,
∴经过D、E两点的直线解析式为:y=x﹣;
(3)存在;N的坐标为(﹣5,4)或(5,4)或(0,-4)或(,4),理由如下:
分两种情况讨论,
①若以AC为边,CF为边,如图,
当点F在点C的右侧时,
四边形是菱形,
A(0,4),
(5,4)
当点F在点C的左侧时,
四边形是菱形,
A(0,4),
(-5,4);
若以AC为边,CF为对角线,如图,
四边形是菱形,
,且
A(0,4),
(0,-4);
②若以AC为对角线,如图,
此时菱形中,,
在中
(,4)
综上所述,存在点F使以A,C,F,N为顶点的四边形为菱形,N的坐标为(﹣5,4)或(5,4)或(0,-4)或(,4).
16.
解:(1)由旋转知AC=A,
∵∠CA=30°,
∴∠AC==75°;
(2)△DCE是等边三角形,
理由:在Rt△ABC中,∠ACB=90°,AB=AC,
∴∠ABC=∠BAC=45°,
由(1)知,∠AC=75°,
∴∠BCE=90°﹣∠AC=15°,
∴∠AEC=∠ABC+∠BCE=60°,
∵∠ADC+∠CDE=180°,∠ADC=120°,
∴∠CDE=60°,
∴∠CDE=∠DEC=∠ECD=60°,
∴△DCE是等边三角形;
(3)①当m=90°时,四边形ACB为平行四边形,如图3所示:
∵∠ACB=90°,∠BA=90°,
∴∠ACB+∠BA=180°,
∴,
∵A=AC,AC=BC,
∴A=BC,
∴四边形ACB为平行四边形;
②当m=270°时,四边形ACBC′为平行四边形,如图4所示:
当m=270°时,∠AC=90°,
∴∠AC=∠ACB,
∴A=BC,
∵A=CB,
∴四边形ACB为平行四边形,
综上所述,当m=90°或m=270°时,以A、B、C、四点组成的四边形为平行四边形.
17.
解:(1)过点作,交延长线于,过点作,交的延长线于,
四边形是平行四边形,
,,,,
,,
,
,,
,,
四边形的面积,
,
,
∴
四边形的面积
,
四边形的面积,
则当有最小值时,四边形的面积有最大值,
,
,
∵DN≤3,
∴4-DM≤3,
∴DM≥1,
当时,四边形的面积,
故答案为;
(2)存在,
设,
,
,
,
的周长,
当时,的周长的最小值为;
(3)与的周长之和不是定值,
理由如下:如图3,过点作,交的延长线于,过点作于,
,,
四边形是平行四边形,
,,
,
设,则,
,
,
,
,
,
,
,
,
与的周长之和不是定值,
当时,与的周长之和的最小值为15.
一、解答题
1.如图,AC是平行四边形ABCD的对角线.
(1)尺规作图:作线段AC的垂直平分线l(不写作法,保留作图痕迹);
(2)直线l分别交AB,AC,CD于点E,F,G.猜想DG与BE存在的数量关系,并证明你猜想的结论.
2.如图1,在平行四边形ABCD中,E为边CD上一动点,连接BE交对角线AC于点F,点M为线段BF上一点,连接AM.
(1)如图1,若对角线AC⊥AB,点M是BF的中点,,,求BC的长;
(2)如图2,若,,AC的垂直平分线交BE的延长线于点G,连接AG,CG,AM平分∠BAC交BE于点M,求证:;
(3)如图3,当点E在运动过程中满足BCE为等边三角形时,若;在BCE内部是否存在一点P使有最小值,若存在,直接写出的最小值,若不存在,请说明理由.
3.如图1,在正方形ABCD中,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)若点E是BC边上的中点,求证:AE=EF;
(2)如图2,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变,那么结论“AE=EF”是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由;
(3)如图3,若点E是BC边上的任意一点,在AB边上是否存在点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.
4.如图,在四边形ABCD中,AD//BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm.动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当0<t<10.5时,是否存在点P,使四边形PQDC是平行四边形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由;
(2)当t为何值时,以C,D,Q,P为顶点的四边形面积等于60cm2?
(3)当0<t<10.5时,是否存在点P,使△PQD是等腰三角形(不考虑QD=PD)?若存在,请直接写出t的值.
5.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=20cm,CD=10cm.点P从点A出发,以2cm/s的速度沿线段AD向点D运动;同时点Q从点C出发,以3cm/s的速度沿BC向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设P、Q运动时间为t秒,回答下列问题:
(1)BC=_______cm.
(2)求t为何值时四边形PQCD是平行四边形.
(3)求t为何值时四边形PQBA是矩形.
(4)是否存在t的值,使得△DQC是等腰三角形.若存在请直接写出t的值,若不存在,请说明理由.
6.如图,在四边形ABCD中,,,,,.
(1)求AB的长;
(2)动点P从点B出发,沿射线BC以每秒2个单位长度的速度运动,同时动点Q从点A出发,沿线段AD以每秒1个单位长度的速度运动,当点Q运动到点D时,两点同时停止运动,设运动的时间为t秒.
①当t为何值时,以P、Q、D、C为顶点的四边形为平行四边形?
②是否存在点P,使是以PQ为腰的等腰三角形?若存在,请直接写出相应的t的值;若不存在,请说明理由.
7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
(1)当t为何值时,四边形PQDC是平行四边形;
(2)当t为何值时,以C,D,Q,P为顶点的四边形面积等于60cm2?
(3)当0
(1)当t为何值时,PQ⊥AC?
(2)当点P在线段AD上时,设四边形PQEC的面积为ycm2,求y与t的关系式;
(3)在整个运动过程中,是否存在某一时刻t,使得以P,Q,E,D为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,求出t的值,若不存在,说明理由
9.如图,中,,,点是边上一动点,以的速度由向运动,同时点从点出发,在延长线上,以的速度向左运动,运动时间为秒,当点到达点时,两点停止运动.连接交于点,过点作于,过点作的垂线交延长线于,连接.
(1)用含的代数式表示线段长度:________,________;
(2)当取何值时,四边形是平行四边形?请写出推理过程.
(3)在运动过程中,点是否总是的中点?请说明理由.
(4)是否存在某一时刻,使得是等腰三角形?若存在,求出的值;若不存在,请说明理由.
10.在学习完了《平行四边形的性质》之后,王老师在数学活动课上对下面一个问题让学生展开探究活动.
问题情境:图1,在 ABCD中,CA⊥AB,AB=6cm,AC=8cm,点O为AC的中点,动点P在BC边上运动,直线PO交AD于E.
问题发现:数学智慧小组”通过积极的动手操作,观察,猜想,提出了如下问题:
(1)在点P运动的过程中,始终存在PO=OE,为什么?
(2)在点P运动到PO⊥AC时,四边形ABPE是平行四边形,为什么?此时BP的长度是多少?
(3)在点P运动的过程中,四边形ABPE的周长是否存在最小值?如果存在,则四边形ABPE的周长的最小值是 cm;BP的长度为 cm.
问题解决:
“数学智慧小组”欢迎您的加入,请开启您的“问题解决之旅”吧!
11.如图,矩形OABC在平面直角坐标系中,OB,OC是x2﹣12x+32=0的两根,OC>OA,
(1)求B点的坐标.
(2)把ABC沿AC对折,点B落在点处,线段与x轴交于点D,在平面上是否存在点P,使D、C、B、P四点形成的四边形为平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
12.如图,在平行四边形中,,..点在上由点向点出发,速度为每秒;点在边上,同时由点向点运动,速度为每秒.当点运动到点时,点,同时停止运动.连接,设运动时间为秒.
(1)当为何值时,四边形为平行四边形?
(2)设四边形的面积为,求与之间的函数关系式.
(3)当为何值时,四边形的面积是四边形的面积的四分之三?求出此时的度数.
(4)连接,是否存在某一时刻,使为等腰三角形?若存在,请求出此刻的值;若不存在,请说明理由.
13.如图,在中,,,,点从点出发沿方向以/秒的速度向点匀速运动,同时点从点出发沿方向以/秒的速度向点匀速运动,设点、运动的时间是秒(),过点作于点,连接、.
(1)求证:四边形是平行四边形;
(2)当为何值时,动点恰好在的垂直平分线上;
(3)点、在运动过程中是否存在的值,使是直角三角形,若存在求出的值,若不存在,说明理由.
14.如图,在平面直角坐标系xOy中,直线与x轴,y轴分别交于点A,B,点C的坐标是.
(1)求的度数;
(2)若第一象限内存在点D,使四边形ABCD是平行四边形,求点D的坐标.
15.综合与探究
如图,平行四边形ABCD在平面直角坐标系中,点B在x轴负半轴上,点D在第一象限,A,C两点的坐标分别为(0,4),(3,0),边AD的长为6.
(1)点B的坐标为 ;
(2)若E为x轴正半轴上的点,且S△AOE =,求经过D,E两点的直线的解析式;
(3)若点N在平面直角坐标系内,则在x轴上是否存在点F使以A,C,F,N为顶点的四边形为菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
16.如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,连接CD,∠ADC=120°,把△ADC绕点A逆时针旋转得到(旋转后点C、D的对应点分别为、),设旋转的度数为m(0°≤m≤360°).
(1)当m=30°时,如图2,连接C并延长,交AB于点E.请直接写出∠AC的度数;
(2)在(1)的条件下,请判断△DCE的形状,并说明理由;
(3)①小明在探究的过程中发现:当m=90°时,如图3,四边形ACB为平行四边形,请证明小明的结论的正确性;
②请你再探究:在△ADC绕点A逆时针旋转过程中,是否存在其他的情形,使以A、B、C、四点组成的四边形为平行四边形?若存在,请在备用图中画出旋转后的图形,并请直接写出m的值;若不能,请说明理由.
17.问题探究:
(1)如图1,平行四边形ABCD,∠ABC=60°,AB=3,BC=5,M、N分别为AD、DC上的点,且DM+DN=4,则四边形BMDN的面积最大值是 .
(2)如图2,∠ACB=90°,且AC+BC=4,连接AB,则△ABC的周长是否存在最小值?若存在,求出最小值;若不存在,说明理由.
问题解决
(3)如图3,在四边形ABCD中,AD∥BC,对角线AC交BD于O,已知∠AOB=120°,且AC+BD=10,则△AOD与△BOC的周长之和是否为定值?若是,求出定值;若不是,求出最小值.
答案
一、解答题
1.
(1) 解:如图,直线l为所作;
解:DG=BE,理由如下:
证明:标注如图字母,
∵EG垂直平分AC,
∴FA=FC,
∵四边形ABCD为平行四边形,
∴CD∥AB,CD=AB,
∴∠DCA=∠BAC,
在△CFG和△AFE中,
,
∴△CFG≌△AFE(ASA),
∴CG=AE,
∴CD-CG=AB-AE,
即DG=BE.
2.
解:∵AC⊥AB,
∴∠BAC=90°;
∵点M为BF的中点,
∴,
∴BF=6,
∴
∵,
∴
∵在Rt△ABC中,∠BAC=90°
∴
解:连接并延长MC,过点C作CQ⊥BC交BE于点Q,
分别过点G作GH⊥MC于点H,作GP⊥AM于点P.
∵,AM平分∠BAC,
∴△ABM≌△ACM(SAS);
∴,∠AMB=∠AMC,
∵∠CBE=30°,BM=MC,
∴∠BCM=∠CBE=30°,
∴∠CMQ=∠BCM+∠CBE=60°,∠BMC=120°,
∴∠AMB=∠AMC=120°,
∴∠AMG=∠CMG=60°.
∵CQ⊥BC,∠MCB=30°,
∴∠MCQ=∠BCQ-∠BCM=60°.
∴∠MQC=∠MCQ=∠CMQ=60°.
∴.
∴.
∵GH⊥MC,GP⊥AM,∠AMG=∠CMG.
∴∠MPG=∠MHG=90°,.
∴,
∵点G在AC的垂直平分线上,
∴.
在Rt△AGP与Rt△CGH中,
,
∴△AGP≌OCGH(HL)
∴∠AGP=∠CGH,
∴∠AGC=∠PGH=60°,
∴△AGC为等边三角形,
∴,∠ACM=∠GCQ.
在△ACM与△GCQ中,
,
∴△ACM≌△GCQ(SAS),
∴.
∵,
∴.
解:存在,的最小值为.
取任意点P,连接PB、PC、PE,以BP为边作等边三角形BPP1,作点E关于BC的对称点C1,连接B C1,C C1,当点E、P、P1、C1四点共线时,有最小值,
连接BP、CC1相交于点Q,连接EQ,
∵△BPP1是等边三角形,
∴∠PBP1=60°,
由轴对称可得∠EBP=∠C1BP1=30°,∠BC1C=60°,△BCC1是等边三角形,
∴∠C1BQ=90°,∠BQC=30°,
∴C1Q=2BC1=2BC=8,
∴CQ=BC=4=CE,
∵∠ECQ=60°,
∴△ECQ是等边三角形,
∴∠EQB=∠CQB=30°,
∵点E、P、P1、C1四点共线,
∴C1E垂直平分BC,
∴∠ECP=∠EBP= =30°,
∴∠PCQ=90°,
同理∠PEQ=90°,
∴PQ=2PC=2PE,
∴PQ=PC+PE,
∴BQ=PB+PC+PE,
∵,
∴的最小值为.
3.
(1)证明:在BA上截取BG=BE,连结GE,
∵四边形ABCD为正方形,
∴AB=BC,∠B=90°,∠BCD=90°,
∵BG=BE,
∴AB-BG=BC-BE,即AG=EC,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∵AE⊥EF,
∴∠AEF=90°,
∴∠1+∠BEA=∠BEA+∠2=90°,
∴∠1=∠2,
∵CF平分∠DCB的外角,
∴∠DCF=45°,
∴∠ECF=∠ECD+∠DCF=90°+45°=135°,
∴∠AGE=∠ECF,
在△AGE和△ECF中,
∴△AGE≌△ECF(ASA),
∴AE=EF;
(2)AE=EF应然成立
证明:∵四边形ABCD为正方形,
∴AB=BC,∠ABE=90°,
延长BA到G,使BG=BE,
∴BG-AB=BE-BC,即GA=CE,∠AGE=45°,
∵AE⊥EF,
∴∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
∴180°-∠BAE=180°-∠HEF即∠GAE=∠CEF,
∵CF平分∠HCB的外角,
∴∠ECF=45°,
∴∠AGE=∠ECF,
在△AGE和△ECF中,
∴△AGE≌△ECF(ASA),
∴AE=EF;
(3)存在,理由如下,
证明:在AB上截取AM=BE,AE与MD交于N,
∵四边形ABCD为正方形,
∴∠DAM=∠ABE=90°,AD=AB,
在△ABE和△DAM中,
∴△ABE≌△DAM(SAS),
∴AE=DM,∠ADM=∠BAE,
∵∠AMD+∠ADM=∠BAE+∠AMD=90°,即∠AMN+∠MAN=90°,
∴∠ANM=180°-90°=90°,
∴AE⊥MD,
∵AE⊥EF,
∴MD∥EF,
∵△AGE≌△ECF,
∴AE=EF,
∴DM=EF,
∵MDEF,且MD=EF,
∴四边形DMEF是平行四边形.
4.
解:(1)四边形是平行四边形,
,
当从运动到时,
,
解得
当秒时,四边形是平行四边形;
(2)若点、分别沿、运动时,
,
即,
解得(秒
若点返回时,,
则
解得(秒.
故当或15秒时,以,,,为顶点的梯形面积等;
(3)当时
作于,则,
,
秒;
当时,,,
解得(秒,
综上可知,当秒或秒时,是等腰三角形.
5.
解:(1)过D作DH⊥BC于H,如图:
∵AD∥BC,∠B=90°,DH⊥BC,
∴四边形ABHD是矩形,
∴DH=AB=8,BH=AD=20,
在Rt△DHC中,CH===6,
∴BC=BH+CH=20+6=26(cm),
故答案为:26;
(2)如图:
根据题意可得:AP=2t,CQ=3t,
∵AD∥BC,
∴四边形PQCD是平行四边形,只需PD=CQ,即20﹣2t=3t,
解得t=4,
(3)如图:
∵AD∥BC,∠B=90°,
∴四边形PQBA是矩形,只需AP=BQ,即2t=26﹣3t,
解得t=5.2;
(4)存在,理由如下:
①若CD=DQ,过D作DH⊥BC于H,如图:
由(1)可知:CH=6,
∵CD=DQ,DH⊥BC,
∴CQ=2CH=12,
∴3t=12,
∴t=4,
②若CD=CQ,如图:
∴3t=10,
∴t=,
③若DQ=CQ,过D作DH⊥BC于H,如图:
在Rt△DQH中,QH=CQ﹣CH=3t﹣6,DH=8,DQ=CQ=3t,
由勾股定理得:(3t﹣6)2+82=(3t)2,
∴t=,
综上所述,△DQC是等腰三角形,t的值为:4或或.
6.
解:(1)如图1,过点D作于点E,则四边形ABED为矩形,
∴,,
∵,,,
∴,
由勾股定理得:,
∴;
(2)①如图2,
∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,且P在BC上,
∵DQ=AD-AQ=16-t,CP=21-2t,
∴16-t=21-2t,
解得:t=5,
∴当t=5秒时,四边形PQDC是平行四边形;
当点P在BC延长线上时,
∴16-t=2t-21,
解得:t=,
∴t=5秒或秒时,P、Q、D、C为顶点的四边形为平行四边形;
②当PQ=PD时,
如图3,作PH⊥AD于H,则HQ=HD,
∵QH=HD=QD=(16-t),
∵AH=BP,
∴2t=(16-t)+t,
∴t= ;
当PQ=QD时,QH=AH-AQ=BP-AQ=2t-t=t,QD=16-t,
∵QD2=PQ2=t2+122,
∴(16-t)2=122+t2,
解得:t=.
综上可知,当t=秒或秒时,△PQD是等腰三角形.
7.
解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,
∵DQ=AD﹣AQ=16﹣t,
CP=21﹣2t,
∴16﹣t=21﹣2t,
解得:t=5,
当P从C运动到B时,
∵DQ=AD﹣AQ=16﹣t,
CP=2t﹣21,
∴16﹣t=2t﹣21,
解得:t=,
∴当t=5或秒时,四边形PQDC是平行四边形;
(2)若点P、Q分别沿AD、BC运动时,
(DQ+CP) AB=60,
即(16﹣t+21﹣2t)×12=60,
解得:t=9(秒),
若点P返回时,CP=2t﹣2,
则(16﹣t+2t﹣21))×12=60,
解得:t=15(秒).
故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2;
(3)当PQ=PD时,作PH⊥AD于H,则HQ=HD,
∵QH=HD=QD=(16﹣t),
∵AH=BP,
∴2t=(16﹣t)+t,
∴t=秒;
当PQ=QD时,QH=AH﹣AQ=BP﹣AQ=2t﹣t=t,QD=16﹣t,
∵QD2=PQ2=t2+122,
∴(16﹣t)2=122+t2,
解得t=(秒);
当QD=PD时,DH=AD﹣AH=AD﹣BP=16﹣2t,
∵QD2=PD2=PH2+HD2=122+(16﹣2t)2,
∴(16﹣t)2=122+(16﹣2t)2,
即3t2﹣32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=秒或秒时,△PQD是等腰三角形.
8.
解:(1)是等边三角形,
,
,
,
,
,
由题意得:,,则,
,
解得:,
当为时,;
(2)过点作于,过点作于,如图1所示:
,
是等边三角形,
,
,
,,
,,
在中,由勾股定理得:,
在中,由勾股定理得:,
,
,
,
,
是等边三角形,
,
,
,
,
在中,由勾股定理得:,
,
,
当点在线段上时,与的关系式为:;
(3)存在,理由如下:
①当四边形是平行四边形时,如图2所示:
则,
,
,
,
是等边三角形,
,
,
,
,
;
②当四边形是平行四边形时,如图3所示:
则,
同①得:是等边三角形,
,
,
,
,
;
综上所述,当为或时,使得以,,,为顶点的四边形是平行四边形.
9.
(1),,
,
,
是等腰
是等腰
.
(2),
当时,四边形是平行四边形
是等腰
,
解得:.
当时,四边形是平行四边形
(3)如图:过作,连接,
又
是等腰
,
.
四边形是平行四边形
点为对角线的交点
即总是的中点.
(4)由(3)四边形是平行四边形
是等腰三角形
所以为顶角
,
.
,
解得:.
当,使得是等腰三角形.
10.
(1)证明:∵四边形ABCD是平行四边形,点O为AC的中点,
∴AE∥PC,AO=OC,
∴∠EAO=∠PCO,∠AOE=∠COP,
∴△AEO△CPO,
∴PO=OE;
(2)∵CA⊥AB,且PO⊥AC,
∴PO∥AB,即EP∥AB,
∵四边形ABCD是平行四边形,
∴AE∥BP,
∵CA⊥AB,且AB=6cm,AC=8cm,
∴BC=(cm),
∴四边形ABPE是平行四边形,
∵点O为AC的中点,且PO∥AB,
∴BP=PC=BC=5(cm);
(3)四边形ABPE的周长为:AB+BP+PE+AE,
由(1)知△AEO△CPO,则AE=CP,
∴BP+AE=BP+CP=BC=10,
∴四边形ABPE的周长为:6+10+PE=16+PE,
则PE最小时,四边形ABPE的周长最小,
∴当PE⊥BC时,PE最小(垂线段最短),
∵BCPE=ABAC,
∴PE=(cm),
∴四边形ABPE的周长最小值为16+=(cm),
∵△AEO△CPO,
∴PO=EO=PE=(cm),OC=AC=(cm),
∴PC=(cm),
∴BP=BC-PC=(cm),
故答案为:,.
.
11.
(1)x2﹣12x+32=0,
解得x1=4,x2=8,
∵OC>OA,
∴OA=4,OC=8,
故B点坐标为(8,4)
(2)由对折可知,∠DAC=∠BAC,
又∵四边形OABC为矩形,
∴AB//OC,∠BAC=∠ACO
∴∠DAC=∠ACO,
∴AD=CD,
设AD=x,则OD=8-x,
在中,满足有
化简得
解得x=5,
故OD=8-5=3
故D点坐标为(3,0)
由平行四边形性质可知P1(3,4),P2(13,4),P3(3,-4)时D、C、B、P四点形成的四边形为平行四边形.
12.
解:(1)∵在平行四边形中,,,
由运动知,AQ=16 t,BP=2t,
∵四边形ABPQ为平行四边形,
∴AQ=BP,
∴16 t=2t
∴t=,
即:t=s时,四边形ABPQ是平行四边形;
(2)过点A作AE⊥BC于E,如图,
在Rt△ABE中,∠B=30°,AB=8,
∴AE=4,
由运动知,BP=2t,DQ=t,
∵四边形ABCD是平行四边形,
∴AD=BC=16,
∴AQ=16 t,
∴y=S四边形ABPQ=(BP+AQ) AE=(2t+16 t)×4=2t+32(0<t≤8);
(3)由(2)知,AE=4,
∵BC=16,
∴S四边形ABCD=16×4=64,
由(2)知,y=S四边形ABPQ=2t+32(0<t≤8),
∵四边形ABPQ的面积是四边形ABCD的面积的四分之三
∴2t+32=×64,
∴t=8;
如图,
当t=8时,点P和点C重合,DQ=8,
∵CD=AB=8,
∴DP=DQ,
∴∠DQC=∠DPQ,
∴∠D=∠B=30°,
∴∠DQP=75°;
(4)①当AB=BP时,BP=8,
即2t=8,t=4;
②当AP=BP时,如图,
∵∠B=30°,
过P作PM垂直于AB,垂足为点M,
∴BM=4,,
解得:BP=,
∴2t=,
∴t=
③当AB=AP时,同(2)的方法得,BP=,
∴2t=,
∴t=
所以,当t=4或 或时,△ABP为等腰三角形.
13.
(1)证明:根据题意得:AD=4tcm,BE=2tcm,
∵,
∴CD=(60-4t)cm,
∵, ,
∴∠C=30°,
∴ ,
∵,
∴, ,
∴AE=(30-2t)cm,
∴AE=DF,,
∴四边形是平行四边形;
(2)解: 若点恰好在的垂直平分线上,则AD=DF,
∴4t=30-2t,
解得:t=5,
即当为5秒时,动点恰好在的垂直平分线上;
(3)解:存在,理由如下:
如图,当∠FDE=90°时,
∵∠DFC=∠B=∠FDE=90°,
∴四边形BEDF是矩形,
∴DF=BE=2t,DE∥BC,
∴∠ADE=∠C=30°,
∴AD=2AE=60-4t,
又∵AD=4t,
∴4t=60-4t,
解得:;
如图,当∠DEF=90°时,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴∠ADE=∠DEF=90°,
∵∠A=60°,
∴∠AED=30°,
∴AE=2AD,即30-2t=2×4t,
解得:t=3;
综上所述,当t=3或时,是直角三角形.
14.
解:(1)如图,作轴,垂足为点E.
∵直线与x轴,y轴分别交于点A,B,
∴当时,,当时,.
∴点A,B的坐标分别是,.
∴.
∵,
∴.
∵点C的坐标是,
∴,.
∴.
∴
∵,
∴.
∴,
即∠ABC的度数是90°.
(2)如图,四边形ABCD是平行四边形,作轴,垂足为点F.
∴,∠AFD=90°.
∵,
∴四边形ABCD是矩形.
∴.
∵,
∴.
∴.
∵,
∴.
∴,.
∴.
∴点D的坐标是.
15.
解:(1)平行四边形ABCD中,
AD=6
BC=6,
C(3,0),
B(﹣3,0)
故答案为:B(﹣3,0);
(2)∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵OA=4,
∴D(6,4),
∵S△AOE=×4×OE=,
∴OE=,
∴E(,0),
设经过D、E两点的直线解析式为:y=kx+b,
把点D(6,4),E(,0)代入得:,
解得:k=,b=﹣,
∴经过D、E两点的直线解析式为:y=x﹣;
(3)存在;N的坐标为(﹣5,4)或(5,4)或(0,-4)或(,4),理由如下:
分两种情况讨论,
①若以AC为边,CF为边,如图,
当点F在点C的右侧时,
四边形是菱形,
A(0,4),
(5,4)
当点F在点C的左侧时,
四边形是菱形,
A(0,4),
(-5,4);
若以AC为边,CF为对角线,如图,
四边形是菱形,
,且
A(0,4),
(0,-4);
②若以AC为对角线,如图,
此时菱形中,,
在中
(,4)
综上所述,存在点F使以A,C,F,N为顶点的四边形为菱形,N的坐标为(﹣5,4)或(5,4)或(0,-4)或(,4).
16.
解:(1)由旋转知AC=A,
∵∠CA=30°,
∴∠AC==75°;
(2)△DCE是等边三角形,
理由:在Rt△ABC中,∠ACB=90°,AB=AC,
∴∠ABC=∠BAC=45°,
由(1)知,∠AC=75°,
∴∠BCE=90°﹣∠AC=15°,
∴∠AEC=∠ABC+∠BCE=60°,
∵∠ADC+∠CDE=180°,∠ADC=120°,
∴∠CDE=60°,
∴∠CDE=∠DEC=∠ECD=60°,
∴△DCE是等边三角形;
(3)①当m=90°时,四边形ACB为平行四边形,如图3所示:
∵∠ACB=90°,∠BA=90°,
∴∠ACB+∠BA=180°,
∴,
∵A=AC,AC=BC,
∴A=BC,
∴四边形ACB为平行四边形;
②当m=270°时,四边形ACBC′为平行四边形,如图4所示:
当m=270°时,∠AC=90°,
∴∠AC=∠ACB,
∴A=BC,
∵A=CB,
∴四边形ACB为平行四边形,
综上所述,当m=90°或m=270°时,以A、B、C、四点组成的四边形为平行四边形.
17.
解:(1)过点作,交延长线于,过点作,交的延长线于,
四边形是平行四边形,
,,,,
,,
,
,,
,,
四边形的面积,
,
,
∴
四边形的面积
,
四边形的面积,
则当有最小值时,四边形的面积有最大值,
,
,
∵DN≤3,
∴4-DM≤3,
∴DM≥1,
当时,四边形的面积,
故答案为;
(2)存在,
设,
,
,
,
的周长,
当时,的周长的最小值为;
(3)与的周长之和不是定值,
理由如下:如图3,过点作,交的延长线于,过点作于,
,,
四边形是平行四边形,
,,
,
设,则,
,
,
,
,
,
,
,
,
与的周长之和不是定值,
当时,与的周长之和的最小值为15.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
