浙教版八年级数学下册试题 6.2 反比例函数的图象和性质同步练习(含答案)
文档属性
| 名称 | 浙教版八年级数学下册试题 6.2 反比例函数的图象和性质同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 990.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 10:21:21 | ||
图片预览




文档简介
6.2 反比例函数的图象和性质
一、单选题
1.互不重合的两点,皆落于反比例函数图象上,当直线AB与第二象限角平分线垂直时,的值等于( )
A. B.1 C. D.7
2.已知,,在反比例函数上,则,,的大小关系为
A. B. C. D.
3.已知反比例函数的图象上有两点A(a-3,2b),B(a,b-2),且a<0,则的取值范围是( )
A. B. C. D.
4.若,则x的取值范围( )
A.B.或 C.或 D.以上答案都不对
5.如果点A1(x1,y1)和点A1(x2,y2)是双曲线上的两个点,且当时x1<x2<0时,y1<y2,那么函数和函数y=kx﹣k的图象大致是( )
A. B. C. D.
6.如图平面直角坐标系中,菱形的边在轴上,反比例函数的图象经过菱形对角线的交点,且与边交于点,点的坐标为,则的面积为( )
A. B. C. D.
7.如图,在直角坐标系中,以坐标原点,,为顶点的,其两个锐角对应的外角角平分线相交于点,且点恰好在反比例函数的图象上,则的值为( )
A.36 B.25 C.16 D.9
8.已知反比例函数的图象经过平移后可以得到函数的图象,关于新函数,下列结论正确的是( )
A.当时,随的增大而增大 B.该函数的图象与轴有交点
C.该函数图象与轴的交点为 D.当时,的取值范围是
9.如图,在第一象限内,点A,B在反比例函数的图象上,点C在反比例函数()的图象上,轴,轴,若,,则k的值为( )
A.18 B.21 C.24 D.27
10.函数 和在第一象限内的图象如图,点P是的图象上一动点轴于点C,交的图象于点A,轴于点D,交的图象于点B.给出如下结论:
①与的面积相等;
②与始终相等;
③四边形的面积大小不会发生变化;
④.
其中所有正确结论有( )个.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.函数的图象不经过第________象限.
12.函数(a为常数)的图像上三点(—1, ),(, ),(, ),则函数值、、的大小关系是________________.
13.已知在平面直角坐标系中,有两定点、,是反比例函数图象上动点,当为直角三角形时,点坐标为________.
14.已知函数是反比例函数,且当x<0时,y随着x的增大而增大,则m的取值是_____.
15.如图,已知点A是一次函数图象上一点,过点A作轴的垂线,是上一点在A上方,在的右侧以为斜边作等腰直角三角形,反比例函数的图象过点,,若的面积为,则的面积是______.
如图,已知点是双曲线在第一象限上的一动点,连接,以为一边作等腰直角三角形(),点在第四象限,随着点的运动,点的位置也不断的变化,但始终在某个函数图像上运动,则这个函数表达式为______.
17.如图,已知,,,…,…是轴上的点,且,分别过点,,,…,,…作轴的垂线交反比例函数的图象于点,,,…,,过点作于点,过点作于点,…,记的面积为,的面积为,的面积为.则______.
18.如图,点A,B,C在反比例函数的图象上,且直线AB经过原点,点C在第二象限上,连接AC并延长交x轴于点D,连接BD,若△BOD的面积为9,则=_____.
三、解答题
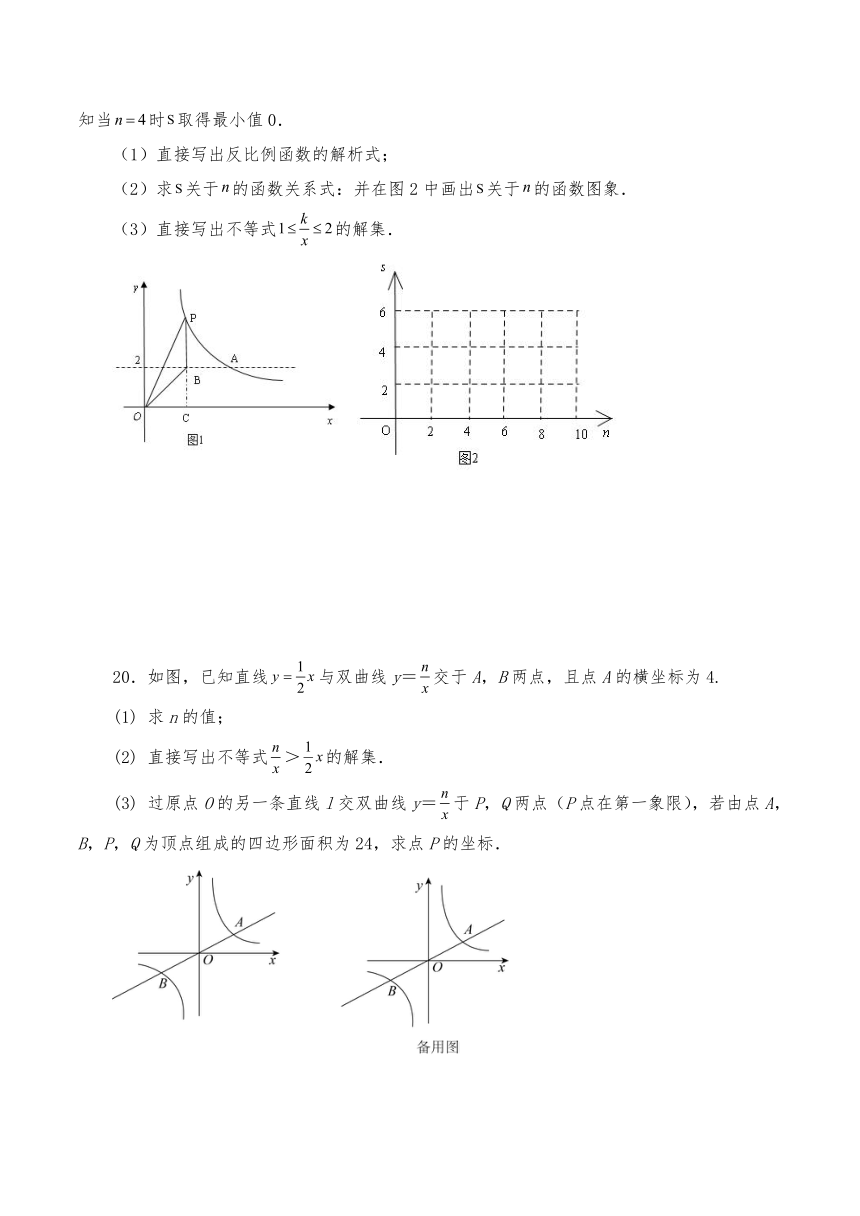
19.如图1,反比例函数()图象与直线相交于点,点是反比例函数图象上的动点,过点作轴于,交直线于.设点的横坐标为,的面积为.已知当时取得最小值0.
(1)直接写出反比例函数的解析式;
(2)求关于的函数关系式:并在图2中画出关于的函数图象.
(3)直接写出不等式的解集.
20.如图,已知直线与双曲线y=交于A,B两点,且点A的横坐标为4.
求n的值;
直接写出不等式>的解集.
过原点O的另一条直线l交双曲线y=于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
21.已知反比例函数图象经过一、三象限.
(1)判断点在第几象限
(2)若点,是反比例函数图象上的两点,试比较a,b,c的大小关系
(3)设反比例函数,已知,且满足当时,函数的最大值是;当时,函数的最小值是.求x为何值时,.
22.如图,已知一次函数与反比例函数的图象交于第一象限内的点和,与x轴交于点C.
分别求出这两个函数的表达式;
①观察图象,直接写出不等式的解集;②请连接OA、OB,并计算△AOB的面积;
是否存在坐标平面内的点P,使得由点O,A,C,P组成的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.[探究函数的图象与性质]
(1) 函数的自变量x的取值范围是 ;
(2) 下列四个函数图象中函数的图象大致是 ;
(3) 对于函数,求当时,y的取值范围.
请将下列的求解过程补充完整.
解:∵
∴ .
∵,∴ .
[拓展运用]
若函数,则y的取值范围 .
24.(1)探究新知:
如图,已知三角形ABC与三角形ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
如图,点M、N在反比例函数的图像是哪个,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E、F,试证明:.
答案
一、单选题
1.C 2.A 3.C 4.C 5.C 6.A 7.A 8.C 9.D 10.C
二、填空题
11.四
12.<<
13.或
14.-3
15.
16..
17.
18.
三、解答题
19.
解:(1)∵当时取得最小值0,
∴此时点P与点B重合,
又∵点B在直线上,
∴点P的坐标为(4,2),
把点P(4,2)代入中,
解得:k=8,
∴反比例函数的解析式为;
(2)如下图:依题意知点
,
①当时,
②当时,
关于的函数图象如下:
说明:图象中点应为空心,不为空心的扣1分;另一支射线无论长短不扣分.
(3)由(1)知反比例函数的解析式为,
当y=1时,x=8,
当y=2时,x=4,
∴不等式的解集为.
20.(1)解:把点A的横坐标4.代入直线得,y=2,
∴点A(4,2),
把点A(4,2)代入到中得n=8;
(2)解:由对称性可知点B(﹣4,﹣2)
∴不等式>的解集为:0<x<4或x<﹣4;
(3)解:如图:过点P作PN⊥x轴于N,过点A作AM⊥x轴与M,设点P(x,),则PN=,ON=x,
由对称性得,OA=OB,OP=OQ,
∴四边形APBQ是平行四边形,
∴S△AOP=S APBQ=×24=6=S梯形AMNP,
①当点P在点A上方的曲线上,
(+2)(4﹣x)=6,
整理得,x2+6x﹣16=0,
解得:x1=2,x2=﹣8(舍去),
当x=2时,y==4,
∴点P(2,4),
②当点P在点A下方的曲线上,
(+2)(x﹣4)=6,
整理得,x2-6x-16=0,
解得:x1=8,x2=-2(舍去),
当x=8时,y==1,
∴点P(8,1),
因此符合条件的点P有两个,P1(2,4),P2(8,1)
∴点P的坐标为:(2,4)或(8,1).
21.
解:(1)反比例函数图象经过一、三象限,
,,
点在第二象限;
(2)反比例函数图象经过一、三象限,
在每一象限内随的增大而减小,
又点,在反比例函数上,
可得,
解得:a>c>b,
,,的大小关系为:a>c>b;
(3),
反比例函数位于第二、四象限,
在每一象限内随的增大而增大,
又,当时,函数的最大值是;当时,函数的最小值是,
当时,;当时,,
,
解得:(不合题意,舍去)或,
将时,代入中,
,
,,
若,
,
解得:,
经检验是原方程的解,
当时,.
22.
(1)解:∵点A(1,6)在反比例函数y=的图象上,
∴6=,
解得:k2=6,
∴反比例函数的表达式是:y=;
∵B(6,m)在反比例函数y=的图象上,
∴m==1,
∴B(6,1),
将点A(1,6),B(6,1)代入y=k1x+b,可得:
,
解得:,
∴一次函数表达式是:y=﹣x+7;
(2)解:①∵点A(1,6),B(6,1),
∴不等式k1x+b≥的解集是:x<0或1≤x≤6;
故答案为:x<0或1≤x≤6;
②如图所示,过点A作AD⊥x轴于D,过点B作BE⊥x轴于B,
∴,
∵A(1,6),B(6,1),
∴OD=1,AD=6,OE=6,BE=1,
∴DE=5,
∵,
∴;
(3)解:∵C是直线AB与x轴的交点,
∴点C的坐标为(7,0),
如图3-1所示:当AP为边时,
∴AP∥OC, AP=OC=7,
∵A(1,6),
∴P点坐标为:(8,6)或(-6,6);
当AP为对角线时,如图3-2所示,
∵AP与OC的中点坐标相同,
∴ ,
∴ ,
∴点P的坐标为(6,-6);
综上所述存在点P的坐标为(8,6)或(﹣6,6)或(6,﹣6)使得由点O,A,C,P组成的四边形是平行四边形.
23.
解:(1)函数的自变量x的取值范围是;
故答案为:;
(2)∵中以及反比例函数的性质,,图象过一、三象限可得:函数的图象大致是C;
故答案为:C;
解:∵
∴.
∵,
∴.
故答案为:4,4
(4)①当时,
∵,
∴.
②当时,
∵,
∴.
故答案为:或.
24.
解:(1)分别过点C,D,作CG⊥AB,DH⊥AB,垂足为G,H,
则∠CGA=∠DHB=90°,CG∥DH.
∵△ABC与△ABD的面积相等,
∴ CG=DH;
∴ 四边形CGHD为平行四边形.
∴ AB∥CD.
(2)证明:连接MF,NE 设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
∵点M,N在反比例函数 (k>0)的图像上,
∴ .
∵ME⊥y轴,NF⊥x轴,
∴ OE=y1,OF=x2.
∴ S △EFM=
S △EFN= .
∴S △EFM =S △EFN.
所以由(1)中的结论可知:MN∥EF.
一、单选题
1.互不重合的两点,皆落于反比例函数图象上,当直线AB与第二象限角平分线垂直时,的值等于( )
A. B.1 C. D.7
2.已知,,在反比例函数上,则,,的大小关系为
A. B. C. D.
3.已知反比例函数的图象上有两点A(a-3,2b),B(a,b-2),且a<0,则的取值范围是( )
A. B. C. D.
4.若,则x的取值范围( )
A.B.或 C.或 D.以上答案都不对
5.如果点A1(x1,y1)和点A1(x2,y2)是双曲线上的两个点,且当时x1<x2<0时,y1<y2,那么函数和函数y=kx﹣k的图象大致是( )
A. B. C. D.
6.如图平面直角坐标系中,菱形的边在轴上,反比例函数的图象经过菱形对角线的交点,且与边交于点,点的坐标为,则的面积为( )
A. B. C. D.
7.如图,在直角坐标系中,以坐标原点,,为顶点的,其两个锐角对应的外角角平分线相交于点,且点恰好在反比例函数的图象上,则的值为( )
A.36 B.25 C.16 D.9
8.已知反比例函数的图象经过平移后可以得到函数的图象,关于新函数,下列结论正确的是( )
A.当时,随的增大而增大 B.该函数的图象与轴有交点
C.该函数图象与轴的交点为 D.当时,的取值范围是
9.如图,在第一象限内,点A,B在反比例函数的图象上,点C在反比例函数()的图象上,轴,轴,若,,则k的值为( )
A.18 B.21 C.24 D.27
10.函数 和在第一象限内的图象如图,点P是的图象上一动点轴于点C,交的图象于点A,轴于点D,交的图象于点B.给出如下结论:
①与的面积相等;
②与始终相等;
③四边形的面积大小不会发生变化;
④.
其中所有正确结论有( )个.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.函数的图象不经过第________象限.
12.函数(a为常数)的图像上三点(—1, ),(, ),(, ),则函数值、、的大小关系是________________.
13.已知在平面直角坐标系中,有两定点、,是反比例函数图象上动点,当为直角三角形时,点坐标为________.
14.已知函数是反比例函数,且当x<0时,y随着x的增大而增大,则m的取值是_____.
15.如图,已知点A是一次函数图象上一点,过点A作轴的垂线,是上一点在A上方,在的右侧以为斜边作等腰直角三角形,反比例函数的图象过点,,若的面积为,则的面积是______.
如图,已知点是双曲线在第一象限上的一动点,连接,以为一边作等腰直角三角形(),点在第四象限,随着点的运动,点的位置也不断的变化,但始终在某个函数图像上运动,则这个函数表达式为______.
17.如图,已知,,,…,…是轴上的点,且,分别过点,,,…,,…作轴的垂线交反比例函数的图象于点,,,…,,过点作于点,过点作于点,…,记的面积为,的面积为,的面积为.则______.
18.如图,点A,B,C在反比例函数的图象上,且直线AB经过原点,点C在第二象限上,连接AC并延长交x轴于点D,连接BD,若△BOD的面积为9,则=_____.
三、解答题
19.如图1,反比例函数()图象与直线相交于点,点是反比例函数图象上的动点,过点作轴于,交直线于.设点的横坐标为,的面积为.已知当时取得最小值0.
(1)直接写出反比例函数的解析式;
(2)求关于的函数关系式:并在图2中画出关于的函数图象.
(3)直接写出不等式的解集.
20.如图,已知直线与双曲线y=交于A,B两点,且点A的横坐标为4.
求n的值;
直接写出不等式>的解集.
过原点O的另一条直线l交双曲线y=于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
21.已知反比例函数图象经过一、三象限.
(1)判断点在第几象限
(2)若点,是反比例函数图象上的两点,试比较a,b,c的大小关系
(3)设反比例函数,已知,且满足当时,函数的最大值是;当时,函数的最小值是.求x为何值时,.
22.如图,已知一次函数与反比例函数的图象交于第一象限内的点和,与x轴交于点C.
分别求出这两个函数的表达式;
①观察图象,直接写出不等式的解集;②请连接OA、OB,并计算△AOB的面积;
是否存在坐标平面内的点P,使得由点O,A,C,P组成的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.[探究函数的图象与性质]
(1) 函数的自变量x的取值范围是 ;
(2) 下列四个函数图象中函数的图象大致是 ;
(3) 对于函数,求当时,y的取值范围.
请将下列的求解过程补充完整.
解:∵
∴ .
∵,∴ .
[拓展运用]
若函数,则y的取值范围 .
24.(1)探究新知:
如图,已知三角形ABC与三角形ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
如图,点M、N在反比例函数的图像是哪个,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E、F,试证明:.
答案
一、单选题
1.C 2.A 3.C 4.C 5.C 6.A 7.A 8.C 9.D 10.C
二、填空题
11.四
12.<<
13.或
14.-3
15.
16..
17.
18.
三、解答题
19.
解:(1)∵当时取得最小值0,
∴此时点P与点B重合,
又∵点B在直线上,
∴点P的坐标为(4,2),
把点P(4,2)代入中,
解得:k=8,
∴反比例函数的解析式为;
(2)如下图:依题意知点
,
①当时,
②当时,
关于的函数图象如下:
说明:图象中点应为空心,不为空心的扣1分;另一支射线无论长短不扣分.
(3)由(1)知反比例函数的解析式为,
当y=1时,x=8,
当y=2时,x=4,
∴不等式的解集为.
20.(1)解:把点A的横坐标4.代入直线得,y=2,
∴点A(4,2),
把点A(4,2)代入到中得n=8;
(2)解:由对称性可知点B(﹣4,﹣2)
∴不等式>的解集为:0<x<4或x<﹣4;
(3)解:如图:过点P作PN⊥x轴于N,过点A作AM⊥x轴与M,设点P(x,),则PN=,ON=x,
由对称性得,OA=OB,OP=OQ,
∴四边形APBQ是平行四边形,
∴S△AOP=S APBQ=×24=6=S梯形AMNP,
①当点P在点A上方的曲线上,
(+2)(4﹣x)=6,
整理得,x2+6x﹣16=0,
解得:x1=2,x2=﹣8(舍去),
当x=2时,y==4,
∴点P(2,4),
②当点P在点A下方的曲线上,
(+2)(x﹣4)=6,
整理得,x2-6x-16=0,
解得:x1=8,x2=-2(舍去),
当x=8时,y==1,
∴点P(8,1),
因此符合条件的点P有两个,P1(2,4),P2(8,1)
∴点P的坐标为:(2,4)或(8,1).
21.
解:(1)反比例函数图象经过一、三象限,
,,
点在第二象限;
(2)反比例函数图象经过一、三象限,
在每一象限内随的增大而减小,
又点,在反比例函数上,
可得,
解得:a>c>b,
,,的大小关系为:a>c>b;
(3),
反比例函数位于第二、四象限,
在每一象限内随的增大而增大,
又,当时,函数的最大值是;当时,函数的最小值是,
当时,;当时,,
,
解得:(不合题意,舍去)或,
将时,代入中,
,
,,
若,
,
解得:,
经检验是原方程的解,
当时,.
22.
(1)解:∵点A(1,6)在反比例函数y=的图象上,
∴6=,
解得:k2=6,
∴反比例函数的表达式是:y=;
∵B(6,m)在反比例函数y=的图象上,
∴m==1,
∴B(6,1),
将点A(1,6),B(6,1)代入y=k1x+b,可得:
,
解得:,
∴一次函数表达式是:y=﹣x+7;
(2)解:①∵点A(1,6),B(6,1),
∴不等式k1x+b≥的解集是:x<0或1≤x≤6;
故答案为:x<0或1≤x≤6;
②如图所示,过点A作AD⊥x轴于D,过点B作BE⊥x轴于B,
∴,
∵A(1,6),B(6,1),
∴OD=1,AD=6,OE=6,BE=1,
∴DE=5,
∵,
∴;
(3)解:∵C是直线AB与x轴的交点,
∴点C的坐标为(7,0),
如图3-1所示:当AP为边时,
∴AP∥OC, AP=OC=7,
∵A(1,6),
∴P点坐标为:(8,6)或(-6,6);
当AP为对角线时,如图3-2所示,
∵AP与OC的中点坐标相同,
∴ ,
∴ ,
∴点P的坐标为(6,-6);
综上所述存在点P的坐标为(8,6)或(﹣6,6)或(6,﹣6)使得由点O,A,C,P组成的四边形是平行四边形.
23.
解:(1)函数的自变量x的取值范围是;
故答案为:;
(2)∵中以及反比例函数的性质,,图象过一、三象限可得:函数的图象大致是C;
故答案为:C;
解:∵
∴.
∵,
∴.
故答案为:4,4
(4)①当时,
∵,
∴.
②当时,
∵,
∴.
故答案为:或.
24.
解:(1)分别过点C,D,作CG⊥AB,DH⊥AB,垂足为G,H,
则∠CGA=∠DHB=90°,CG∥DH.
∵△ABC与△ABD的面积相等,
∴ CG=DH;
∴ 四边形CGHD为平行四边形.
∴ AB∥CD.
(2)证明:连接MF,NE 设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
∵点M,N在反比例函数 (k>0)的图像上,
∴ .
∵ME⊥y轴,NF⊥x轴,
∴ OE=y1,OF=x2.
∴ S △EFM=
S △EFN= .
∴S △EFM =S △EFN.
所以由(1)中的结论可知:MN∥EF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
