八年级数学下册试题 6.3 反比例函数的应用--反比例函数对称性问题习题 -浙教版(含答案)
文档属性
| 名称 | 八年级数学下册试题 6.3 反比例函数的应用--反比例函数对称性问题习题 -浙教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 10:20:46 | ||
图片预览




文档简介
6.3 反比例函数的应用--反比例函数对称性问题
一、单选题
1.如图,若双曲线与它的一条对称轴交于A、B两点,则线段AB称为双曲线的“对径”.若双曲线的对径长是,则 k的值为( )
A.2 B.4 C.6 D.
2.如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=; ②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
A.①②③ B.②④ C.①③④ D.①④
3.如图,点A与点B关于原点对称,点C在第四象限,∠ACB=90°.点D是轴正半轴上一点,AC平分∠BAD,E是AD的中点,反比例函数()的图象经过点A,E.若△ACE的面积为6,则的值为( )
A. B. C. D.
4.已知某函数的图象C与函数的图象关于直线对称.下列命题:①图象C与函数的图象交于点;②点在图象C上;③图象C上的点的纵坐标都小于4,④,是图象C上任意两点,若,则.其中真命题是( )
A.①② B.①③④ C.②③④ D.①②④
5.如图,反比例函数y=(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
A.1+ B.4+ C.4 D.-1+
6.点关于y轴的对称点在反比例函数的图像上,下列说法不正确的是( )
A.y随x的增大而减小
B.点在该函数的图像上
C.当时,
D.该函数图像与直线的交点是(,)和(-,-)
7.如图,矩形的顶点坐标分别为,动点F在边上(不与重合),过点F的反比例函数的图象与边交于点E,直线分别与y轴和x轴相交于点D和G.给出下列命题:①若,则的面积为;②若,则点C关于直线的对称点在x轴上;③满足题设的k的取值范围是;④若,则.其中正确的命题个数是( )
A.1个 B.2个 C.3个 D.4个
8.已知某函数的图象C与函数的图象关于直线对称下列命题:①图象C与函数的图象交于点;②在图象C上;③图象C上的点的纵坐标都小于4;④,是图象C上任意两点,若,则,其中真命题是( )
A.①② B.①③④ C.②③④ D.①②③④
9.如图,一次函数和与反比例函数的交点分别为点、和,下列结论中,正确的个数是( )
①点与点关于原点对称;②;③点的坐标是;④是直角三角形.
A.1 B.2 C.3 D.4
10.如图,矩形的边,,动点在边上(不与、重合),过点的反比例函数的图象与边交于点,直线分别与轴和轴相交于点和.给出以下命题:①若,则的面积为;②若,则点关于直线的对称点在轴上;③满足题设的的取值范围是;④若,则;其中正确的命题个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知A、B两点为反比例函数的图像上的动点,他们关于y轴的对称点恰好落在直线上,若点A、B的坐标分别为且,则________.
12.如图反比例函数的图像经过点,点与点关于轴对称,点是轴上一点,若的面积为2,则该反比例函数的解析式为_____________
13.如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O B .
(1)当点O 与点A重合时,点P的坐标是 ;
(2)设P(t,0),当O B 与双曲线有交点时,t的取值范围是 .
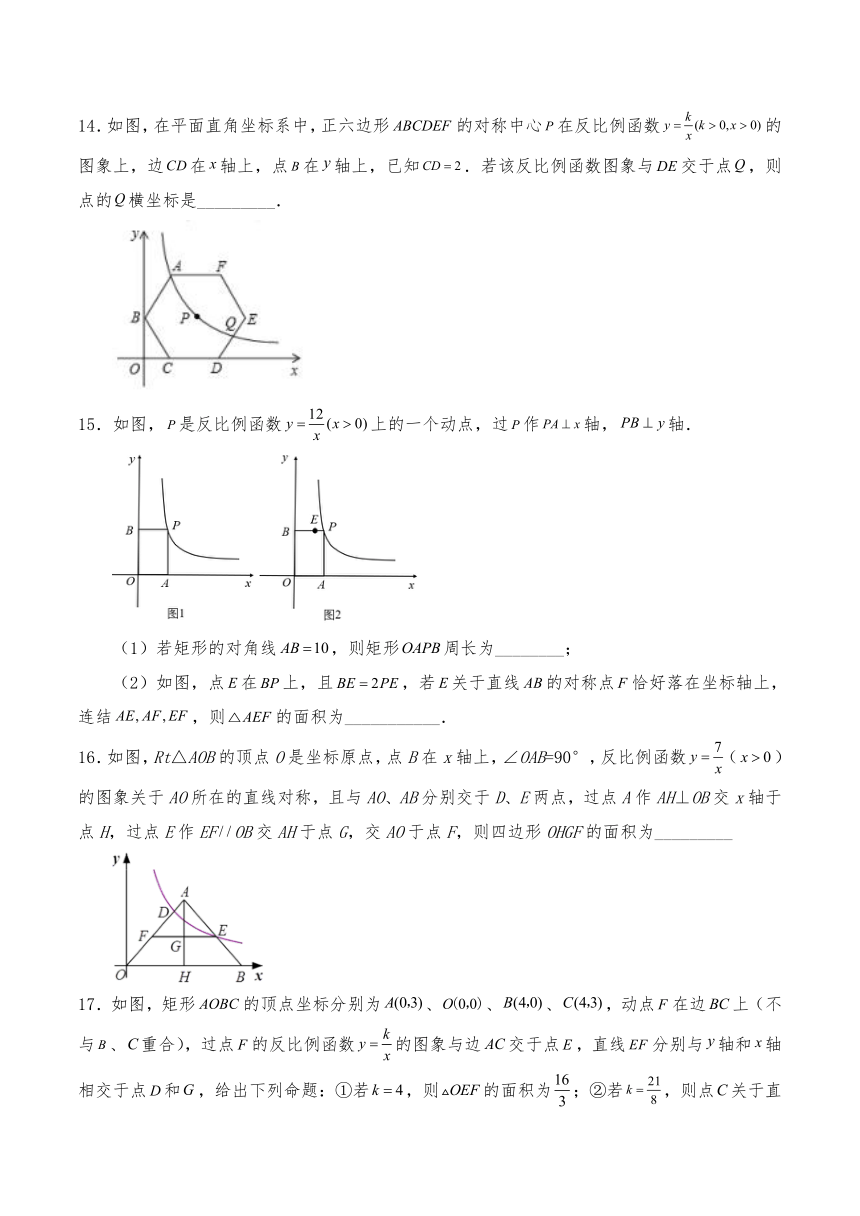
14.如图,在平面直角坐标系中,正六边形的对称中心在反比例函数的图象上,边在轴上,点在轴上,已知.若该反比例函数图象与交于点,则点的横坐标是_________.
15.如图,是反比例函数上的一个动点,过作轴,轴.
(1)若矩形的对角线,则矩形周长为________;
(2)如图,点在上,且,若关于直线的对称点恰好落在坐标轴上,连结,则的面积为___________.
16.如图,Rt△AOB的顶点O是坐标原点,点B在x轴上,∠OAB=90°,反比例函数()的图象关于AO所在的直线对称,且与AO、AB分别交于D、E两点,过点A作AH⊥OB交x轴于点H,过点E作EFOB交AH于点G,交AO于点F,则四边形OHGF的面积为_________
17.如图,矩形的顶点坐标分别为、、、,动点在边上(不与、重合),过点的反比例函数的图象与边交于点,直线分别与轴和轴相交于点和,给出下列命题:①若,则的面积为;②若,则点关于直线的对称点在轴上;③满足题设的的取值范围是;④若,则.其中正确的命题的序号是________.(写出所有正确命题的序号)
18.如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y=(k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是_____________.
三、解答题
19.综合与探究
如图1,反比例函数的图象经过点,点的横坐标是-2,点关于坐标原点的对称点为点,作直线.
判断点是否在反比例函数的图象上,并说明理由;
如图1,过坐标原点作直线交反比例函数的图象于点和点,点的横坐标是4,顺次连接,,和.求证:四边形是矩形;
已知点在轴的正半轴上运动,点在平面内运动,当以点,,和为顶点的四边形为菱形时,请直接写出此时点的坐标.
20.如图,一次函数的图像与反比例函数的图像交于点,与轴交于点,与轴交于点,轴于点,,点关于直线的对称点为点.
(1) 点是否在这个反比例函数的图像上?请说明理由;
(2) 连接、,若四边形为正方形.
①求、的值;
②若点在轴上,当最大时,求点的坐标.
21.如图,在平面直角坐标系中,直线与双曲线与相交于A,B两点(点A在点B的左侧).
(1)当时,求k的值;
(2)点B关于y轴的对称点为C,连接;
①判断的形状,并说明理由;
②当的面积等于16时,双曲线上是否存在一点P,连接,使的面积等于面积?若存在,求出点P的坐标,若不存在,请说明理由.
22.如图,矩形的面积为8,它的边位于x轴上.双曲线经过点A,与矩形的边交于点E,点B在双曲线上,连接并延长交x轴于点F,点G与点О关于点C对称,连接,.
(1)求k的值;
(2)求的面积;
(3)求证:四边形AFGB为平行四边形.
23.如图,直线与反比例函数的图象相交于点,与轴交于点.
(1) 求和的值.
(2) 若点与点关于直线对称,连接.
①求点的坐标;
②若点在反比例函数的图象上,点在轴上,以点为顶点的四边形能否为平行四边形?若能,直接写出点的坐标;若不能,请说明理由.
24.如图,菱形OABC的点B在y轴上,点C坐标为(12,5),双曲线的图象经过点A.
(1) 菱形OABC的边长为____;
(2) 求双曲线的函数关系式;
(3) ①点B关于点O的对称点为D点,过D作直线l垂直于y轴,点P是直线l上一个动点,点E在双曲线上,当P、E、A、B四点构成平行四边形时,求点E的坐标;
②将点P绕点A逆时针旋转90°得点Q,当点Q落在双曲线上时,求点Q的坐标.
答案
一、单选题
1.B 2.D 3.C 4.A 5.A 6.A 7.D 8.A 9.D 10.B
二、填空题
11.1
12.
13.(1)(4,0);(2)4≤t≤或≤t≤-4
14.
15. 4或
16.
17.①②
18.
19.
解:(1)结论:点在反比例函数的图象上,
理由如下:∵反比例函数的图象经过点,点的横坐标是-2,
∴把代入中,得,
∴点的坐标是,
∵点关于坐标原点的对称点为点,
∴点的坐标是,
把代入中,得,
∴点在反比例函数的图象上;
(2)证明:在反比例函数中令x=4则y=-2,
∵过坐标原点作直线交反比例函数的图象于点和点,
∴C,D关于原点对称,
∴C(4,-2),D(-4,2),OC=OD,
∵A,B关于原点对称,
∴OA=OB,
∴四边形ACBD是平行四边形,
∵CD=,AB=,
∴AB=CD,
∴四边形ACBD是矩形;
(3)设点P的坐标为,如图,
当四边形OBP1Q1是菱形时,可得,
∴,解得,
∴P1;
当四边形OBQ2P2是菱形时,可得,
∴,
∴P2;
当四边形OP3BQ3是菱形时,可得,
∴,
解得,
∴P3,
综上所述,满足条件的点的坐标分别为,和.
20.
(1)解:点在这个反比例函数的图像上.
理由如下:
一次函数的图像与反比例函数的图像交于点,
设点的坐标为,
点关于直线的对称点为点,
,平分,
连接交于,如图所示:
,
轴于,
轴,,
,
,
,
在Rt中,,
,
为边上的中线,即,
,
,
,
点在这个反比例函数的图像上;
(2)解:①四边形为正方形,
,垂直平分,
,
设点的坐标为,
,,
,
(负值舍去),
,,
把,代入得,
;
②延长交轴于,如图所示:
,,
点与点关于轴对称,
,则点即为符合条件的点,
由①知,,,
,,
设直线的解析式为,
,解得,
直线的解析式为,
当时,,即,故当最大时,点的坐标为.
21.
(1)解:设点B的坐标为,则点,则:
,
解得(负值已舍去),
故点B的坐标为,
将点B的坐标代入反比例函数表达式得∶,
解得∶;
(2)解:①为直角三角形,理由∶
设点,则点,
∵点A、C的横坐标相同,
∴轴,
∴点B关于y轴的对称点为C,
∴轴,
∴,
∴为直角三角形;
②由①得∶,
则的面积,
解得(负值已舍去),
∴点B的坐标为,C的坐标为,
将点B的坐标代入反比例函数表达式得∶,解得,
∴反比例函数表达式为①;
过点C作直线,交反比例函数于点P,则点P符合题设要求,
同样在AB下方等间隔作直线交反比例函数于点P,则点P也符合要求.
∵,
∴设直线m的表达式为,
将点C的坐标代入,解得,
故直线m的表达式为②,
根据图形的对称性,则直线n的表达式为③,
联立①②并解得∶
或,
联立①③并解得∶
或,
∴点P的坐标为或或或.
22.
(1)解:设,,
根据题意可知:,整理可得:.
(2)解:∵,
∴,
∵点E在,且点B和点E的横坐标相等,
∴,即,
设直线的函数解析式为:,将和代入可得:
,解得:,
故直线的函数解析式为:,
令,可得:,
∴,
∵,即,
∴,
∵点C的横坐标和点B的横坐标相等,
∴,
∴.
证明:∵,点G与点О关于点C对称,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形.
23.
解:(1)将点代入得:,
,
直线的表达式为,
把点代入,得:,
,
将代入得:,
;
①连接,过作轴于,如图:
,
,
是等腰直角三角形,
,
由点与点关于直线对称,知≌,
,即,
,
点的坐标为;
以点为顶点的四边形能为平行四边形,理由如下:
设,又,
Ⅰ若是对角线,则的中点重合,
,
解得,
;
Ⅱ若为对角线,则的中点重合;
,
解得,
;
Ⅲ若为对角线,则的中点重合,
,
解得,
,
综上所述,的坐标为或或.
24.
(1)解:如图所示,连接AC交y轴于J,
∵四边形OABC是菱形,
∴AC⊥OB,AJ=JC,OJ=BJ,
∵点C的坐标为(12,5),
∴AJ=JC=12,OJ=BJ=5,
∴,
故答案为:5;
(2)解:∵AJ=JC=12,OJ=BJ=5,
∴点A的坐标为(-12,5),
∵反比例函数经过点A(-12,5),
∴,
∴,
∴反比例函数解析式为;
(3)解:①设E点坐标为(m,),
∵OJ=BJ=5,
∴OB=10,
∴B点坐标为(0,10),
∵点B关于点O的对称点为D点,
∴D点坐标为(0,-10),
∴直线l为,
设P点坐标为(a,-10)
当AB是以P、E、A、B四点构成平行四边形的对角线时,
∵线段AB与线段PE的中点坐标相同,
∴,
∴,
∴点E的坐标为(,25);
如图所示,当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,
∵与的中点坐标相同,
∴,
∴,
∴的坐标为(12,-5);
同理可以求出当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,点的坐标为(,-15);
综上所述,当E点坐标为(,-5)或(4,-15)或(,25)时,以P、E、A、B四点构成的四边形是平行四边形;
②如图所示,过点A作AT⊥PD于T,过点Q作QR⊥AT于R,
∵点A的坐标为(-12,5),直线l为,
∴AT=15,
∵∠ATP=∠QRA=∠PAQ=90°,
∴∠PAT+∠APT=90°,∠PAT+∠QAR=90°,
∴∠APT=∠QAR,
又∵AP=QA,
∴△APT≌△QRA(AAS),
∴AT=RQ=15,
∴Q点的横坐标为3,
∵Q在反比例函数上,
∴,
∴点Q的坐标为(3,).
一、单选题
1.如图,若双曲线与它的一条对称轴交于A、B两点,则线段AB称为双曲线的“对径”.若双曲线的对径长是,则 k的值为( )
A.2 B.4 C.6 D.
2.如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=; ②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
A.①②③ B.②④ C.①③④ D.①④
3.如图,点A与点B关于原点对称,点C在第四象限,∠ACB=90°.点D是轴正半轴上一点,AC平分∠BAD,E是AD的中点,反比例函数()的图象经过点A,E.若△ACE的面积为6,则的值为( )
A. B. C. D.
4.已知某函数的图象C与函数的图象关于直线对称.下列命题:①图象C与函数的图象交于点;②点在图象C上;③图象C上的点的纵坐标都小于4,④,是图象C上任意两点,若,则.其中真命题是( )
A.①② B.①③④ C.②③④ D.①②④
5.如图,反比例函数y=(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
A.1+ B.4+ C.4 D.-1+
6.点关于y轴的对称点在反比例函数的图像上,下列说法不正确的是( )
A.y随x的增大而减小
B.点在该函数的图像上
C.当时,
D.该函数图像与直线的交点是(,)和(-,-)
7.如图,矩形的顶点坐标分别为,动点F在边上(不与重合),过点F的反比例函数的图象与边交于点E,直线分别与y轴和x轴相交于点D和G.给出下列命题:①若,则的面积为;②若,则点C关于直线的对称点在x轴上;③满足题设的k的取值范围是;④若,则.其中正确的命题个数是( )
A.1个 B.2个 C.3个 D.4个
8.已知某函数的图象C与函数的图象关于直线对称下列命题:①图象C与函数的图象交于点;②在图象C上;③图象C上的点的纵坐标都小于4;④,是图象C上任意两点,若,则,其中真命题是( )
A.①② B.①③④ C.②③④ D.①②③④
9.如图,一次函数和与反比例函数的交点分别为点、和,下列结论中,正确的个数是( )
①点与点关于原点对称;②;③点的坐标是;④是直角三角形.
A.1 B.2 C.3 D.4
10.如图,矩形的边,,动点在边上(不与、重合),过点的反比例函数的图象与边交于点,直线分别与轴和轴相交于点和.给出以下命题:①若,则的面积为;②若,则点关于直线的对称点在轴上;③满足题设的的取值范围是;④若,则;其中正确的命题个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知A、B两点为反比例函数的图像上的动点,他们关于y轴的对称点恰好落在直线上,若点A、B的坐标分别为且,则________.
12.如图反比例函数的图像经过点,点与点关于轴对称,点是轴上一点,若的面积为2,则该反比例函数的解析式为_____________
13.如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O B .
(1)当点O 与点A重合时,点P的坐标是 ;
(2)设P(t,0),当O B 与双曲线有交点时,t的取值范围是 .
14.如图,在平面直角坐标系中,正六边形的对称中心在反比例函数的图象上,边在轴上,点在轴上,已知.若该反比例函数图象与交于点,则点的横坐标是_________.
15.如图,是反比例函数上的一个动点,过作轴,轴.
(1)若矩形的对角线,则矩形周长为________;
(2)如图,点在上,且,若关于直线的对称点恰好落在坐标轴上,连结,则的面积为___________.
16.如图,Rt△AOB的顶点O是坐标原点,点B在x轴上,∠OAB=90°,反比例函数()的图象关于AO所在的直线对称,且与AO、AB分别交于D、E两点,过点A作AH⊥OB交x轴于点H,过点E作EFOB交AH于点G,交AO于点F,则四边形OHGF的面积为_________
17.如图,矩形的顶点坐标分别为、、、,动点在边上(不与、重合),过点的反比例函数的图象与边交于点,直线分别与轴和轴相交于点和,给出下列命题:①若,则的面积为;②若,则点关于直线的对称点在轴上;③满足题设的的取值范围是;④若,则.其中正确的命题的序号是________.(写出所有正确命题的序号)
18.如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y=(k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是_____________.
三、解答题
19.综合与探究
如图1,反比例函数的图象经过点,点的横坐标是-2,点关于坐标原点的对称点为点,作直线.
判断点是否在反比例函数的图象上,并说明理由;
如图1,过坐标原点作直线交反比例函数的图象于点和点,点的横坐标是4,顺次连接,,和.求证:四边形是矩形;
已知点在轴的正半轴上运动,点在平面内运动,当以点,,和为顶点的四边形为菱形时,请直接写出此时点的坐标.
20.如图,一次函数的图像与反比例函数的图像交于点,与轴交于点,与轴交于点,轴于点,,点关于直线的对称点为点.
(1) 点是否在这个反比例函数的图像上?请说明理由;
(2) 连接、,若四边形为正方形.
①求、的值;
②若点在轴上,当最大时,求点的坐标.
21.如图,在平面直角坐标系中,直线与双曲线与相交于A,B两点(点A在点B的左侧).
(1)当时,求k的值;
(2)点B关于y轴的对称点为C,连接;
①判断的形状,并说明理由;
②当的面积等于16时,双曲线上是否存在一点P,连接,使的面积等于面积?若存在,求出点P的坐标,若不存在,请说明理由.
22.如图,矩形的面积为8,它的边位于x轴上.双曲线经过点A,与矩形的边交于点E,点B在双曲线上,连接并延长交x轴于点F,点G与点О关于点C对称,连接,.
(1)求k的值;
(2)求的面积;
(3)求证:四边形AFGB为平行四边形.
23.如图,直线与反比例函数的图象相交于点,与轴交于点.
(1) 求和的值.
(2) 若点与点关于直线对称,连接.
①求点的坐标;
②若点在反比例函数的图象上,点在轴上,以点为顶点的四边形能否为平行四边形?若能,直接写出点的坐标;若不能,请说明理由.
24.如图,菱形OABC的点B在y轴上,点C坐标为(12,5),双曲线的图象经过点A.
(1) 菱形OABC的边长为____;
(2) 求双曲线的函数关系式;
(3) ①点B关于点O的对称点为D点,过D作直线l垂直于y轴,点P是直线l上一个动点,点E在双曲线上,当P、E、A、B四点构成平行四边形时,求点E的坐标;
②将点P绕点A逆时针旋转90°得点Q,当点Q落在双曲线上时,求点Q的坐标.
答案
一、单选题
1.B 2.D 3.C 4.A 5.A 6.A 7.D 8.A 9.D 10.B
二、填空题
11.1
12.
13.(1)(4,0);(2)4≤t≤或≤t≤-4
14.
15. 4或
16.
17.①②
18.
19.
解:(1)结论:点在反比例函数的图象上,
理由如下:∵反比例函数的图象经过点,点的横坐标是-2,
∴把代入中,得,
∴点的坐标是,
∵点关于坐标原点的对称点为点,
∴点的坐标是,
把代入中,得,
∴点在反比例函数的图象上;
(2)证明:在反比例函数中令x=4则y=-2,
∵过坐标原点作直线交反比例函数的图象于点和点,
∴C,D关于原点对称,
∴C(4,-2),D(-4,2),OC=OD,
∵A,B关于原点对称,
∴OA=OB,
∴四边形ACBD是平行四边形,
∵CD=,AB=,
∴AB=CD,
∴四边形ACBD是矩形;
(3)设点P的坐标为,如图,
当四边形OBP1Q1是菱形时,可得,
∴,解得,
∴P1;
当四边形OBQ2P2是菱形时,可得,
∴,
∴P2;
当四边形OP3BQ3是菱形时,可得,
∴,
解得,
∴P3,
综上所述,满足条件的点的坐标分别为,和.
20.
(1)解:点在这个反比例函数的图像上.
理由如下:
一次函数的图像与反比例函数的图像交于点,
设点的坐标为,
点关于直线的对称点为点,
,平分,
连接交于,如图所示:
,
轴于,
轴,,
,
,
,
在Rt中,,
,
为边上的中线,即,
,
,
,
点在这个反比例函数的图像上;
(2)解:①四边形为正方形,
,垂直平分,
,
设点的坐标为,
,,
,
(负值舍去),
,,
把,代入得,
;
②延长交轴于,如图所示:
,,
点与点关于轴对称,
,则点即为符合条件的点,
由①知,,,
,,
设直线的解析式为,
,解得,
直线的解析式为,
当时,,即,故当最大时,点的坐标为.
21.
(1)解:设点B的坐标为,则点,则:
,
解得(负值已舍去),
故点B的坐标为,
将点B的坐标代入反比例函数表达式得∶,
解得∶;
(2)解:①为直角三角形,理由∶
设点,则点,
∵点A、C的横坐标相同,
∴轴,
∴点B关于y轴的对称点为C,
∴轴,
∴,
∴为直角三角形;
②由①得∶,
则的面积,
解得(负值已舍去),
∴点B的坐标为,C的坐标为,
将点B的坐标代入反比例函数表达式得∶,解得,
∴反比例函数表达式为①;
过点C作直线,交反比例函数于点P,则点P符合题设要求,
同样在AB下方等间隔作直线交反比例函数于点P,则点P也符合要求.
∵,
∴设直线m的表达式为,
将点C的坐标代入,解得,
故直线m的表达式为②,
根据图形的对称性,则直线n的表达式为③,
联立①②并解得∶
或,
联立①③并解得∶
或,
∴点P的坐标为或或或.
22.
(1)解:设,,
根据题意可知:,整理可得:.
(2)解:∵,
∴,
∵点E在,且点B和点E的横坐标相等,
∴,即,
设直线的函数解析式为:,将和代入可得:
,解得:,
故直线的函数解析式为:,
令,可得:,
∴,
∵,即,
∴,
∵点C的横坐标和点B的横坐标相等,
∴,
∴.
证明:∵,点G与点О关于点C对称,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形.
23.
解:(1)将点代入得:,
,
直线的表达式为,
把点代入,得:,
,
将代入得:,
;
①连接,过作轴于,如图:
,
,
是等腰直角三角形,
,
由点与点关于直线对称,知≌,
,即,
,
点的坐标为;
以点为顶点的四边形能为平行四边形,理由如下:
设,又,
Ⅰ若是对角线,则的中点重合,
,
解得,
;
Ⅱ若为对角线,则的中点重合;
,
解得,
;
Ⅲ若为对角线,则的中点重合,
,
解得,
,
综上所述,的坐标为或或.
24.
(1)解:如图所示,连接AC交y轴于J,
∵四边形OABC是菱形,
∴AC⊥OB,AJ=JC,OJ=BJ,
∵点C的坐标为(12,5),
∴AJ=JC=12,OJ=BJ=5,
∴,
故答案为:5;
(2)解:∵AJ=JC=12,OJ=BJ=5,
∴点A的坐标为(-12,5),
∵反比例函数经过点A(-12,5),
∴,
∴,
∴反比例函数解析式为;
(3)解:①设E点坐标为(m,),
∵OJ=BJ=5,
∴OB=10,
∴B点坐标为(0,10),
∵点B关于点O的对称点为D点,
∴D点坐标为(0,-10),
∴直线l为,
设P点坐标为(a,-10)
当AB是以P、E、A、B四点构成平行四边形的对角线时,
∵线段AB与线段PE的中点坐标相同,
∴,
∴,
∴点E的坐标为(,25);
如图所示,当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,
∵与的中点坐标相同,
∴,
∴,
∴的坐标为(12,-5);
同理可以求出当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,点的坐标为(,-15);
综上所述,当E点坐标为(,-5)或(4,-15)或(,25)时,以P、E、A、B四点构成的四边形是平行四边形;
②如图所示,过点A作AT⊥PD于T,过点Q作QR⊥AT于R,
∵点A的坐标为(-12,5),直线l为,
∴AT=15,
∵∠ATP=∠QRA=∠PAQ=90°,
∴∠PAT+∠APT=90°,∠PAT+∠QAR=90°,
∴∠APT=∠QAR,
又∵AP=QA,
∴△APT≌△QRA(AAS),
∴AT=RQ=15,
∴Q点的横坐标为3,
∵Q在反比例函数上,
∴,
∴点Q的坐标为(3,).
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
