浙教版八年级数学 下册试题 《一元二次方程》本章复习题(含答案)
文档属性
| 名称 | 浙教版八年级数学 下册试题 《一元二次方程》本章复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 306.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 08:02:56 | ||
图片预览




文档简介
《一元二次方程》本章复习题
一、单选题
1.若关于的一元二次方程没有实数根,则的值可以是( )
A. B. C.0 D.1
2.已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2,若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )
A.y1=x2+2x和y2=﹣x+1 B.y1=和y2=x+1
C.y1=﹣和y2=﹣x﹣1 D.y1=x2+2x和y2=﹣x﹣1
3.若是方程的两个实数根,则的值为( )
A.3或 B.或9 C.3或 D.或6
4.若关于x的一元二次方程有两个实数根,,且,则( )
A.2或6 B.2或8 C.2 D.6
5.已知关于x的一元二次方程,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
6.关于x的一元二次方程的根的情况,下列说法正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
7.若m、n是一元二次方程x2+3x﹣9=0的两个根,则的值是( )
A.4 B.5 C.6 D.12
8.已知方程的两根分别为,,则的值为( )
A. B. C. D.
9.已知,是方程的两根,则代数式的值是( )
A.-25 B.-24 C.35 D.36
10.在育红学校开展的课外阅读活动中,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x,根据题意,所列方程正确的是( )
A. B.
C. D.
11.定义新运算“※”:对于实数,,,,有,其中等式右边是通常的加法和乘法运算,如:.若关于的方程有两个实数根,则的取值范围是( )
A.且 B. C.且 D.
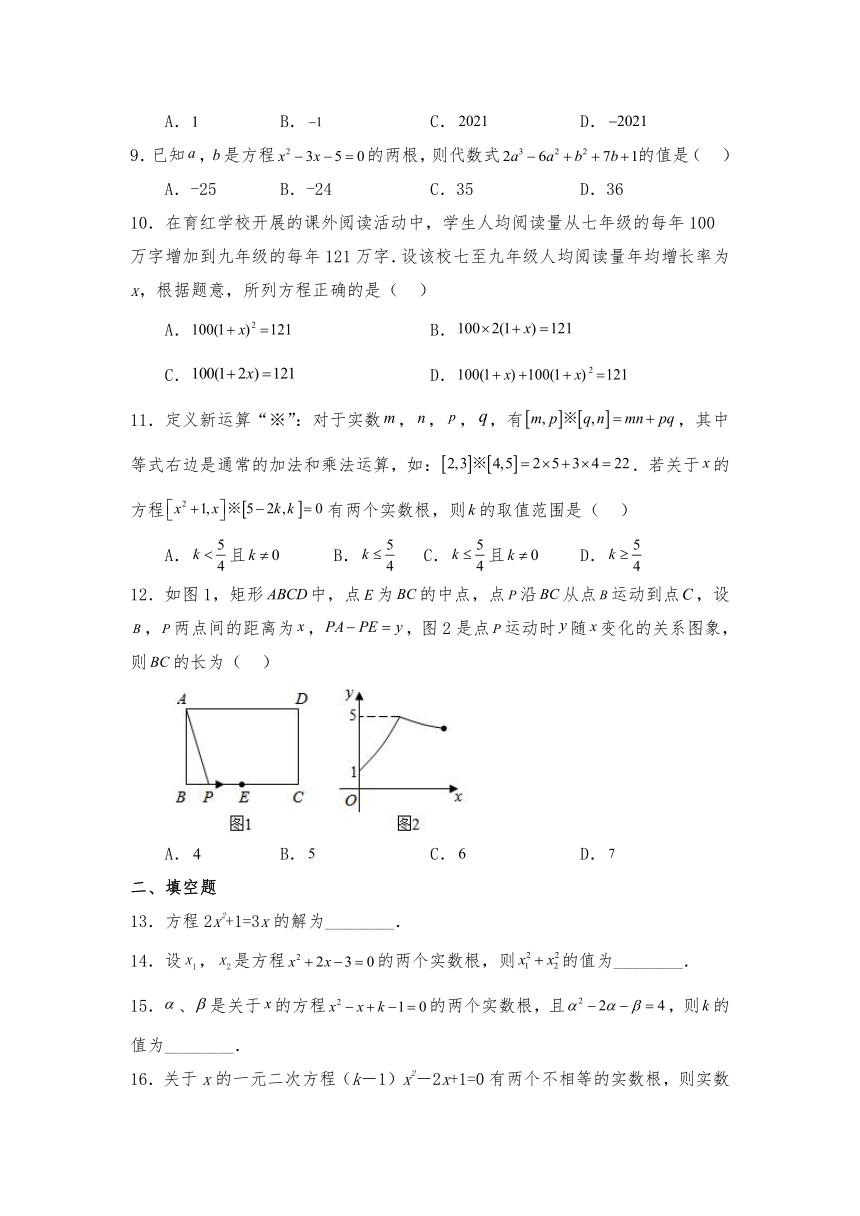
12.如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
A. B. C. D.
二、填空题
13.方程2x2+1=3x的解为________.
14.设,是方程的两个实数根,则的值为________.
15.、是关于的方程的两个实数根,且,则的值为________.
16.关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则实数k的取值范围是_______.
17.已知实数a、b满足a-b2=4,则代数式a2-3b2+a-14的最小值是________.
18.已知x1、x2是关于x的方程x2﹣2x+k﹣1=0的两实数根,且=x12+2x2﹣1,则k的值为 _____.
19.若一个直角三角形两条直角边的长分别是一元二次方程的两个实数根,则这个直角三角形斜边的长是_________.
20.某网络学习平台2022年的新注册用户数为100万,2023年的新注册用户数为169万,设新注册用户数的年平均增长率为x(),则_________(用百分数表示).
21.利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是______.
三、解答题
22.已知关于的一元二次方程.
(1) 求证:方程总有两个不相等的实数根;
(2) 若方程的两个实数根分别为,,且,求的值.
23.已知关于x的一元二次方程有实数根.
(1) 求实数k的取值范围.
(2) 设方程的两个实数根分别为,若,求k的值.
24.如图,在长为50m,宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260m2,道路的宽应为多少?
25.建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.
(1) 求该市改造老旧小区投入资金的年平均增长率;
(2) 2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?
26.某造纸厂为节约木材,实现企业绿色低碳发展,通过技术改造升级,使再生纸项目的生产规模不断扩大.该厂3,4月份共生产再生纸800吨,其中4月份再生纸产量是3月份的2倍少100吨.
(1) 求4月份再生纸的产量;
(2) 若4月份每吨再生纸的利润为1000元,5月份再生纸产量比上月增加.5月份每吨再生纸的利润比上月增加,则5月份再生纸项目月利润达到66万元.求的值;
(3) 若4月份每吨再生纸的利润为1200元,4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同,6月份再生纸项目月利润比上月增加了.求6月份每吨再生纸的利润是多少元?
27.阅读材料:
材料1:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2,则x1+x2=,x1x2=
材料2:已知一元二次方程x2-x-1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵一元二次方程x2-x-1=0的两个实数根分别为m,n,
∴m+n=1,mn=-1,
则m2n+mn2=mn(m+n)=-1×1=-1
根据上述材料,结合你所学的知识,完成下列问题:
材料理解:一元二次方程2x2-3x-1=0的两个根为x1,x2,则x1+x2= ;x1x2= .
类比应用:已知一元二次方程2x2-3x-1=0的两根分别为m、n,求的值.
思维拓展:已知实数s、t满足2s2-3s-1=0,2t2-3t-1=0,且s≠t,求的值.
答案
一、单选题
1.A 2.B 3.A 4.A 5.A 6.A 7.C 8.B 9.D 10.A 11.C 12.C
三、解答题
13.
14.10
15.
16.k<2且k≠1
17.6
18.2
19.
20.30%
21.16
三、解答题
22.
解:(1),
∵,
∴,
该方程总有两个不相等的实数根;
方程的两个实数根,,
由根与系数关系可知,,,
∵,
∴,
∴,
解得:,,
∴,即.
23.
(1)解:∵一元二次方程有实数根.
∴ 0,即32-4(k-2)0,
解得k
(2)∵方程的两个实数根分别为,
∴,
∵,
∴,
∴,
解得k=3.
24.解:设道路的宽应为x米,由题意得
(50-2x)×(38-2x)=1260
解得:x1=4,x2=40(不符合题意,舍去)
答:道路的宽应为4m.
25.
(1)解:设该市改造老旧小区投入资金的年平均增长率为,
根据题意得:,
解这个方程得,,,
经检验,符合本题要求.
答:该市改造老旧小区投入资金的年平均增长率为20%.
(2)设该市在2022年可以改造个老旧小区,
由题意得:,
解得.
∵为正整数,∴最多可以改造18个小区.
答:该市在2022年最多可以改造18个老旧小区.
26.(1)解:设3月份再生纸产量为吨,则4月份的再生纸产量为吨,
由题意得:,
解得:,
∴,
答:4月份再生纸的产量为500吨;
(2)解:由题意得:,
解得:或(不合题意,舍去)
∴,
∴的值20;
(3)解:设4至6月每吨再生纸利润的月平均增长率为,5月份再生纸的产量为吨,
∴
答:6月份每吨再生纸的利润是1500元.
27.
(1)解:∵一元二次方程2x2-3x-1=0的两个根为x1,x2,
∴,.
故答案为:;.
(2)∵一元二次方程2x2-3x-1=0的两根分别为m、n,
∴,,
∴
(3)∵实数s、t满足2s2-3s-1=0,2t2-3t-1=0,
∴s、t可以看作方程2x2-3x-1=0的两个根,
∴,,
∵
∴或,
当时,,
当时,,
综上分析可知,的值为或.
一、单选题
1.若关于的一元二次方程没有实数根,则的值可以是( )
A. B. C.0 D.1
2.已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2,若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )
A.y1=x2+2x和y2=﹣x+1 B.y1=和y2=x+1
C.y1=﹣和y2=﹣x﹣1 D.y1=x2+2x和y2=﹣x﹣1
3.若是方程的两个实数根,则的值为( )
A.3或 B.或9 C.3或 D.或6
4.若关于x的一元二次方程有两个实数根,,且,则( )
A.2或6 B.2或8 C.2 D.6
5.已知关于x的一元二次方程,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
6.关于x的一元二次方程的根的情况,下列说法正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
7.若m、n是一元二次方程x2+3x﹣9=0的两个根,则的值是( )
A.4 B.5 C.6 D.12
8.已知方程的两根分别为,,则的值为( )
A. B. C. D.
9.已知,是方程的两根,则代数式的值是( )
A.-25 B.-24 C.35 D.36
10.在育红学校开展的课外阅读活动中,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x,根据题意,所列方程正确的是( )
A. B.
C. D.
11.定义新运算“※”:对于实数,,,,有,其中等式右边是通常的加法和乘法运算,如:.若关于的方程有两个实数根,则的取值范围是( )
A.且 B. C.且 D.
12.如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
A. B. C. D.
二、填空题
13.方程2x2+1=3x的解为________.
14.设,是方程的两个实数根,则的值为________.
15.、是关于的方程的两个实数根,且,则的值为________.
16.关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则实数k的取值范围是_______.
17.已知实数a、b满足a-b2=4,则代数式a2-3b2+a-14的最小值是________.
18.已知x1、x2是关于x的方程x2﹣2x+k﹣1=0的两实数根,且=x12+2x2﹣1,则k的值为 _____.
19.若一个直角三角形两条直角边的长分别是一元二次方程的两个实数根,则这个直角三角形斜边的长是_________.
20.某网络学习平台2022年的新注册用户数为100万,2023年的新注册用户数为169万,设新注册用户数的年平均增长率为x(),则_________(用百分数表示).
21.利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是______.
三、解答题
22.已知关于的一元二次方程.
(1) 求证:方程总有两个不相等的实数根;
(2) 若方程的两个实数根分别为,,且,求的值.
23.已知关于x的一元二次方程有实数根.
(1) 求实数k的取值范围.
(2) 设方程的两个实数根分别为,若,求k的值.
24.如图,在长为50m,宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260m2,道路的宽应为多少?
25.建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.
(1) 求该市改造老旧小区投入资金的年平均增长率;
(2) 2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?
26.某造纸厂为节约木材,实现企业绿色低碳发展,通过技术改造升级,使再生纸项目的生产规模不断扩大.该厂3,4月份共生产再生纸800吨,其中4月份再生纸产量是3月份的2倍少100吨.
(1) 求4月份再生纸的产量;
(2) 若4月份每吨再生纸的利润为1000元,5月份再生纸产量比上月增加.5月份每吨再生纸的利润比上月增加,则5月份再生纸项目月利润达到66万元.求的值;
(3) 若4月份每吨再生纸的利润为1200元,4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同,6月份再生纸项目月利润比上月增加了.求6月份每吨再生纸的利润是多少元?
27.阅读材料:
材料1:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2,则x1+x2=,x1x2=
材料2:已知一元二次方程x2-x-1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵一元二次方程x2-x-1=0的两个实数根分别为m,n,
∴m+n=1,mn=-1,
则m2n+mn2=mn(m+n)=-1×1=-1
根据上述材料,结合你所学的知识,完成下列问题:
材料理解:一元二次方程2x2-3x-1=0的两个根为x1,x2,则x1+x2= ;x1x2= .
类比应用:已知一元二次方程2x2-3x-1=0的两根分别为m、n,求的值.
思维拓展:已知实数s、t满足2s2-3s-1=0,2t2-3t-1=0,且s≠t,求的值.
答案
一、单选题
1.A 2.B 3.A 4.A 5.A 6.A 7.C 8.B 9.D 10.A 11.C 12.C
三、解答题
13.
14.10
15.
16.k<2且k≠1
17.6
18.2
19.
20.30%
21.16
三、解答题
22.
解:(1),
∵,
∴,
该方程总有两个不相等的实数根;
方程的两个实数根,,
由根与系数关系可知,,,
∵,
∴,
∴,
解得:,,
∴,即.
23.
(1)解:∵一元二次方程有实数根.
∴ 0,即32-4(k-2)0,
解得k
(2)∵方程的两个实数根分别为,
∴,
∵,
∴,
∴,
解得k=3.
24.解:设道路的宽应为x米,由题意得
(50-2x)×(38-2x)=1260
解得:x1=4,x2=40(不符合题意,舍去)
答:道路的宽应为4m.
25.
(1)解:设该市改造老旧小区投入资金的年平均增长率为,
根据题意得:,
解这个方程得,,,
经检验,符合本题要求.
答:该市改造老旧小区投入资金的年平均增长率为20%.
(2)设该市在2022年可以改造个老旧小区,
由题意得:,
解得.
∵为正整数,∴最多可以改造18个小区.
答:该市在2022年最多可以改造18个老旧小区.
26.(1)解:设3月份再生纸产量为吨,则4月份的再生纸产量为吨,
由题意得:,
解得:,
∴,
答:4月份再生纸的产量为500吨;
(2)解:由题意得:,
解得:或(不合题意,舍去)
∴,
∴的值20;
(3)解:设4至6月每吨再生纸利润的月平均增长率为,5月份再生纸的产量为吨,
∴
答:6月份每吨再生纸的利润是1500元.
27.
(1)解:∵一元二次方程2x2-3x-1=0的两个根为x1,x2,
∴,.
故答案为:;.
(2)∵一元二次方程2x2-3x-1=0的两根分别为m、n,
∴,,
∴
(3)∵实数s、t满足2s2-3s-1=0,2t2-3t-1=0,
∴s、t可以看作方程2x2-3x-1=0的两个根,
∴,,
∵
∴或,
当时,,
当时,,
综上分析可知,的值为或.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
