浙教版九年级数学上册第2章 简单的概率事件 单元复习题(含解析)
文档属性
| 名称 | 浙教版九年级数学上册第2章 简单的概率事件 单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 356.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 11:26:15 | ||
图片预览




文档简介
浙教版九年级数学上册第2章简单的概率事件单元复习题
一、单选题
1.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. B. C. D.
2.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( ).
A. B. C. D.
3.中国古代数学有着辉煌的成就,《周牌算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献.某中学拟从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是( )
A. B. C. D.
4.下列说法错误的是( )
A.“从一个只有红球的袋子里面摸出一个球是红球”是必然事件
B.如果明天降水的概率是,那么明天有半天都在降雨
C.“随意掷两个均匀的骰子,朝上面的点数之和为13”是不可能事件
D.随机事件发生的概率介于和之间
5.盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同.从中任意拿出一支笔芯,则拿出黑色笔芯的概率是( )
A. B. C. D.
6.不透明的袋子里有50张2022年北京冬奥会宣传卡片,每张卡片正面印有会徽吉祥物冰墩墩、吉祥物雪容融三种图案中的一种,卡片背面完全相同且不透明.印有冰墩墩的卡片共有n张,若从袋子里随机摸出1张卡片,印有冰图案的概率是,则n=( )
A.25 B.10 C.5 D.1
7.下列事件中,不确定事件是( )
A.三角形的三个内角和等于 180 度
B.同位角相等
C.三角形的三条角平分线一定交于一点
D.对顶角相等
8.一个不透明的盒子里装有除颜色外其他都相同的四个球,其中1个白球、1个黑球、2个红球,搅匀后随机从盒子中摸出两个球,则摸出1个白球的概率是( )
A. B. C. D.
9.100个白色乒乓球中有20个被染红,随机抽取20个球,下列结论正确的是( )
A.红球一定刚好4个 B.红球不可能少于4个
C.红球可能多于4个 D.抽到的白球一定比红球多
10. 八卦图是中国古老的科学文化遗产,是我国古代劳动人民智慧的结晶,古人认为,世间万物皆可分类归至八卦之中,相传,德国数学家莱布尼茨受八卦图的启发而发明了电子计算机使用的二进制.八卦图中的每一卦由三根线组成.如果从图中任选一卦,那么这一卦中恰有根“”和根“”的概率是( )
A. B. C. D.
二、填空题
11.单项选择题是数学试题的重要组成部分,当你遇到不懂做的情况时,如果你随便选一个答案(假设每个题目有4个备选答案),那么你答对的可能性为 .
12.同时掷两个质地均匀的六面体骰子,两个骰子向上一面点数相同的概率是
13.在平面直角坐标系中有五个点,分别是,,,,,从中任选一个点恰好在第一象限的概率是 .
14.小明制作了5张卡片,上面分别写了一个条件:①;②;③;④;⑤.从中随机抽取一张卡片,能判定是菱形的概率是 .
三、解答题
15.中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是多少?
16.一对姐弟中只能有一人参加夏季夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.试用列表法或树状图分析这种方法对姐弟俩是否公平.
17.某市体育中考现场考试内容有三项:50米跑为必测项目;另外在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.假设每名考生在两项选择项目中任意各选一项,有多少种不同的选择方案?它们都是什么事件?
18.小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 7 9 6 8 20 10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验得出,出现5点朝上的机会最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
19.甲、乙、丙、丁四位同学参加校田径运动会4X100米接力跑比赛,因为丁的速度最快,所以由他负责跑最后一棒,其他三位同学的跑步顺序随机安排。
(1)请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序;
(2)请求出正好由丙将接力棒交给丁的概率。
20.甲、乙两人玩“锤子、石头、剪子、布”游戏.他们在不透明的袋子中放入形状、大小均相同的19张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为3、4、5、7,两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
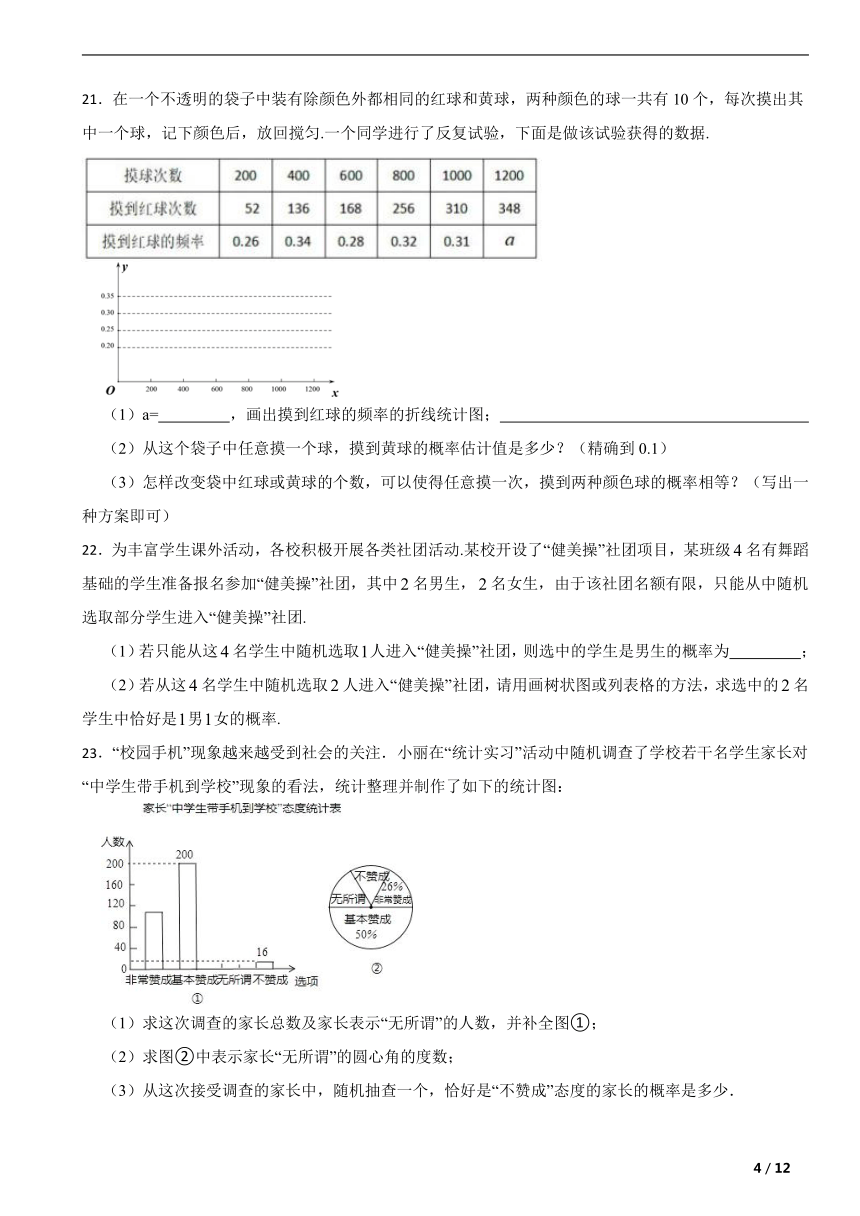
21.在一个不透明的袋子中装有除颜色外都相同的红球和黄球,两种颜色的球一共有10个,每次摸出其中一个球,记下颜色后,放回搅匀.一个同学进行了反复试验,下面是做该试验获得的数据.
(1)a= ,画出摸到红球的频率的折线统计图;
(2)从这个袋子中任意摸一个球,摸到黄球的概率估计值是多少?(精确到0.1)
(3)怎样改变袋中红球或黄球的个数,可以使得任意摸一次,摸到两种颜色球的概率相等?(写出一种方案即可)
22.为丰富学生课外活动,各校积极开展各类社团活动.某校开设了“健美操”社团项目,某班级名有舞蹈基础的学生准备报名参加“健美操”社团,其中名男生,名女生,由于该社团名额有限,只能从中随机选取部分学生进入“健美操”社团.
(1)若只能从这名学生中随机选取人进入“健美操”社团,则选中的学生是男生的概率为 ;
(2)若从这名学生中随机选取人进入“健美操”社团,请用画树状图或列表格的方法,求选中的名学生中恰好是男女的概率.
23.“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
答案解析部分
1.【答案】C
【解析】【解答】解:将方格纸中, 随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5中等可能结果,与图中阴影部分构成轴对称图形有②④⑤3种,
∴P(
与图中阴影部分构成轴对称图形)=
.
故答案为:C.
【分析】根据随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5中等可能结果,与图中阴影部分构成轴对称图形有3种,利用概率公式计算即可.
2.【答案】B
【解析】【解答】列表得:
1 2 3 4
1 - 2+1=3 3+1=4 4+1=5
2 1+2=3 - 3+2=5 4+2=6
3 1+3=4 2+3=5 - 4+3=7
4 1+4=5 2+4=6 3+4=7 -
∵共有12种等可能的结果,这两个乒乓球上的数字之和大于5的有4种情况,
∴这两个乒乓球上的数字之和大于5的概率为: .故选B.
【分析】此题考查了列表法与树状图法求概率的知识.注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
首先根据题意列出表格,然后由表格求得所有等可能的与这两个乒乓球上的数字之和大于5的情况,然后利用概率公式求解即可求得答案.
3.【答案】A
【解析】【解答】 《周牌算经》《算学启蒙》《测圆海镜》《四元玉鉴》 共4本,
所有可能的结果有4种,且每种结果出现的可能性相等,故恰好选中《算学启蒙》的概率是
故答案为:A
【分析】本题考查概率的计算。熟练掌握概率公式是解题关键。
4.【答案】B
【解析】【解答】解:A、“从一个只有红球的袋子里面摸出一个球是红球”是必然事件,A不符合题意;
B、如果明天降水的概率是,那么明天不一定有半天都在降雨,B符合题意;
C、画树状图如下:
共有36种等可能的结果,其中朝上面的点数之和为13的结果不存在,
“随意掷两个均匀的骰子,朝上面的点数之和为13”是不可能事件,C不符合题意;
D、随机事件发生的概率介于0和1之间,D不符合题意;
故答案为:B.
【分析】根据必然事件、随机事件、不可能事件的定义逐项判断即可。
5.【答案】C
【解析】【解答】解:因为全部是5支笔,2支黑色笔芯,所以从中任意拿出一支笔芯,拿出黑色笔芯的概率是 。
故答案为:C。
【分析】 盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同,从中任意拿出一支笔芯,共有5种等可能的结果,则拿出黑色笔芯的只有2种等可能的结果,根据概率公式即可算出拿出黑色笔芯的概率 。
6.【答案】B
【解析】【解答】解:由题意得,
,
解得
.
故答案为:B.
【分析】根据概率公式列出方程
,求出n的值即可。
7.【答案】B
【解析】【解答】解:A、是必然事件,不符合题意;
B、是不确定事件,符合题意;
C、是必然事件,不符合题意;
D、是必然事件,不符合题意.
故答案为:B.
【分析】不确定事件就是可能发生也可能不发生的事件,依据定义即可判断。
8.【答案】A
【解析】【解答】解:画树状图得:
因为共有12种等可能的结果,其中摸到的两个球有1个白球的有6种情况,
所以摸出1个白球的概率是 .
故答案为:A.
【分析】先根据题意画出树状图,然后由树状图求得所有等可能的结果与摸到的两个球有1个白球的情况,再利用概率公式计算即可.
9.【答案】C
【解析】【解答】解:由题意得,抽到的红球的数量可能为20×=4个,
所以,抽到的红球可能是4个,也可能多于4个或少于4个,
说法“红球一定刚好4个”,“红球不可能少于4个”,“抽到的白球一定比红球多”都过于武断,不正确.
故选C.
【分析】根据被染红的球的可能性求出抽取的红球的可能数量,再对各选项判断即可得解.
10.【答案】C
【解析】【解答】解:由题意可得:
共有8中等可能的结果,其中恰有根“”和根“”的有3中结果
则概率为:
故答案为:C
【分析】根据简单事件的概率进行计算即可。
11.【答案】
【解析】【解答】解:根据题意,每个题目有4个备选答案,而只有一个是正确的,
故答对的可能性为 .
故答案为: .
【分析】这个实验有4个出现机会相同的结果,而正确的只有1个,根据概率公式即可求解
12.【答案】
【解析】【解答】列表得:
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
∴一共有36种情况,两个骰子点数相同为(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种可能.
∴两个骰子点数相同的概率是 .
【分析】若第一个骰子出现的点数是1,第二个骰子出现的点数就有6种结果,所以所有可能的结果有66=36种,而两个骰子点数相同的有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)共6种可能则两个骰子点数相同的概率==.
13.【答案】
【解析】【解答】∵从中任选一个点共有5种等可能情况,在第一象限的点有A和D两种,
∴P(任选一个点恰好在第一象限)=,
故答案为:.
【分析】利用概率公式求解即可。
14.【答案】
【解析】【解答】解:根据菱形的判断,可得①;④能判定平行四边形ABCD是菱形,
∴能判定是菱形的概率是,
故答案为:.
【分析】根据菱形的判定方法一一判断即可。
15.【答案】解:∵20个商标中2个已翻出,还剩18张,18张中还有3张有奖的,
∴第三次翻牌获奖的概率是:
【解析】【分析】先求出20个商标中还剩的张数,再求出其中有奖的张数,最后根据概率公式进行计算即可.
16.【答案】解:画树状图得:
∵共有16种等可能的结果,抽取的两张卡片上的数字之和是5的倍数有4种情况,抽取的两张卡片上的数字之和是3的倍数有5中情况,
∴P(姐姐参加)==,P(弟弟参加)=,
∴不公平.
【解析】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果以及抽取的两张卡片上的数字之和是5的倍数的情况与抽取的两张卡片上的数字之和是3的倍数的情况,再利用概率公式求得其概率,比较概率的大小,即可知这种方法对姐弟俩是否公平.
17.【答案】解:每位考生可选择:①50米跑、立定跳远、坐位体前屈;②50米跑、实心球、坐位体前屈;③50米跑、立定跳远、1分钟跳绳;④50米跑、实心球、1分钟跳绳;共有4种选择方案;
它们都是随机事件.
【解析】【分析】 根据列举可得每位考生可选择的方案共有4种;根据在一定条件下,可能发生也可能不发生的事件,称为随机事件;即可判断出结论.
18.【答案】解:(1)3点朝上的频率为=;
5点朝上的频率为=;
(2)小颖和小红说法都错,因为实验是随机的,不能反映事物的概率.
【解析】【分析】(1)根据概率的公式计算“3点朝上”的频率和“5点朝上”的频率;
(2)根据随机事件的性质回答.
19.【答案】(1)画树状图为:
(2)根据树状图可得共有24种等可能的情况,恰好由丙将接力棒交给丁的有甲乙丙丁、甲丙丁乙、乙甲丙丁、乙丙丁甲、丙丁乙甲、丙丁甲乙6种情况,
∴恰好由 丙将接力棒交给丁的概率是.
【解析】【分析】 (1)根据树状图列举出所有情况即可;
(2)看恰好由甲将接力棒交给乙的情况数占总情况数的多少即可.
20.【答案】(1)解:P(甲摸石头)=
(2)解:P(乙胜)=
(3)解:P(甲摸锤子胜)= ,
P(甲摸石头胜)= ,
P(甲摸剪子胜)= ,P
(甲摸布胜)= ,
,
∴甲摸锤子获胜的可能性最大.
【解析】【分析】(1)共有19张牌,石头的有4张,利用概率公式计算即可;
(2)甲先摸出“石头”后,还有18张牌,而布有7种情况,利用概率公式求解即可;
(3)分别算出各种卡片获胜占总情况的多少,比较即可得出答案。
21.【答案】(1)0.29;摸到红球的频率的折线统计图如图所示:
(2)解:由题意得:摸到红球概率的估计值为0.3,所以摸到黄球的概率估计值=1-0.3=0.7
(3)解:由于袋子中有红球3个,黄球7个,可设添加x个红球,则 ,解得:x=4;
或设拿走y个黄球,则 ,解得:y=4.
所以添加4个红球或拿掉4个黄球(答案不唯一),可以使得任意摸一次,摸到两种颜色球的概率相等.
【解析】【解答】解:(1)348÷1200=0.29,即 ;
摸到红球的频率的折线统计图如图所示:
【分析】(1)根据题意只要用348除以1200即得a的值,进而可画出摸到红球的频率的折线统计图;(2)由表格数据可得摸到红球概率的估计值,进而可得摸到黄球的概率估计值;
(3)先由前面确定袋子中红球和黄球的个数,再设添加x个红球或拿走y个黄球,根据题意列出方程,解方程即可得出结论.
22.【答案】(1)
(2)解:画树状图如下:
由图可知,共有种可能的结果,其中恰为男女的结果出现次,
则选取的名学生恰为男女的概率为.
【解析】【解答】解:(1)从这名学生中随机选取人进入“健美操”社团,则选中的学生是男生的概率为,
故答案为:;
【分析】(1)利用男生的人数除以总人数即可;
(2)画出树状图,找出总情况数以及1男1女的情况数,然后根据概率公式进行计算.
23.【答案】(1)解:家长总数:200÷50%=400名,
表示“无所谓”人数:400﹣200﹣16﹣400×26%=80名,补全图①,
(2)解:80÷400×360°=72°
(3)解:16÷400=
【解析】【分析】(1)由图象可以得出基本赞成的有200人占50%,可以求出总数,由总数可以求出非常赞成的人数和无所谓的人数.(2)由(1)的总数求出无所谓的百分比再乘以360°就可以求出圆心角的度数.(3)这次受调查的家长不赞成的人数除以总数就是抽到恰好是“不赞成”态度的家长的概率.
1 / 1
一、单选题
1.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. B. C. D.
2.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( ).
A. B. C. D.
3.中国古代数学有着辉煌的成就,《周牌算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献.某中学拟从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是( )
A. B. C. D.
4.下列说法错误的是( )
A.“从一个只有红球的袋子里面摸出一个球是红球”是必然事件
B.如果明天降水的概率是,那么明天有半天都在降雨
C.“随意掷两个均匀的骰子,朝上面的点数之和为13”是不可能事件
D.随机事件发生的概率介于和之间
5.盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同.从中任意拿出一支笔芯,则拿出黑色笔芯的概率是( )
A. B. C. D.
6.不透明的袋子里有50张2022年北京冬奥会宣传卡片,每张卡片正面印有会徽吉祥物冰墩墩、吉祥物雪容融三种图案中的一种,卡片背面完全相同且不透明.印有冰墩墩的卡片共有n张,若从袋子里随机摸出1张卡片,印有冰图案的概率是,则n=( )
A.25 B.10 C.5 D.1
7.下列事件中,不确定事件是( )
A.三角形的三个内角和等于 180 度
B.同位角相等
C.三角形的三条角平分线一定交于一点
D.对顶角相等
8.一个不透明的盒子里装有除颜色外其他都相同的四个球,其中1个白球、1个黑球、2个红球,搅匀后随机从盒子中摸出两个球,则摸出1个白球的概率是( )
A. B. C. D.
9.100个白色乒乓球中有20个被染红,随机抽取20个球,下列结论正确的是( )
A.红球一定刚好4个 B.红球不可能少于4个
C.红球可能多于4个 D.抽到的白球一定比红球多
10. 八卦图是中国古老的科学文化遗产,是我国古代劳动人民智慧的结晶,古人认为,世间万物皆可分类归至八卦之中,相传,德国数学家莱布尼茨受八卦图的启发而发明了电子计算机使用的二进制.八卦图中的每一卦由三根线组成.如果从图中任选一卦,那么这一卦中恰有根“”和根“”的概率是( )
A. B. C. D.
二、填空题
11.单项选择题是数学试题的重要组成部分,当你遇到不懂做的情况时,如果你随便选一个答案(假设每个题目有4个备选答案),那么你答对的可能性为 .
12.同时掷两个质地均匀的六面体骰子,两个骰子向上一面点数相同的概率是
13.在平面直角坐标系中有五个点,分别是,,,,,从中任选一个点恰好在第一象限的概率是 .
14.小明制作了5张卡片,上面分别写了一个条件:①;②;③;④;⑤.从中随机抽取一张卡片,能判定是菱形的概率是 .
三、解答题
15.中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是多少?
16.一对姐弟中只能有一人参加夏季夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.试用列表法或树状图分析这种方法对姐弟俩是否公平.
17.某市体育中考现场考试内容有三项:50米跑为必测项目;另外在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.假设每名考生在两项选择项目中任意各选一项,有多少种不同的选择方案?它们都是什么事件?
18.小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 7 9 6 8 20 10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验得出,出现5点朝上的机会最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
19.甲、乙、丙、丁四位同学参加校田径运动会4X100米接力跑比赛,因为丁的速度最快,所以由他负责跑最后一棒,其他三位同学的跑步顺序随机安排。
(1)请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序;
(2)请求出正好由丙将接力棒交给丁的概率。
20.甲、乙两人玩“锤子、石头、剪子、布”游戏.他们在不透明的袋子中放入形状、大小均相同的19张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为3、4、5、7,两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
21.在一个不透明的袋子中装有除颜色外都相同的红球和黄球,两种颜色的球一共有10个,每次摸出其中一个球,记下颜色后,放回搅匀.一个同学进行了反复试验,下面是做该试验获得的数据.
(1)a= ,画出摸到红球的频率的折线统计图;
(2)从这个袋子中任意摸一个球,摸到黄球的概率估计值是多少?(精确到0.1)
(3)怎样改变袋中红球或黄球的个数,可以使得任意摸一次,摸到两种颜色球的概率相等?(写出一种方案即可)
22.为丰富学生课外活动,各校积极开展各类社团活动.某校开设了“健美操”社团项目,某班级名有舞蹈基础的学生准备报名参加“健美操”社团,其中名男生,名女生,由于该社团名额有限,只能从中随机选取部分学生进入“健美操”社团.
(1)若只能从这名学生中随机选取人进入“健美操”社团,则选中的学生是男生的概率为 ;
(2)若从这名学生中随机选取人进入“健美操”社团,请用画树状图或列表格的方法,求选中的名学生中恰好是男女的概率.
23.“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
答案解析部分
1.【答案】C
【解析】【解答】解:将方格纸中, 随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5中等可能结果,与图中阴影部分构成轴对称图形有②④⑤3种,
∴P(
与图中阴影部分构成轴对称图形)=
.
故答案为:C.
【分析】根据随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5中等可能结果,与图中阴影部分构成轴对称图形有3种,利用概率公式计算即可.
2.【答案】B
【解析】【解答】列表得:
1 2 3 4
1 - 2+1=3 3+1=4 4+1=5
2 1+2=3 - 3+2=5 4+2=6
3 1+3=4 2+3=5 - 4+3=7
4 1+4=5 2+4=6 3+4=7 -
∵共有12种等可能的结果,这两个乒乓球上的数字之和大于5的有4种情况,
∴这两个乒乓球上的数字之和大于5的概率为: .故选B.
【分析】此题考查了列表法与树状图法求概率的知识.注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
首先根据题意列出表格,然后由表格求得所有等可能的与这两个乒乓球上的数字之和大于5的情况,然后利用概率公式求解即可求得答案.
3.【答案】A
【解析】【解答】 《周牌算经》《算学启蒙》《测圆海镜》《四元玉鉴》 共4本,
所有可能的结果有4种,且每种结果出现的可能性相等,故恰好选中《算学启蒙》的概率是
故答案为:A
【分析】本题考查概率的计算。熟练掌握概率公式是解题关键。
4.【答案】B
【解析】【解答】解:A、“从一个只有红球的袋子里面摸出一个球是红球”是必然事件,A不符合题意;
B、如果明天降水的概率是,那么明天不一定有半天都在降雨,B符合题意;
C、画树状图如下:
共有36种等可能的结果,其中朝上面的点数之和为13的结果不存在,
“随意掷两个均匀的骰子,朝上面的点数之和为13”是不可能事件,C不符合题意;
D、随机事件发生的概率介于0和1之间,D不符合题意;
故答案为:B.
【分析】根据必然事件、随机事件、不可能事件的定义逐项判断即可。
5.【答案】C
【解析】【解答】解:因为全部是5支笔,2支黑色笔芯,所以从中任意拿出一支笔芯,拿出黑色笔芯的概率是 。
故答案为:C。
【分析】 盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同,从中任意拿出一支笔芯,共有5种等可能的结果,则拿出黑色笔芯的只有2种等可能的结果,根据概率公式即可算出拿出黑色笔芯的概率 。
6.【答案】B
【解析】【解答】解:由题意得,
,
解得
.
故答案为:B.
【分析】根据概率公式列出方程
,求出n的值即可。
7.【答案】B
【解析】【解答】解:A、是必然事件,不符合题意;
B、是不确定事件,符合题意;
C、是必然事件,不符合题意;
D、是必然事件,不符合题意.
故答案为:B.
【分析】不确定事件就是可能发生也可能不发生的事件,依据定义即可判断。
8.【答案】A
【解析】【解答】解:画树状图得:
因为共有12种等可能的结果,其中摸到的两个球有1个白球的有6种情况,
所以摸出1个白球的概率是 .
故答案为:A.
【分析】先根据题意画出树状图,然后由树状图求得所有等可能的结果与摸到的两个球有1个白球的情况,再利用概率公式计算即可.
9.【答案】C
【解析】【解答】解:由题意得,抽到的红球的数量可能为20×=4个,
所以,抽到的红球可能是4个,也可能多于4个或少于4个,
说法“红球一定刚好4个”,“红球不可能少于4个”,“抽到的白球一定比红球多”都过于武断,不正确.
故选C.
【分析】根据被染红的球的可能性求出抽取的红球的可能数量,再对各选项判断即可得解.
10.【答案】C
【解析】【解答】解:由题意可得:
共有8中等可能的结果,其中恰有根“”和根“”的有3中结果
则概率为:
故答案为:C
【分析】根据简单事件的概率进行计算即可。
11.【答案】
【解析】【解答】解:根据题意,每个题目有4个备选答案,而只有一个是正确的,
故答对的可能性为 .
故答案为: .
【分析】这个实验有4个出现机会相同的结果,而正确的只有1个,根据概率公式即可求解
12.【答案】
【解析】【解答】列表得:
(1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
(1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
(1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
(1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
(1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
(1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
∴一共有36种情况,两个骰子点数相同为(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种可能.
∴两个骰子点数相同的概率是 .
【分析】若第一个骰子出现的点数是1,第二个骰子出现的点数就有6种结果,所以所有可能的结果有66=36种,而两个骰子点数相同的有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)共6种可能则两个骰子点数相同的概率==.
13.【答案】
【解析】【解答】∵从中任选一个点共有5种等可能情况,在第一象限的点有A和D两种,
∴P(任选一个点恰好在第一象限)=,
故答案为:.
【分析】利用概率公式求解即可。
14.【答案】
【解析】【解答】解:根据菱形的判断,可得①;④能判定平行四边形ABCD是菱形,
∴能判定是菱形的概率是,
故答案为:.
【分析】根据菱形的判定方法一一判断即可。
15.【答案】解:∵20个商标中2个已翻出,还剩18张,18张中还有3张有奖的,
∴第三次翻牌获奖的概率是:
【解析】【分析】先求出20个商标中还剩的张数,再求出其中有奖的张数,最后根据概率公式进行计算即可.
16.【答案】解:画树状图得:
∵共有16种等可能的结果,抽取的两张卡片上的数字之和是5的倍数有4种情况,抽取的两张卡片上的数字之和是3的倍数有5中情况,
∴P(姐姐参加)==,P(弟弟参加)=,
∴不公平.
【解析】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果以及抽取的两张卡片上的数字之和是5的倍数的情况与抽取的两张卡片上的数字之和是3的倍数的情况,再利用概率公式求得其概率,比较概率的大小,即可知这种方法对姐弟俩是否公平.
17.【答案】解:每位考生可选择:①50米跑、立定跳远、坐位体前屈;②50米跑、实心球、坐位体前屈;③50米跑、立定跳远、1分钟跳绳;④50米跑、实心球、1分钟跳绳;共有4种选择方案;
它们都是随机事件.
【解析】【分析】 根据列举可得每位考生可选择的方案共有4种;根据在一定条件下,可能发生也可能不发生的事件,称为随机事件;即可判断出结论.
18.【答案】解:(1)3点朝上的频率为=;
5点朝上的频率为=;
(2)小颖和小红说法都错,因为实验是随机的,不能反映事物的概率.
【解析】【分析】(1)根据概率的公式计算“3点朝上”的频率和“5点朝上”的频率;
(2)根据随机事件的性质回答.
19.【答案】(1)画树状图为:
(2)根据树状图可得共有24种等可能的情况,恰好由丙将接力棒交给丁的有甲乙丙丁、甲丙丁乙、乙甲丙丁、乙丙丁甲、丙丁乙甲、丙丁甲乙6种情况,
∴恰好由 丙将接力棒交给丁的概率是.
【解析】【分析】 (1)根据树状图列举出所有情况即可;
(2)看恰好由甲将接力棒交给乙的情况数占总情况数的多少即可.
20.【答案】(1)解:P(甲摸石头)=
(2)解:P(乙胜)=
(3)解:P(甲摸锤子胜)= ,
P(甲摸石头胜)= ,
P(甲摸剪子胜)= ,P
(甲摸布胜)= ,
,
∴甲摸锤子获胜的可能性最大.
【解析】【分析】(1)共有19张牌,石头的有4张,利用概率公式计算即可;
(2)甲先摸出“石头”后,还有18张牌,而布有7种情况,利用概率公式求解即可;
(3)分别算出各种卡片获胜占总情况的多少,比较即可得出答案。
21.【答案】(1)0.29;摸到红球的频率的折线统计图如图所示:
(2)解:由题意得:摸到红球概率的估计值为0.3,所以摸到黄球的概率估计值=1-0.3=0.7
(3)解:由于袋子中有红球3个,黄球7个,可设添加x个红球,则 ,解得:x=4;
或设拿走y个黄球,则 ,解得:y=4.
所以添加4个红球或拿掉4个黄球(答案不唯一),可以使得任意摸一次,摸到两种颜色球的概率相等.
【解析】【解答】解:(1)348÷1200=0.29,即 ;
摸到红球的频率的折线统计图如图所示:
【分析】(1)根据题意只要用348除以1200即得a的值,进而可画出摸到红球的频率的折线统计图;(2)由表格数据可得摸到红球概率的估计值,进而可得摸到黄球的概率估计值;
(3)先由前面确定袋子中红球和黄球的个数,再设添加x个红球或拿走y个黄球,根据题意列出方程,解方程即可得出结论.
22.【答案】(1)
(2)解:画树状图如下:
由图可知,共有种可能的结果,其中恰为男女的结果出现次,
则选取的名学生恰为男女的概率为.
【解析】【解答】解:(1)从这名学生中随机选取人进入“健美操”社团,则选中的学生是男生的概率为,
故答案为:;
【分析】(1)利用男生的人数除以总人数即可;
(2)画出树状图,找出总情况数以及1男1女的情况数,然后根据概率公式进行计算.
23.【答案】(1)解:家长总数:200÷50%=400名,
表示“无所谓”人数:400﹣200﹣16﹣400×26%=80名,补全图①,
(2)解:80÷400×360°=72°
(3)解:16÷400=
【解析】【分析】(1)由图象可以得出基本赞成的有200人占50%,可以求出总数,由总数可以求出非常赞成的人数和无所谓的人数.(2)由(1)的总数求出无所谓的百分比再乘以360°就可以求出圆心角的度数.(3)这次受调查的家长不赞成的人数除以总数就是抽到恰好是“不赞成”态度的家长的概率.
1 / 1
同课章节目录
