浙教版数学2015-2016学年八年级上册“单元精品卷”第1章 三角形的初步知识(基础检测卷) 含精析
文档属性
| 名称 | 浙教版数学2015-2016学年八年级上册“单元精品卷”第1章 三角形的初步知识(基础检测卷) 含精析 |  | |
| 格式 | zip | ||
| 文件大小 | 172.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-30 19:40:56 | ||
图片预览


文档简介
2015年浙教版数学八年级上册“单元精品卷”(含精析)
第1章 三角形的初步知识 (基础检测卷)
题 型
选择题
填空题
解答题
总 分
得 分
一、选择题。(本题有10个小题,每小题3分,共30分)
1.有长为、、、的四根木棒,选其中的根作为三角形的边,可以围成的三角形的个数是( )www.21-cn-jy.com
A.1个 B.2个 C.3个 D.4个
2.一个三角形的三条边长分别为1、2、x,则x的取值范围是( )
A、1≤x≤3 B、1<x≤3 C、1≤x<3 D、1<x<3
3.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A.60° B.70° C.80° D.90
4.下列命题是真命题的是( )
A.同旁内角互补 B.垂直于同一条直线的两直线平行
C.邻补角相等 D.两直线平行,内错角相等
5.某学生在暑假期间观察了x天的天气情况,其结果是:①共有7天上午是晴天;②共有5天下午是晴天;③共下了8次雨;④下午下雨的那天,上午是晴天.则x=( )
A.8 B.9 C.10 D.11
6.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.AAS D.ASA
7.用两个全等的直角三角形拼下列图形:①平行四边形;②矩形;③梯形;④正方形;⑤等腰三角形;⑥等边三角形;可以拼成的图形是 ( )21世纪教育网版权所有
A、①④⑤ B、②⑤⑥ C、①②③ D、①②⑤
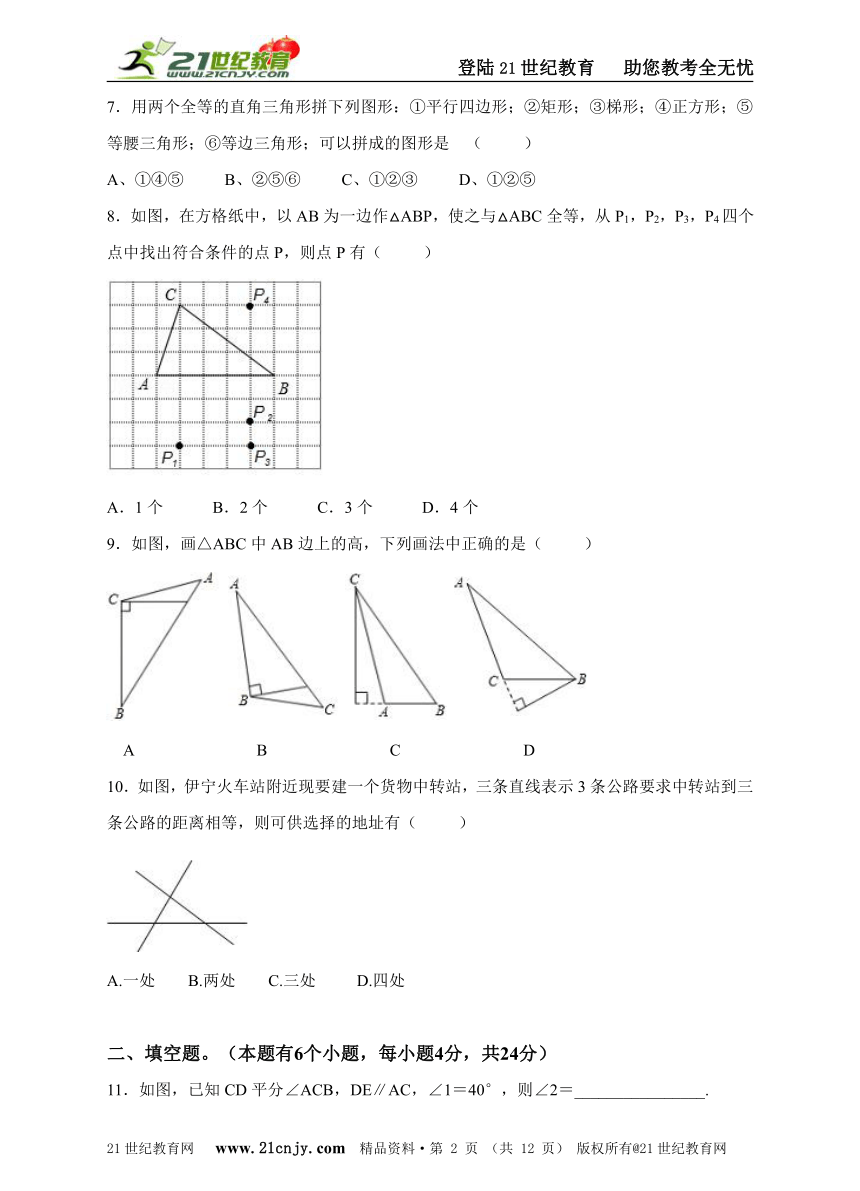
8.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
9.如图,画△ABC中AB边上的高,下列画法中正确的是( )
A B C D 21·世纪*教育网
10.如图,伊宁火车站附近现要建一个货物中转站,三条直线表示3条公路要求中转站到三条公路的距离相等,则可供选择的地址有( )www-2-1-cnjy-com
A.一处 B.两处 C.三处 D.四处
二、填空题。(本题有6个小题,每小题4分,共24分)
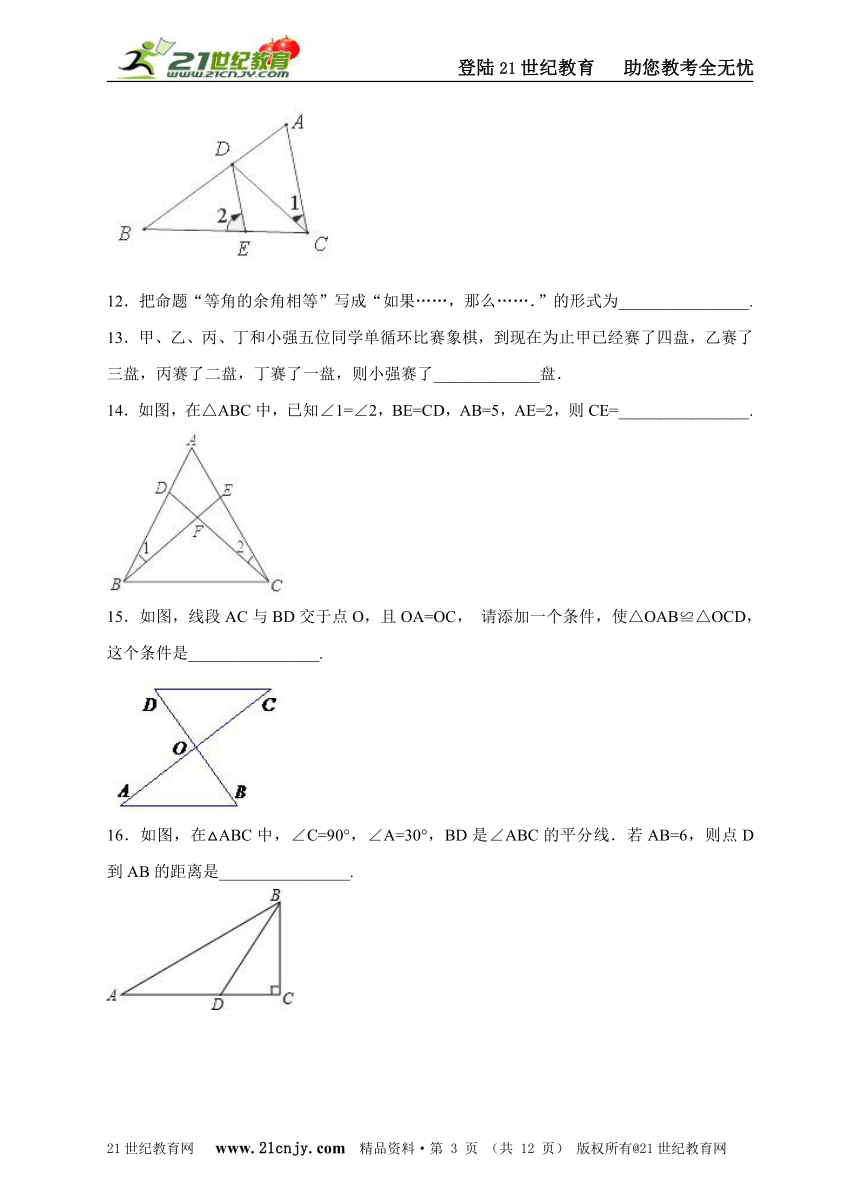
11.如图,已知CD平分∠ACB,DE∥AC,∠1=40°,则∠2=________________.
12.把命题“等角的余角相等”写成“如果……,那么…….”的形式为________________.
13.甲、乙、丙、丁和小强五位同学单循环比赛象棋,到现在为止甲已经赛了四盘,乙赛了三盘,丙赛了二盘,丁赛了一盘,则小强赛了_____________盘.【来源:21cnj*y.co*m】
14.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=________________.
15.如图,线段AC与BD交于点O,且OA=OC, 请添加一个条件,使△OAB≌△OCD,这个条件是________________.21教育名师原创作品
16.如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是________________.
三、解答题。(本题有7个小题,共66分)
17.如图,已知AB=AC,∠ABE=∠ACD,BE与CD相交于O,求证:△ABE≌△ACD。
18.如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M、N分别在AB、AC边上,AM=2MB,AN=2NC,求证:DM=DN。 21*cnjy*com
19.已知:如图,AB∥DE,AB=DE,AF=DC.求证:≌。
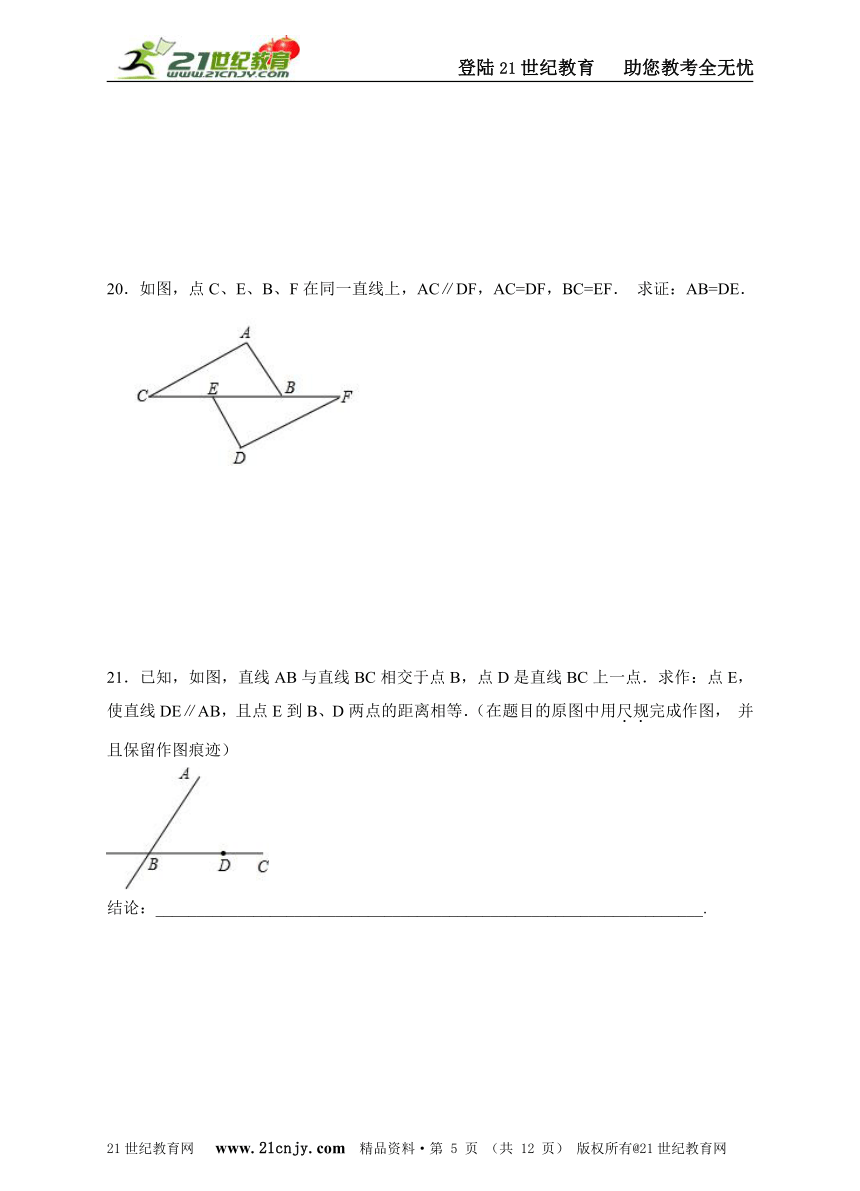
20.如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF. 求证:AB=DE.
21.已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等.(在题目的原图中用尺规完成作图, 并且保留作图痕迹)21*cnjy*com
结论:___________________________________________________________________.
22.如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由.
23.如图,已知△ABC,∠C=Rt∠,AC(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
参考答案与详解
1.B.
【解析】三角形三边长要满足两边之和大于第三边,两边之差小于第三边,这4根木棒选其中的根,能围成三角形的是:①2cm,3cm,4cm.②3cm,4cm,6cm.故选B.
2.D.
【解析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可以求出第三边长的范围.根据题意得:2-1<x<2+1即:1<x<3故选D.21·cn·jy·com
3.C.
【解析】根据三角形的外角等于与它不相邻的内角和,即40o+∠A=120o,∴∠A=80o,故选C.
4.D
【解析】A、两直线平行,则同旁内角互补;B、在同一平面内,垂直于同一条直线的两直线平行;C、邻补角是指一个角.2·1·c·n·j·y
5.C
【解析】他们每天上午、下午各测一次,七次上午晴,五次下午晴,共下八次雨,所以共测了20次,所以这个学生工观察了10天.解:由题意,知:这位学生每天测两次,总共测的次数为7+5+8=20;因此x=20÷2=10(天).故选C.【出处:21教育名师】
6.D.
【解析】根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.故答案选D.【版权所有:21教育】
7.D.
【解析】 根据平行四边形、矩形、菱形、正方形、等腰直角三角形、等腰三角形的判定方法进行逐一分析.
①根据两组对边分别相等的四边形是平行四边形,则可以拼成,如图
②根据有一个角是直角的平行四边形是矩形,则可以拼成,如图
③不能拼成梯形;
④根据有一个角是直角的菱形才是正方形,则不能拼成菱形,当然不能拼成正方形;
⑤根据有两条边相等的三角形即为等腰三角形,所以能拼成,如图:
.
⑥根据三边相等的三角形是等边三角形,所以不能拼成.故选D.
8.C.
【解析】要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,故选C.2-1-c-n-j-y
9.C.
【解析】 过点C作AB边的垂线,正确的是C.
故选:C.
10.D
【解析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.故选D.
11.80°;
【解析】∵CD平分∠ACB;∴∠BCA=2∠1=80°;又∵DE∥AC,∴∠2=∠BCA=80°
12.如果两个角是相等角的余角,那么这两个角相等.
【解析】把命题的题设写在如果的后面,把命题的结论部分写在那么的后面即可.命题“等角的余角相等”写成“如果…,那么….”的形式为:如果两个角是相等角的余角,那么这两个角相等.
13.2
【解析】根据甲赛的盘数,可知甲与乙、丙、丁和小强4人各赛了一盘.然后探究乙、丙、丁和小强4人之间赛的盘数(设小强赛的盘数为x),进而得到小强赛的总盘数.
解:乙、丙、丁和小强除去与甲赛的一盘后,在他们之间赛的盘数分别是:2、1、0、x.即丁只和甲赛了一盘,没与乙、丙、小强比赛,则乙、丙、小强之间赛的盘数分别为2、1、x,假设丙与小强赛了一盘,那么乙赛的两盘都是与小强赛的,这与单循环比赛相矛盾,是不可能的,所以丙与乙赛了一场,乙又与小强赛了一盘,小强与甲也赛了一盘,故小强共赛了2盘.故填2.
14.3.
【解析】△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AD=AE=2,AC=AB=5,∴CE=BD=AB﹣AD=3,故答案为3.
15.∠A=∠C或∠B=∠D或OD=OB或AB∥CD.(添加任意一个即可).
【解析】本题要判定△OAB≌△OCD,已知OA=OC,∠AOB=∠COD,具备了一组边对应相等和一组角对应相等,故添加∠A=∠C,∠B=∠D,OD=OB,AB∥CD后可分别根据ASA、AAS、SAS、AAS判定△OAB≌△OCD.21cnjy.com
16.
【解析】根据三角形的内角和可求出∠ABC=60°,然后根据角平分线的性质求出∠DBC=∠ABC=30°,根据含30°角的直角三角形性质求出BC=AB=3,CD=BC?tan30°=3×=,然后根据角平线上点到角两边距离相等,可求得点D到AB的距离=CD=.
17.证明见解析.
【解析】本题比较简单,三角形全等条件中三个元素都具备,并且一定有一组对应边相等,可用“SAS”.
解:在△ABE与△ACD中.,∴△ABE≌△ACD(SAS).
18.见解析.
【解析】根据AM=2MB,AN=2NC,AB=AC得出AM=AN,根据角平分线得出∠MAD=∠NAD,结合AD=AD得出△AMD和△AND全等,从而得出MD=ND.
解:∵AM=2MB
∴AM=AB 同理AN=AC
又∵AB=AC ∴AM=AN
∵AD平分∠BAC
∴∠MAD=∠NAD 又∵AD=AD
∴△AMD≌△AND
∴DM=DN
19.见解析.
【解析】由AB∥DE可得∠A=∠D, 又因AB=DE,AF=DC,利用“SAS”可得≌.
解:证明:∵AB∥DE∴∠A=∠D∵AB=DE,AF=DC∴≌
20.见解析.
【解析】 证明AB=DE,可以通过全等三角形来求得.三角形ABC和DEF中,已知的条件有:AC=DF,BC=EF,只要再证得两对应边的夹角相等即可得出全等的结论.
解:证明:∵AC∥DF, ∴∠C=∠F.在△ACB和△DFE中
∴△ACB≌△DFE(SAS). ∴AB=DE.
21.作图见解析.
【解析】 首先以D为顶点,DC为边作一个角等于∠ABC,再作出DB的垂直平分线,即可找到点E.
解:如图所示:
点E即为所求.结论:BE=DE.
22.见解析.
【解析】连接AB、EF,交于点M,连接OM,OM即为∠AOB的平分线.根据平行四边形的对角线互相平分可得OM为△AOB的中线,由等腰三角形的三线合一的性质即可得OM为∠AOB的平分线.21教育网
解:如图,连接AB、EF,交于点M,连接OM,OM即为∠AOB的平分线.理由如下:
∵四边形AEBF是平行四边形,
∴AM=BM,EM=FM,
∵OA=OB,
∴OM即为∠AOB的平分线.
23.(1)点D的位置如图所示(D为AB中垂线与BC的交点).(2)16°.
【解析】(1)根据到线段两个端点的距离相等的点在这条线段的垂直平分线上,作出AB的中垂线.(2)要求∠CAD的度数,只需求出∠CAD,而由(1)可知:∠CAD=2∠B
解:(1)点D的位置如图所示(D为AB中垂线与BC的交点).
(2)∵在Rt△ABC中,∠B=37°,∴∠CAB=53°.
又∵AD=BD,∴∠BAD=∠B=37°.
∴∠CAD=53°—37°=16°.
故答案为:(1)点D的位置如图所示(D为AB中垂线与BC的交点);(2)16°.
第1章 三角形的初步知识 (基础检测卷)
题 型
选择题
填空题
解答题
总 分
得 分
一、选择题。(本题有10个小题,每小题3分,共30分)
1.有长为、、、的四根木棒,选其中的根作为三角形的边,可以围成的三角形的个数是( )www.21-cn-jy.com
A.1个 B.2个 C.3个 D.4个
2.一个三角形的三条边长分别为1、2、x,则x的取值范围是( )
A、1≤x≤3 B、1<x≤3 C、1≤x<3 D、1<x<3
3.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A.60° B.70° C.80° D.90
4.下列命题是真命题的是( )
A.同旁内角互补 B.垂直于同一条直线的两直线平行
C.邻补角相等 D.两直线平行,内错角相等
5.某学生在暑假期间观察了x天的天气情况,其结果是:①共有7天上午是晴天;②共有5天下午是晴天;③共下了8次雨;④下午下雨的那天,上午是晴天.则x=( )
A.8 B.9 C.10 D.11
6.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.AAS D.ASA
7.用两个全等的直角三角形拼下列图形:①平行四边形;②矩形;③梯形;④正方形;⑤等腰三角形;⑥等边三角形;可以拼成的图形是 ( )21世纪教育网版权所有
A、①④⑤ B、②⑤⑥ C、①②③ D、①②⑤
8.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
9.如图,画△ABC中AB边上的高,下列画法中正确的是( )
A B C D 21·世纪*教育网
10.如图,伊宁火车站附近现要建一个货物中转站,三条直线表示3条公路要求中转站到三条公路的距离相等,则可供选择的地址有( )www-2-1-cnjy-com
A.一处 B.两处 C.三处 D.四处
二、填空题。(本题有6个小题,每小题4分,共24分)
11.如图,已知CD平分∠ACB,DE∥AC,∠1=40°,则∠2=________________.
12.把命题“等角的余角相等”写成“如果……,那么…….”的形式为________________.
13.甲、乙、丙、丁和小强五位同学单循环比赛象棋,到现在为止甲已经赛了四盘,乙赛了三盘,丙赛了二盘,丁赛了一盘,则小强赛了_____________盘.【来源:21cnj*y.co*m】
14.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=________________.
15.如图,线段AC与BD交于点O,且OA=OC, 请添加一个条件,使△OAB≌△OCD,这个条件是________________.21教育名师原创作品
16.如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是________________.
三、解答题。(本题有7个小题,共66分)
17.如图,已知AB=AC,∠ABE=∠ACD,BE与CD相交于O,求证:△ABE≌△ACD。
18.如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M、N分别在AB、AC边上,AM=2MB,AN=2NC,求证:DM=DN。 21*cnjy*com
19.已知:如图,AB∥DE,AB=DE,AF=DC.求证:≌。
20.如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF. 求证:AB=DE.
21.已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等.(在题目的原图中用尺规完成作图, 并且保留作图痕迹)21*cnjy*com
结论:___________________________________________________________________.
22.如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由.
23.如图,已知△ABC,∠C=Rt∠,AC
(2)连结AD,若∠B=37°,求∠CAD的度数.
参考答案与详解
1.B.
【解析】三角形三边长要满足两边之和大于第三边,两边之差小于第三边,这4根木棒选其中的根,能围成三角形的是:①2cm,3cm,4cm.②3cm,4cm,6cm.故选B.
2.D.
【解析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可以求出第三边长的范围.根据题意得:2-1<x<2+1即:1<x<3故选D.21·cn·jy·com
3.C.
【解析】根据三角形的外角等于与它不相邻的内角和,即40o+∠A=120o,∴∠A=80o,故选C.
4.D
【解析】A、两直线平行,则同旁内角互补;B、在同一平面内,垂直于同一条直线的两直线平行;C、邻补角是指一个角.2·1·c·n·j·y
5.C
【解析】他们每天上午、下午各测一次,七次上午晴,五次下午晴,共下八次雨,所以共测了20次,所以这个学生工观察了10天.解:由题意,知:这位学生每天测两次,总共测的次数为7+5+8=20;因此x=20÷2=10(天).故选C.【出处:21教育名师】
6.D.
【解析】根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.故答案选D.【版权所有:21教育】
7.D.
【解析】 根据平行四边形、矩形、菱形、正方形、等腰直角三角形、等腰三角形的判定方法进行逐一分析.
①根据两组对边分别相等的四边形是平行四边形,则可以拼成,如图
②根据有一个角是直角的平行四边形是矩形,则可以拼成,如图
③不能拼成梯形;
④根据有一个角是直角的菱形才是正方形,则不能拼成菱形,当然不能拼成正方形;
⑤根据有两条边相等的三角形即为等腰三角形,所以能拼成,如图:
.
⑥根据三边相等的三角形是等边三角形,所以不能拼成.故选D.
8.C.
【解析】要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,故选C.2-1-c-n-j-y
9.C.
【解析】 过点C作AB边的垂线,正确的是C.
故选:C.
10.D
【解析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.故选D.
11.80°;
【解析】∵CD平分∠ACB;∴∠BCA=2∠1=80°;又∵DE∥AC,∴∠2=∠BCA=80°
12.如果两个角是相等角的余角,那么这两个角相等.
【解析】把命题的题设写在如果的后面,把命题的结论部分写在那么的后面即可.命题“等角的余角相等”写成“如果…,那么….”的形式为:如果两个角是相等角的余角,那么这两个角相等.
13.2
【解析】根据甲赛的盘数,可知甲与乙、丙、丁和小强4人各赛了一盘.然后探究乙、丙、丁和小强4人之间赛的盘数(设小强赛的盘数为x),进而得到小强赛的总盘数.
解:乙、丙、丁和小强除去与甲赛的一盘后,在他们之间赛的盘数分别是:2、1、0、x.即丁只和甲赛了一盘,没与乙、丙、小强比赛,则乙、丙、小强之间赛的盘数分别为2、1、x,假设丙与小强赛了一盘,那么乙赛的两盘都是与小强赛的,这与单循环比赛相矛盾,是不可能的,所以丙与乙赛了一场,乙又与小强赛了一盘,小强与甲也赛了一盘,故小强共赛了2盘.故填2.
14.3.
【解析】△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AD=AE=2,AC=AB=5,∴CE=BD=AB﹣AD=3,故答案为3.
15.∠A=∠C或∠B=∠D或OD=OB或AB∥CD.(添加任意一个即可).
【解析】本题要判定△OAB≌△OCD,已知OA=OC,∠AOB=∠COD,具备了一组边对应相等和一组角对应相等,故添加∠A=∠C,∠B=∠D,OD=OB,AB∥CD后可分别根据ASA、AAS、SAS、AAS判定△OAB≌△OCD.21cnjy.com
16.
【解析】根据三角形的内角和可求出∠ABC=60°,然后根据角平分线的性质求出∠DBC=∠ABC=30°,根据含30°角的直角三角形性质求出BC=AB=3,CD=BC?tan30°=3×=,然后根据角平线上点到角两边距离相等,可求得点D到AB的距离=CD=.
17.证明见解析.
【解析】本题比较简单,三角形全等条件中三个元素都具备,并且一定有一组对应边相等,可用“SAS”.
解:在△ABE与△ACD中.,∴△ABE≌△ACD(SAS).
18.见解析.
【解析】根据AM=2MB,AN=2NC,AB=AC得出AM=AN,根据角平分线得出∠MAD=∠NAD,结合AD=AD得出△AMD和△AND全等,从而得出MD=ND.
解:∵AM=2MB
∴AM=AB 同理AN=AC
又∵AB=AC ∴AM=AN
∵AD平分∠BAC
∴∠MAD=∠NAD 又∵AD=AD
∴△AMD≌△AND
∴DM=DN
19.见解析.
【解析】由AB∥DE可得∠A=∠D, 又因AB=DE,AF=DC,利用“SAS”可得≌.
解:证明:∵AB∥DE∴∠A=∠D∵AB=DE,AF=DC∴≌
20.见解析.
【解析】 证明AB=DE,可以通过全等三角形来求得.三角形ABC和DEF中,已知的条件有:AC=DF,BC=EF,只要再证得两对应边的夹角相等即可得出全等的结论.
解:证明:∵AC∥DF, ∴∠C=∠F.在△ACB和△DFE中
∴△ACB≌△DFE(SAS). ∴AB=DE.
21.作图见解析.
【解析】 首先以D为顶点,DC为边作一个角等于∠ABC,再作出DB的垂直平分线,即可找到点E.
解:如图所示:
点E即为所求.结论:BE=DE.
22.见解析.
【解析】连接AB、EF,交于点M,连接OM,OM即为∠AOB的平分线.根据平行四边形的对角线互相平分可得OM为△AOB的中线,由等腰三角形的三线合一的性质即可得OM为∠AOB的平分线.21教育网
解:如图,连接AB、EF,交于点M,连接OM,OM即为∠AOB的平分线.理由如下:
∵四边形AEBF是平行四边形,
∴AM=BM,EM=FM,
∵OA=OB,
∴OM即为∠AOB的平分线.
23.(1)点D的位置如图所示(D为AB中垂线与BC的交点).(2)16°.
【解析】(1)根据到线段两个端点的距离相等的点在这条线段的垂直平分线上,作出AB的中垂线.(2)要求∠CAD的度数,只需求出∠CAD,而由(1)可知:∠CAD=2∠B
解:(1)点D的位置如图所示(D为AB中垂线与BC的交点).
(2)∵在Rt△ABC中,∠B=37°,∴∠CAB=53°.
又∵AD=BD,∴∠BAD=∠B=37°.
∴∠CAD=53°—37°=16°.
故答案为:(1)点D的位置如图所示(D为AB中垂线与BC的交点);(2)16°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
