浙教版数学2015-2016学年八年级上册“单元精品卷”第1章 三角形的初步知识(培优提高卷)含精析
文档属性
| 名称 | 浙教版数学2015-2016学年八年级上册“单元精品卷”第1章 三角形的初步知识(培优提高卷)含精析 |  | |
| 格式 | zip | ||
| 文件大小 | 298.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-30 19:42:09 | ||
图片预览



文档简介
2015年浙教版数学八年级上册“单元精品卷”(含精析)
第1章 三角形的初步知识 (培优提高卷)
题 型
选择题
填空题
解答题
总 分
得 分
一、选择题。(本题有10个小题,每小题3分,共30分)
1.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则与和 之间有一种数量关系始终保持不变,你发现的规律是( )www.21-cn-jy.com
A. B.
C. D.
2.如图,将一个直角三角板和一把直尺如图所示放置,如果∠α=43°,则∠β的度数是( )
A.43° B.47° C.30° D.60°
3.下列选项中,可以用来证明命题“若>1,则a>2”是假命题的反例是( )
A.a =2 B.a =1 C.a = 0 D.a =﹣1
4.有A、B、C、D、E共5位同学一起比赛象棋,每两人之间只比赛1盘,比赛过程中间统计比赛的盘数知:A赛了4盘,B赛了3盘,C赛了2盘,D赛了1盘,那么同学E赛了( )盘. 21*cnjy*com
A.1 B.2 C.3 D.4
5.七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )【出处:21教育名师】
A.甲、乙、丙、丁 B.甲、丙、乙、丁 C.甲、丁、乙、丙 D.甲、丙、丁、乙
6.甲、乙、丙、丁四位同学猜测自己的数学成绩,甲说:“如果我得优,那么乙也得优”;乙说:“如果我得优,那么丙也得优”;丙说:“如果我得优,那么丁也得优”,大家都没有说错,但只有三个人得优,请问甲、乙、丙、丁中谁没有得优( )
A.甲 B.乙 C.丙 D.丁
7.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:① AD=BE;② PQ∥AE;③ AP=BQ;④ DE=DP;⑤ ∠AOB=60°.
一定成立的结论有( )
A. ①②③ B. ①②③⑤ C. ②③④ D. ③④⑤
8.如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的个数是( )
①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD;⑤BC=CE
A.0个 B.1个 C.2个 D.3个
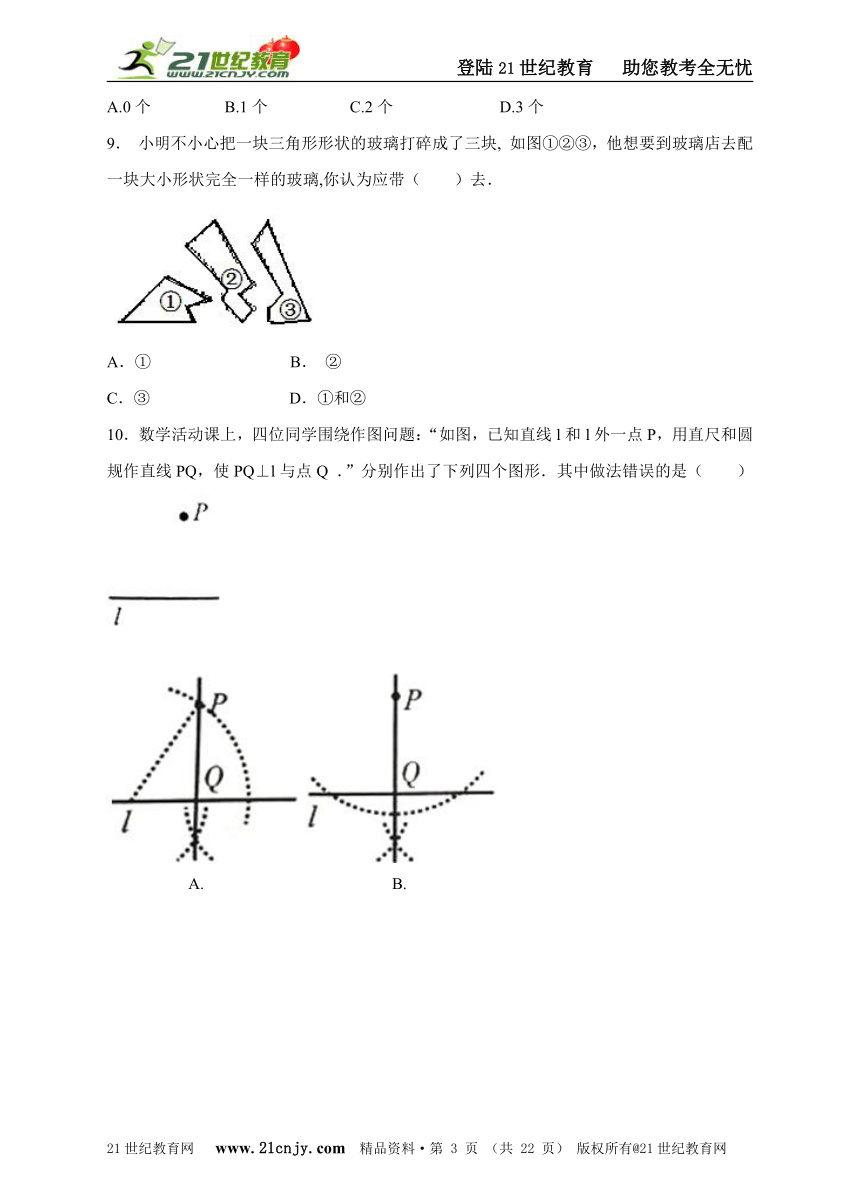
9. 小明不小心把一块三角形形状的玻璃打碎成了三块, 如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )去.
A.① B. ②
C.③ D.①和②
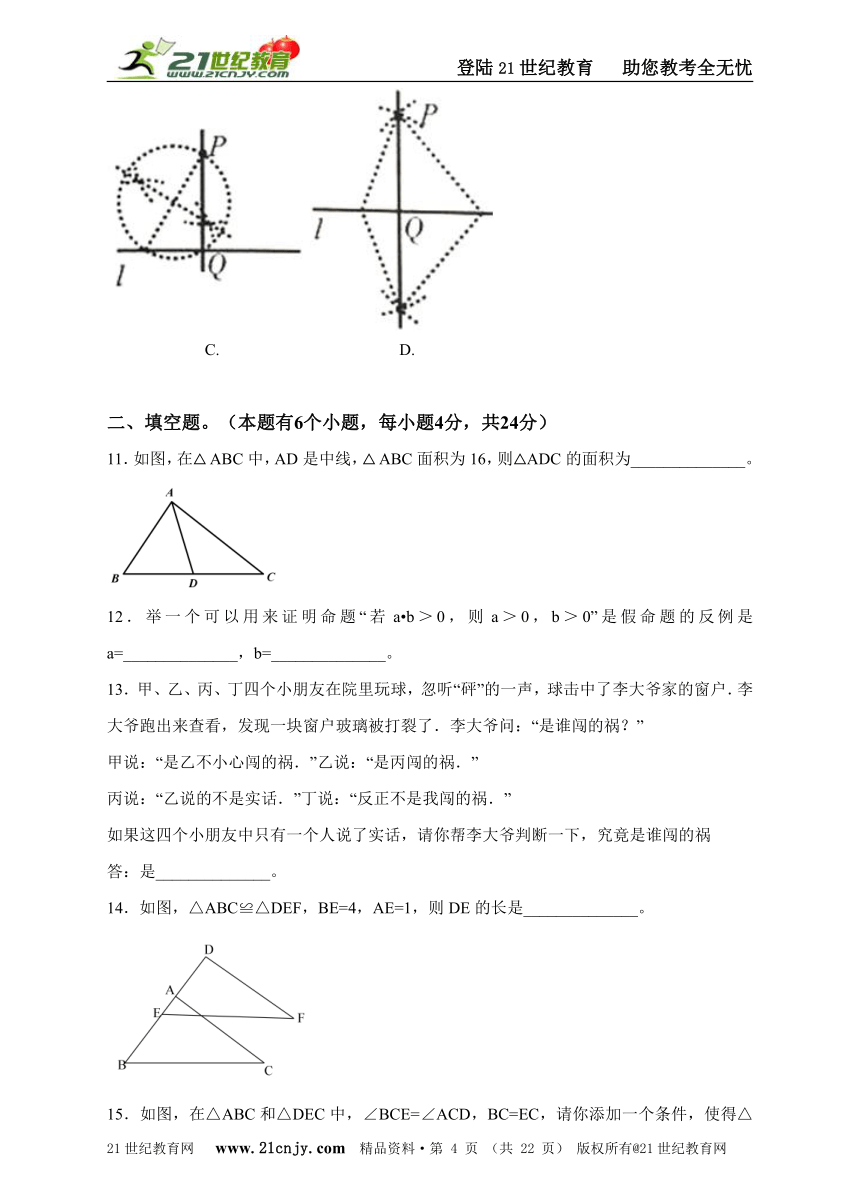
10.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l与点Q .”分别作出了下列四个图形.其中做法错误的是( )
A. B.
C. D.
二、填空题。(本题有6个小题,每小题4分,共24分)
11.如图,在△ ABC中,AD是中线,△ ABC面积为16,则△ADC的面积为______________。
12.举一个可以用来证明命题“若a?b>0,则a>0,b>0”是假命题的反例是a=______________,b=______________。
13.甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来查看,发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?”
甲说:“是乙不小心闯的祸.”乙说:“是丙闯的祸.”
丙说:“乙说的不是实话.”丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸
答:是______________。
14.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是______________。
15.如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等,添加的条件是______________。
16.如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D.则∠ADB的度数为______________。
三、解答题。(本题有7个小题,共66分)
17.(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为____________。
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
18.已知在四边形ABCD中,∠A=x, ∠C=y,(, ).
(1)∠ABC + ∠ADC=______________。(用含x、y的代数式表示) ;
(2)如图1,若x=y=90°,DE平分∠ADC ,BF平分与∠ABC相邻的外角,请写出DE 与 BF 的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x﹤y时,若x+y=140°,∠DFB=30°试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,
∠DFB不存在.
19.如图,在△ABC中,∠ACB=90°,AC=BC=AD.
(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
20.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线
BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
21.三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?21教育网
探究一
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
探究二
(2)如图2,在△ABC纸片中剪去△AED,得到四边形BCDE,∠1=115°,则∠2-∠A=_____;
(3)如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?为什么?
22.如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、 l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连结AP、CE.【版权所有:21教育】
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F,如图,
①当时,求证:AP⊥BD;
②(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求的值.
23.学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
如图1,已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB深入探究:
第一种情况,当BC第二种情况,(1)如图2,当BC=CH时,在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 ,可以知道Rt△ABC≌Rt△DEF.2·1·c·n·j·y
第三种情况,(2)当CH(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF.除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.
(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF.除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.
参考答案与详解
1.A
【解析】根据折叠变换的性质可知∠A=∠,然后根据三角形的外角的性质可知∠+∠2+∠A=∠1,整理后可得2∠A=∠1-∠2.故选A
2.B.
【解析】∠α=43°,与它相邻的补角是137o,五边形内角和是540o,与β相邻的补角是540o-90o-90o-90o-137o=133o,,∴∠β=180o-133o=47o,故选B.
3.D
【解析】根据题意可知所取的a的值符合题意,则不满足结论,即为反例.
当a=2时,=1,是假命题;
当a=1时,=0,是假命题;
当a=0时,=1,是假命题;
当a=-1时,=2>1,但是不满足a>2,是真命题,所以是反例.故选D
4.B
【解析】共有5个人,A赛4盘,则A与B、C、D、E每人赛一盘,则B、C比赛一定不是于D赛的,依此类推即可确定.
解:共有5个人,A赛4盘,则A与B、C、D、E每人赛一盘;
B赛3盘,因为D赛了1盘,则这三盘一定是与A、C、E的比赛;
C赛了两盘,是与A和B赛的.
则E一共赛了2盘,是与A和B赛的.故选B.
5.B
【解析】因为他们每人只猜对一半,可以先假设明明说“甲得第一”是正确的,由此推导:分别分析得出所有的可能即可.
解:因为他们每人只猜对一半,
可以先假设明明说“甲得第一”是正确的,由此推导:
明明:甲得第一→文文:丁得第四→凡凡:丙得第二→乙得第三,成立;
若假设明明说“乙得第二”是正确的,由此进行推导:
明明:乙得第二→文文:丁得第四→凡凡:丙得第二,矛盾.
所以甲、乙、丙、丁的名次顺序为甲、丙、乙、丁.故选B.
6.A
【解析】此题含有一个隐含条件,也就是丁没有说:如果我得优,那么甲也得优…解题可以从这里突破.也就是丁得优,而甲不得优.由此进行推理即可得到结论.
解:∵这个题还有一个隐含条件,也就是丁没有说:如果我得优,那么甲也得优…,也就是丁得优,而甲不得优.
如果甲不得优,乙可得可不得优;
如果乙不得优,而丁可以得优也可以不得优;
如果丁一定要得优,因为题中说有3人得优,所以按反推法,有丙也得优;
如果问题是1人得优,那肯定是丁,如果2人得优,那肯定是丁、丙.
如果3人得优,那肯定是丁、丙、乙.故选A.
7.B
【解析】①∵正△ABC和正△CDE,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ADC≌△BEC(SAS),∴AD=BE,∠ADC=∠BEC,(故①正确);21·世纪*教育网
②又∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,∴∠QPC=∠BCA,∴PQ∥AE,(故②正确);
③∵△CDP≌△CEQ,∴DP=QE,∵△ADC≌△BEC,∴AD=BE,∴AD﹣DP=BE﹣QE,∴AP=BQ,(故③正确);2-1-c-n-j-y
④∵DE>QE,且DP=QE,∴DE>DP,(故④错误);
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,(故⑤正确).∴正确的有:①②③⑤.21*cnjy*com
故答案为:①②③⑤.
8.B.
【解析】∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵AE、BE分别是∠BAD与∠ABC的平分线,
∴∠BAE=∠BAD,∠ABE=∠ABC,
∴∠BAE+∠ABE=(∠BAD+∠ABC)=90°,
∴∠AEB=180°-(∠BAE+∠ABE)=180°-90°=90°,
故③小题正确;
延长AE交BC延长线于F,
∵∠AEB=90°,
∴BE⊥AF,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE与△FBE中,
,
∴△ABE≌△FBE(ASA),
∴AB=BF,AE=FE,
∵AD∥BC,
∴∠EAD=∠F,
在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴AD=CF,
∴AB=BC+CF=BC+AD,故①小题正确;
∵△ADE≌△FCE,
∴CE=DE,即点E为CD的中点,故②小题正确;
∵△ADE≌△FCE,
∴S△ADE=S△FCE,
∴S四边形ABCD=S△ABF,
∵S△ABE=S△ABE,
∴S△ABE=S四边形ABCD,故④小题正确;
若AD=BC,则CE是Rt△BEF斜边上的中线,则BC=CE,
∵BD与BC不一定相等,
∴BC与CE不一定相等,故⑤小题错误.
综上所述,不正确的有⑤共1个.故选B.
9.C
【解析】全等三角形的条件是.∴选C.其它残品中不够全等的条件.
10.A
【解析】A、根据作法无法判定PQ⊥l;
B、以P为圆心大于P到直线l的距离为半径画弧,交直线l,于两点,再以两点为圆心,大于它们的长为半径画弧,得出其交点,进而作出判断;21世纪教育网版权所有
C、根据直径所对的圆周角等于90°作出判断;
D、根据全等三角形的判定和性质即可作出判断.
所以选项B、C、D都能够得到PQ⊥l于点Q;选项A不能够得到PQ⊥l于点Q.故选:A.
11.8
【解析】根据AD是△ABC的中线可知BD=DC,然后根据等底同高可知△ABD的面积等于△ADC的面积,因此△ADC的面积是△ABC的面积的一半,即△ADC的面积为8.
12.﹣1,﹣2
【解析】根据要证明一个结论不成立,可以通过举反例的方法来证明一个命题是假命题.
解:用来证明命题“若a?b>0,则a>0,b>0”是假命题的反例是a=﹣1,b=﹣2,
故答案为﹣1,﹣2.
13.丁是真正闯祸的人
【解析】若甲说的是真话,则乙是假话,丙说的是真话,和已知不符合.故甲说的是假话,不是乙闯的祸;若乙说的是真话,则丁说的也是真话,和已知不符合.故乙说的是假话,不是丙闯的祸.显然丙说的是真话,丁说的是假话,则是丁闯的祸.21cnjy.com
解:本题可分三种情况:
①如果甲是真命题,则乙是假命题,丙是真命题,丁是真命题;显然与已知不符;
②如果甲是假命题,乙是真命题,则丙是假命题,丁是真命题;显然与已知不符;
③如果甲是假命题,乙是假命题,则丙是真命题,丁是假命题;在这种情况下,只有丙说了实话,而其他人都说了假话,因此这种情况符合题意.www-2-1-cnjy-com
在③的条件下,丁说了假话,因此丁才是真正闯祸的人.
14.5.
【解析】全等三角形的对应边相等,DE=AB,AB=AE+BE=4+1=5,所以DE=5.
15.CD=CA或∠E=∠B,∠D=∠A
【解析】添加条件CD=CA,利用SAS判定△ABC≌△DEC.添加其它条件∠E=∠B或∠D=∠A,
利用AAS或ASA判定△ABC≌△DEC也可.
16.100°
【解析】根据已知条件中的作图步骤知,AG是∠CAB的平分线,根据角平分线的性质解答即可.
解:根据已知条件中的作图步骤知,AG是∠CAB的平分线,
∵∠ACB=80°,∠ABC=60°,
∴∠CAB=40°,
∴∠BAD=20°;
在△ADB中,∠B=60°,∠CAD=20°,
∴∠ADB=100°
17.(1)EF=BE+DF;(2)成立;(3)583m.
【解析】根据全等三角形对应边相等解答;延长FD到G,使DG=BE,连接AG,根据同角的补角相等求出∠B=∠ADG,然后利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AE=AG,∠BAE=∠DAG,再求出∠EAF=∠GAF,然后利用“边角边”证明△AEF和△GAF全等,根据全等三角形对应边相等可得EF=GF,然后求解即可;连接EF,延长AE、BF相交于点C,然后求出∠EAF=∠AOB,判断出符合探索延伸的条件,再根据探索延伸的结论解答即可。
解:(1)EF=BE+DF;
证明:如图1,延长FD到G,使DG=BE,连接AG, 在△ABE和△ADG中, ,
∴△ABE≌△ADG(SAS), ∴AE=AG,∠BAE=∠DAG, ∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF, ∴∠EAF=∠GAF,
在△AEF和△GAF中, , ∴△AEF≌△GAF(SAS), ∴EF=FG,
∵FG=DG+DF=BE+DF, ∴EF=BE+DF;
(2)EF=BE+DF仍然成立.
证明:如图2,延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠B=∠ADG,在△ABE和△ADG中, , ∴△ABE≌△ADG(SAS), ∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD, ∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF, ∴∠EAF=∠GAF,
在△AEF和△GAF中, , ∴△AEF≌△GAF(SAS), ∴EF=FG, ∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)如图3,连接EF,延长AE、BF相交于点C, ∵∠AOB=20°+90°+(90°﹣60°)=140°,∠EOF=70°,
∴∠EOF=∠AOB, 又∵OA=OB, ∠OAC+∠OBC=(90°﹣20°)+(60°+50°)=180°,
∴符合探索延伸中的条件, ∴结论EF=AE+BF成立, 即EF=583米.
18.(1)360°-x-y(2)(3)①x=40°,y=100°②x=y
【解析】(1)根据四边形的内角和为360°可求解;
(2),延长DE交BF与G,然后根据角平分线的性质和(1)的结论证得∠EGB=90°;
(3)由(1)的结论和角平分线的性质可得∠CDF+∠CBF= (x+y) ,
因此可得∠FBD+∠FDB=180°-y+(x+y)=180°-y+x ,∠DFB=y-x= 30°,然后由x+y=40°,联立方程组可求得x、y;根据题意可知当x=y时,四边形中的点C与F点重合,故不存在.
连接DB,可得∠CBD+∠CDB=180°- y,
解:(1)360°-x-y
(2)延长DE交BF于G
因为DE平分∠ADC,BF平分∠MBC
所以∠CDE=∠ADC,∠CBF=∠CBM
又因为∠CBM=-∠ABC=-=∠ADC
所以∠CDE=∠CBF
又因为∠BED=∠CDE+∠C=∠CBF+∠BGE
所以∠BGE=∠C=
所以(即)
(3)①由(1)得:∠CDN+∠CBM= x+y
因为BF、DF分别平分∠CBM、∠CDN
所以∠CDF+∠CBF= (x+y)
连接DB, 则∠CBD+∠CDB=180°- y
得∠FBD+∠FDB=180°- y+ (x+y)=180°- y+x
所以∠DFB= y-x =30°,解方程组,得x=40°,y=100°
②x=y
19.(1)作图见试题解析;(2)作图见试题解析;(3)△ACE≌△ADE,△ACE≌△CFB.
【解析】
(1)利用角平分线的作法得出∠A的平分线;
(2)利用钝角三角形高线的作法得出BF;
(3)利用等腰三角形的性质及全等三角形的判定得出答案.
解:(1)如图所示:AE即为所求;
(2)如图所示:BF即为所求;
(3)如图所示:△ACE≌△ADE,△ACE≌△CFB,
∵AC=AD,AE平分∠CAD,∴AE⊥CD,EC=DE,在△ACE和△ADE中,∵AE=AE,∠AEC=∠AED,EC=ED,∴△ACE≌△ADE(SAS).【来源:21·世纪·教育·网】
20.(1)详见解析;(2)BE+CF>EF,理由见解析.
【解析】(1)利用ASA(或AAS)证明△GBD≌△FCD,再根据全等三角形的性质即可得BG=CF.(2)再证△GDE≌△FDE,根据全等三角形的性质即可得EG=EF,在△BEG中,根据三角形的三边关系可得BE+BG>GE,即可得BE+CF>EF.【来源:21cnj*y.co*m】
解:(1)∵AC∥BG,
∴∠GBD=∠C,
在△GBD与△FCD中,∠GBD=∠C,BD=CD,∠BDG=∠CDF,
∴△GBD≌△FCD,∴BG=CF.
(2)BE+CF>EF,理由如下,
又∵△GBD≌△FCD(已证) ,
∴GD=FD,
在△GDE与△FDE中,GD=FD,∠GDE=∠FDE=90°,DE=DE,
∴△GDE≌△FDE(SAS) ,
∴EG=EF,
∵BE+BG>GE,
∴BE+CF>EF.
21.(1)∠DBC+∠ECB=180°+∠A;(2)65°;(3),理由参见解析.
【解析】(1)利用三角形外角性质与三角形内角和180度导出.(2)∠2-∠A等于∠1的邻补角,先把这个邻补角求出来,问题就解决了.(3)利用三角形外角性质与三角形内角和是180度建立∠P与∠A的关系.
解:(1)∵三角形的一个外角等于与它不相邻的两个内角的和.即:∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=180°+∠A;(2)∵∠1=115°,∴∠ADE=180-115=65o,∵∠A+∠ADE=∠2,∴∠2-∠A=∠ADE=65o.(3)由题意得∠P=180-∠DBC-∠ECB=180-(∠DBC+ECB)=180-(∠A+∠ACB+∠A+∠ABC)=180-(180+∠A)=180-90-∠A=90-∠A.
22.(1)详见解析;(2)①详见解析;②.
【解析】(1)利用“SAS”可判定△ABP≌△CBE;(2)①因为△ABP≌△CBE,所以∠PAB=∠ECB,则∠PAB+∠AEH=∠ECB+∠AEH=90°,所以AP⊥CE.因为=2,即P是BC的中点,利用对角线互相平分的四边形是平行四边形易得四边形BECD是平行四边形,则BD∥CE,所以AP⊥BD.②设△PBE的面积为S,分别用S表示出△PAD和△PCE的面积,代入求出即可.
解:(1)易知,所以△ABP≌△CBE;
(2)延长AP交CE于点H,
因为△ABP≌△CBE,所以∠PAB=∠ECB,
则∠PAB+∠AEH=∠ECB+∠AEH=90°,所以AP⊥CE.
因为=2,即P是BC的中点,
则BD∥CE,所以AP⊥BD.
②因为,即BC=n·BP,所以CP=(n-1)·BP,因为CD∥BE,易得△CPD∽△BPE,所以,设△PBE的面积为S,△PCE的面积为S2满足.S2=(n-1)·S,又S△PAB=S△BCE= n·S,所以S△PAE=( n+1)·S,又因为,所以S1=(n-1)·S△PAE,即S1=(n+1)(n-1)·S,21·cn·jy·com
所以.
23.(1)HL或AAS;(2)图形详见解析;(3)当BC≥CA时,也能使ABC≌△DEF.证明详见解析.
【解析】(1)当BC=CH时,根据三角形全等的判定方法作答,可以是HL或AAS;
(2)当CH(3)当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,根据AAS易证两三角形全等,当BC>CA时,过点F作FG⊥DE于点G,通过证明△CAH≌△FDG(AAS),得到CH=FG,通过证明Rt△CBH≌Rt△FEG(HL),得到∠CBA=∠FED,最后证得△ABC≌△DEF(AAS).
解:(1)HL或AAS;
(2)如图:
(3)当BC≥CA时,也能使ABC≌△DEF.
证明:当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,根据AAS易证两三角形全等,当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,过点F作FG⊥DE于点G,
在△CAH和△FDG中,
,
∴△CAH≌△FDG(AAS),
∴CH=FG,
在Rt△CBH和Rt△FEG中,
,
∴Rt△CBH≌Rt△FEG(HL),
∴∠CBA=∠FED,
在△ABC和△EFD中,
,
∴△ABC≌△DEF(AAS).
第1章 三角形的初步知识 (培优提高卷)
题 型
选择题
填空题
解答题
总 分
得 分
一、选择题。(本题有10个小题,每小题3分,共30分)
1.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则与和 之间有一种数量关系始终保持不变,你发现的规律是( )www.21-cn-jy.com
A. B.
C. D.
2.如图,将一个直角三角板和一把直尺如图所示放置,如果∠α=43°,则∠β的度数是( )
A.43° B.47° C.30° D.60°
3.下列选项中,可以用来证明命题“若>1,则a>2”是假命题的反例是( )
A.a =2 B.a =1 C.a = 0 D.a =﹣1
4.有A、B、C、D、E共5位同学一起比赛象棋,每两人之间只比赛1盘,比赛过程中间统计比赛的盘数知:A赛了4盘,B赛了3盘,C赛了2盘,D赛了1盘,那么同学E赛了( )盘. 21*cnjy*com
A.1 B.2 C.3 D.4
5.七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )【出处:21教育名师】
A.甲、乙、丙、丁 B.甲、丙、乙、丁 C.甲、丁、乙、丙 D.甲、丙、丁、乙
6.甲、乙、丙、丁四位同学猜测自己的数学成绩,甲说:“如果我得优,那么乙也得优”;乙说:“如果我得优,那么丙也得优”;丙说:“如果我得优,那么丁也得优”,大家都没有说错,但只有三个人得优,请问甲、乙、丙、丁中谁没有得优( )
A.甲 B.乙 C.丙 D.丁
7.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:① AD=BE;② PQ∥AE;③ AP=BQ;④ DE=DP;⑤ ∠AOB=60°.
一定成立的结论有( )
A. ①②③ B. ①②③⑤ C. ②③④ D. ③④⑤
8.如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的个数是( )
①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD;⑤BC=CE
A.0个 B.1个 C.2个 D.3个
9. 小明不小心把一块三角形形状的玻璃打碎成了三块, 如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )去.
A.① B. ②
C.③ D.①和②
10.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l与点Q .”分别作出了下列四个图形.其中做法错误的是( )
A. B.
C. D.
二、填空题。(本题有6个小题,每小题4分,共24分)
11.如图,在△ ABC中,AD是中线,△ ABC面积为16,则△ADC的面积为______________。
12.举一个可以用来证明命题“若a?b>0,则a>0,b>0”是假命题的反例是a=______________,b=______________。
13.甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来查看,发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?”
甲说:“是乙不小心闯的祸.”乙说:“是丙闯的祸.”
丙说:“乙说的不是实话.”丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸
答:是______________。
14.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是______________。
15.如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等,添加的条件是______________。
16.如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D.则∠ADB的度数为______________。
三、解答题。(本题有7个小题,共66分)
17.(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为____________。
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
18.已知在四边形ABCD中,∠A=x, ∠C=y,(, ).
(1)∠ABC + ∠ADC=______________。(用含x、y的代数式表示) ;
(2)如图1,若x=y=90°,DE平分∠ADC ,BF平分与∠ABC相邻的外角,请写出DE 与 BF 的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x﹤y时,若x+y=140°,∠DFB=30°试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,
∠DFB不存在.
19.如图,在△ABC中,∠ACB=90°,AC=BC=AD.
(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
20.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线
BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
21.三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?21教育网
探究一
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
探究二
(2)如图2,在△ABC纸片中剪去△AED,得到四边形BCDE,∠1=115°,则∠2-∠A=_____;
(3)如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?为什么?
22.如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、 l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连结AP、CE.【版权所有:21教育】
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F,如图,
①当时,求证:AP⊥BD;
②(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求的值.
23.学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
如图1,已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB
第一种情况,当BC
第三种情况,(2)当CH
(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF.除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.
参考答案与详解
1.A
【解析】根据折叠变换的性质可知∠A=∠,然后根据三角形的外角的性质可知∠+∠2+∠A=∠1,整理后可得2∠A=∠1-∠2.故选A
2.B.
【解析】∠α=43°,与它相邻的补角是137o,五边形内角和是540o,与β相邻的补角是540o-90o-90o-90o-137o=133o,,∴∠β=180o-133o=47o,故选B.
3.D
【解析】根据题意可知所取的a的值符合题意,则不满足结论,即为反例.
当a=2时,=1,是假命题;
当a=1时,=0,是假命题;
当a=0时,=1,是假命题;
当a=-1时,=2>1,但是不满足a>2,是真命题,所以是反例.故选D
4.B
【解析】共有5个人,A赛4盘,则A与B、C、D、E每人赛一盘,则B、C比赛一定不是于D赛的,依此类推即可确定.
解:共有5个人,A赛4盘,则A与B、C、D、E每人赛一盘;
B赛3盘,因为D赛了1盘,则这三盘一定是与A、C、E的比赛;
C赛了两盘,是与A和B赛的.
则E一共赛了2盘,是与A和B赛的.故选B.
5.B
【解析】因为他们每人只猜对一半,可以先假设明明说“甲得第一”是正确的,由此推导:分别分析得出所有的可能即可.
解:因为他们每人只猜对一半,
可以先假设明明说“甲得第一”是正确的,由此推导:
明明:甲得第一→文文:丁得第四→凡凡:丙得第二→乙得第三,成立;
若假设明明说“乙得第二”是正确的,由此进行推导:
明明:乙得第二→文文:丁得第四→凡凡:丙得第二,矛盾.
所以甲、乙、丙、丁的名次顺序为甲、丙、乙、丁.故选B.
6.A
【解析】此题含有一个隐含条件,也就是丁没有说:如果我得优,那么甲也得优…解题可以从这里突破.也就是丁得优,而甲不得优.由此进行推理即可得到结论.
解:∵这个题还有一个隐含条件,也就是丁没有说:如果我得优,那么甲也得优…,也就是丁得优,而甲不得优.
如果甲不得优,乙可得可不得优;
如果乙不得优,而丁可以得优也可以不得优;
如果丁一定要得优,因为题中说有3人得优,所以按反推法,有丙也得优;
如果问题是1人得优,那肯定是丁,如果2人得优,那肯定是丁、丙.
如果3人得优,那肯定是丁、丙、乙.故选A.
7.B
【解析】①∵正△ABC和正△CDE,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ADC≌△BEC(SAS),∴AD=BE,∠ADC=∠BEC,(故①正确);21·世纪*教育网
②又∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,∴∠QPC=∠BCA,∴PQ∥AE,(故②正确);
③∵△CDP≌△CEQ,∴DP=QE,∵△ADC≌△BEC,∴AD=BE,∴AD﹣DP=BE﹣QE,∴AP=BQ,(故③正确);2-1-c-n-j-y
④∵DE>QE,且DP=QE,∴DE>DP,(故④错误);
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,(故⑤正确).∴正确的有:①②③⑤.21*cnjy*com
故答案为:①②③⑤.
8.B.
【解析】∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵AE、BE分别是∠BAD与∠ABC的平分线,
∴∠BAE=∠BAD,∠ABE=∠ABC,
∴∠BAE+∠ABE=(∠BAD+∠ABC)=90°,
∴∠AEB=180°-(∠BAE+∠ABE)=180°-90°=90°,
故③小题正确;
延长AE交BC延长线于F,
∵∠AEB=90°,
∴BE⊥AF,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE与△FBE中,
,
∴△ABE≌△FBE(ASA),
∴AB=BF,AE=FE,
∵AD∥BC,
∴∠EAD=∠F,
在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴AD=CF,
∴AB=BC+CF=BC+AD,故①小题正确;
∵△ADE≌△FCE,
∴CE=DE,即点E为CD的中点,故②小题正确;
∵△ADE≌△FCE,
∴S△ADE=S△FCE,
∴S四边形ABCD=S△ABF,
∵S△ABE=S△ABE,
∴S△ABE=S四边形ABCD,故④小题正确;
若AD=BC,则CE是Rt△BEF斜边上的中线,则BC=CE,
∵BD与BC不一定相等,
∴BC与CE不一定相等,故⑤小题错误.
综上所述,不正确的有⑤共1个.故选B.
9.C
【解析】全等三角形的条件是.∴选C.其它残品中不够全等的条件.
10.A
【解析】A、根据作法无法判定PQ⊥l;
B、以P为圆心大于P到直线l的距离为半径画弧,交直线l,于两点,再以两点为圆心,大于它们的长为半径画弧,得出其交点,进而作出判断;21世纪教育网版权所有
C、根据直径所对的圆周角等于90°作出判断;
D、根据全等三角形的判定和性质即可作出判断.
所以选项B、C、D都能够得到PQ⊥l于点Q;选项A不能够得到PQ⊥l于点Q.故选:A.
11.8
【解析】根据AD是△ABC的中线可知BD=DC,然后根据等底同高可知△ABD的面积等于△ADC的面积,因此△ADC的面积是△ABC的面积的一半,即△ADC的面积为8.
12.﹣1,﹣2
【解析】根据要证明一个结论不成立,可以通过举反例的方法来证明一个命题是假命题.
解:用来证明命题“若a?b>0,则a>0,b>0”是假命题的反例是a=﹣1,b=﹣2,
故答案为﹣1,﹣2.
13.丁是真正闯祸的人
【解析】若甲说的是真话,则乙是假话,丙说的是真话,和已知不符合.故甲说的是假话,不是乙闯的祸;若乙说的是真话,则丁说的也是真话,和已知不符合.故乙说的是假话,不是丙闯的祸.显然丙说的是真话,丁说的是假话,则是丁闯的祸.21cnjy.com
解:本题可分三种情况:
①如果甲是真命题,则乙是假命题,丙是真命题,丁是真命题;显然与已知不符;
②如果甲是假命题,乙是真命题,则丙是假命题,丁是真命题;显然与已知不符;
③如果甲是假命题,乙是假命题,则丙是真命题,丁是假命题;在这种情况下,只有丙说了实话,而其他人都说了假话,因此这种情况符合题意.www-2-1-cnjy-com
在③的条件下,丁说了假话,因此丁才是真正闯祸的人.
14.5.
【解析】全等三角形的对应边相等,DE=AB,AB=AE+BE=4+1=5,所以DE=5.
15.CD=CA或∠E=∠B,∠D=∠A
【解析】添加条件CD=CA,利用SAS判定△ABC≌△DEC.添加其它条件∠E=∠B或∠D=∠A,
利用AAS或ASA判定△ABC≌△DEC也可.
16.100°
【解析】根据已知条件中的作图步骤知,AG是∠CAB的平分线,根据角平分线的性质解答即可.
解:根据已知条件中的作图步骤知,AG是∠CAB的平分线,
∵∠ACB=80°,∠ABC=60°,
∴∠CAB=40°,
∴∠BAD=20°;
在△ADB中,∠B=60°,∠CAD=20°,
∴∠ADB=100°
17.(1)EF=BE+DF;(2)成立;(3)583m.
【解析】根据全等三角形对应边相等解答;延长FD到G,使DG=BE,连接AG,根据同角的补角相等求出∠B=∠ADG,然后利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AE=AG,∠BAE=∠DAG,再求出∠EAF=∠GAF,然后利用“边角边”证明△AEF和△GAF全等,根据全等三角形对应边相等可得EF=GF,然后求解即可;连接EF,延长AE、BF相交于点C,然后求出∠EAF=∠AOB,判断出符合探索延伸的条件,再根据探索延伸的结论解答即可。
解:(1)EF=BE+DF;
证明:如图1,延长FD到G,使DG=BE,连接AG, 在△ABE和△ADG中, ,
∴△ABE≌△ADG(SAS), ∴AE=AG,∠BAE=∠DAG, ∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF, ∴∠EAF=∠GAF,
在△AEF和△GAF中, , ∴△AEF≌△GAF(SAS), ∴EF=FG,
∵FG=DG+DF=BE+DF, ∴EF=BE+DF;
(2)EF=BE+DF仍然成立.
证明:如图2,延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠B=∠ADG,在△ABE和△ADG中, , ∴△ABE≌△ADG(SAS), ∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD, ∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF, ∴∠EAF=∠GAF,
在△AEF和△GAF中, , ∴△AEF≌△GAF(SAS), ∴EF=FG, ∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)如图3,连接EF,延长AE、BF相交于点C, ∵∠AOB=20°+90°+(90°﹣60°)=140°,∠EOF=70°,
∴∠EOF=∠AOB, 又∵OA=OB, ∠OAC+∠OBC=(90°﹣20°)+(60°+50°)=180°,
∴符合探索延伸中的条件, ∴结论EF=AE+BF成立, 即EF=583米.
18.(1)360°-x-y(2)(3)①x=40°,y=100°②x=y
【解析】(1)根据四边形的内角和为360°可求解;
(2),延长DE交BF与G,然后根据角平分线的性质和(1)的结论证得∠EGB=90°;
(3)由(1)的结论和角平分线的性质可得∠CDF+∠CBF= (x+y) ,
因此可得∠FBD+∠FDB=180°-y+(x+y)=180°-y+x ,∠DFB=y-x= 30°,然后由x+y=40°,联立方程组可求得x、y;根据题意可知当x=y时,四边形中的点C与F点重合,故不存在.
连接DB,可得∠CBD+∠CDB=180°- y,
解:(1)360°-x-y
(2)延长DE交BF于G
因为DE平分∠ADC,BF平分∠MBC
所以∠CDE=∠ADC,∠CBF=∠CBM
又因为∠CBM=-∠ABC=-=∠ADC
所以∠CDE=∠CBF
又因为∠BED=∠CDE+∠C=∠CBF+∠BGE
所以∠BGE=∠C=
所以(即)
(3)①由(1)得:∠CDN+∠CBM= x+y
因为BF、DF分别平分∠CBM、∠CDN
所以∠CDF+∠CBF= (x+y)
连接DB, 则∠CBD+∠CDB=180°- y
得∠FBD+∠FDB=180°- y+ (x+y)=180°- y+x
所以∠DFB= y-x =30°,解方程组,得x=40°,y=100°
②x=y
19.(1)作图见试题解析;(2)作图见试题解析;(3)△ACE≌△ADE,△ACE≌△CFB.
【解析】
(1)利用角平分线的作法得出∠A的平分线;
(2)利用钝角三角形高线的作法得出BF;
(3)利用等腰三角形的性质及全等三角形的判定得出答案.
解:(1)如图所示:AE即为所求;
(2)如图所示:BF即为所求;
(3)如图所示:△ACE≌△ADE,△ACE≌△CFB,
∵AC=AD,AE平分∠CAD,∴AE⊥CD,EC=DE,在△ACE和△ADE中,∵AE=AE,∠AEC=∠AED,EC=ED,∴△ACE≌△ADE(SAS).【来源:21·世纪·教育·网】
20.(1)详见解析;(2)BE+CF>EF,理由见解析.
【解析】(1)利用ASA(或AAS)证明△GBD≌△FCD,再根据全等三角形的性质即可得BG=CF.(2)再证△GDE≌△FDE,根据全等三角形的性质即可得EG=EF,在△BEG中,根据三角形的三边关系可得BE+BG>GE,即可得BE+CF>EF.【来源:21cnj*y.co*m】
解:(1)∵AC∥BG,
∴∠GBD=∠C,
在△GBD与△FCD中,∠GBD=∠C,BD=CD,∠BDG=∠CDF,
∴△GBD≌△FCD,∴BG=CF.
(2)BE+CF>EF,理由如下,
又∵△GBD≌△FCD(已证) ,
∴GD=FD,
在△GDE与△FDE中,GD=FD,∠GDE=∠FDE=90°,DE=DE,
∴△GDE≌△FDE(SAS) ,
∴EG=EF,
∵BE+BG>GE,
∴BE+CF>EF.
21.(1)∠DBC+∠ECB=180°+∠A;(2)65°;(3),理由参见解析.
【解析】(1)利用三角形外角性质与三角形内角和180度导出.(2)∠2-∠A等于∠1的邻补角,先把这个邻补角求出来,问题就解决了.(3)利用三角形外角性质与三角形内角和是180度建立∠P与∠A的关系.
解:(1)∵三角形的一个外角等于与它不相邻的两个内角的和.即:∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=180°+∠A;(2)∵∠1=115°,∴∠ADE=180-115=65o,∵∠A+∠ADE=∠2,∴∠2-∠A=∠ADE=65o.(3)由题意得∠P=180-∠DBC-∠ECB=180-(∠DBC+ECB)=180-(∠A+∠ACB+∠A+∠ABC)=180-(180+∠A)=180-90-∠A=90-∠A.
22.(1)详见解析;(2)①详见解析;②.
【解析】(1)利用“SAS”可判定△ABP≌△CBE;(2)①因为△ABP≌△CBE,所以∠PAB=∠ECB,则∠PAB+∠AEH=∠ECB+∠AEH=90°,所以AP⊥CE.因为=2,即P是BC的中点,利用对角线互相平分的四边形是平行四边形易得四边形BECD是平行四边形,则BD∥CE,所以AP⊥BD.②设△PBE的面积为S,分别用S表示出△PAD和△PCE的面积,代入求出即可.
解:(1)易知,所以△ABP≌△CBE;
(2)延长AP交CE于点H,
因为△ABP≌△CBE,所以∠PAB=∠ECB,
则∠PAB+∠AEH=∠ECB+∠AEH=90°,所以AP⊥CE.
因为=2,即P是BC的中点,
则BD∥CE,所以AP⊥BD.
②因为,即BC=n·BP,所以CP=(n-1)·BP,因为CD∥BE,易得△CPD∽△BPE,所以,设△PBE的面积为S,△PCE的面积为S2满足.S2=(n-1)·S,又S△PAB=S△BCE= n·S,所以S△PAE=( n+1)·S,又因为,所以S1=(n-1)·S△PAE,即S1=(n+1)(n-1)·S,21·cn·jy·com
所以.
23.(1)HL或AAS;(2)图形详见解析;(3)当BC≥CA时,也能使ABC≌△DEF.证明详见解析.
【解析】(1)当BC=CH时,根据三角形全等的判定方法作答,可以是HL或AAS;
(2)当CH
解:(1)HL或AAS;
(2)如图:
(3)当BC≥CA时,也能使ABC≌△DEF.
证明:当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,根据AAS易证两三角形全等,当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,过点F作FG⊥DE于点G,
在△CAH和△FDG中,
,
∴△CAH≌△FDG(AAS),
∴CH=FG,
在Rt△CBH和Rt△FEG中,
,
∴Rt△CBH≌Rt△FEG(HL),
∴∠CBA=∠FED,
在△ABC和△EFD中,
,
∴△ABC≌△DEF(AAS).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
