浙江省乐清市育英寄宿学校浙教版九年级数学上册第一章《二次函数》导学案
文档属性
| 名称 | 浙江省乐清市育英寄宿学校浙教版九年级数学上册第一章《二次函数》导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-31 00:00:00 | ||
图片预览




文档简介
1.1 二次函数导学案
班级 学号 姓名
课前预习
1.二次函数的定义:一般的,把形如_________________(其中是常数,____0)的函数叫做二次函数,称为 ,为 ,为__________,其中自变量的取值范围为
2、下列函数中,哪些是二次函数? (填入序号)
(1)错误!未指定书签。(2)(3)(4) (5)
3、分别说出下列二次函数的二次项系数、一次项系数和常数项
(1) (2) (3)
4、关于的函数 是二次函数,求的值.
(注意:二次函数的二次项系数必须是不为零的数)。
5、用待定系数法求二次函数的解析式:二次 ( http: / / www.21cnjy.com )函数y=ax2 +c中,当x=3时,y=26;当x=2时,y=11.则满足条件的二次函数解析式是 。
课堂例题
例1 如图,一张正方形纸板的边长为2cm ( http: / / www.21cnjy.com ),将它剪去4个全等 的直角三角形 (图中阴影部分 )。设AE=BF=CG=DH=x(cm),四边形 EFGH的面积为y(cm2 )
(1)求y关于 x的函数解析式和自变量x的取值范围 ;
(2)当 x分别为0.25,0.5, 1,1.5,1.75时 ,对应的四边形 EFGH的面积,并列表表示.
例2 已知二次函数y=x2 +bx+c,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的表达式.
课后作业
基础达标
1. 在下列函数关系式中,不是二次函数的是( )
A. y=-2x2 B. y=2(x-1)2+3 C. y=(x+3)2-x2 D. y=a(8-a)
2. 在一定条件下,若物体运动的路程s(m)与时间t(s)的关系式为s=5t2 +2t,则当t=4s时,该物体运动的路程为( )
A. 28m B. 48m C. 68m D. 88m
3. 函数y=-(x-2)2+2化为y=ax2+bx+c的形式是 .其中二次项系数是 ,一次项系数是 , 常数项是 .
4. 请写出一个y关于x的二次函数 ,使得函数的二次项系数为1,且当x=1时,y=2.
5. 有n支球队参加比赛,每两队之间进行一场比赛,则比赛的场数m与球队数n之间的关系式是 .
6. 求满足下列条件的二次函数解析式:
二次函数y=ax2 +bx+c中,当x=0时,y=2;当x=1时,y=3;当x=-1时,y=-5.
提高训练
7.若函数 错误!未找到引用源。为二次函数,则m的值为 .
8.观察下面的表格:
x 0 1 2
ax2 2
ax2 +bx+c 4 6
求a,b,c的值,并在表格内的空格中填上正确的数.
9.如图,要建一个三面用木板围成的矩形 ( http: / / www.21cnjy.com )仓库,已知矩形仓库一边靠墙(墙长16 m),并在与墙平行的一边开一道1 m宽的门,现在可围的材料为32 m长的木板,若设与墙平行的一边长为x m,仓库的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x=4时,求y的值.
三、探究创新
10.如图,在正方形ABCD中,AB=4,E是BC上一点,F是CD上一点,且AE=AF,设S△AEF=y,EC=x.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)当△AEF是正三角形时,求△AEF的面积.
1.2二次函数的图象(1)导学案
班级 学号 姓名
课前预习
1.用 画二次函数y=ax2的图象。
2. 二次函数y=ax2(a≠0) ( http: / / www.21cnjy.com )的图象是 ,它关于 对称,顶点是 .当a>0时,抛物线的开口 ,顶点是抛物线上的最低点;当a 0时,抛物线的开口向下, 是抛物线上的最高点.
课堂例题
例1、已知抛物线y=ax2(a≠0)的图像经过点(-2,-3)。
(1)求a的值,并写出这个二次函数的表达式;
(2)说出这个二次函数图像的顶点坐标、对称轴、开口方向和图像的位置.
课后作业
基础达标
1.若二次函数y=ax2的图象经过点(-2,-4),则a的值为 ( )
A. -2 B. 2 C. -1 D. 1
2.二次函数错误!未找到引用源。对称轴是 ,顶点坐标是 ,当x= 时,函数y有最 值,是 .
3.若抛物线y=ax2与抛物线y=2x2关于x轴对称,则a= .
4.关于函数错误!未找到引用源。的性质描述错误的是 ( )
A. 它的图象关于y轴对称 B. 该抛物线开口向下
C. 原点是该抛物线线上的最高点 D. 当x为任意实数时,函数值y总是负数
5.若二次函数错误!未找到引用源。的图象开口向下,则a的取值范围为 ( )
A. 错误!未找到引用源。 B. 错误!未找到引用源。 C. 错误!未找到引用源。 D. 错误!未找到引用源。
6.苹果从树上落下所经过的路程s与下落时间t满足错误!未找到引用源。(g为常数),则s与t的函数图象大致是 ( )
若抛物线y=ax2与直线y=-x交于点(1,m),求m的值及抛物线的解析式.
二、提高训练
8.若二次函数y=ax2的图象开口向上,则直线y=ax+a不经过 ( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
9.抛物线y=-2x2上一点到x轴的距离是2,则该点的横坐标是( )
A. -8 B. 1 C. 1或-1 D. 2或-2
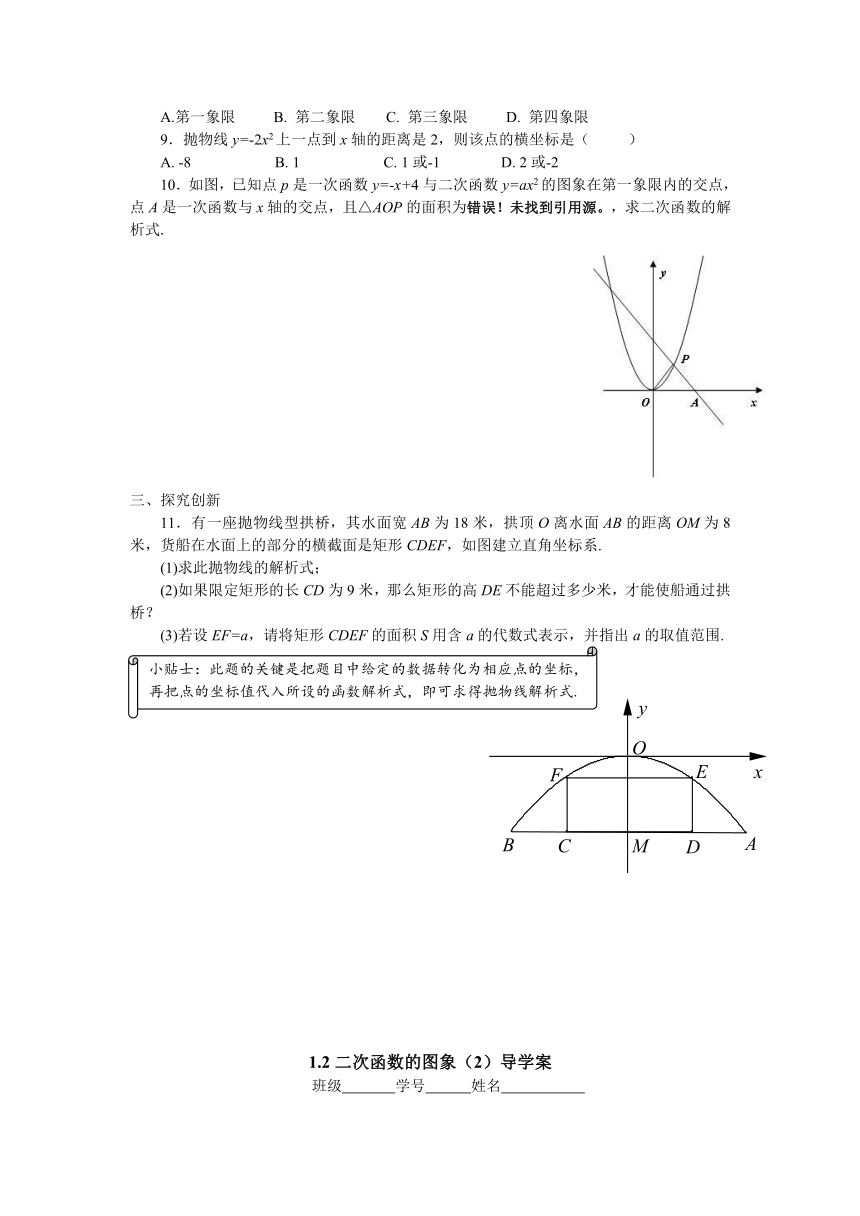
10.如图,已知点p是一次函数y=-x+4与二次函数y=ax2的图象在第一象限内的交点,点A是一次函数与x轴的交点,且△AOP的面积为错误!未找到引用源。,求二次函数的解析式.
三、探究创新
11.有一座抛物线型拱桥,其水面宽 ( http: / / www.21cnjy.com )AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横截面是矩形CDEF,如图建立直角坐标系.
(1)求此抛物线的解析式;
(2)如果限定矩形的长CD为9米,那么矩形的高DE不能超过多少米,才能使船通过拱桥?
(3)若设EF=a,请将矩形CDEF的面积S用含a的代数式表示,并指出a的取值范围.
1.2二次函数的图象(2)导学案
班级 学号 姓名
课前预习
1.用 画二次函数y=a(x+m)2+k的图象。
2. 二次函数y=a(x+m)2+k(a≠0 ( http: / / www.21cnjy.com ))的图象是 ,可以由函数y=ax2的图象先向右(当m<0时)或向左(当m>0时)平移 个单位,再向上(当k>0时)或向下(当k<0时)平移 个单位得到,顶点坐标是 对称轴是直线 . 当a>0时,抛物线的开口 ,顶点是抛物线上的 ;当 时,抛物线的开口向下, 是抛物线上的最高点.
课堂例题
用描点法,在同一直角坐标系中画出函数,,的图像.
1.列自变量与函数的对应值表.
….. . . …..
…… ……
….. …..
…. ….
描点,并用光滑曲线顺次连结各点.
3完成下表.
顶点坐标 对称轴
思考:你能给出()的顶点坐标吗?对称轴呢?
观察三个函数的图像,它们有什么共同特点?有什么不同点?
图像之间的位置能否通过适当 ( http: / / www.21cnjy.com )的变换得到?
根据你的发现,来回答下列问题:
(1)函数的图像,可以由函数的图像向 平移 个单位得到。
(2)函数的图像,可以由函数的图像向 平移 个单位得到。
(3)函数的图像,可以由函数的图像向 平移 个单位得到。
由此你发现了什么?
-----------------------------------------------------------
例1、对于二次函数,请回答下列问题:
①把函数的图像作怎样的平移变换,就能得到函数的图像?
②说出函数的图像的顶点坐标和对称轴。
(1)填空
抛物线 开口方向 对称轴 顶点坐标
y =2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
(2)、填空:
①、由抛物线y=2x 向 平移 个单位可得到y= 2(x+1)2
②、函数y= -5(x -4)2的图象。可以由抛物线 向 平移 4 个单位而得到的。
三、合作学习
用描点法,在同一直角坐标系中画出函数的图像,,, 的图像.
1.列自变量与函数的对应值表.
….. . . …..
…… ……
….. …..
…. ….
2.描点,并用光滑曲线顺次连接.
3.完成下表.
顶点坐标 对称轴
思考:
你能给出()的顶点坐标吗?对称轴呢?
观察三个函数的图像,它们有什么共同特点?有什么不同点?
图像之间的位置能否通过适当的变换得到?
总结出从到平移规律。
---------------------------------------------------
你能总结的图像和图像的关系吗?
----------------------- ------------------------------
课堂训练(一):
1.抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当 时,随的增大而减小;当 时,随的增大而增大。
2. 抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当 时,随的增大而减小;当 时,随的增大而增大。
3.抛物线向右平移4个单位后,得到的抛物线的表达式为______________.
4.将抛物线向右平移1个单位后,得到的抛物线解析式为__________.
5.抛物线向左平移2个单位后,得到的函数关系式是,
则=__________,=___________.
课堂训练(二):
1.抛物线向上平移3个单位,就得到抛物线__________________;
抛物线向下平移4个单位,就得到抛物线__________________.
2.抛物线向上平移3个单位后的解析式为 ,它们的形状__________,当= 时,有最 值是 。
3.函数的图象可由函数的图象沿x轴向 平移 个单位,再沿y轴向 平移 个单位得到。
4.若把函数的图象分别向下、向左移动2个单位,则得到的函数解析式为 。
5. 顶点坐标为(-2,3),开口方向和大小与抛物线相同的解析式为( )
A. B.
C. D.
课堂训练(三):
1、已知一个二次函数图像的形状与抛物线相同,它的顶点坐标是(2,4),
(1)求该二次函数的解析式。
(2)所求二次函数的图像可由抛物线经过怎样的平移得到的?
2、在平面直角坐标系中,二次函数图象的顶点为A(1.,-4),且图像过点B(-2,5)。
(1)求该二次函数的解析式;
(2)求该二次函数的图像与坐标轴的交点坐标;
(3)将该二次函数图象向右平移几个单位,可使平移后所得图像经过坐标原点?并直接写出平移后所的图像与X轴的另外一个交点坐标
1.2二次函数的图像(3)导学案
班级 学号 姓名
课前预习
1.对于二次函数y=ax ( http: / / www.21cnjy.com ) +bx+c (a≠0),其图象的形状、开口方向、位置又是怎样的?通过变形能否将y=ax +bx+c转化为y = a(x+m)2 +k的形式?
y=ax2+bx+c=a( )=错误!未找到引用源。=错误!未找到引用源。
由此可见二次函数y=ax +bx+c的图象与二次函数y=ax 的图象的 、 均相同,只是位置不同,可以通过y=ax 平移得到.
2.请阅读教材中本节内容后回答:
二次函数y=ax +bx+c (a≠0 ( http: / / www.21cnjy.com ))对称轴所处的位置,抛物线与y轴的交点位置,同a、b、c中那几个字母的取值有关?如有,请简单加以说明.
课堂例题
例3、求抛物线的对称轴和顶点坐标。
例4、对于函数,请回答下列问题:
(1)函数的图像能否由函数的图像通过平移得到的?若能,请说出平移的过程,并画出示意图。
(2)函数图像的开口方向、对称轴和顶点坐标。
课后作业
一、基础达标
1.下列函数图像中,经过原点的是( )
A.y=2x+1 B. y=x2-1 C. y=3x2-2x D.y=x2-3x+2
2.已知二次函数y=2x2+bx+c的顶点坐标是(1,-2),则b= ,c= .
3.与抛物线y=-2x2的形状相同,顶点是(-1,3)的二次函数解析式为( )
A. y=-2(x-1)2+3 B. y=±2(x+1)2+3 C. y=±2(x-1)2+3 D. y=-2(x+1)2+3
4.二次函数y=x2+4x+3的图象可以由二次函数y=x2的图像平移得到,下列平移正确的是( )
A.先向左平移两个单位长度,再向上平移一个单位长度
B.先向左平移两个单位长度,再向下平移一个单位长度
C.先向右平移两个单位长度,再向上平移一个单位长度
D.先向右平移两个单位长度,再向下平移一个单位长度
5.如果抛物线y=2x2+4x-c的顶点在x轴上,那么c的值为( )
A.1 B. -1 C. 2 D.-2
6.填表:
函数解析式 对称轴 顶点 可由怎样的y=ax2,经过怎样的平移得到
y=5(x+2)2-3
y=3x2-6x
y=-x2+4x+2
二、提高训练
7.不论a取任何实数,抛物线y=a(x-m)2+m(a≠0)的顶点都在( )
A.直线y=x上 B.直线y=-x上 C. x轴上 D. y轴上
8.二次函数y=ax +bx+c的图象如图所示,则下列结论正确的是( )
A.a>0,b<0, c>0 B. a<0,b<0, c>0
C.a<0,b>0, c<0 D. a<0,b>0, c>0
9.请根据如图所示的已知条件,求出抛物线的解析式,并写出顶点坐标.
三、探究创新
10.如图所示,已知二次函数错误!未找到引用源。的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
1.3 二次函数的性质(1)导学案
班级 学号 姓名
课前预习
当a>0(或a<0)时,当x 时,y随x的大而减小 (或增大),当x 时, y随x的大而增大(或减小).
2.当x 时,y达到最值,y= .
3.抛物线y=ax2+bx+c与b2-4ac的符号有密切的联系,其交点的个数可化分为以下三种:
(1) b2-4ac______0, 与x轴有唯一交点(顶点);(2) b2-4ac______0, 与x轴有两个交点;(3) b2-4ac______0, 与x轴没有交点.
课堂例题
例:已知函数
(1)求函数图像的顶点坐标、对称轴,以及图像和坐标轴的交点坐标,并画出函数的大致图像。
(2)自变量x在什么范围内时,y随x的增大而增大?何时y随x增大而减小?并求出函数的最大值或最小值?
课后作业
一、基础达标
1.当x= 时,二次函数y=2x2+4x+5的最小值是 .
2.若抛物线y=x2+(m-2)x-m与x轴的两个交点关于y轴对称,则m=______.
3.二次函数y=-x2+4x+m的值恒小于0,则m的取值范围是______.
4. 已知抛物线y=-x2+bx+c的x≤0部分的图象如图所示.
(1) 求抛物线的解析式;
(2) 画出当x>0时的抛物线图象;
(3) 利用图象,写出x为何值时,y>0?
5. 已知抛物线y=x2+bx+9经过点(1,2).
(1) 求抛物线的解析式及顶点坐标;
(2) 若点(x1,y1)和点(x2,y2)均在抛物线上,且x1y2,则求x1与x2满足的范围.
二、提高训练
6.已知二次函数y=ax2+2x+c(a≠0)有最大值,且ac=4,则二次函数的顶点在第____象限.
7.如图,抛物线y=ax2+bx+c与x轴相交于点A,B两点,与y轴相交于点C,如果OB=OC=错误!未找到引用源。OA,那么b的值为( )
A.-2 B.-1 C.-错误!未找到引用源。 D.错误!未找到引用源。
8. 如图,已知抛物线y=2x2-4x+m与x轴交于不同的两点A,B,其顶点是C,点D是抛物线的对称轴与x轴的交点.
(1)求实数m的取值范围;
(2) 求顶点C的坐标和线段AB的长度(用含有m的式子表示);
(3)若直线y=错误!未找到引用源。x+1分别与x轴,y轴于点E,F.问△BDC与△EOF是否有可能全等?如果可能,请证明;如果不可能,请说明理由.
三、探究创新
9.已知关于x的二次函数y=x2-mx+错误!未找到引用源。与y=x2-mx-错误!未找到引用源。,这两个二次函数的图象中的一条与x轴交于A,B两个不同的点.
(1)试判断哪个二次函数的图象不能经过A,B两点;
(2)若A点的坐标为(-1,0),试求出B点坐标;
在(2)的条件下,对于经过A,B两点的二次函数,当x为何值时,y随x的增大而减小。
1.4 二次函数的应用(1)导学案
班级 学号 姓名
课前预习
运用二次函数求实际问题中的最大值或 ( http: / / www.21cnjy.com )最小值, 首先应当求出函数 和自变量的 ,再求出它的 ,取得最大值或最小值的相应的自变量的值必须在 内.
课堂例题
例1、图中窗户边框的上半部分是由四个全等 ( http: / / www.21cnjy.com )扇形组成的半圆,下部分是矩形。如果制作一个窗户边框的材料总长为6米,那么如何设计这个窗户边框的尺寸,使透光面积最大(结果精确到0.01m2)
课后作业
基础达标
1. 对于二次函数y=-5x2+8x-1,下列说法中正确的是( )
A. 有最小值2.2 B. 有最大值2.2 C. 有最小值-2.2 D. 有最大值-2
2. 小明用一根长为8cm的细铁丝围成矩形,则矩形的最大面积是( )
A. 4cm2 B. 8cm2 C. 16cm2 D. 32cm2
3.已知二次函数y=(x-1)2+(x-3)2 ,当x= 时,函数达到最小值.
4.已知二次函数y=-x2+mx+2的最大值为错误!未找到引用源。,则m= .
5.某桥梁的两条钢缆具有相同抛物线的形状,两条抛物线关于y轴对称,其中一条抛物线的关系式是错误!未找到引用源。.
(1) 求另一条钢缆的函数关系式;
(2) 求出两条钢缆的最低点之间的距离.
6.如图,在Rt△ABC中,∠C=9 ( http: / / www.21cnjy.com )0°,∠A=30°,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)设四边形DECF的面积为S,求S关于x的函数关系式,并求出S的最大值.
提高训练
7.抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为1,则b的值是_____.
8.如图,ΔABC中,BC=AC=4,∠ACB=120°,点E是AC上一个动点(点E与A,C不重合),ED∥BC,求△CED的最大值.
9.已知抛物线的解析式为y=2x2+3mx+2m,
(1)求该抛物线的顶点坐标(x0,y0);
(2)以x0为自变量,写出y0与x0之间的关系式;
(3)当m为何值时,抛物线的顶点位置最高?
三、探究创新
10.如图,矩形ABCD中,AB=6c ( http: / / www.21cnjy.com )m,BC=12cm.点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动. 若M, N分别从A,B点同时出发,设移动时间为t (0(1) 求S关于t的函数关系式,并求出S的最小值;
(2) 当△DMN为直角三角形时,求△DMN的面积.
1.4 二次函数的应用(2)导学案
班级 学号 姓名
课前预习
1.二次函数是刻画现实生活中某些情境的 .
2.二次函数的应用:(1)求最值(最优化)(2)求最值(距离、利润等)(3)求交点坐标、方程近似解
课堂例题
例2:B船位于A船正东26km处,现在A、B两船同时出发,A船发每小时12km的速度朝正北方向行驶,B船发每小时5km的速度向正西方向行驶,何时两船相距最近?最近距离是多少?
例3、某饮料经营部每天的固定成本为200元,某销售的饮料每瓶进价为5元。
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
(1)若记销售单价比每瓶进价多x元时,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y关于x的函数解析式和自变量的取值范围;
(2)若要使日均毛利润达到最大,销售单价应定为多少元(精确到0.1元)?最大日均毛利润为多少?
课后作业
基础达标
1.小明在某次投篮中,球的运动路线是抛物线错误!未找到引用源。的一部分,如图所示,若命中篮圈中心,则他与篮底的距离L是( )
A. 4.6m B. 4.5m C. 4m D. 3.5m
生产季节性产品的企业,当它的产 ( http: / / www.21cnjy.com )品无利润时就会及时停产. 现有一生产季节性产品的企业,其一年中获得的月利润y与月份n之间函数关系为y=-n2+14n-24,则该企业一年中应停产的月份是( )
A. 1月、2月、3月 B. 2月、3月、4月
C. 1月、2月、12月 D. 1月、11月、12月
3.函数y=x2-4x+3 (-3≤x≤3)的最小值是 , 最大值是 .
4.已知直角三角形的两直角边之和为2,则斜边长可能达到的最小值是 .
5.如图,今有网球从斜坡OA的点O处抛出,网球的抛物路线的函数关系是y=4x-错误!未找到引用源。x2,斜坡的函数关系是y=错误!未找到引用源。x,其中y是垂直高度,x是与点O的水平距离.
(1)求网球到达的最高点B的坐标;
(2)网球落在斜坡上的点A处,写出点A的坐标.
6.我区“联华”超市购进一批20元/千 ( http: / / www.21cnjy.com )克的绿色食品,如果以30元/千克销售,那么每天可售出400千克.由销售经验知,每天销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
(1) 试求出y与x的函数关系式;
(2) 设超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
提高训练
7.函数y=错误!未找到引用源。的最大值是______.
8.二次函数y=ax2+bx+c(a≠0)与x轴的两个交点之间的距离可以用a, b, c的代数表示为错误!未找到引用源。. 请利用以上结论, 求二次函数y=x2+(k+4)x+k的图象与x轴两个交点间的最短距离为 .
探究创新
9.南博汽车城销售某种型号的汽车,每辆进货 ( http: / / www.21cnjy.com )价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.
(1) 求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2) 假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3) 当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
1.4 二次函数的应用(3)导学案
班级 学号 姓名
课前预习
利用解方程ax2+b ( http: / / www.21cnjy.com )x+c=0(a≠O)来求抛物线y=ax2+bx+c(a≠O)与 坐标,也可由y=ax2+bx+c(a≠O)的图象来求一元二次方程ax2+bx+c=0(a≠O)的解.
课堂例题
例4:一个球从地面上竖直向上弹起时的速 ( http: / / www.21cnjy.com )度为10m/s,经过t(s)时求的高度为h(m)。已知物体竖直上抛运动中,h=v0t-gt2(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s2)。问球从弹起至回到地面需多少时间?经多少时间球的高度达到3.75m
结论:从上例我们看到,可以利用解一元二 ( http: / / www.21cnjy.com )次方程求二次函数的图象与横轴(或平行于横轴的直线)的交点坐标。反过来,也可以利用二次函数的图象求一元二次方程的解。
例5、利用二次函数的图象求方程x2+x-1=0的近似解。
课后作业
基础达标
1.若关于x的方程x2-mx+n=0没有实数解,则抛物线y=x2-mx+n与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
2.若x为任意实数时,二次三项式x2-6x+c的值都不小于0,则常数c满足的条件是( )
A. 错误!未找到引用源。≥0 B. c≥9 C. c>0 D. c>9
3.请写出一个经过点(-2,0),(5,0)两点二次函数的表达式_____ _.(写出一个符合要求的即可)
4.已知二次函数y1=ax2+bx+c( ( http: / / www.21cnjy.com )a≠0)与一次函数 y2=kx+m(k≠0) 的图象交于点A(-2,4),B(8,2)(如图所示),则能使 y1>y2成立的x的取值范围是 .
5.已知二次函数y=ax2+bx+c的图象经过(1,0),(6,0),(0,18)三点,直线的解析式为y=3x-3.
(1)求二次函数的解析式;
(2)试说说抛物线与直线的交点情况.
6.某种爆竹点燃后,其上升高度h(米)和时间t(秒)符合关系式: h=v0t错误!未找到引用源。gt2 (0(1) 这种爆竹在地面上点燃后,经过多少时间离地15米?
(2) 在爆竹点燃后的1.5秒至1.8秒这段时间内,判断爆竹是上升或是下降,并说明理由.
提高训练
7.一人乘雪橇沿如图所示的斜坡笔直滑下,滑下 ( http: / / www.21cnjy.com )的距离S(米)与时间t (秒)间的关系式为S=10t+t2,若滑到坡底的时间为2秒,则此人下滑的高度为 .
8.对于二次函数y=ax2+bx+c ( http: / / www.21cnjy.com ) =0(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点,则二次函数y=x2-mx-2(m为实数)的零点有 个.
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出当y>0时,x的取值范围;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
三、探究创新
10.已知二次函数y=x2-(m2+8)x+2(m2+6).
(1)求证:不论m取任何实数,此函数图象都与x轴有两个交点,且两个交点都在x轴的正半轴上;
(2)设这个函数的图象与x轴交于B,C两点,与y轴交于A点,若△ABC的面积为48,求m的值;
(3)设抛物线的顶点为P,是否存在实数m,使△PBC为等腰直角三角形?如果存在,请求出m的值;如果不存在,请说明理由.
A.
B.
C.
D.
小贴士:此题的关键是把题目中给定的数据转化为相应点的坐标,再把点的坐标值代入所设的函数解析式,即可求得抛物线解析式.
(1)
(2)
x=1
y
2
o
x
-1
x
y
O
3
-9
-1
-1
A
B
小贴士:对△DMN的内角分别作直角进行分类讨论.
小贴士:可分别求出二次函数图象与x轴的两个交点坐标.
班级 学号 姓名
课前预习
1.二次函数的定义:一般的,把形如_________________(其中是常数,____0)的函数叫做二次函数,称为 ,为 ,为__________,其中自变量的取值范围为
2、下列函数中,哪些是二次函数? (填入序号)
(1)错误!未指定书签。(2)(3)(4) (5)
3、分别说出下列二次函数的二次项系数、一次项系数和常数项
(1) (2) (3)
4、关于的函数 是二次函数,求的值.
(注意:二次函数的二次项系数必须是不为零的数)。
5、用待定系数法求二次函数的解析式:二次 ( http: / / www.21cnjy.com )函数y=ax2 +c中,当x=3时,y=26;当x=2时,y=11.则满足条件的二次函数解析式是 。
课堂例题
例1 如图,一张正方形纸板的边长为2cm ( http: / / www.21cnjy.com ),将它剪去4个全等 的直角三角形 (图中阴影部分 )。设AE=BF=CG=DH=x(cm),四边形 EFGH的面积为y(cm2 )
(1)求y关于 x的函数解析式和自变量x的取值范围 ;
(2)当 x分别为0.25,0.5, 1,1.5,1.75时 ,对应的四边形 EFGH的面积,并列表表示.
例2 已知二次函数y=x2 +bx+c,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的表达式.
课后作业
基础达标
1. 在下列函数关系式中,不是二次函数的是( )
A. y=-2x2 B. y=2(x-1)2+3 C. y=(x+3)2-x2 D. y=a(8-a)
2. 在一定条件下,若物体运动的路程s(m)与时间t(s)的关系式为s=5t2 +2t,则当t=4s时,该物体运动的路程为( )
A. 28m B. 48m C. 68m D. 88m
3. 函数y=-(x-2)2+2化为y=ax2+bx+c的形式是 .其中二次项系数是 ,一次项系数是 , 常数项是 .
4. 请写出一个y关于x的二次函数 ,使得函数的二次项系数为1,且当x=1时,y=2.
5. 有n支球队参加比赛,每两队之间进行一场比赛,则比赛的场数m与球队数n之间的关系式是 .
6. 求满足下列条件的二次函数解析式:
二次函数y=ax2 +bx+c中,当x=0时,y=2;当x=1时,y=3;当x=-1时,y=-5.
提高训练
7.若函数 错误!未找到引用源。为二次函数,则m的值为 .
8.观察下面的表格:
x 0 1 2
ax2 2
ax2 +bx+c 4 6
求a,b,c的值,并在表格内的空格中填上正确的数.
9.如图,要建一个三面用木板围成的矩形 ( http: / / www.21cnjy.com )仓库,已知矩形仓库一边靠墙(墙长16 m),并在与墙平行的一边开一道1 m宽的门,现在可围的材料为32 m长的木板,若设与墙平行的一边长为x m,仓库的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x=4时,求y的值.
三、探究创新
10.如图,在正方形ABCD中,AB=4,E是BC上一点,F是CD上一点,且AE=AF,设S△AEF=y,EC=x.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)当△AEF是正三角形时,求△AEF的面积.
1.2二次函数的图象(1)导学案
班级 学号 姓名
课前预习
1.用 画二次函数y=ax2的图象。
2. 二次函数y=ax2(a≠0) ( http: / / www.21cnjy.com )的图象是 ,它关于 对称,顶点是 .当a>0时,抛物线的开口 ,顶点是抛物线上的最低点;当a 0时,抛物线的开口向下, 是抛物线上的最高点.
课堂例题
例1、已知抛物线y=ax2(a≠0)的图像经过点(-2,-3)。
(1)求a的值,并写出这个二次函数的表达式;
(2)说出这个二次函数图像的顶点坐标、对称轴、开口方向和图像的位置.
课后作业
基础达标
1.若二次函数y=ax2的图象经过点(-2,-4),则a的值为 ( )
A. -2 B. 2 C. -1 D. 1
2.二次函数错误!未找到引用源。对称轴是 ,顶点坐标是 ,当x= 时,函数y有最 值,是 .
3.若抛物线y=ax2与抛物线y=2x2关于x轴对称,则a= .
4.关于函数错误!未找到引用源。的性质描述错误的是 ( )
A. 它的图象关于y轴对称 B. 该抛物线开口向下
C. 原点是该抛物线线上的最高点 D. 当x为任意实数时,函数值y总是负数
5.若二次函数错误!未找到引用源。的图象开口向下,则a的取值范围为 ( )
A. 错误!未找到引用源。 B. 错误!未找到引用源。 C. 错误!未找到引用源。 D. 错误!未找到引用源。
6.苹果从树上落下所经过的路程s与下落时间t满足错误!未找到引用源。(g为常数),则s与t的函数图象大致是 ( )
若抛物线y=ax2与直线y=-x交于点(1,m),求m的值及抛物线的解析式.
二、提高训练
8.若二次函数y=ax2的图象开口向上,则直线y=ax+a不经过 ( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
9.抛物线y=-2x2上一点到x轴的距离是2,则该点的横坐标是( )
A. -8 B. 1 C. 1或-1 D. 2或-2
10.如图,已知点p是一次函数y=-x+4与二次函数y=ax2的图象在第一象限内的交点,点A是一次函数与x轴的交点,且△AOP的面积为错误!未找到引用源。,求二次函数的解析式.
三、探究创新
11.有一座抛物线型拱桥,其水面宽 ( http: / / www.21cnjy.com )AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横截面是矩形CDEF,如图建立直角坐标系.
(1)求此抛物线的解析式;
(2)如果限定矩形的长CD为9米,那么矩形的高DE不能超过多少米,才能使船通过拱桥?
(3)若设EF=a,请将矩形CDEF的面积S用含a的代数式表示,并指出a的取值范围.
1.2二次函数的图象(2)导学案
班级 学号 姓名
课前预习
1.用 画二次函数y=a(x+m)2+k的图象。
2. 二次函数y=a(x+m)2+k(a≠0 ( http: / / www.21cnjy.com ))的图象是 ,可以由函数y=ax2的图象先向右(当m<0时)或向左(当m>0时)平移 个单位,再向上(当k>0时)或向下(当k<0时)平移 个单位得到,顶点坐标是 对称轴是直线 . 当a>0时,抛物线的开口 ,顶点是抛物线上的 ;当 时,抛物线的开口向下, 是抛物线上的最高点.
课堂例题
用描点法,在同一直角坐标系中画出函数,,的图像.
1.列自变量与函数的对应值表.
….. . . …..
…… ……
….. …..
…. ….
描点,并用光滑曲线顺次连结各点.
3完成下表.
顶点坐标 对称轴
思考:你能给出()的顶点坐标吗?对称轴呢?
观察三个函数的图像,它们有什么共同特点?有什么不同点?
图像之间的位置能否通过适当 ( http: / / www.21cnjy.com )的变换得到?
根据你的发现,来回答下列问题:
(1)函数的图像,可以由函数的图像向 平移 个单位得到。
(2)函数的图像,可以由函数的图像向 平移 个单位得到。
(3)函数的图像,可以由函数的图像向 平移 个单位得到。
由此你发现了什么?
-----------------------------------------------------------
例1、对于二次函数,请回答下列问题:
①把函数的图像作怎样的平移变换,就能得到函数的图像?
②说出函数的图像的顶点坐标和对称轴。
(1)填空
抛物线 开口方向 对称轴 顶点坐标
y =2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
(2)、填空:
①、由抛物线y=2x 向 平移 个单位可得到y= 2(x+1)2
②、函数y= -5(x -4)2的图象。可以由抛物线 向 平移 4 个单位而得到的。
三、合作学习
用描点法,在同一直角坐标系中画出函数的图像,,, 的图像.
1.列自变量与函数的对应值表.
….. . . …..
…… ……
….. …..
…. ….
2.描点,并用光滑曲线顺次连接.
3.完成下表.
顶点坐标 对称轴
思考:
你能给出()的顶点坐标吗?对称轴呢?
观察三个函数的图像,它们有什么共同特点?有什么不同点?
图像之间的位置能否通过适当的变换得到?
总结出从到平移规律。
---------------------------------------------------
你能总结的图像和图像的关系吗?
----------------------- ------------------------------
课堂训练(一):
1.抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当 时,随的增大而减小;当 时,随的增大而增大。
2. 抛物线的开口_______;顶点坐标为_________;对称轴是直线_______;当 时,随的增大而减小;当 时,随的增大而增大。
3.抛物线向右平移4个单位后,得到的抛物线的表达式为______________.
4.将抛物线向右平移1个单位后,得到的抛物线解析式为__________.
5.抛物线向左平移2个单位后,得到的函数关系式是,
则=__________,=___________.
课堂训练(二):
1.抛物线向上平移3个单位,就得到抛物线__________________;
抛物线向下平移4个单位,就得到抛物线__________________.
2.抛物线向上平移3个单位后的解析式为 ,它们的形状__________,当= 时,有最 值是 。
3.函数的图象可由函数的图象沿x轴向 平移 个单位,再沿y轴向 平移 个单位得到。
4.若把函数的图象分别向下、向左移动2个单位,则得到的函数解析式为 。
5. 顶点坐标为(-2,3),开口方向和大小与抛物线相同的解析式为( )
A. B.
C. D.
课堂训练(三):
1、已知一个二次函数图像的形状与抛物线相同,它的顶点坐标是(2,4),
(1)求该二次函数的解析式。
(2)所求二次函数的图像可由抛物线经过怎样的平移得到的?
2、在平面直角坐标系中,二次函数图象的顶点为A(1.,-4),且图像过点B(-2,5)。
(1)求该二次函数的解析式;
(2)求该二次函数的图像与坐标轴的交点坐标;
(3)将该二次函数图象向右平移几个单位,可使平移后所得图像经过坐标原点?并直接写出平移后所的图像与X轴的另外一个交点坐标
1.2二次函数的图像(3)导学案
班级 学号 姓名
课前预习
1.对于二次函数y=ax ( http: / / www.21cnjy.com ) +bx+c (a≠0),其图象的形状、开口方向、位置又是怎样的?通过变形能否将y=ax +bx+c转化为y = a(x+m)2 +k的形式?
y=ax2+bx+c=a( )=错误!未找到引用源。=错误!未找到引用源。
由此可见二次函数y=ax +bx+c的图象与二次函数y=ax 的图象的 、 均相同,只是位置不同,可以通过y=ax 平移得到.
2.请阅读教材中本节内容后回答:
二次函数y=ax +bx+c (a≠0 ( http: / / www.21cnjy.com ))对称轴所处的位置,抛物线与y轴的交点位置,同a、b、c中那几个字母的取值有关?如有,请简单加以说明.
课堂例题
例3、求抛物线的对称轴和顶点坐标。
例4、对于函数,请回答下列问题:
(1)函数的图像能否由函数的图像通过平移得到的?若能,请说出平移的过程,并画出示意图。
(2)函数图像的开口方向、对称轴和顶点坐标。
课后作业
一、基础达标
1.下列函数图像中,经过原点的是( )
A.y=2x+1 B. y=x2-1 C. y=3x2-2x D.y=x2-3x+2
2.已知二次函数y=2x2+bx+c的顶点坐标是(1,-2),则b= ,c= .
3.与抛物线y=-2x2的形状相同,顶点是(-1,3)的二次函数解析式为( )
A. y=-2(x-1)2+3 B. y=±2(x+1)2+3 C. y=±2(x-1)2+3 D. y=-2(x+1)2+3
4.二次函数y=x2+4x+3的图象可以由二次函数y=x2的图像平移得到,下列平移正确的是( )
A.先向左平移两个单位长度,再向上平移一个单位长度
B.先向左平移两个单位长度,再向下平移一个单位长度
C.先向右平移两个单位长度,再向上平移一个单位长度
D.先向右平移两个单位长度,再向下平移一个单位长度
5.如果抛物线y=2x2+4x-c的顶点在x轴上,那么c的值为( )
A.1 B. -1 C. 2 D.-2
6.填表:
函数解析式 对称轴 顶点 可由怎样的y=ax2,经过怎样的平移得到
y=5(x+2)2-3
y=3x2-6x
y=-x2+4x+2
二、提高训练
7.不论a取任何实数,抛物线y=a(x-m)2+m(a≠0)的顶点都在( )
A.直线y=x上 B.直线y=-x上 C. x轴上 D. y轴上
8.二次函数y=ax +bx+c的图象如图所示,则下列结论正确的是( )
A.a>0,b<0, c>0 B. a<0,b<0, c>0
C.a<0,b>0, c<0 D. a<0,b>0, c>0
9.请根据如图所示的已知条件,求出抛物线的解析式,并写出顶点坐标.
三、探究创新
10.如图所示,已知二次函数错误!未找到引用源。的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
1.3 二次函数的性质(1)导学案
班级 学号 姓名
课前预习
当a>0(或a<0)时,当x 时,y随x的大而减小 (或增大),当x 时, y随x的大而增大(或减小).
2.当x 时,y达到最值,y= .
3.抛物线y=ax2+bx+c与b2-4ac的符号有密切的联系,其交点的个数可化分为以下三种:
(1) b2-4ac______0, 与x轴有唯一交点(顶点);(2) b2-4ac______0, 与x轴有两个交点;(3) b2-4ac______0, 与x轴没有交点.
课堂例题
例:已知函数
(1)求函数图像的顶点坐标、对称轴,以及图像和坐标轴的交点坐标,并画出函数的大致图像。
(2)自变量x在什么范围内时,y随x的增大而增大?何时y随x增大而减小?并求出函数的最大值或最小值?
课后作业
一、基础达标
1.当x= 时,二次函数y=2x2+4x+5的最小值是 .
2.若抛物线y=x2+(m-2)x-m与x轴的两个交点关于y轴对称,则m=______.
3.二次函数y=-x2+4x+m的值恒小于0,则m的取值范围是______.
4. 已知抛物线y=-x2+bx+c的x≤0部分的图象如图所示.
(1) 求抛物线的解析式;
(2) 画出当x>0时的抛物线图象;
(3) 利用图象,写出x为何值时,y>0?
5. 已知抛物线y=x2+bx+9经过点(1,2).
(1) 求抛物线的解析式及顶点坐标;
(2) 若点(x1,y1)和点(x2,y2)均在抛物线上,且x1
二、提高训练
6.已知二次函数y=ax2+2x+c(a≠0)有最大值,且ac=4,则二次函数的顶点在第____象限.
7.如图,抛物线y=ax2+bx+c与x轴相交于点A,B两点,与y轴相交于点C,如果OB=OC=错误!未找到引用源。OA,那么b的值为( )
A.-2 B.-1 C.-错误!未找到引用源。 D.错误!未找到引用源。
8. 如图,已知抛物线y=2x2-4x+m与x轴交于不同的两点A,B,其顶点是C,点D是抛物线的对称轴与x轴的交点.
(1)求实数m的取值范围;
(2) 求顶点C的坐标和线段AB的长度(用含有m的式子表示);
(3)若直线y=错误!未找到引用源。x+1分别与x轴,y轴于点E,F.问△BDC与△EOF是否有可能全等?如果可能,请证明;如果不可能,请说明理由.
三、探究创新
9.已知关于x的二次函数y=x2-mx+错误!未找到引用源。与y=x2-mx-错误!未找到引用源。,这两个二次函数的图象中的一条与x轴交于A,B两个不同的点.
(1)试判断哪个二次函数的图象不能经过A,B两点;
(2)若A点的坐标为(-1,0),试求出B点坐标;
在(2)的条件下,对于经过A,B两点的二次函数,当x为何值时,y随x的增大而减小。
1.4 二次函数的应用(1)导学案
班级 学号 姓名
课前预习
运用二次函数求实际问题中的最大值或 ( http: / / www.21cnjy.com )最小值, 首先应当求出函数 和自变量的 ,再求出它的 ,取得最大值或最小值的相应的自变量的值必须在 内.
课堂例题
例1、图中窗户边框的上半部分是由四个全等 ( http: / / www.21cnjy.com )扇形组成的半圆,下部分是矩形。如果制作一个窗户边框的材料总长为6米,那么如何设计这个窗户边框的尺寸,使透光面积最大(结果精确到0.01m2)
课后作业
基础达标
1. 对于二次函数y=-5x2+8x-1,下列说法中正确的是( )
A. 有最小值2.2 B. 有最大值2.2 C. 有最小值-2.2 D. 有最大值-2
2. 小明用一根长为8cm的细铁丝围成矩形,则矩形的最大面积是( )
A. 4cm2 B. 8cm2 C. 16cm2 D. 32cm2
3.已知二次函数y=(x-1)2+(x-3)2 ,当x= 时,函数达到最小值.
4.已知二次函数y=-x2+mx+2的最大值为错误!未找到引用源。,则m= .
5.某桥梁的两条钢缆具有相同抛物线的形状,两条抛物线关于y轴对称,其中一条抛物线的关系式是错误!未找到引用源。.
(1) 求另一条钢缆的函数关系式;
(2) 求出两条钢缆的最低点之间的距离.
6.如图,在Rt△ABC中,∠C=9 ( http: / / www.21cnjy.com )0°,∠A=30°,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)设四边形DECF的面积为S,求S关于x的函数关系式,并求出S的最大值.
提高训练
7.抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为1,则b的值是_____.
8.如图,ΔABC中,BC=AC=4,∠ACB=120°,点E是AC上一个动点(点E与A,C不重合),ED∥BC,求△CED的最大值.
9.已知抛物线的解析式为y=2x2+3mx+2m,
(1)求该抛物线的顶点坐标(x0,y0);
(2)以x0为自变量,写出y0与x0之间的关系式;
(3)当m为何值时,抛物线的顶点位置最高?
三、探究创新
10.如图,矩形ABCD中,AB=6c ( http: / / www.21cnjy.com )m,BC=12cm.点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动. 若M, N分别从A,B点同时出发,设移动时间为t (0
(2) 当△DMN为直角三角形时,求△DMN的面积.
1.4 二次函数的应用(2)导学案
班级 学号 姓名
课前预习
1.二次函数是刻画现实生活中某些情境的 .
2.二次函数的应用:(1)求最值(最优化)(2)求最值(距离、利润等)(3)求交点坐标、方程近似解
课堂例题
例2:B船位于A船正东26km处,现在A、B两船同时出发,A船发每小时12km的速度朝正北方向行驶,B船发每小时5km的速度向正西方向行驶,何时两船相距最近?最近距离是多少?
例3、某饮料经营部每天的固定成本为200元,某销售的饮料每瓶进价为5元。
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
(1)若记销售单价比每瓶进价多x元时,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y关于x的函数解析式和自变量的取值范围;
(2)若要使日均毛利润达到最大,销售单价应定为多少元(精确到0.1元)?最大日均毛利润为多少?
课后作业
基础达标
1.小明在某次投篮中,球的运动路线是抛物线错误!未找到引用源。的一部分,如图所示,若命中篮圈中心,则他与篮底的距离L是( )
A. 4.6m B. 4.5m C. 4m D. 3.5m
生产季节性产品的企业,当它的产 ( http: / / www.21cnjy.com )品无利润时就会及时停产. 现有一生产季节性产品的企业,其一年中获得的月利润y与月份n之间函数关系为y=-n2+14n-24,则该企业一年中应停产的月份是( )
A. 1月、2月、3月 B. 2月、3月、4月
C. 1月、2月、12月 D. 1月、11月、12月
3.函数y=x2-4x+3 (-3≤x≤3)的最小值是 , 最大值是 .
4.已知直角三角形的两直角边之和为2,则斜边长可能达到的最小值是 .
5.如图,今有网球从斜坡OA的点O处抛出,网球的抛物路线的函数关系是y=4x-错误!未找到引用源。x2,斜坡的函数关系是y=错误!未找到引用源。x,其中y是垂直高度,x是与点O的水平距离.
(1)求网球到达的最高点B的坐标;
(2)网球落在斜坡上的点A处,写出点A的坐标.
6.我区“联华”超市购进一批20元/千 ( http: / / www.21cnjy.com )克的绿色食品,如果以30元/千克销售,那么每天可售出400千克.由销售经验知,每天销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
(1) 试求出y与x的函数关系式;
(2) 设超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
提高训练
7.函数y=错误!未找到引用源。的最大值是______.
8.二次函数y=ax2+bx+c(a≠0)与x轴的两个交点之间的距离可以用a, b, c的代数表示为错误!未找到引用源。. 请利用以上结论, 求二次函数y=x2+(k+4)x+k的图象与x轴两个交点间的最短距离为 .
探究创新
9.南博汽车城销售某种型号的汽车,每辆进货 ( http: / / www.21cnjy.com )价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.
(1) 求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2) 假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3) 当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
1.4 二次函数的应用(3)导学案
班级 学号 姓名
课前预习
利用解方程ax2+b ( http: / / www.21cnjy.com )x+c=0(a≠O)来求抛物线y=ax2+bx+c(a≠O)与 坐标,也可由y=ax2+bx+c(a≠O)的图象来求一元二次方程ax2+bx+c=0(a≠O)的解.
课堂例题
例4:一个球从地面上竖直向上弹起时的速 ( http: / / www.21cnjy.com )度为10m/s,经过t(s)时求的高度为h(m)。已知物体竖直上抛运动中,h=v0t-gt2(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s2)。问球从弹起至回到地面需多少时间?经多少时间球的高度达到3.75m
结论:从上例我们看到,可以利用解一元二 ( http: / / www.21cnjy.com )次方程求二次函数的图象与横轴(或平行于横轴的直线)的交点坐标。反过来,也可以利用二次函数的图象求一元二次方程的解。
例5、利用二次函数的图象求方程x2+x-1=0的近似解。
课后作业
基础达标
1.若关于x的方程x2-mx+n=0没有实数解,则抛物线y=x2-mx+n与x轴的交点个数为( )
A. 2个 B. 1个 C. 0个 D. 不能确定
2.若x为任意实数时,二次三项式x2-6x+c的值都不小于0,则常数c满足的条件是( )
A. 错误!未找到引用源。≥0 B. c≥9 C. c>0 D. c>9
3.请写出一个经过点(-2,0),(5,0)两点二次函数的表达式_____ _.(写出一个符合要求的即可)
4.已知二次函数y1=ax2+bx+c( ( http: / / www.21cnjy.com )a≠0)与一次函数 y2=kx+m(k≠0) 的图象交于点A(-2,4),B(8,2)(如图所示),则能使 y1>y2成立的x的取值范围是 .
5.已知二次函数y=ax2+bx+c的图象经过(1,0),(6,0),(0,18)三点,直线的解析式为y=3x-3.
(1)求二次函数的解析式;
(2)试说说抛物线与直线的交点情况.
6.某种爆竹点燃后,其上升高度h(米)和时间t(秒)符合关系式: h=v0t错误!未找到引用源。gt2 (0
(2) 在爆竹点燃后的1.5秒至1.8秒这段时间内,判断爆竹是上升或是下降,并说明理由.
提高训练
7.一人乘雪橇沿如图所示的斜坡笔直滑下,滑下 ( http: / / www.21cnjy.com )的距离S(米)与时间t (秒)间的关系式为S=10t+t2,若滑到坡底的时间为2秒,则此人下滑的高度为 .
8.对于二次函数y=ax2+bx+c ( http: / / www.21cnjy.com ) =0(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点,则二次函数y=x2-mx-2(m为实数)的零点有 个.
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出当y>0时,x的取值范围;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
三、探究创新
10.已知二次函数y=x2-(m2+8)x+2(m2+6).
(1)求证:不论m取任何实数,此函数图象都与x轴有两个交点,且两个交点都在x轴的正半轴上;
(2)设这个函数的图象与x轴交于B,C两点,与y轴交于A点,若△ABC的面积为48,求m的值;
(3)设抛物线的顶点为P,是否存在实数m,使△PBC为等腰直角三角形?如果存在,请求出m的值;如果不存在,请说明理由.
A.
B.
C.
D.
小贴士:此题的关键是把题目中给定的数据转化为相应点的坐标,再把点的坐标值代入所设的函数解析式,即可求得抛物线解析式.
(1)
(2)
x=1
y
2
o
x
-1
x
y
O
3
-9
-1
-1
A
B
小贴士:对△DMN的内角分别作直角进行分类讨论.
小贴士:可分别求出二次函数图象与x轴的两个交点坐标.
同课章节目录
