九年级数学上册试题 4.5 相似三角形的性质及其应用-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.5 相似三角形的性质及其应用-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 971.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-08 23:35:58 | ||
图片预览

文档简介
4.5 相似三角形的性质及其应用
一、单选题
1.若的面积是,则它的三条中位线围成的三角形的面积是( )
A. B. C. D.无法确定
2.如图,矩形中,,,点P在对角线上,且,连接并延长,交的延长线于点Q,连接,则的长为( )
A. B. C. D.
3.如图,ABC中,DE∥BC,AD:BD=1:3,则OE:OB=( )
A.1:3 B.1:4 C.1:5 D.1:6
4.如图,在矩形中,是的中点,若交于点,是的中点,连接,,则的长为( )
A. B. C.1 D.
5.如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为( )
A. B. C. D.
6.如图,在平行四边形ABCD中,点E是AD上一点,,连接BE交AC于点G,延长BE交CD的延长线于点F,则的值为( )
A. B. C. D.
7.如图,中,,是中线, 是上一点,作射线,交于点,若,则 ( )
A. B. C. D.
8.小明想借助网格在线段AB上找一点P,使AP∶PB=2∶3,下列作法中错误的是( )
A. B.
C. D.
9.如图,在△ABC中,AB=AC,点D是BC边的中点,点E是AB边的中点,过点E作EF∥AD交BC于点F,过点E作EG∥BC交AD于点G,设△ABC的面积为S,则四边形EFDG的面积为( )
A.S B.S C.S D.S
10.直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A. B. C. D.
二、填空题
11.在△ABC和△DEF中,∠A=∠D=105°,AC=4cm,AB=6cm,DE=3cm,则DF=_________时,△ABC与△DEF相似.
12.如图,已知矩形ABCD中,AB=6,AD=8将矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,如果AE=2AM,那么CN的长为______.
13.如图,四边形中,对角线交于点O,,,,,如果,那么的值是___________.
14.如图,在平面直角坐标系中,与轴交于点,已知点,,,是线段上一点,连接,若与相似,则的长为______.
15.如图,在矩形ABCD中,点E在边BC上,连结AE,将△ABE沿直线AE翻折得到△AFE,EF与AC相交于点M.若AB=8,BC=10,且BE=BC,则点F到直线AD的距离为____.
16.如图,矩形ABCD沿EF折叠,点A的对称点为点A',点B的对称点为点B',A'B'与AD相交于点G,若点F,B',D在同一条直线上,△A'EG的面积为4,△CDF的面积为36,则△GB'D的面积等于______.
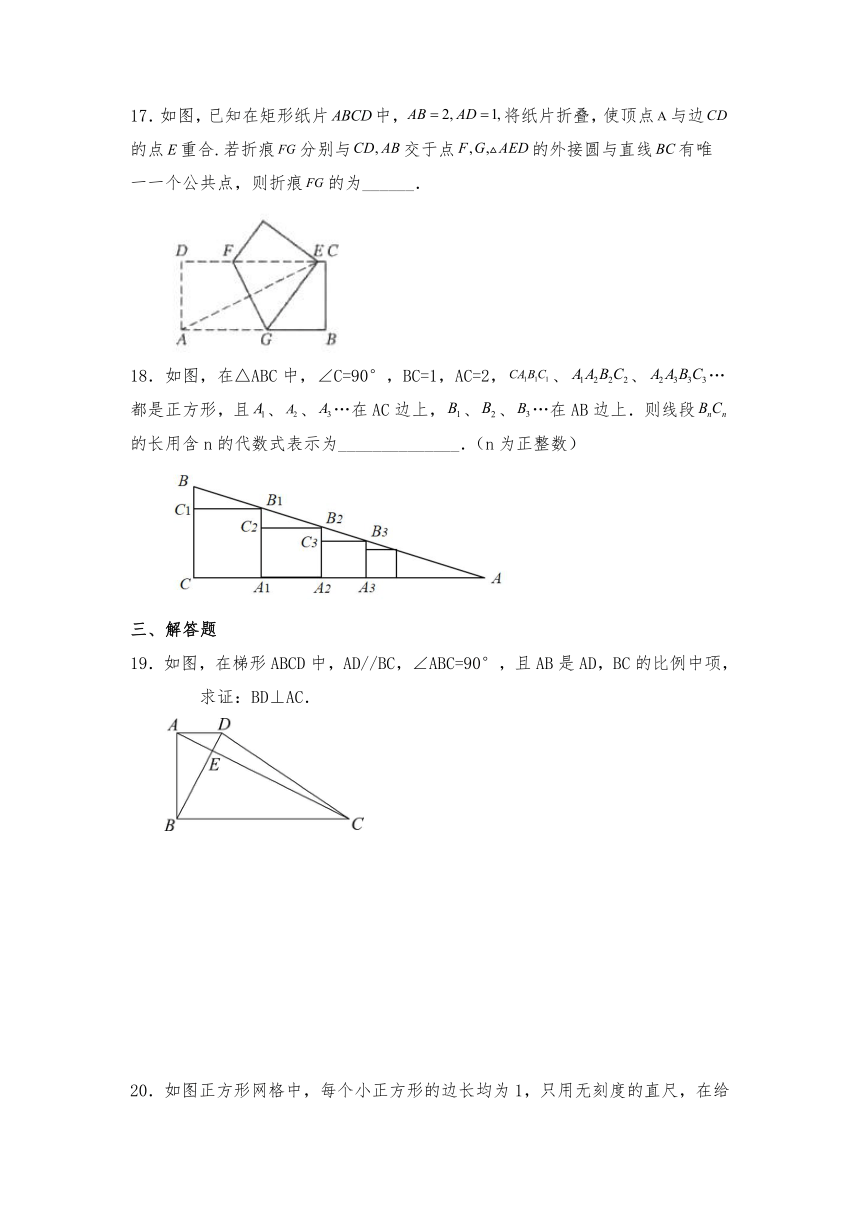
17.如图,已知在矩形纸片中,将纸片折叠,使顶点与边的点重合.若折痕分别与交于点的外接圆与直线有唯一一个公共点,则折痕的为______.
18.如图,在△ABC中,∠C=90°,BC=1,AC=2,、、…都是正方形,且、、…在AC边上,、、…在AB边上.则线段的长用含n的代数式表示为______________.(n为正整数)
三、解答题
19.如图,在梯形ABCD中,AD//BC,∠ABC=90°,且AB是AD,BC的比例中项,
求证:BD⊥AC.
20.如图正方形网格中,每个小正方形的边长均为1,只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中画等腰△ABC,使得∠CAB=90°;
(2)在图②中画等腰△DEF,使△ABC∽△DEF,且相似比为:1.
21.如图,△ABC中,点D,E分别是BC,AB上的点,CE,AD交于点 F,BD=AD,BE=EC.
求证:△ABD∽△CBE;
若CD=CF,试求∠ABC的度数.
22.如图,已知点在轴的负半轴上,点在轴的正半轴上,,,点在线段上,从点出发以每秒5个单位长度的速度向点运动,设运动时间为秒,过点作轴于点.
(1) 当时,线段的长为________;
(2) 当时,求的值;
(3) 在轴上是否存在点,使为等腰三角形,若存在,直接写出点的坐标,若不存在,说明理由.
23.在菱形中,,点、分别是边、上两点,满足,与相交于点.
(1)如图1,连接.求证:;
(2)如图2,连接.
① 求证:;
② 若,,求线段的长(用含、的代数式表示).
24.如图1,在等腰中,,点D为斜边AB边上一动点(不含端点).作,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
【问题发现】
(1)如图1,若点D为BC边中点.请直接写出DE,DF的数量关系_________.
【类比探究】
(2)如图2,若点D为BC边上一动点,且.猜想DF与DE的数量关系.并证明你的结论.
【拓展应用】
(3)如图3,在边长为4的等边中,点D为BC边上一动点,作.DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.
答案
一、单选题
1.A
【分析】
根据三角形中位线定理即可证得:,则△DEF∽△ABC,根据相似三角形的面积的比等于相似比的平方即可求解.
解:如图:
∵DE是△ABC的中位线,
∴DE=BC,即,
同理,,,
∴,
∴△DEF∽△ABC,
∴,
∴S△DEF=S△ABC=×8=2(cm2).
故选:A.
2.C
【分析】
根据矩形的性质可求BD,,从而得到QC,由勾股定理即可求解;
解:∵在矩形中,,,
∴
∵AB∥CD,
∴
∵
∴
∵
∴
∴
∴
故选:C.
3.B
【分析】
先根据DE∥BC,得出ADE∽ABC,进而得出 ,再根据DE∥BC,得到ODE∽OCB,进而得到.
解:∵DE∥BC,
∴ADE∽ABC,
∴,
又∵,
∴,
∵DE∥BC,
∴ODE∽OCB,
∴.
故选:B.
4.C
【分析】
先证明,可得3EF=,延长AE交DC得延长线于点H,可得,继而即可求解.
解:∵在矩形中,
∴AD∥BC,AD=BC,
∴,
∴,即:3EF=,
延长AE交DC得延长线于点H,
∵AB∥CD,
∴∠ABE=∠HCE=90°,
∵是的中点,
∴BE=CE,
又∵∠AEB=∠CEH,
∴,
∴AE=EH,AB=CH=CD,即C是DH的中点,
∵是的中点,
∴HF=2,
∵3EF=,
∴4EF=4,
∴EF=1,
故选C.
5.B
【分析】
根据题意,画出示意图,易得△EDC∽△FDC,进而可得,即DC2=ED FD,代入数据可得答案.
解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又
∴△EDC∽△CDF,
∴,即DC2=ED FD=2×8=16,
解得CD=4m(负值舍去).
故选:B.
6.A
【分析】
先根据平行四边形的性质得到AB∥CD,则可判断△ABG∽△CFG,△ABE∽△DFE,于是根据相似三角形的性质和AE=2ED即可得结果.
解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△ABG∽△CFG,
∴=
∵△ABE∽△DFE,
∴=,
∵AE=2ED,
∴AB=2DF,
∴=,
∴=.
故选:A.
7.C
【分析】
作,交于点,则有,根据 ,,可得,,再根据是边上的中线,得到,;根据可得,则,化简即可得到结果.
解:如图,作,交于点,
∴
∴,
又∵,,
∴,
∴,
∴
∵是边上的中线,
∴
∴,
∴,
∵
∴
∴
∴,
则.
故选:C.
8.D
【分析】
利用平行可证得三角形相似,再利用相似三角形的对应边成比例,对各选项逐一判断.
解:A、根据图形,可知两个三角形相似,且相似比为2∶3,故AP∶PB=2∶3,故正确,故此选项不符合题意.
B、根据图形,可知两个三角形相似,且相似比为2∶3,故AP:PB=2∶3,故正确,故此选项不符合题意.
C、如图,
根据图形可知:∠CAD=90°,线段CD绕点O顺时针旋转90°与AB重合,则∠APC=旋转角=90°=∠CAD,∠ACD=∠DCA,
∴△ACD∽△DCA,
∴,
∵AC=,AD=2, CD=,
∴AP=,
∵S△BCD=,
∴BP=,故AP∶PB=2∶3,故正确,故此选项不符合题意.
D、可知两个三角形不相似,故AP:PB之比无法判断,故错误,故此选项符合题意.
故答案为:D.
9.B
【分析】
根据等腰三角形的性质可得AD⊥BC,BDBC,然后可得四边形EFDG是矩形,再根据三角形中位线定理可得EGBDBC,DG=AGAD,进而可以解决问题.
解:∵AB=AC,点D是BC边的中点,
∴AD⊥BC,BDBC,
∴∠ADB=90°,
∵EF∥AD,EG∥BC,
∴四边形EFDG是平行四边形,
又∠ADB=90°,
∴四边形EFDG是矩形,
∵点E是AB边的中点,
∴AE=BE,
∴AG=DG,
∴EG是△ABD的中位线,
∴EGBDBC,DG=AGAD,
∵△ABC的面积为S,
∴SBC AD,
∴四边形EFDG的面积=FD DGBCADS.
故选:B.
10.A
【分析】
分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,可得AF=4,先根据全等三角形的判定定理得出△BCE≌△CAF,故可得出CF及CE的长,在Rt△ACF中根据勾股定理求出AC的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD的长,在Rt△BCD中根据勾股定理即可求出BD的长.
解:分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,垂足为F、E、G,
∵l1与l2的距离为1,l2与l3的距离为3,
∴AF=4,BE=DG=3,
∵△ABC是等腰直角三角形,
∴AC=BC,
∵∠EBC+∠BCE=90°,∠BCE+∠FCA=90°,∠FCA+∠CAF=90°,
∴∠EBC=∠FCA,∠BCE=∠CAF,
在△BCE与△ACF中,,
∴△BCE≌△CAF,
∴CF=BE=3,
∴AC==5,
∵AF⊥l3,DG⊥l3,
∴△CDG∽△CAF,
∴,即,
解得:CD=,
∴BD==.
故选:A.
二、填空题
11.或
【分析】
由于两相似三角形的对应边不能确定,故应分△ABC∽△DEF与△ABC∽△DFE两种情况进行讨论.
解:∵∠A=∠D,AB=6cm,AC=4cm,DE=3cm,
∴当△ABC∽△DEF时,=,即,
解得:DF=2;
当△ABC∽△DFE时,=,
即,
解得:DF=4.5.
综上所述,当DF=2cm或4.5cm时,△ABC和△DEF相似.
故答案为:2cm或4.5cm.
12.
【分析】
如图,过N作NF⊥AD于F,可得NF=AB,根据矩形的性质和折叠的性质可得∠MEN=∠B=90°,EN=BN,根据直角三角形两锐角互余的性质及平角的定义可得∠AME=∠NEF,进而可证明△AEM∽△FNE,根据AE=2AM可求出EF的长,在Rt△FNE中,利用勾股定理可求出EN的长,进而可求出CN的长.
解:如图,过N作NF⊥AD于F,
∵四边形ABCD是矩形,AB=6,
∴NF=AB=6,
∵矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,
∴EN=BN,∠MEN=∠B=90°,
∴∠AEM+∠NEF=90°,
∵∠AEM+∠AME=90°,
∴∠AME=∠NEF,
又∵∠A=∠EFN=90°,
∴△AEM∽△FNE,
∴,
∵AE=2AM,NF=6,
∴EF=3,
∴BN=EN===,
∵BC=8,
∴CN=BC-BN=8-,
故答案为:8-
13.
【分析】
由题意可以证得△AOD∽△BOC,再根据相似三角形的性质得到AO:OD=BO:OC,从而得到△AOB∽△DOC,最后再根据相似三角形的性质得到解答.
解:在△AOD和△BOC中,,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴AO:OB=DO:OC=AD:BC=1:2,
∴OB=4,DO=3,
∴在△AOB和△DOC中,∠AOB=∠DOC,AO:OD=BO:OC=2:3,
∴△AOB∽△DOC,
∴= AO:OD=2:3,
故答案为.
14.2或4
【分析】
是一个直角三角形,若与相似,必须证明是直角三角形,再用相似三角形的性质即可求出点M的坐标.
解:如图,
∵A(1,4) , C(3,0) , D(0,3) ,
∴ ,,,
;
∴是直角三角形
∵点M在x轴上,设点M的坐标是(x,0),
∽
∴
∴=1
∴
当时,CM=2;当时CM=4,
故答案为:2或4.
15..
【分析】
先过F作MN⊥BC,根据已知条件与折叠的性质得到△AFN∽△FEM,再根据相似的性质得到,设出未知数,求解出答案即可.
解:过F作MN⊥BC,
∵BE=,BC=10,
∴BE=6,
∵翻折
∴△ABE≌△AFE,
∴EF=BE=6,∠AFE=∠B=90°,AF= AB=8,
∴∠AFN+∠EFM=90°,
∵∠AFN+∠FAN=90°,
∴∠FAN=∠EFM,
∴△AFN∽△FEM,
∴,
设AN=4x,FM=3x, FN=8-3x,EM=4x-6,
∴FN=8-3x,EM=4x-6,
∴,
∴,
经检验:是原方程的根,
∴,
故答案为:.
16.16
【分析】
由矩形ABCD沿EF折叠, 可得∠A′=∠A =90°,A′B′=AB,可证A′E∥DF,可得∠A′EG=∠GDB′,可证△A′EG∽△CFD,可得,可证△A′EG∽△B′DG,即可.
解:∵矩形ABCD沿EF折叠,点A的对称点为点A',点B的对称点为点B',
∴∠A′=∠A=∠A′B′F=∠B=∠C=90°,A′B′=AB,
∵∠A′+∠A′B′F=180°,
∴A′E∥DF,
∴∠A′EG=∠GDB′,
∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,
∴∠GDB′=∠DFC=∠A′EG,
∴△A′EG∽△CFD,
∴,
∴即,
∴,
∵∠A′=∠A′B′F=90°,∠A′EG=∠GDB′,
∴△A′EG∽△B′DG,
,
∵S△A'EG=4,
∴.
故答案为:16.
17.
【分析】
根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而判断出EF=AG,得出四边形AGEF是平行四边形,继而结合AG=GE,判定四边形AGEF是菱形;连接ON,得出ON是梯形ABCE的中位线,在RT△ADE中,利用勾股定理可解出x,继而可得出折痕FG的长度.
解:由折叠的性质可得,GA=GE,∠AGF=∠EGF,
∵DC∥AB,
∴∠EFG=∠AGF,
∴∠EFG=∠EGF,
∴EF=EG=AG,
∴四边形AGEF是平行四边形(EF∥AG,EF=AG),
又∵AG=GE,
∴四边形AGEF是菱形
令△AED的外接圆与直线有唯一一个公共点为N,连接ON,如图所示,
∵△AED是直角三角形,AE是斜边,点O是AE的中点,△AED的外接圆与BC相切于点N,
∴ON⊥BC,
∵点O是AE的中点,
∴ON是梯形ABCE的中位线,
设CE=x,则ED=2-x,2ON=CE+AB=x+2,
在Rt△AED中,AE=2OE=2ON=x+2,
AD2+DE2=AE2,
∴12+(2-x)2=(2+x)2,
得x=,
,
∵△FEO∽△AED,
∴,
解得:FO=,
∴FG=2FO=.
故答案为:.
18.
【分析】
根据题意得出△BB1C1∽△BAC,进而求出B1C1=,同理可得出:B2C2=,B3C3=,…,进而得出答案.
解:由题意可得:B1C1//AC,
∴△BB1C1∽△BAC,
∴BC1:BC=B1C1:AC,
∵CC1=B1C1,
∴B1C1:2=(1 C1B1):1,
解得:B1C1=,
故A1B1=,AA1=,
同理可得出:B2C2=,B3C3=,…,
∴线段BnCn的长用含n的代数式表示为:.
故答案为:.
三、解答题
19.
解:∵AD∥BC,∠ABC=90°,
∴∠BAD=90°,
∵AB是AD,BC的比例中项,
即AB2=AD BC,
∴
而∠ABC=∠DAB,
∴△ABC∽△DAB,
∴∠ABD=∠ACB,
∵∠ABD+∠DBC=90°,
∴∠ACB+∠DBC=90°,
∴∠BEC=90°,
∴BD⊥AC.
20.
解:(1)如图①中,△ABC即为所求;
,,,
,
,
的等腰直角三角形,
(2)如图②中,△DEF即为所求.
,,,
,
.
△ABC∽△DEF,且相似比为:1.
21.
(1)证明:∵BD=AD,BE=EC
∴∠B=∠BAD,∠B=∠BCE
∴∠BAD=∠BCE
而∠B=∠B,
∴△ABD∽△CBE
(2)解:设∠B=,由(1)可知∠B=∠BAD=∠BCE=,
∴∠ADC=
又∵CD=CF
∴∠ADC=∠DFC=
∴
∴
即
22.
(1)解:由题意可得:当时,PA=PB,且PQ∥AO,
∴,BQ=QO,
∴PQ为三角形ABO的中位线,
∴PQ=AO=,
故答案为;
(2)解:由题可知,PA=PQ=5t, ∴ PB=AB-PA=5-5t
∵PQ∥AO ∴∠BPQ=∠BAO
又∵BQP=∠BOA=90°
∴△BPQ∽△BAO
∴ 解得:t=
(3)解:由题意可设满足条件的M为(x,0),则可分三种情况:
如图,MA=MB,
则MA2=MB2,
∴(x+3)2=OM2+OB2=x2+AB2-AO2=x2+16,
解之可得:x=,
∴M为(,0);
如图,AM=AB,
则有|x+3|=5,
解之可得:x=2或x=-8,
∴M为(2,0)或(-8,0);
如图,BM=BA,
则BM2=BA2,
∴x2+16=25,
解之可得:x=3或x=-3(舍去),
∴M为(3,0);
∴满足条件的M为:(-8,0)或 (2,0)或 (3,0)或 (,0).
23.
(1)证明:∵四边形是菱形,,
∴ ,,
∴是等边三角形,
∴,,
∵
∴.
(2)①证明:连接,延长到点,使,连接.
由(1)知,
∴,
,,
∴,
∵是等边三角形,
∴,
∴,
∴,,
∴
∴是等边三角形,
∴.
②由①可知,
∵,∴,
又∵,
∴,
∴,
∴,即,
∴.
24.
解:(1)连接,如下图:
∵点D为BC边中点
∴
又∵为等腰直角三角形
∴,,
∴
又∵
∴
∴
∴
(2)分别过点、作、交于点
∵为等腰直角三角形
∴
又∵、
∴、为等腰直角三角形
∴,
∵,
∴
∴
∴
∴,,
∴,
∴
又∵
∴
∴,即
(3)∵,
∴
又∵
∴
∴
∴
设,
∴
∴当时,最大,最大为1.
一、单选题
1.若的面积是,则它的三条中位线围成的三角形的面积是( )
A. B. C. D.无法确定
2.如图,矩形中,,,点P在对角线上,且,连接并延长,交的延长线于点Q,连接,则的长为( )
A. B. C. D.
3.如图,ABC中,DE∥BC,AD:BD=1:3,则OE:OB=( )
A.1:3 B.1:4 C.1:5 D.1:6
4.如图,在矩形中,是的中点,若交于点,是的中点,连接,,则的长为( )
A. B. C.1 D.
5.如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为( )
A. B. C. D.
6.如图,在平行四边形ABCD中,点E是AD上一点,,连接BE交AC于点G,延长BE交CD的延长线于点F,则的值为( )
A. B. C. D.
7.如图,中,,是中线, 是上一点,作射线,交于点,若,则 ( )
A. B. C. D.
8.小明想借助网格在线段AB上找一点P,使AP∶PB=2∶3,下列作法中错误的是( )
A. B.
C. D.
9.如图,在△ABC中,AB=AC,点D是BC边的中点,点E是AB边的中点,过点E作EF∥AD交BC于点F,过点E作EG∥BC交AD于点G,设△ABC的面积为S,则四边形EFDG的面积为( )
A.S B.S C.S D.S
10.直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A. B. C. D.
二、填空题
11.在△ABC和△DEF中,∠A=∠D=105°,AC=4cm,AB=6cm,DE=3cm,则DF=_________时,△ABC与△DEF相似.
12.如图,已知矩形ABCD中,AB=6,AD=8将矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,如果AE=2AM,那么CN的长为______.
13.如图,四边形中,对角线交于点O,,,,,如果,那么的值是___________.
14.如图,在平面直角坐标系中,与轴交于点,已知点,,,是线段上一点,连接,若与相似,则的长为______.
15.如图,在矩形ABCD中,点E在边BC上,连结AE,将△ABE沿直线AE翻折得到△AFE,EF与AC相交于点M.若AB=8,BC=10,且BE=BC,则点F到直线AD的距离为____.
16.如图,矩形ABCD沿EF折叠,点A的对称点为点A',点B的对称点为点B',A'B'与AD相交于点G,若点F,B',D在同一条直线上,△A'EG的面积为4,△CDF的面积为36,则△GB'D的面积等于______.
17.如图,已知在矩形纸片中,将纸片折叠,使顶点与边的点重合.若折痕分别与交于点的外接圆与直线有唯一一个公共点,则折痕的为______.
18.如图,在△ABC中,∠C=90°,BC=1,AC=2,、、…都是正方形,且、、…在AC边上,、、…在AB边上.则线段的长用含n的代数式表示为______________.(n为正整数)
三、解答题
19.如图,在梯形ABCD中,AD//BC,∠ABC=90°,且AB是AD,BC的比例中项,
求证:BD⊥AC.
20.如图正方形网格中,每个小正方形的边长均为1,只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中画等腰△ABC,使得∠CAB=90°;
(2)在图②中画等腰△DEF,使△ABC∽△DEF,且相似比为:1.
21.如图,△ABC中,点D,E分别是BC,AB上的点,CE,AD交于点 F,BD=AD,BE=EC.
求证:△ABD∽△CBE;
若CD=CF,试求∠ABC的度数.
22.如图,已知点在轴的负半轴上,点在轴的正半轴上,,,点在线段上,从点出发以每秒5个单位长度的速度向点运动,设运动时间为秒,过点作轴于点.
(1) 当时,线段的长为________;
(2) 当时,求的值;
(3) 在轴上是否存在点,使为等腰三角形,若存在,直接写出点的坐标,若不存在,说明理由.
23.在菱形中,,点、分别是边、上两点,满足,与相交于点.
(1)如图1,连接.求证:;
(2)如图2,连接.
① 求证:;
② 若,,求线段的长(用含、的代数式表示).
24.如图1,在等腰中,,点D为斜边AB边上一动点(不含端点).作,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
【问题发现】
(1)如图1,若点D为BC边中点.请直接写出DE,DF的数量关系_________.
【类比探究】
(2)如图2,若点D为BC边上一动点,且.猜想DF与DE的数量关系.并证明你的结论.
【拓展应用】
(3)如图3,在边长为4的等边中,点D为BC边上一动点,作.DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.
答案
一、单选题
1.A
【分析】
根据三角形中位线定理即可证得:,则△DEF∽△ABC,根据相似三角形的面积的比等于相似比的平方即可求解.
解:如图:
∵DE是△ABC的中位线,
∴DE=BC,即,
同理,,,
∴,
∴△DEF∽△ABC,
∴,
∴S△DEF=S△ABC=×8=2(cm2).
故选:A.
2.C
【分析】
根据矩形的性质可求BD,,从而得到QC,由勾股定理即可求解;
解:∵在矩形中,,,
∴
∵AB∥CD,
∴
∵
∴
∵
∴
∴
∴
故选:C.
3.B
【分析】
先根据DE∥BC,得出ADE∽ABC,进而得出 ,再根据DE∥BC,得到ODE∽OCB,进而得到.
解:∵DE∥BC,
∴ADE∽ABC,
∴,
又∵,
∴,
∵DE∥BC,
∴ODE∽OCB,
∴.
故选:B.
4.C
【分析】
先证明,可得3EF=,延长AE交DC得延长线于点H,可得,继而即可求解.
解:∵在矩形中,
∴AD∥BC,AD=BC,
∴,
∴,即:3EF=,
延长AE交DC得延长线于点H,
∵AB∥CD,
∴∠ABE=∠HCE=90°,
∵是的中点,
∴BE=CE,
又∵∠AEB=∠CEH,
∴,
∴AE=EH,AB=CH=CD,即C是DH的中点,
∵是的中点,
∴HF=2,
∵3EF=,
∴4EF=4,
∴EF=1,
故选C.
5.B
【分析】
根据题意,画出示意图,易得△EDC∽△FDC,进而可得,即DC2=ED FD,代入数据可得答案.
解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又
∴△EDC∽△CDF,
∴,即DC2=ED FD=2×8=16,
解得CD=4m(负值舍去).
故选:B.
6.A
【分析】
先根据平行四边形的性质得到AB∥CD,则可判断△ABG∽△CFG,△ABE∽△DFE,于是根据相似三角形的性质和AE=2ED即可得结果.
解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△ABG∽△CFG,
∴=
∵△ABE∽△DFE,
∴=,
∵AE=2ED,
∴AB=2DF,
∴=,
∴=.
故选:A.
7.C
【分析】
作,交于点,则有,根据 ,,可得,,再根据是边上的中线,得到,;根据可得,则,化简即可得到结果.
解:如图,作,交于点,
∴
∴,
又∵,,
∴,
∴,
∴
∵是边上的中线,
∴
∴,
∴,
∵
∴
∴
∴,
则.
故选:C.
8.D
【分析】
利用平行可证得三角形相似,再利用相似三角形的对应边成比例,对各选项逐一判断.
解:A、根据图形,可知两个三角形相似,且相似比为2∶3,故AP∶PB=2∶3,故正确,故此选项不符合题意.
B、根据图形,可知两个三角形相似,且相似比为2∶3,故AP:PB=2∶3,故正确,故此选项不符合题意.
C、如图,
根据图形可知:∠CAD=90°,线段CD绕点O顺时针旋转90°与AB重合,则∠APC=旋转角=90°=∠CAD,∠ACD=∠DCA,
∴△ACD∽△DCA,
∴,
∵AC=,AD=2, CD=,
∴AP=,
∵S△BCD=,
∴BP=,故AP∶PB=2∶3,故正确,故此选项不符合题意.
D、可知两个三角形不相似,故AP:PB之比无法判断,故错误,故此选项符合题意.
故答案为:D.
9.B
【分析】
根据等腰三角形的性质可得AD⊥BC,BDBC,然后可得四边形EFDG是矩形,再根据三角形中位线定理可得EGBDBC,DG=AGAD,进而可以解决问题.
解:∵AB=AC,点D是BC边的中点,
∴AD⊥BC,BDBC,
∴∠ADB=90°,
∵EF∥AD,EG∥BC,
∴四边形EFDG是平行四边形,
又∠ADB=90°,
∴四边形EFDG是矩形,
∵点E是AB边的中点,
∴AE=BE,
∴AG=DG,
∴EG是△ABD的中位线,
∴EGBDBC,DG=AGAD,
∵△ABC的面积为S,
∴SBC AD,
∴四边形EFDG的面积=FD DGBCADS.
故选:B.
10.A
【分析】
分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,可得AF=4,先根据全等三角形的判定定理得出△BCE≌△CAF,故可得出CF及CE的长,在Rt△ACF中根据勾股定理求出AC的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD的长,在Rt△BCD中根据勾股定理即可求出BD的长.
解:分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,垂足为F、E、G,
∵l1与l2的距离为1,l2与l3的距离为3,
∴AF=4,BE=DG=3,
∵△ABC是等腰直角三角形,
∴AC=BC,
∵∠EBC+∠BCE=90°,∠BCE+∠FCA=90°,∠FCA+∠CAF=90°,
∴∠EBC=∠FCA,∠BCE=∠CAF,
在△BCE与△ACF中,,
∴△BCE≌△CAF,
∴CF=BE=3,
∴AC==5,
∵AF⊥l3,DG⊥l3,
∴△CDG∽△CAF,
∴,即,
解得:CD=,
∴BD==.
故选:A.
二、填空题
11.或
【分析】
由于两相似三角形的对应边不能确定,故应分△ABC∽△DEF与△ABC∽△DFE两种情况进行讨论.
解:∵∠A=∠D,AB=6cm,AC=4cm,DE=3cm,
∴当△ABC∽△DEF时,=,即,
解得:DF=2;
当△ABC∽△DFE时,=,
即,
解得:DF=4.5.
综上所述,当DF=2cm或4.5cm时,△ABC和△DEF相似.
故答案为:2cm或4.5cm.
12.
【分析】
如图,过N作NF⊥AD于F,可得NF=AB,根据矩形的性质和折叠的性质可得∠MEN=∠B=90°,EN=BN,根据直角三角形两锐角互余的性质及平角的定义可得∠AME=∠NEF,进而可证明△AEM∽△FNE,根据AE=2AM可求出EF的长,在Rt△FNE中,利用勾股定理可求出EN的长,进而可求出CN的长.
解:如图,过N作NF⊥AD于F,
∵四边形ABCD是矩形,AB=6,
∴NF=AB=6,
∵矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,
∴EN=BN,∠MEN=∠B=90°,
∴∠AEM+∠NEF=90°,
∵∠AEM+∠AME=90°,
∴∠AME=∠NEF,
又∵∠A=∠EFN=90°,
∴△AEM∽△FNE,
∴,
∵AE=2AM,NF=6,
∴EF=3,
∴BN=EN===,
∵BC=8,
∴CN=BC-BN=8-,
故答案为:8-
13.
【分析】
由题意可以证得△AOD∽△BOC,再根据相似三角形的性质得到AO:OD=BO:OC,从而得到△AOB∽△DOC,最后再根据相似三角形的性质得到解答.
解:在△AOD和△BOC中,,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴AO:OB=DO:OC=AD:BC=1:2,
∴OB=4,DO=3,
∴在△AOB和△DOC中,∠AOB=∠DOC,AO:OD=BO:OC=2:3,
∴△AOB∽△DOC,
∴= AO:OD=2:3,
故答案为.
14.2或4
【分析】
是一个直角三角形,若与相似,必须证明是直角三角形,再用相似三角形的性质即可求出点M的坐标.
解:如图,
∵A(1,4) , C(3,0) , D(0,3) ,
∴ ,,,
;
∴是直角三角形
∵点M在x轴上,设点M的坐标是(x,0),
∽
∴
∴=1
∴
当时,CM=2;当时CM=4,
故答案为:2或4.
15..
【分析】
先过F作MN⊥BC,根据已知条件与折叠的性质得到△AFN∽△FEM,再根据相似的性质得到,设出未知数,求解出答案即可.
解:过F作MN⊥BC,
∵BE=,BC=10,
∴BE=6,
∵翻折
∴△ABE≌△AFE,
∴EF=BE=6,∠AFE=∠B=90°,AF= AB=8,
∴∠AFN+∠EFM=90°,
∵∠AFN+∠FAN=90°,
∴∠FAN=∠EFM,
∴△AFN∽△FEM,
∴,
设AN=4x,FM=3x, FN=8-3x,EM=4x-6,
∴FN=8-3x,EM=4x-6,
∴,
∴,
经检验:是原方程的根,
∴,
故答案为:.
16.16
【分析】
由矩形ABCD沿EF折叠, 可得∠A′=∠A =90°,A′B′=AB,可证A′E∥DF,可得∠A′EG=∠GDB′,可证△A′EG∽△CFD,可得,可证△A′EG∽△B′DG,即可.
解:∵矩形ABCD沿EF折叠,点A的对称点为点A',点B的对称点为点B',
∴∠A′=∠A=∠A′B′F=∠B=∠C=90°,A′B′=AB,
∵∠A′+∠A′B′F=180°,
∴A′E∥DF,
∴∠A′EG=∠GDB′,
∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,
∴∠GDB′=∠DFC=∠A′EG,
∴△A′EG∽△CFD,
∴,
∴即,
∴,
∵∠A′=∠A′B′F=90°,∠A′EG=∠GDB′,
∴△A′EG∽△B′DG,
,
∵S△A'EG=4,
∴.
故答案为:16.
17.
【分析】
根据折叠的性质判断出AG=GE,∠AGF=∠EGF,再由CD∥AB得出∠EFG=∠AGF,从而判断出EF=AG,得出四边形AGEF是平行四边形,继而结合AG=GE,判定四边形AGEF是菱形;连接ON,得出ON是梯形ABCE的中位线,在RT△ADE中,利用勾股定理可解出x,继而可得出折痕FG的长度.
解:由折叠的性质可得,GA=GE,∠AGF=∠EGF,
∵DC∥AB,
∴∠EFG=∠AGF,
∴∠EFG=∠EGF,
∴EF=EG=AG,
∴四边形AGEF是平行四边形(EF∥AG,EF=AG),
又∵AG=GE,
∴四边形AGEF是菱形
令△AED的外接圆与直线有唯一一个公共点为N,连接ON,如图所示,
∵△AED是直角三角形,AE是斜边,点O是AE的中点,△AED的外接圆与BC相切于点N,
∴ON⊥BC,
∵点O是AE的中点,
∴ON是梯形ABCE的中位线,
设CE=x,则ED=2-x,2ON=CE+AB=x+2,
在Rt△AED中,AE=2OE=2ON=x+2,
AD2+DE2=AE2,
∴12+(2-x)2=(2+x)2,
得x=,
,
∵△FEO∽△AED,
∴,
解得:FO=,
∴FG=2FO=.
故答案为:.
18.
【分析】
根据题意得出△BB1C1∽△BAC,进而求出B1C1=,同理可得出:B2C2=,B3C3=,…,进而得出答案.
解:由题意可得:B1C1//AC,
∴△BB1C1∽△BAC,
∴BC1:BC=B1C1:AC,
∵CC1=B1C1,
∴B1C1:2=(1 C1B1):1,
解得:B1C1=,
故A1B1=,AA1=,
同理可得出:B2C2=,B3C3=,…,
∴线段BnCn的长用含n的代数式表示为:.
故答案为:.
三、解答题
19.
解:∵AD∥BC,∠ABC=90°,
∴∠BAD=90°,
∵AB是AD,BC的比例中项,
即AB2=AD BC,
∴
而∠ABC=∠DAB,
∴△ABC∽△DAB,
∴∠ABD=∠ACB,
∵∠ABD+∠DBC=90°,
∴∠ACB+∠DBC=90°,
∴∠BEC=90°,
∴BD⊥AC.
20.
解:(1)如图①中,△ABC即为所求;
,,,
,
,
的等腰直角三角形,
(2)如图②中,△DEF即为所求.
,,,
,
.
△ABC∽△DEF,且相似比为:1.
21.
(1)证明:∵BD=AD,BE=EC
∴∠B=∠BAD,∠B=∠BCE
∴∠BAD=∠BCE
而∠B=∠B,
∴△ABD∽△CBE
(2)解:设∠B=,由(1)可知∠B=∠BAD=∠BCE=,
∴∠ADC=
又∵CD=CF
∴∠ADC=∠DFC=
∴
∴
即
22.
(1)解:由题意可得:当时,PA=PB,且PQ∥AO,
∴,BQ=QO,
∴PQ为三角形ABO的中位线,
∴PQ=AO=,
故答案为;
(2)解:由题可知,PA=PQ=5t, ∴ PB=AB-PA=5-5t
∵PQ∥AO ∴∠BPQ=∠BAO
又∵BQP=∠BOA=90°
∴△BPQ∽△BAO
∴ 解得:t=
(3)解:由题意可设满足条件的M为(x,0),则可分三种情况:
如图,MA=MB,
则MA2=MB2,
∴(x+3)2=OM2+OB2=x2+AB2-AO2=x2+16,
解之可得:x=,
∴M为(,0);
如图,AM=AB,
则有|x+3|=5,
解之可得:x=2或x=-8,
∴M为(2,0)或(-8,0);
如图,BM=BA,
则BM2=BA2,
∴x2+16=25,
解之可得:x=3或x=-3(舍去),
∴M为(3,0);
∴满足条件的M为:(-8,0)或 (2,0)或 (3,0)或 (,0).
23.
(1)证明:∵四边形是菱形,,
∴ ,,
∴是等边三角形,
∴,,
∵
∴.
(2)①证明:连接,延长到点,使,连接.
由(1)知,
∴,
,,
∴,
∵是等边三角形,
∴,
∴,
∴,,
∴
∴是等边三角形,
∴.
②由①可知,
∵,∴,
又∵,
∴,
∴,
∴,即,
∴.
24.
解:(1)连接,如下图:
∵点D为BC边中点
∴
又∵为等腰直角三角形
∴,,
∴
又∵
∴
∴
∴
(2)分别过点、作、交于点
∵为等腰直角三角形
∴
又∵、
∴、为等腰直角三角形
∴,
∵,
∴
∴
∴
∴,,
∴,
∴
又∵
∴
∴,即
(3)∵,
∴
又∵
∴
∴
∴
设,
∴
∴当时,最大,最大为1.
同课章节目录
