5.1多边形（2）

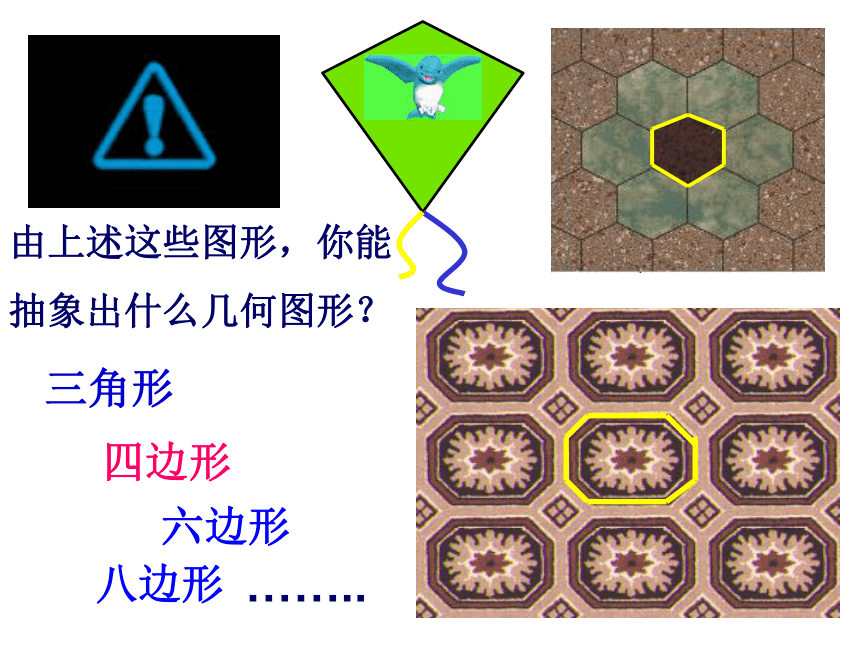
课件22张PPT。多边形(二)由上述这些图形，你能
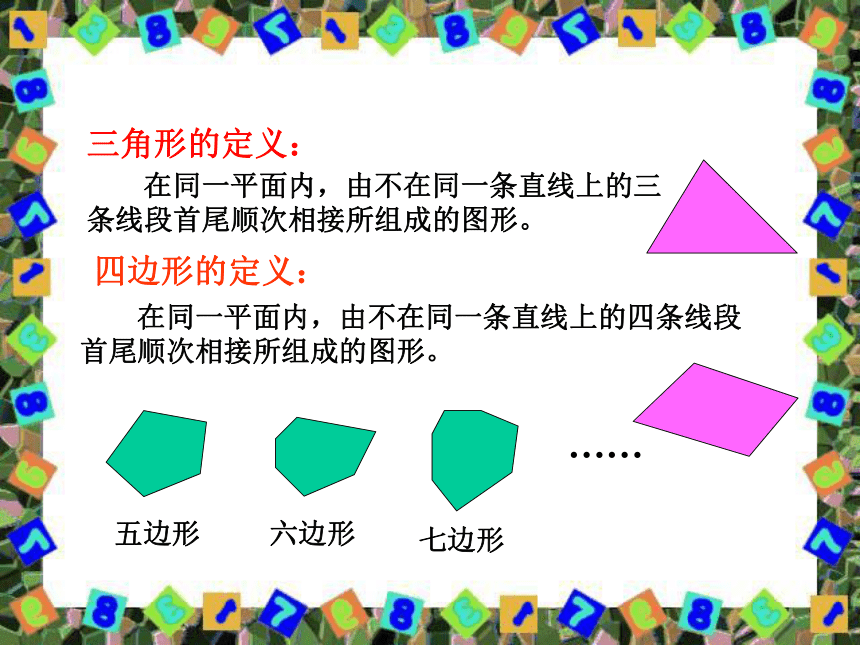
抽象出什么几何图形？三角形 四边形 六边形 八边形……..三角形的定义：　　在同一平面内，由不在同一条直线上的三条线段首尾顺次相接所组成的图形。四边形的定义：　　在同一平面内，由不在同一条直线上的四条线段首尾顺次相接所组成的图形。……五边形六边形七边形多边形的定义：　　在同一平面内，由不在同一条直线上的一些线段首尾顺次相接所组成的（封闭）图形。
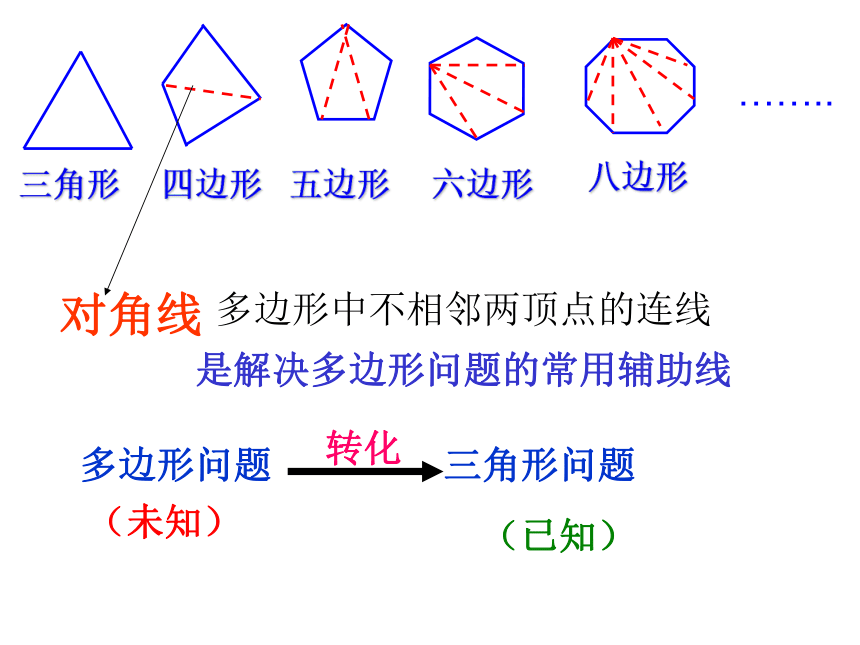
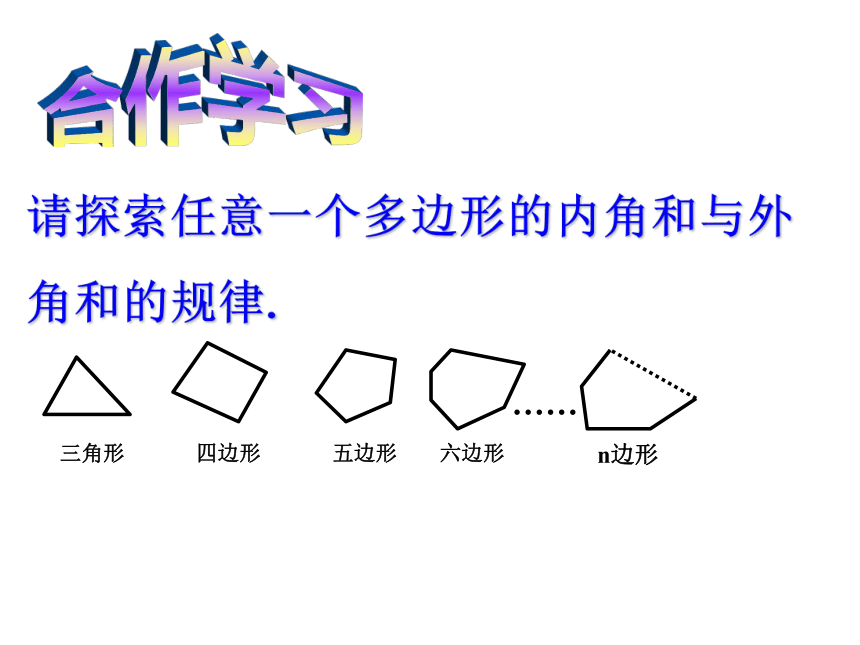
下定义　　多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。　　如果一个多边形由n条线段组成，那么这个多边形就叫做n边形。三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化（未知）（已知）多边形中不相邻两顶点的连线合作学习请探索任意一个多边形的内角和与外角和的规律.23n-3
34n-23×1800
4×1800
122×1800
1800
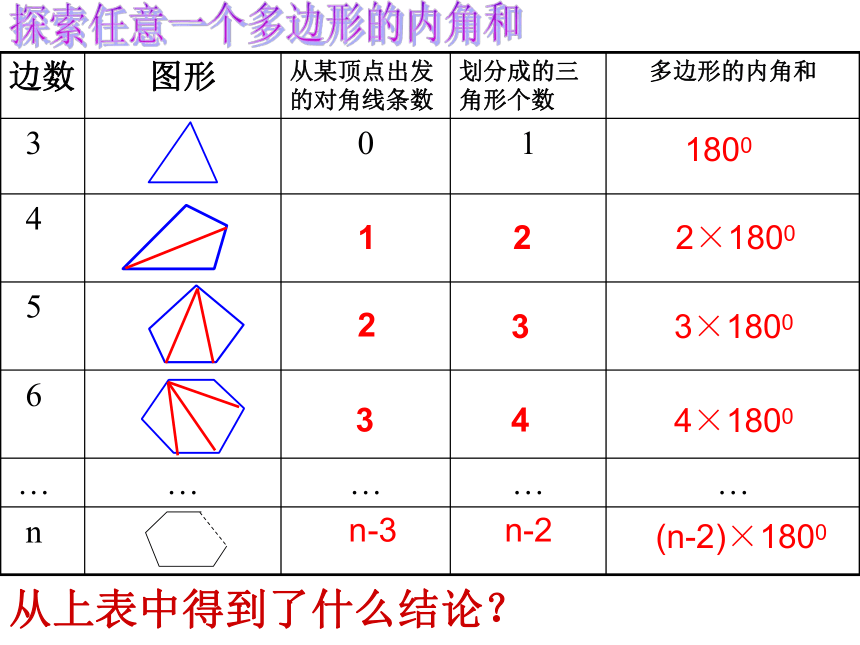
探索任意一个多边形的内角和从上表中得到了什么结论？(n-2)×1800
从上表中得到了什么结论？结论：n边形的内角和为：
（n－2）×180°(n≥3).n边形共有对角线 条(n≥3)n边形从一个顶点出发的对角线有 条(n≥3)(n－3)
１、一个十边形的内角和是 　　 度。 ２、如果一个多边形的内角和是900度，那么 这是 　 边形。 　　　　 　　　　　　　　
1440七抢答3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和结论：任何多边形的外角和为360° 抢答 过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.我会我成功！（2）已知一个多边形的内角和为720o ，则这个多边形是______边形6（1）八边形的内角和为______，外角和为_____1080360o（3）已知一个多边形的每一个外角都是72o，求这个边形的边数为______5（4）在五边形ABCDE中，若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o（5） 一个内角和为1620°的多边形可连 条对角线。44王大意在计算某多边形的内角和时，得到的答案是2070°，老师发现他把其中一个外角也加了进去。你知道王大意计算的是几边形的内角和吗？那个加进去的外角是多少度？挑战自我(2008湖南株洲)如下图中每个阴影部分是以多边形各顶点为圆心，1为半径的扇形，并且所有多边形的每条边长都大于2，则第个多边形中，所有扇形面积之和是 （结果保留π）.

……
第1个 第2个 第3个点击中考∵AB∥DE， CD∥AF（已知）∴∠1＝∠3，∠2＝∠4（两 直线平行，内错角相等） ∴∠1+∠2＝∠3+∠4，
即∠FAB＝∠CDE，同理∠B＝∠E，∠C＝∠F∴∠FAB＋∠C＋∠E= 1／2 ×720°=360°∵∠FAB+∠ABC+∠BCD+∠CDE＋∠DEF＋∠AFE=（6-2）×180°=720°解：∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1＝∠2，∴∠CDE=∠FAB同理∠AFE＝∠BCD，∠ABC=∠DEF∴∠FAB＋∠BCD＋∠DEF= ×720°=360°例： 一个六边形如图，已知AB∥DE，BC∥EF， CD∥AF，求∠A＋∠C＋∠E的度数。 拓展一：一个六边形如图，已知 BA∥DE ，∠B= ∠ E，∠C=∠F
（1）求证：CD∥AF
（2）求∠A＋∠C＋∠E的度数．已知
;
;拓展二：六边形ABCDEF的
每个内角度数是120度,且AF=AB=3,BC=CD=2.
求：DE，EF的长度．这节课你学到了什么?
还有什么困惑？. 一个定义
一组公式

一个性质
一种重要数学思想方法（转化思想）
一种常见辅助线
谈一谈五个一谢谢指导SEE YOU ！