第六章反比例函数 复习课件

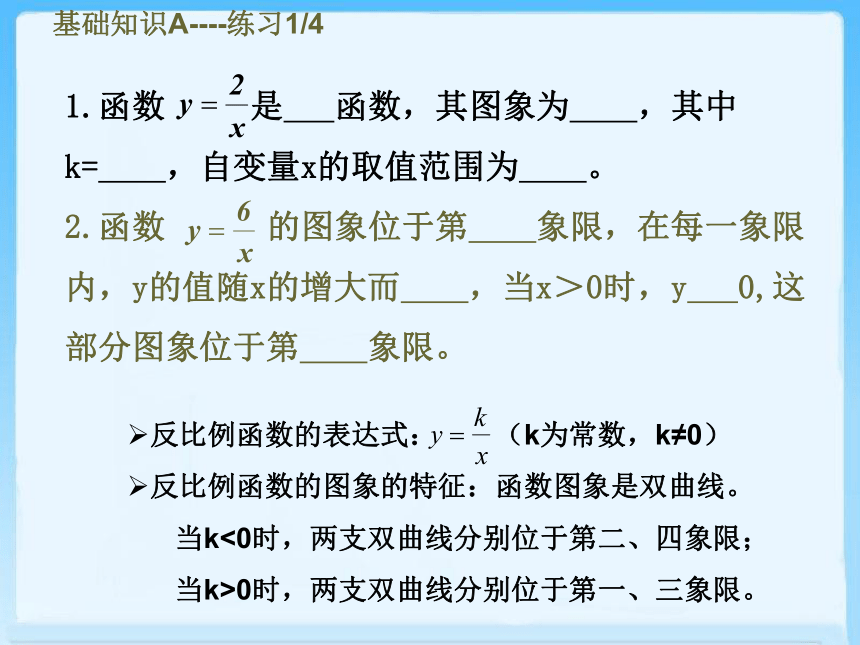
课件18张PPT。第6章 反比例函数习题课1.函数 是 函数，其图象为 ，其中k= ，自变量x的取值范围为 。
2.函数 的图象位于第 象限，在每一象限内，y的值随x的增大而 ，当x＞0时，y 0,这部分图象位于第 象限。基础知识A----练习1/43．下列函数关系式中，不是反比例函数的是（　　）
A、　　　 B、　　 C、y=3x　　 D、
4．若反比例函数 的图象在第二、四象限内，则k的取值范围是　（　　）
A、k>1 　 　　B、k≤1 　C、k≥1 D、k<1
5.已知△ABC的面积为12，则△ABC的高h与它的底边a的函数关系式为 .基础知识A----练习2/4
6.下列函数中,图象位于第二、四象限的有 ；在图象所在象限内，y的值随x的增大而增大的有 .基础知识A----练习3/4反比例函数的性质是：
当k>0时，在每一个象限内，y随x的值的增大而减小；
当k<0时，在每一个象限内，y随x的值的增大而增大。7.已知点A(-2,y1)，B(-1,y2)都在反比例函数 的图象上,则y1与y2的大小关系为 。8.已知点A(-2,y1)，B(-1,y2)都在反比例函数 (k＜0)
的图象上,则y1与y2的大小关系为 。9.已知点A(-2，y1)、B(-1，y2)、C(4，y3)都在反比例函数
(k＜0)的图象上，则y1、y2与y3的大小关系为 。基础知识A----练习4/4
基础知识A10.关于反比例函数 ：
⑴ 当x＜0时，y的取值范围是 ；
⑵ 当y＞10时，x的取值范围是 。11.关于反比例函数 ：
⑴ 当1＜x＜8时，y的取值范围是 ；
⑵ 当y＜4时，x的取值范围是 。基础知识B---取值范围12. 函数 y=kx+k 与 同一条直角坐标系中的图象可能是 ( )基础知识C---图像位置在每一个象限内:
当k>0时，y随x的增大而减小;
当k<0时，y随x的增大而增大.y=kx(k≠0)( 特殊的一次函数)当k>0时，y随x的增大而增大;
当k<0时，y随x的增大而减小.正比例函数与反比例函数13.如图，点P是反比例函数 图象
上的一点，PD⊥x轴于D，则△POD的
面积为 。14.如图，点P是反比例函数图象上的一
点，过点P分别向x轴、y轴作垂线，
若阴影部分面积为3,则这个反比例
函数的关系式是 。基础知识D---图像的特殊性15.如图，点P是x轴正半轴上的一个动点，过点P作x轴的垂线PQ交双曲线于点Q，连接OQ，当点P沿x轴的正方向运动时，Rt△OPQ的面积 （ ）
A、逐渐增大　 B、逐渐减小　
C、保持不变　　 D、无法确定
16.如果反比例函数 与正比例函数 y=kx 的一个交点为（-3，m），则另一个交点的坐标为 。基础知识D---图像的特殊性反比例函数的图象是中心对称图形，
也是轴对称图形。

设A是反比例函数 （k≠0）图象上的任意一点，过A点分别作x轴，y轴的垂线AM，AN,则所得矩形NOMA的面积为︱k︱。三角形AOM的面积为 。
基础知识D---图像的特殊性17.老师给出一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质:
甲:函数的图象经过第二象限;
乙:函数的图象经过第四象限;
丙:在每个象限内,y随x的增大而增大.
请你根据他们的叙述构造满足上述性质的一个函数: .综合应用1/2综合应用2/218.已知点A（3，4），B（－2，m）在反比例函数
的图象上，经过点A、B的一次函数的图象分别与x轴、y轴交于点C、D。
⑴ 求反比例函数的解析式；⑵ 求经过点A、B的一次函数的解析式；⑶ 求S△ABO；综合应用2/218.已知点A（3，4），B（－2，m）在反比例函数
的图象上，经过点A、B的一次函数的图象分别与x轴、y轴交于点C、D。
⑴ 求反比例函数的解析式；⑵ 求经过点A、B的一次函数的解析式；⑷ 当x为何值时反比例函数y的值
大于一次函数y 的值综合应用2/218.已知点A（3，4），B（－2，m）在反比例函数
的图象上，经过点A、B的一次函数的图象分别与x轴、y轴交于点C、D。
⑴ 求反比例函数的解析式；⑵ 求经过点A、B的一次函数的解析式；⑸ 在y轴上找一点P，使PA＋PC最短，
求点P的坐标；综合应用2/218.已知点A（3，4），B（－2，m）在反比例函数
的图象上，经过点A、B的一次函数的图象分别与x轴、y轴交于点C、D。
⑴ 求反比例函数的解析式；⑵ 求经过点A、B的一次函数的解析式；⑹ 在y轴上找一点H，使△AHO为等腰三角形，求点H的坐标;综合应用2/218.已知点A（3，4），B（－2，m）在反比例函数
的图象上，经过点A、B的一次函数的图象分别与x轴、y轴交于点C、D。
⑴ 求反比例函数的解析式；⑵ 求经过点A、B的一次函数的解析式；⑺ 若E是线段DA上的一动点，如图，EM平行y轴，且交反比例函数图像于点M，ER⊥y轴于点R，MQ⊥y轴于点Q，那么四边形ERQM面积是否可以取得最大值或最小值？为什么？