第四章 相似三角形 复习课件

课件55张PPT。第四章 相似三角形复习课第一课时一.比例线段知识要点11. 成比例的数（线段）：其中 ：a、b、c、d 叫做组成比例的项，a、d 叫做比例外项，b、c 叫做比例内项，比例的性质：1.若a, b, c, d成比例,且a=2, b=3, c=4,那么d= 62、下列各组线段的长度成比例的是（ ）A. 2 , 3, 4, 1 B. 1.5 ,2.5 ,6.5 , 4.5 C. 1.1 ,2.2 ,3.3 ,4.4 D. 1 , 2 , 2 , 4 练习:D 653、4、已知 1) x：(x+2)=(2—x)：3，求x。
(2)若 ， 求 。
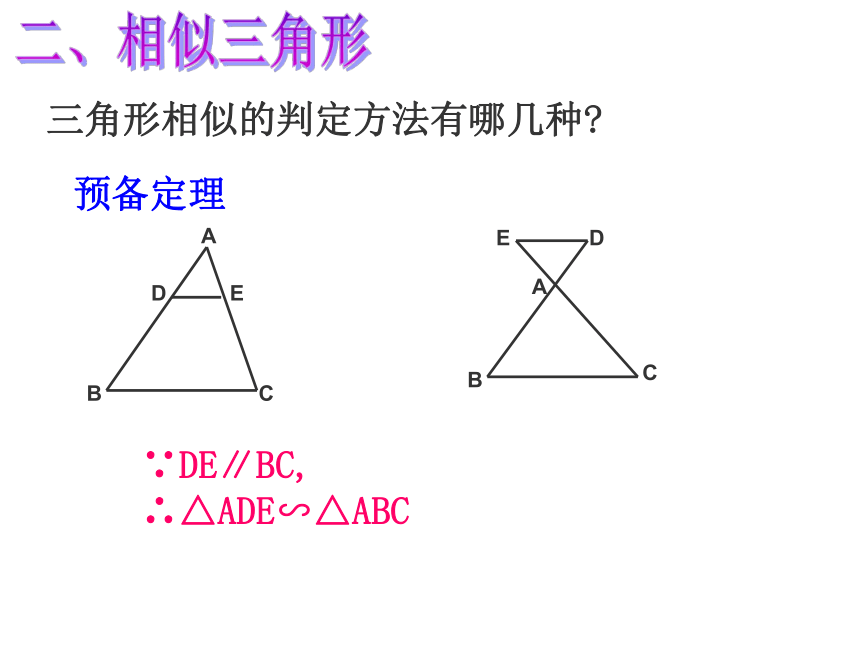
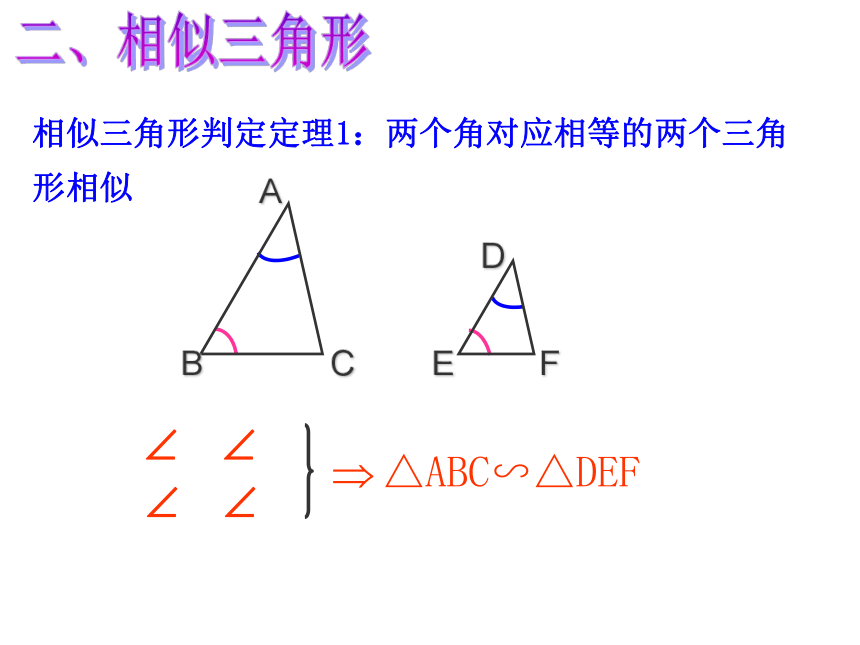
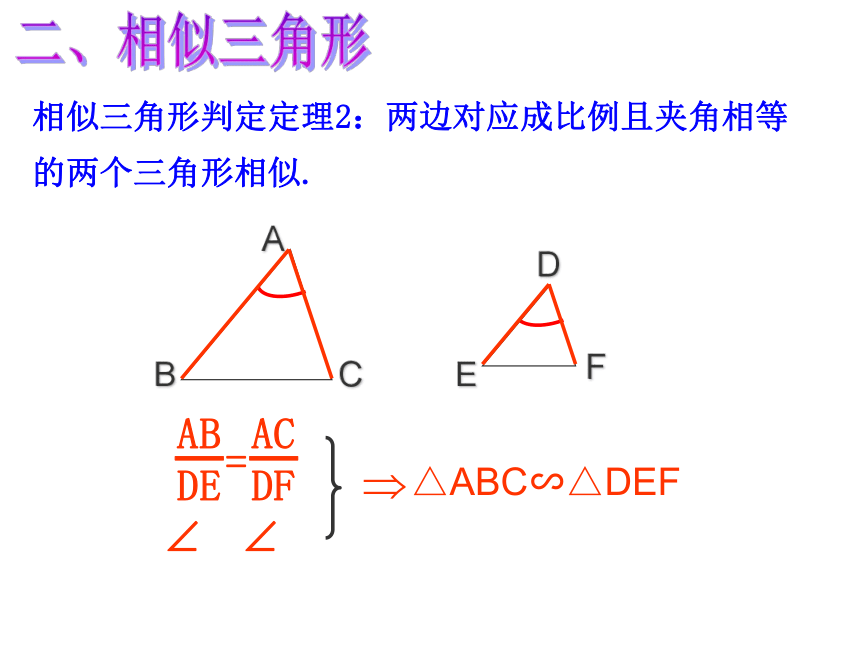
(3) 若 ， 求 ，1或-47/31/5,-4/556 已知1, 2, 3三个数，请你再添上一个数，写出一个比例式。6或2/3或1.5一.比例线段2.比例中项：练习：当两个比例内项相等时，那么线段 b 叫做a 和 c 的比例中项.一.比例线段3.黄金分割：练习：定义：对应角相等、对应边成比例的三角形叫做相似三角形。相似比：相似三角形的对应边的比，叫做相似三角形的相似比。二、相似三角形知识要点2三角形相似的判定方法有哪几种?预备定理∵DE∥BC, ∴△ADE∽△ABC二、相似三角形相似三角形判定定理1：两个角对应相等的两个三角形相似二、相似三角形相似三角形判定定理2：两边对应成比例且夹角相等的两个三角形相似.二、相似三角形相似三角形判定定理3：三边对应成比例的两个三角形相似.△ABC∽△DEF二、相似三角形相似三角形的判定：（1）平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似；
（2）有两个角对应相等的两个三角形相似；
（3）两边对应成比例,且夹角相等的两个三角形相似；
（4）三边对应成比例的两个三角形相似.二、相似三角形ADEBACBABCD△ADE绕点A旋转DCADEBCABCDEBCADE点E移到与C点重合∠ACB=Rt∠CD⊥AB相似三角形基本图形的回顾：相似三角形的性质：1、相似三角形的对应角相等，对应边成比例2、相似三角形的周长比等于相似比，对应高的比
等于相似比3、相似三角形的面积比等于相似比的平方二、相似三角形二.知识应用:1.找一找:(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.(2) 如图2,已知:△ABC中, ∠ACB=Rt∠ ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.344(4)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,则图中共有_____对三角形相似.(5)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,且AC平分∠BAD,则图中共有_____对三角形相似.626.将两块完全相同的等腰直角三角形摆放成如图所示的样子,假设图形中的所有点,线都在同一平面内,试写出一对相似三角形(不全等)______________.△ADE、△BAE、△CDA都相似1.如图，正方形ABCD的边长为8，E是AB的中点，点M，N分别在BC，CD上，且CM=2，则当CN=_________时，△CMN与△ADE相似。1或4练一练:2.在平面直角坐标系，B（1，0）, A（3，－3）, C（3，0）,点P在y轴的正半轴上运动，若以O，B，P为顶点的三角形与△ABC相似，则点P的坐标是__________________.·P（0，1.5）或（0，2/3）练一练3、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________练一练4、 如图, 在直角梯形中, ∠BAD=∠D=∠ACB=90。，
CD= 4, AB= 9, 则 AC=______6 5、如图, 已知点P是边长为4的正方形ABCD内的一点，且PB=3，BF⊥BP. 试问在射线BF上是否存在一点E，使以点B、E、C为顶点的三角形与△ABP相似?若存在,请求出BE的长;若不存在,请说明理由.FＥＥ练一练练一练6、在?ABC中，AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动，点Q从点B开始沿BC向点C以4cm/秒的速度移动，如果P、Q分别从A、B同时出发，经几秒钟?BPQ与?BAC相似？或AP:AC=AC:AB练一练7、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?8、如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足怎样关系时, △PCA∽△BDP.
(2)当△PCA∽ △BDP时,求∠APB的度数.练一练9、 如图D,E分别AB,AC是上的点, ∠AED=72o，
∠A=58o，∠B=50o, 那么△ADE和△ABC相似吗？若AE=2,AC=4,则BC是DE的 倍.练一练10、若△ ACP∽△ABC，AP=4，BP=5，则AC=_______，△ ACP与△ABC的相似比是_______，周长之比是_______，面积之比是_______。62 : 32 : 3练一练4 : 911、如图：已知∠ABC＝∠CDB＝90°，AC＝5cm，BC=3cm，当BD取多少cm时 △ABC和△BDC相似？4(2)以正方形的边长等量过渡.（3）请找出图中的相似三角形练一练13、在平行四边形ABCD中,AE:BE=1:2.若S△AEF=6cm2,则S△CDF = cm254S △ADF=____cm218练一练
14、如图（６）， △ＡＢＣ中，ＤＥ??ＦＧ??ＢＣ，ＡＤ＝ＤＦ＝ＦＢ，则Ｓ△ＡＤＥ:Ｓ四边形ＤＦＧＥ:Ｓ四边形ＦＢＣＧ=_________
答案：１：３：５画一画:1、如图,在△ABC和△DEF中, ∠A=∠D=700, ∠B=500, ∠E=300,画直线a,把△ABC分成两个三角形,画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)300300200200画一画 2、 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)(2)在右图中,请你再画一个格点三角形,使它与△ABC相似(相似比不为1),但与图1中所画的三角形大小不一样.例1、如图,正方形ABCD中,E是DC中点,FC= BC.
求证: AE⊥EF证明:∵四边形ABCD是正方形∴BC=CD=AD，∠D=∠C=90°∵E是BC中点，FC= BC∴∴∴△ADE∽△ECF∴∠1=∠2∵∠D=90°∴∠1+ ∠3=90 °∴∠2+ ∠3=90°∴ AE⊥EF例2、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解：∵DE∥BC，EF∥AB∴∠A=∠CEF，∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴例3、如图,⊙O是△ABC的外接圆,AB=AC.
求证:AB2=AE·AD证明：连接BD∵AB=AC∴∠ADB=∠ABE又∵∠BAD=∠EAB∴△ABC∽△AEB∴∴AB2=AE·AD 证明：∵CD⊥AB， E为AC的中点
∴ DE=AE
∴∠EDA=∠A
∵ ∠EDA=∠FDB
∴∠A=∠FDB
∵∠ACB= Rt ∠
∴ ∠A=∠FCD=900-∠CBA
∴ ∠FDB=∠FCD
∵ ∠F= ∠F
∴ △FDB∽△FCD
∴ BD：CD=DF：CF
∴ BD·CF=CD·DF

例4 如图，CD是Rt△ABC斜边上的高，E为AC的中点，
ED交CB的延长线于F。CEADFB求证：BD·CF=CD·DF例5. 过ABCD的一个顶点A作一直线分别交对角线BD、边 BC、边DC的延长线于E、F、G .
求证：EA2 = EF· EG . 分析：要证明
EA2 = EF· EG ，
即 证明 成
立，而EA、EG、EF三条线段在同一直线上，无法构成两个三角形，此时应采用换线段、换比例的方法。可证明：△AED∽△FEB， △AEB ∽ △GED.证明：∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴例6、如图, 在△ABC中,∠ACB= 900，四边形BEDC为正方形, AE交BC于F, FG∥AC交AB于G. 求证: FC=FG. 证明: ∵四边形BEDC为正方形∴CF∥DE ∴△ACF∽△ADE∴ ①又∵FG ∥AC∥BE∴△AGF∽△ABE∴ ②由①②可得：又∵ DE=BE∴FC=FG例7、如图, AB/AD=BC/DE=AC/AE.
(1) 求证: ∠BAD= ∠CAE;
(2) 若已知 AB=6, BD=3, AC=4, 求 CE 的长.(1) ∵ 得∴ΔABC∽ΔADE ∴ ∠BAC=∠DAE∴ ∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE(2) 由∴∵∠BAD=∠CAE ∴ΔABD∽ΔACE∴∴ 证明：相似三角形性质应用2. 如图, AD⊥BC, D为垂足, AD=8, BC=10, EFGH是△ABC内接矩形,(H、G是BC上的两个动点,但H不到达点B, G不到达点C) 设 EH=x,EF=y
(1)求y与x之间的函数关系式,并求自变量x的取值范围;
(2)当EF+EH=9时,求矩形EFGH的周长和面积.相似三角形性质应用相似三角形性质应用 4、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（1）求证：△ABD∽△DCE（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值（3）当△ADE是等腰三角形时，求AE的长拓展提高1 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（1）求证：△ABD∽△DCE∵∠ADC是△ABD的外角∴∠ADC=∠ADE+∠2=∠B+∠1）21证明：∵AB=AC，∠BAC=90°∴∠B=∠C=45°又∵∠ADE=45°∴∠ADE=∠B∴∠1=∠2∴ △ABD∽△DCE（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值解：∵△ABD∽△DCE1∴∴∴ 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（3）当△ADE是等腰三角形时，求AE的长AD=AEAE=DEDE=AD 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°1分类讨论5、如图,在直角梯形ABCD中,AB∥CD, ∠A=900,AB=2, AD=5,P是AD上一动点(不与A、D重合),ＰＥ⊥ＢＰ，ＰＥ交ＤＣ于点Ｅ．（１）△ABP与△DPE是否相似？请说明理由；（２）设ＡＰ＝x　ＤＥ=y，求y与x之间的函数关系式,并指出自变量x的取值范围；（3）请你探索在点P运动的过程中，四边形ABED能否构成矩形？如果能，求出AP的长；如果不能，请说明理由；（4）请你探索在点P运动的过程中，△BPE能否成为等腰三角形？如果能，求出AP的长，如果不能，请说明理由。25xy5-x拓展提高6.如图，梯形ABCD中 AD∥BC ，∠ABC=90°，AD=9，BC=12，AB=10，在线段BC上任取一P，作射线PE⊥PD，与线段AB交于点E.（1）试确定CP=5时点E的位置；（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式，并求出自变量x的取值范围.提示：体会这个图形的“模型”作用，将会助你快速解题！拓展提高
7.如图，已知抛物线与x轴交于A、B
两点，与y轴交于C点.
（1）求此抛物线的解析式；
（2）抛物线上有一点P，满足
∠PBC=90°，求点P的坐标；
（3）在（2）的条件下，问在y轴
上是否存在点E，使得以A、O、E
为顶点的三角形与⊿PBC相似？若
存在，求出点E的坐标；若不存在，
请说明理由.23Q6拓展提高8、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10m，20m的梯形空地上种植花木（如下图）
（1）他们在△AMD和△BMC地带种植太阳花，单价为8元/m2。当在△AMD地带 （图中阴影部分）中种满花后，共用去了160元。请计算种满△BMC地带所需的费用 是多少元。
（2）若其余地带要种的有玫瑰花和茉莉花两种花木可供选择，单价分别为12元/m2、10元/m2，应选择哪种花木，刚好用完所筹集的资金？
（3）若梯形ABCD为等腰梯形，面积不变（如图2），请你设计一种花坛图案，即在梯形内找到一点P，使得△APB≌ △DPC，且△APD的面积与△BPC的面积相等，并说明你的理由。拓展提高作业如图，在平面直角坐标系中，A（0，1）、B（3，0）、C（-1，0）D（-2，0），连结AB、AC、AD.
(1) AD的长为___________；
(2) 找出图中相似的一对三角形，并说明
相似的理由；
(3) ∠ABD+∠ADB=_________度.必做题：选做题：2. 如图，平面直角坐标系中，直线AB与x轴y轴分别A（3，0）B（0， ）两点，点C为线段AB上的一动点，过点C作CD⊥x轴于点D.
(1)求直线AB的解析式；
(2)在第一象限内求作一点P,使得以P，O，B为顶点的三角形与⊿OBA相似,并求出所有符合条件的点P.