2023-2024学年浙教版八年级数学下册第3章数据分析初步 单元测试(含解析)
文档属性
| 名称 | 2023-2024学年浙教版八年级数学下册第3章数据分析初步 单元测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 605.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 00:00:00 | ||
图片预览



文档简介
第3章 数据分析初步(单元测试)
一、单选题(本大题共10小题,每小题3分,共30分)
1.在一竞赛中,老师将90分规定为标准成绩,记作0分,高出此分记为正,不足此分记为负,五名参赛者的成绩:,,,,0.那么( )
A.最高成绩为90分 B.最低成绩为88分
C.平均分为90分 D.平均分为分
2.坚定不移听党话,跟党走,让红色基因、革命薪火代代传承,某校组织开展“从小学党史,永远跟党走”系列的知识竞赛,培育孩子们的爱党、爱国情怀.下表是该学校学习小组知识竞赛的成绩统计表:
成绩 86 90 98 100
人数 1 3 1
已知该学习小组本次知识竞赛的平均分是分,那么表中的x的值是( )
A.4 B.5 C.6 D.7
3.在三个数字0,1,5中,再加入一个大于0的数字,使这四个数字的中位数为2,则加入的数字x是( )
A.1 B.2 C.3 D.4
4.小明前3次购买的西瓜单价如图所示,若第4次买的西瓜单价是元/千克,且这4个单价的中位数与众数相同,则a 的值为( )
A.5 B.4 C.3 D.2
5.习近平总书记指出:“扶贫先扶志,扶贫必扶智”,某企业扶贫小组准备为贫困户送温暖活动,该企业对扶贫对象的年龄结构进行了随机抽样调查,调查所得的一组数据的方差公式是,则这组数据的平均数和样本容量分别是( )
A.50,45 B.50,28 C.45,50 D.45,36
6.体育委员小聪要帮体育老师分析本班的跳远成绩,将各统计量计算好后却发现由于场地布置失误,导致每位同学的成绩都少记录了,则实际成绩与记录成绩相比( )
A.众数改变,方差改变 B.众数不变,平均数改变
C.中位数改变,方差不变 D.中位数不变,平均数不变
7.2023年两会期间,某校组织开展了以“聚焦两会”为主题的阅读活动,如图所示的扇形统计图描述了该校学生一周内阅读关于两会文章的篇数情况,则下列说法正确的是( )
A.该校学生阅读文章篇数的平均数为
B.阅读文章篇数为12的学生数量对应的扇形圆心角为
C.该校学生阅读文章篇数的众数为18
D.该校有一半以上的学生阅读文章的篇数大于15
8.下图是在2023年12月28日预报的我区2024年1月24日到31日八天的最低气温()统计图,这八天最低气温的众数和中位数为( )
A.3,2.5 B.3,3 C.,2 D.3,2
9.“雷达图”是一种常用统计图,它可以直观展示一个研究对象的不同方面.图是某学生某次测验的五门学科成绩的“雷达图”,如果从学科一到学科五计算平均成绩,则该学生这五门学科的平均成绩是( )
A.80 B.82 C.84 D.86
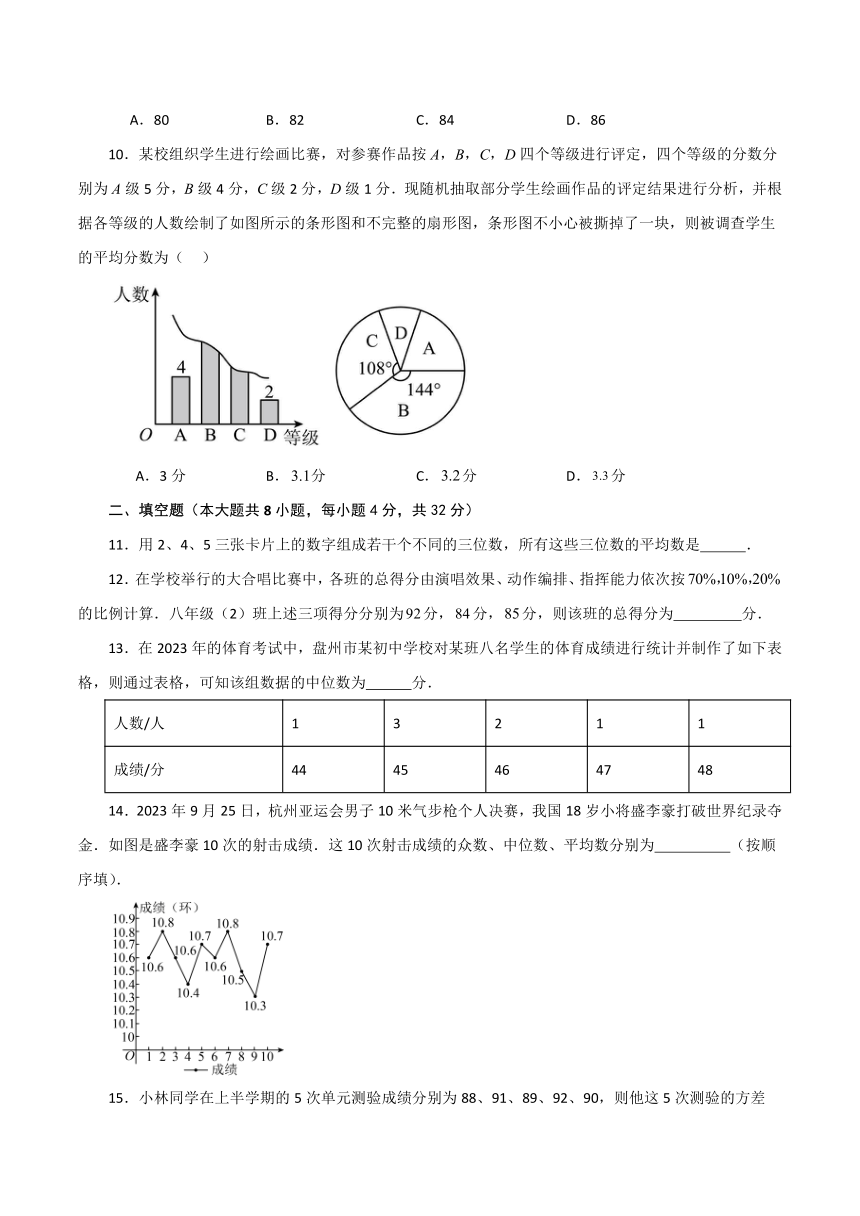
10.某校组织学生进行绘画比赛,对参赛作品按A,B,C,D四个等级进行评定,四个等级的分数分别为A级5分,B级4分,C级2分,D级1分.现随机抽取部分学生绘画作品的评定结果进行分析,并根据各等级的人数绘制了如图所示的条形图和不完整的扇形图,条形图不小心被撕掉了一块,则被调查学生的平均分数为( )
A.3分 B.分 C.分 D.分
填空题(本大题共8小题,每小题4分,共32分)
11.用2、4、5三张卡片上的数字组成若干个不同的三位数,所有这些三位数的平均数是 .
12.在学校举行的大合唱比赛中,各班的总得分由演唱效果、动作编排、指挥能力依次按的比例计算.八年级(2)班上述三项得分分别为分,分,分,则该班的总得分为 分.
13.在2023年的体育考试中,盘州市某初中学校对某班八名学生的体育成绩进行统计并制作了如下表格,则通过表格,可知该组数据的中位数为 分.
人数/人 1 3 2 1 1
成绩/分 44 45 46 47 48
14.2023年9月25日,杭州亚运会男子10米气步枪个人决赛,我国18岁小将盛李豪打破世界纪录夺金.如图是盛李豪10次的射击成绩.这10次射击成绩的众数、中位数、平均数分别为 (按顺序填).
15.小林同学在上半学期的5次单元测验成绩分别为88、91、89、92、90,则他这5次测验的方差是 .
16.在杭州亚运会的跳水比赛中,对某运动员的第一个动作,8位裁判的打分如下(单位:分):9,,,,,,7,8,这组数据的极差是 .
17.八(3)资源文老师对甲、乙、丙3名同学进行诗词培训,计划从中选课一名同学参加“庆元几诗词大赛”,语文老师对甲、乙、丙三名同学进行了10次测试,测试成绩的平均数及方差如下表所示,若从这三名同学中选出一名成绩又高又稳定的参赛,则应选的是 .
甲 乙 丙
95 95 94
18 15 18
18.某学校开展“齐诵满江红,传承报国志”诵读比赛,八年级准备从小乐和小涵两位同学中选拔一位同学参加决赛,如图是小乐和小涵两位同学参加5次选拔赛的测试成绩(满分为100分)折线统计图,若选择一位成绩优异且稳定的同学参赛,推选参加决赛的同学是 (填“小乐”或“小涵”).
三、解答题(本大题共6小题,共58分)
19.(8分)自双减以来,同学们的课后延时服务活动丰富多彩,某学校在新的学期举办“篮球特色热爱篮核选拔班”,大量球的同学踊跃报名,但由于名额有限,所以需要考,考核的最终评价成绩由篮球知识、身体素质、篮球技能三项构成,下表是对甲、乙两名同学的成绩记录.
成绩/分
篮球知识 身体素质 篮球技能
甲 93 94 89
乙 88 90 95
(1)如果根据三项成绩的平均分确定最终评价成绩,计算说明谁将获胜;
(2)根据实际需要,将篮球知识、身体素质、篮球技能三项成绩按的比例确定最终评价成绩,计算说明谁将获胜;
(3)如果你是“篮球特色班”的老师,请你制定一项标准来确定获胜人选,并说明制定该标准的理由.
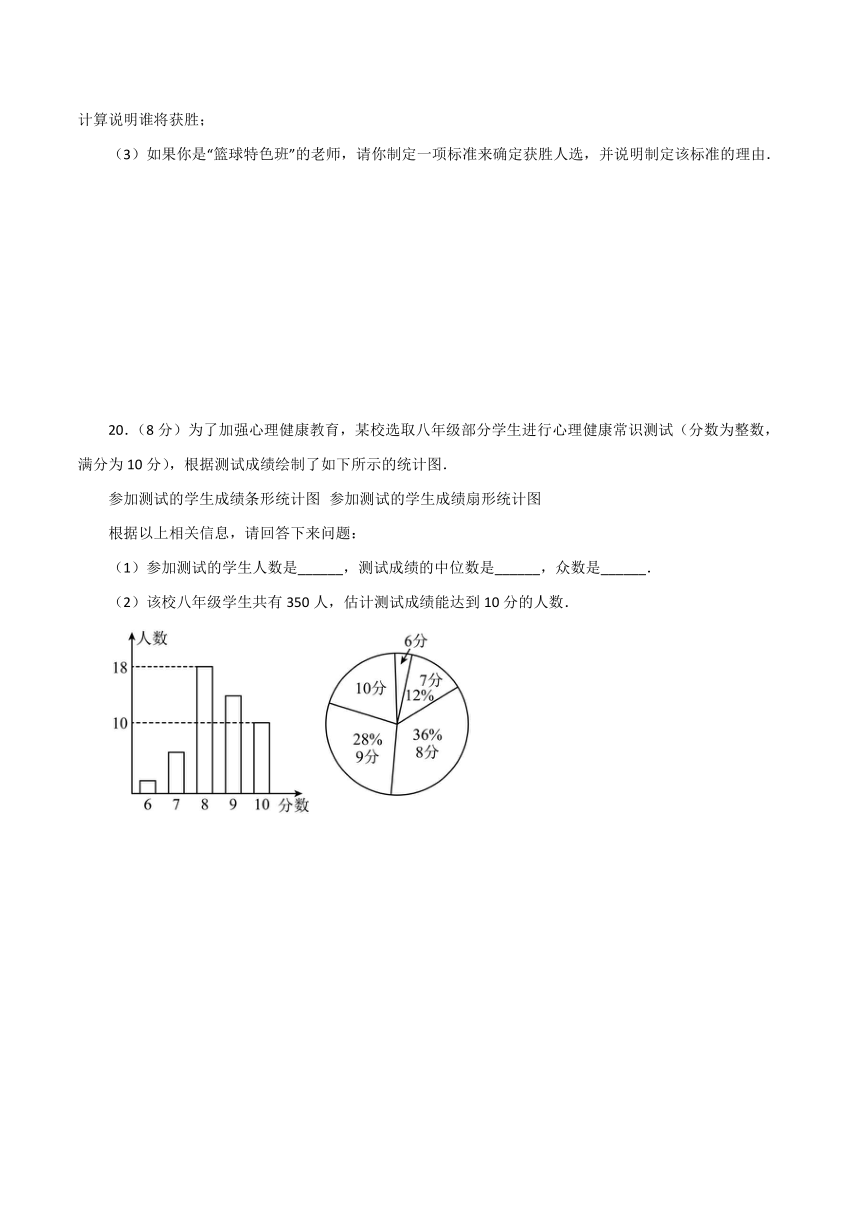
20.(8分)为了加强心理健康教育,某校选取八年级部分学生进行心理健康常识测试(分数为整数,满分为10分),根据测试成绩绘制了如下所示的统计图.
参加测试的学生成绩条形统计图 参加测试的学生成绩扇形统计图
根据以上相关信息,请回答下来问题:
(1)参加测试的学生人数是______,测试成绩的中位数是______,众数是______.
(2)该校八年级学生共有350人,估计测试成绩能达到10分的人数.
21.(10分)体育老师要从甲、乙两名跑步运动员中挑选一人参加校运动会比赛,在最近的6次选拔赛中,他们的成绩如下(单位:m):
甲 294 296 295 295 308 312
乙 295 296 307 300 302 300
(1)请你运用所学的统计知识做分析,从三个不同的角度评价甲、乙两人的跑步成绩;
(2)历届比赛表明:成绩达到300 m就有可能夺冠,为了夺冠,你认为应选择哪一名运动员参加这项比赛?历届比赛表明:成绩307达到就能打破记录,为了打破记录,你认为应选择哪一名运动员参加这项比赛?
22.(10分)某校要选派一名跳高运动员参加一项比赛活动,对甲、乙两名运动员进行了5次选拔活动,他们的成绩(单位:)如下:
甲:170,166,163,167,169
乙:161,172,163,171,168
(1)根据甲、乙两人成绩的平均数和中位数,说明哪个人的成绩较好;
(2)哪个人的成绩比较稳定?并说明理由.
23.(10分)调查背景:
陕西的秦岭山区、渭北早塬都是核桃优质产地,这里得天独厚的条件,让每株核桃树吸收了天地之灵气,日月之精华.小明的爸爸在这里承包了一个果园,种植了100棵核桃树,今年已进入收获期,小明想帮爸爸分析收成情况.
调查发现:
收获时,随机选取了部分核桃树作为样本,对所选取的每棵树上的核桃产量进行统计,并将得到的结果绘制了如图统计图.
实践探究:
分析数据如下:
平均数 中位数 众数
a b c
问题解决:
(1)通过计算补全条形统计图,并求m的值;
(2)填空:上述表中 , ;
(3)求表中a的值,并估算小明的爸爸种植的这100棵核桃树的总产量.
24.(12分)综合与实践
【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动,
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
【实践探究】分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 m 4.0 0.0424
荔枝树叶的长宽比 1.91 2.0 n 0.0669
【问题解决】
(1)上述表格中,________,________;
(2)①A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是________(填序号)
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树 并给出你的理由.
参考答案:
1.D
【分析】题目主要考查正负数的应用及平均分的计算,理解题意是解题关键.
解:A、最高成绩为分,选项错误,不符合题意;
B、最低成绩为分,选项错误,不符合题意;
C、,
平均分为分,选项错误,不符合题意;
D、平均分为分,选项正确,符合题意;
故选:D.
2.B
【分析】本题考查了加权平均数的定义,分式方程的应用,加权平均数:(其中);理解定义,掌握公式是解题的关键.
解:由题意得
,
解得:,
经检验:是所列方程的根;
故选:B.
3.C
【分析】本题考查中位,把一组数据按从小到大排列,当有偶数个数据时,中间两个数的平均数叫中位数,当有奇数个数据时,中间位置的数叫中位数.
根据中位数的定义 求解即可.
解:∵,
又∵这四个数字的中位数为2,
∴,
解得:.
故选:C.
4.C
【分析】根据统计图中的数据和题意,可以得到的值,本题得以解决.
解:由统计图可知,前3次的中位数是3,
第4次买的西瓜单价是元千克,这四个单价的中位数恰好也是众数,
,
故选:C.
【点拨】本题考查条形统计图、中位数、众数,解题的关键是明确题意,利用数形结合的思想解答.
5.C
【分析】本题主要考查平均数和样本容量的定义及方差,熟练掌握平均数和样本容量的定义及方差是解题的关键.
根据平均数的概念和样本容量指的是一个样本中所包含的单位数及方差公式的意义可直接进行求解.
解:∵一组数据的方差公式是
∴这组数据的平均数为45,样本容量为50.
故选C.
6.C
【分析】本题主要考查了中位数,平均数,众数,方差.根据中位数,平均数,众数,方差的意义,逐项判断即可求解.
解:∵每位同学的成绩都少记录了,
∴实际成绩与记录成绩相比,众数增加,方差不变,平均数增加,中位数增加,
故选:C.
7.B
【分析】本题考查了扇形统计图及相关计算,掌握在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与的比是关键.
解:A.该校学生阅读文章篇数的平均数为,故此选项错误;
B.阅读文章篇数为12的学生数量对应的扇形圆心角为,故此选项正确;
C.由扇形统计图可以看出该校学生阅读文章篇数的众数为15,故此选项错误;
D.由扇形统计图可以看出,该校有学生阅读文章的篇数大于15的仅占,没有占一半以上,故此选项错误;
故选:B.
8.A
【分析】本题主要考查了折线统计图、中位数、众数等知识点,从折线统计图中获取信息是解题的关键.
利用众数、中位数的定义结合折线统计图即可解答.
解:由折线统计图可知数据为:,2,,,3,3,3,4,
这些数据上3出现的次数最多,故众数为3,
数据从小到大排列:,,,2, 3,3,3,4,处于中间的数为2和3,故中位数为:.
故选:A.
9.B
【分析】本题主要考查了求加权平均数,用对应学科的分数乘以对应的权重求出每一科的分数,再求和,最后除以10即可得到答案,熟知加权平均数的定义是解题的关键.
解:由题意得,平均成绩为,
故选:B.
10.D
【分析】先根据A, D等级的人数和,及圆心角的度数和求出总人数,再根据各级的度数和总人数分别求出B 级、C 级的人数,最后根据平均数的计算公式即可求出答案.
解:A, D等级的人数和为人,圆心角的度数和为,
被调查学生的总人数为人,
B等级的人数人,
C等级的人数人,
则被调查学生的平均分数为分,
故选:D.
【点拨】此题考查了条形统计图与扇形统计图,根据A, D等级的人数和,及圆心角的度数和求出总人数是解题的关键.
11.407
【分析】先列举出所有可能组成的三位数,再求平均数即可.
解:根据题意可得:
2、4、5可以组成的三位数有:,
∴这些三位数的平均数,
故答案为:407.
【点拨】本题主要考查了求平均数,解题的关键是列举出所有可以组成的三位数,以及平均数的求法.
12.
【分析】本题考查了加权平均数.熟练掌握加权平均数是解题的关键.
根据,计算求解即可.
解:由题意知,该班总得分为(分),
故答案为:.
13.
【分析】本题主要考查了中位数的定义,熟练掌握中位数的定义是解题的关键.先求出总人数,得出中位数为第4个人和第5个人成绩的平均数,即可解答.
解:总人数:(人),
∴中位数为第4个人和第5个人成绩的平均数,
∴该组数据的中位数,
故答案为:.
14.10.6,10.6,10.6
【分析】根据众数、中位数、平均数的定义分别求解即可.
解:∵10次的射击成绩从小到大排列:10.3,10.4,10.5,10.6,10.6,10.6,10.7,10.7,10.8,10.8,
∴众数是10.6;
中位数是;
平均数是.
故答案为:10.6,10.6,10.6.
【点拨】本题考查了折线统计图,众数、中位数、平均数,熟练掌握众数、中位数、平均数的定义是解答本题的关键.
15.2
【分析】本题考查了求方程,先求出这组数据的平均数,再根据方程的定义“各个数据与平均数的差的平方的平均数”,即可求解.
解:,
,
故答案为:2.
16.2
【分析】本题考查极差的定义,根据数据中最大值与最小值之差叫极差即可得到答案;
解:由题意可得,
,
故答案为:2.
17.乙
【分析】本题考查了平均数和方差的应用;
根据方差越小越稳定进行判断即可.
解:∵,且,
∴这三名同学中成绩又高又稳定的是乙,
故答案为:乙.
18.小涵
【分析】分别计算出小乐和小涵成绩的平均成绩和方差,再根据平均成绩和方差确定成绩优异且稳定的同学参赛即可.
解:根据题意得:
,
,
,
,
,
小涵的成绩优异且稳定,
推选参加决赛的同学是小涵,
故答案为:小涵.
【点拨】本题考查了算术平均数和方差,熟练掌握算术平均数和方差的计算公式和意义是解题的关键.
19.(1)甲将获胜;(2)乙将获胜;(3)见分析
【分析】本题考查的知识点是算术平均数和加权平均数,掌握定义是解决问题的关键.
(1)利用算术平均数的定义求出甲、乙两名同学的成绩,再进行比较,即可得出答案;
(2)根据加权平均数的定义列出算式,求出甲、乙两名同学的成绩,再进行比较,即可得出答案;
(3)按第(2)问的标准即可.
(1)解:甲的成绩为(分),
乙的成绩为(分),
∵,
∴甲将获胜;
(2)解:甲的成绩为(分),
乙的成绩为(分),
∵,
∴乙将获胜;
(3)解:将篮球知识、身体素质、篮球技能三项成绩按的比例确定最终评价成绩,乙将获胜,
理由:因为是“篮球特色班”,要重点关注的是篮球技能,所以将篮球知识、身体素质、篮球技能三项成绩按的比例确定最终评价成绩.
20.(1)人数是50,中位数是8,众数是8;(2)八年级350名学生中,估计测试成绩有70人能达到10分.
【分析】本题考查扇形统计图与条形统计图的关联,从统计图中提取相关信息解题即可.
(1)利用分的人数除以所占百分比即可求出总人数,然后利用中位数和众数的定义解题即可;
(2)利用10分的人数所占百分比乘以八年级的人数即可解题.
(1)解:人,
9分的人数为人,
从大到小排列后居于中间的两个数分别为分和分,即中位数为,
在这组数据中出现的次数最多,即众数为,
故答案为:,,;
(2)解:人,
答:八年级350名学生中,估计测试成绩有70人能达到10分.
21.(1)见详解;(2)应选乙运动员夺冠,应选甲运动员打破记录
【分析】此题主要考查了方差的求法以及算术平均数公式,熟练地记忆方差公式是解决问题的关键.
(1)计算甲,乙两名运动员的平均数,中位数,方差,再进行比较说明,
(2)分析比较数据,再得出结论.
(1)解: ,
,,
从平均成绩的角度,甲,乙两名运动员的成绩一样好;
乙两名运动员的中位数分别是,,
从中位数的角度,乙运动员成绩好.
,
,
从方差的角度,乙运动员成绩较稳定.
(2)在这6次比赛中,乙运动员有4次成绩超成绩达到,而甲仅有2次,因此为了夺冠,应选乙运动员参加这项比赛.甲运动员的最好成绩是,乙运动员是,则为了打破记录,应选甲运动员.
22.(1)甲的平均成绩为167,中位数为167;乙的平均成绩为167,中位数为168;(2)甲的成绩比较稳定,理由见分析
【分析】本题考查了平均数、中位数和方差,解题的关键是掌握平均数、中位数和方差的计算方法.
(1)根据中位数和平均数的计算方法计算,然后根据平均数和中位数的意义作出判断即可;
(2)计算方差,方差越小越稳定.
(1)解:甲的成绩按由小到大的顺序排序:163,166,167,169,170,
处于中间的成绩为167,
甲的中位数为167,
甲的平均数:,
乙的成绩按由小到大的顺序排序:161,163,168,171,172,
处于中间的成绩为168,
乙的中位数为168,
乙的平均数:,
甲、乙的平均数相同,乙的中位数大于甲的中位数,
乙的成绩较好;
(2)解:甲的方差:
,
乙的方差:
,
甲的方差小于乙的方差,
甲的成绩稳定.
23.(1)统计图见分析,;(2)65;60;(3);
【分析】本题主要考查了求平均数,众数,中位数,用样本估计总体,扇形统计图与条形统计图信息相关联:
(1)用产量为的核桃树数量除以其数量占比求出选取的核桃树,进而求出产量为的核桃树,再根据频率频数总数求出m的值,进而补全统计图即可;
(2)根据中位数和众数的定义求解即可;
(3)先根据加权平均数的定义求出a的值,进而求出总产量即可.
(1)解:棵,
∴一共选取了20棵核桃树,
∴产量为的核桃树有棵,
∴,
∴,
补全统计图如下:
(2)解:∵产量为的核桃树最多,
∴众数,
将这20棵核桃树的产量从低到高排列,处在第10名和第11名的产量分别是、,
∴中位数,
故答案为:65;60;
(3)解:由题意得,,
,
∴估算小明的爸爸种植的这100棵核桃树的总产量为.
24.(1)3.75,2.0;(2)②;(3)这片树叶更可能来自于荔枝,理由见分析
【分析】(1)根据中位数和众数的定义求解即可;
(2)根据方差的定义,方差越小,形状差别越小,根据树叶的长宽比的平均数、中位数和众数来看,即可判断荔枝树叶的长宽比;
(3)计算该树叶的长宽比即可判断来自哪颗树.
解:(1)芒果树叶的长宽比中数据从小到大排序处在第5、6位的两个数的平均数为,因此中位数m=3.75;
荔枝树叶的长宽比中数据出现次数最多的是2.0,因此众数n=2.0;
故答案为:3.75,2.0;
(2)合理的是②,理由如下:从树叶的长宽比的方差来看,芒果树叶的长宽比的方差较小,所以芒果叶形状差别更小;从树叶的长宽比的平均数、中位数和众数来看,荔枝树叶的长宽比为2,所以荔枝树叶的长约为宽的两倍;
故答案为:②;
(3)这片树叶更可能来自荔枝,理由如下:
这片树叶长,宽 ,长宽比大约为2.0,
根据平均数这片树叶可能来自荔枝树.
【点拨】本题考查了统计图中中位数、众数、平均数、方差的意义,看懂统计图表,正确的计算是解决问题的关键.
一、单选题(本大题共10小题,每小题3分,共30分)
1.在一竞赛中,老师将90分规定为标准成绩,记作0分,高出此分记为正,不足此分记为负,五名参赛者的成绩:,,,,0.那么( )
A.最高成绩为90分 B.最低成绩为88分
C.平均分为90分 D.平均分为分
2.坚定不移听党话,跟党走,让红色基因、革命薪火代代传承,某校组织开展“从小学党史,永远跟党走”系列的知识竞赛,培育孩子们的爱党、爱国情怀.下表是该学校学习小组知识竞赛的成绩统计表:
成绩 86 90 98 100
人数 1 3 1
已知该学习小组本次知识竞赛的平均分是分,那么表中的x的值是( )
A.4 B.5 C.6 D.7
3.在三个数字0,1,5中,再加入一个大于0的数字,使这四个数字的中位数为2,则加入的数字x是( )
A.1 B.2 C.3 D.4
4.小明前3次购买的西瓜单价如图所示,若第4次买的西瓜单价是元/千克,且这4个单价的中位数与众数相同,则a 的值为( )
A.5 B.4 C.3 D.2
5.习近平总书记指出:“扶贫先扶志,扶贫必扶智”,某企业扶贫小组准备为贫困户送温暖活动,该企业对扶贫对象的年龄结构进行了随机抽样调查,调查所得的一组数据的方差公式是,则这组数据的平均数和样本容量分别是( )
A.50,45 B.50,28 C.45,50 D.45,36
6.体育委员小聪要帮体育老师分析本班的跳远成绩,将各统计量计算好后却发现由于场地布置失误,导致每位同学的成绩都少记录了,则实际成绩与记录成绩相比( )
A.众数改变,方差改变 B.众数不变,平均数改变
C.中位数改变,方差不变 D.中位数不变,平均数不变
7.2023年两会期间,某校组织开展了以“聚焦两会”为主题的阅读活动,如图所示的扇形统计图描述了该校学生一周内阅读关于两会文章的篇数情况,则下列说法正确的是( )
A.该校学生阅读文章篇数的平均数为
B.阅读文章篇数为12的学生数量对应的扇形圆心角为
C.该校学生阅读文章篇数的众数为18
D.该校有一半以上的学生阅读文章的篇数大于15
8.下图是在2023年12月28日预报的我区2024年1月24日到31日八天的最低气温()统计图,这八天最低气温的众数和中位数为( )
A.3,2.5 B.3,3 C.,2 D.3,2
9.“雷达图”是一种常用统计图,它可以直观展示一个研究对象的不同方面.图是某学生某次测验的五门学科成绩的“雷达图”,如果从学科一到学科五计算平均成绩,则该学生这五门学科的平均成绩是( )
A.80 B.82 C.84 D.86
10.某校组织学生进行绘画比赛,对参赛作品按A,B,C,D四个等级进行评定,四个等级的分数分别为A级5分,B级4分,C级2分,D级1分.现随机抽取部分学生绘画作品的评定结果进行分析,并根据各等级的人数绘制了如图所示的条形图和不完整的扇形图,条形图不小心被撕掉了一块,则被调查学生的平均分数为( )
A.3分 B.分 C.分 D.分
填空题(本大题共8小题,每小题4分,共32分)
11.用2、4、5三张卡片上的数字组成若干个不同的三位数,所有这些三位数的平均数是 .
12.在学校举行的大合唱比赛中,各班的总得分由演唱效果、动作编排、指挥能力依次按的比例计算.八年级(2)班上述三项得分分别为分,分,分,则该班的总得分为 分.
13.在2023年的体育考试中,盘州市某初中学校对某班八名学生的体育成绩进行统计并制作了如下表格,则通过表格,可知该组数据的中位数为 分.
人数/人 1 3 2 1 1
成绩/分 44 45 46 47 48
14.2023年9月25日,杭州亚运会男子10米气步枪个人决赛,我国18岁小将盛李豪打破世界纪录夺金.如图是盛李豪10次的射击成绩.这10次射击成绩的众数、中位数、平均数分别为 (按顺序填).
15.小林同学在上半学期的5次单元测验成绩分别为88、91、89、92、90,则他这5次测验的方差是 .
16.在杭州亚运会的跳水比赛中,对某运动员的第一个动作,8位裁判的打分如下(单位:分):9,,,,,,7,8,这组数据的极差是 .
17.八(3)资源文老师对甲、乙、丙3名同学进行诗词培训,计划从中选课一名同学参加“庆元几诗词大赛”,语文老师对甲、乙、丙三名同学进行了10次测试,测试成绩的平均数及方差如下表所示,若从这三名同学中选出一名成绩又高又稳定的参赛,则应选的是 .
甲 乙 丙
95 95 94
18 15 18
18.某学校开展“齐诵满江红,传承报国志”诵读比赛,八年级准备从小乐和小涵两位同学中选拔一位同学参加决赛,如图是小乐和小涵两位同学参加5次选拔赛的测试成绩(满分为100分)折线统计图,若选择一位成绩优异且稳定的同学参赛,推选参加决赛的同学是 (填“小乐”或“小涵”).
三、解答题(本大题共6小题,共58分)
19.(8分)自双减以来,同学们的课后延时服务活动丰富多彩,某学校在新的学期举办“篮球特色热爱篮核选拔班”,大量球的同学踊跃报名,但由于名额有限,所以需要考,考核的最终评价成绩由篮球知识、身体素质、篮球技能三项构成,下表是对甲、乙两名同学的成绩记录.
成绩/分
篮球知识 身体素质 篮球技能
甲 93 94 89
乙 88 90 95
(1)如果根据三项成绩的平均分确定最终评价成绩,计算说明谁将获胜;
(2)根据实际需要,将篮球知识、身体素质、篮球技能三项成绩按的比例确定最终评价成绩,计算说明谁将获胜;
(3)如果你是“篮球特色班”的老师,请你制定一项标准来确定获胜人选,并说明制定该标准的理由.
20.(8分)为了加强心理健康教育,某校选取八年级部分学生进行心理健康常识测试(分数为整数,满分为10分),根据测试成绩绘制了如下所示的统计图.
参加测试的学生成绩条形统计图 参加测试的学生成绩扇形统计图
根据以上相关信息,请回答下来问题:
(1)参加测试的学生人数是______,测试成绩的中位数是______,众数是______.
(2)该校八年级学生共有350人,估计测试成绩能达到10分的人数.
21.(10分)体育老师要从甲、乙两名跑步运动员中挑选一人参加校运动会比赛,在最近的6次选拔赛中,他们的成绩如下(单位:m):
甲 294 296 295 295 308 312
乙 295 296 307 300 302 300
(1)请你运用所学的统计知识做分析,从三个不同的角度评价甲、乙两人的跑步成绩;
(2)历届比赛表明:成绩达到300 m就有可能夺冠,为了夺冠,你认为应选择哪一名运动员参加这项比赛?历届比赛表明:成绩307达到就能打破记录,为了打破记录,你认为应选择哪一名运动员参加这项比赛?
22.(10分)某校要选派一名跳高运动员参加一项比赛活动,对甲、乙两名运动员进行了5次选拔活动,他们的成绩(单位:)如下:
甲:170,166,163,167,169
乙:161,172,163,171,168
(1)根据甲、乙两人成绩的平均数和中位数,说明哪个人的成绩较好;
(2)哪个人的成绩比较稳定?并说明理由.
23.(10分)调查背景:
陕西的秦岭山区、渭北早塬都是核桃优质产地,这里得天独厚的条件,让每株核桃树吸收了天地之灵气,日月之精华.小明的爸爸在这里承包了一个果园,种植了100棵核桃树,今年已进入收获期,小明想帮爸爸分析收成情况.
调查发现:
收获时,随机选取了部分核桃树作为样本,对所选取的每棵树上的核桃产量进行统计,并将得到的结果绘制了如图统计图.
实践探究:
分析数据如下:
平均数 中位数 众数
a b c
问题解决:
(1)通过计算补全条形统计图,并求m的值;
(2)填空:上述表中 , ;
(3)求表中a的值,并估算小明的爸爸种植的这100棵核桃树的总产量.
24.(12分)综合与实践
【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动,
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
【实践探究】分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 m 4.0 0.0424
荔枝树叶的长宽比 1.91 2.0 n 0.0669
【问题解决】
(1)上述表格中,________,________;
(2)①A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是________(填序号)
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树 并给出你的理由.
参考答案:
1.D
【分析】题目主要考查正负数的应用及平均分的计算,理解题意是解题关键.
解:A、最高成绩为分,选项错误,不符合题意;
B、最低成绩为分,选项错误,不符合题意;
C、,
平均分为分,选项错误,不符合题意;
D、平均分为分,选项正确,符合题意;
故选:D.
2.B
【分析】本题考查了加权平均数的定义,分式方程的应用,加权平均数:(其中);理解定义,掌握公式是解题的关键.
解:由题意得
,
解得:,
经检验:是所列方程的根;
故选:B.
3.C
【分析】本题考查中位,把一组数据按从小到大排列,当有偶数个数据时,中间两个数的平均数叫中位数,当有奇数个数据时,中间位置的数叫中位数.
根据中位数的定义 求解即可.
解:∵,
又∵这四个数字的中位数为2,
∴,
解得:.
故选:C.
4.C
【分析】根据统计图中的数据和题意,可以得到的值,本题得以解决.
解:由统计图可知,前3次的中位数是3,
第4次买的西瓜单价是元千克,这四个单价的中位数恰好也是众数,
,
故选:C.
【点拨】本题考查条形统计图、中位数、众数,解题的关键是明确题意,利用数形结合的思想解答.
5.C
【分析】本题主要考查平均数和样本容量的定义及方差,熟练掌握平均数和样本容量的定义及方差是解题的关键.
根据平均数的概念和样本容量指的是一个样本中所包含的单位数及方差公式的意义可直接进行求解.
解:∵一组数据的方差公式是
∴这组数据的平均数为45,样本容量为50.
故选C.
6.C
【分析】本题主要考查了中位数,平均数,众数,方差.根据中位数,平均数,众数,方差的意义,逐项判断即可求解.
解:∵每位同学的成绩都少记录了,
∴实际成绩与记录成绩相比,众数增加,方差不变,平均数增加,中位数增加,
故选:C.
7.B
【分析】本题考查了扇形统计图及相关计算,掌握在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与的比是关键.
解:A.该校学生阅读文章篇数的平均数为,故此选项错误;
B.阅读文章篇数为12的学生数量对应的扇形圆心角为,故此选项正确;
C.由扇形统计图可以看出该校学生阅读文章篇数的众数为15,故此选项错误;
D.由扇形统计图可以看出,该校有学生阅读文章的篇数大于15的仅占,没有占一半以上,故此选项错误;
故选:B.
8.A
【分析】本题主要考查了折线统计图、中位数、众数等知识点,从折线统计图中获取信息是解题的关键.
利用众数、中位数的定义结合折线统计图即可解答.
解:由折线统计图可知数据为:,2,,,3,3,3,4,
这些数据上3出现的次数最多,故众数为3,
数据从小到大排列:,,,2, 3,3,3,4,处于中间的数为2和3,故中位数为:.
故选:A.
9.B
【分析】本题主要考查了求加权平均数,用对应学科的分数乘以对应的权重求出每一科的分数,再求和,最后除以10即可得到答案,熟知加权平均数的定义是解题的关键.
解:由题意得,平均成绩为,
故选:B.
10.D
【分析】先根据A, D等级的人数和,及圆心角的度数和求出总人数,再根据各级的度数和总人数分别求出B 级、C 级的人数,最后根据平均数的计算公式即可求出答案.
解:A, D等级的人数和为人,圆心角的度数和为,
被调查学生的总人数为人,
B等级的人数人,
C等级的人数人,
则被调查学生的平均分数为分,
故选:D.
【点拨】此题考查了条形统计图与扇形统计图,根据A, D等级的人数和,及圆心角的度数和求出总人数是解题的关键.
11.407
【分析】先列举出所有可能组成的三位数,再求平均数即可.
解:根据题意可得:
2、4、5可以组成的三位数有:,
∴这些三位数的平均数,
故答案为:407.
【点拨】本题主要考查了求平均数,解题的关键是列举出所有可以组成的三位数,以及平均数的求法.
12.
【分析】本题考查了加权平均数.熟练掌握加权平均数是解题的关键.
根据,计算求解即可.
解:由题意知,该班总得分为(分),
故答案为:.
13.
【分析】本题主要考查了中位数的定义,熟练掌握中位数的定义是解题的关键.先求出总人数,得出中位数为第4个人和第5个人成绩的平均数,即可解答.
解:总人数:(人),
∴中位数为第4个人和第5个人成绩的平均数,
∴该组数据的中位数,
故答案为:.
14.10.6,10.6,10.6
【分析】根据众数、中位数、平均数的定义分别求解即可.
解:∵10次的射击成绩从小到大排列:10.3,10.4,10.5,10.6,10.6,10.6,10.7,10.7,10.8,10.8,
∴众数是10.6;
中位数是;
平均数是.
故答案为:10.6,10.6,10.6.
【点拨】本题考查了折线统计图,众数、中位数、平均数,熟练掌握众数、中位数、平均数的定义是解答本题的关键.
15.2
【分析】本题考查了求方程,先求出这组数据的平均数,再根据方程的定义“各个数据与平均数的差的平方的平均数”,即可求解.
解:,
,
故答案为:2.
16.2
【分析】本题考查极差的定义,根据数据中最大值与最小值之差叫极差即可得到答案;
解:由题意可得,
,
故答案为:2.
17.乙
【分析】本题考查了平均数和方差的应用;
根据方差越小越稳定进行判断即可.
解:∵,且,
∴这三名同学中成绩又高又稳定的是乙,
故答案为:乙.
18.小涵
【分析】分别计算出小乐和小涵成绩的平均成绩和方差,再根据平均成绩和方差确定成绩优异且稳定的同学参赛即可.
解:根据题意得:
,
,
,
,
,
小涵的成绩优异且稳定,
推选参加决赛的同学是小涵,
故答案为:小涵.
【点拨】本题考查了算术平均数和方差,熟练掌握算术平均数和方差的计算公式和意义是解题的关键.
19.(1)甲将获胜;(2)乙将获胜;(3)见分析
【分析】本题考查的知识点是算术平均数和加权平均数,掌握定义是解决问题的关键.
(1)利用算术平均数的定义求出甲、乙两名同学的成绩,再进行比较,即可得出答案;
(2)根据加权平均数的定义列出算式,求出甲、乙两名同学的成绩,再进行比较,即可得出答案;
(3)按第(2)问的标准即可.
(1)解:甲的成绩为(分),
乙的成绩为(分),
∵,
∴甲将获胜;
(2)解:甲的成绩为(分),
乙的成绩为(分),
∵,
∴乙将获胜;
(3)解:将篮球知识、身体素质、篮球技能三项成绩按的比例确定最终评价成绩,乙将获胜,
理由:因为是“篮球特色班”,要重点关注的是篮球技能,所以将篮球知识、身体素质、篮球技能三项成绩按的比例确定最终评价成绩.
20.(1)人数是50,中位数是8,众数是8;(2)八年级350名学生中,估计测试成绩有70人能达到10分.
【分析】本题考查扇形统计图与条形统计图的关联,从统计图中提取相关信息解题即可.
(1)利用分的人数除以所占百分比即可求出总人数,然后利用中位数和众数的定义解题即可;
(2)利用10分的人数所占百分比乘以八年级的人数即可解题.
(1)解:人,
9分的人数为人,
从大到小排列后居于中间的两个数分别为分和分,即中位数为,
在这组数据中出现的次数最多,即众数为,
故答案为:,,;
(2)解:人,
答:八年级350名学生中,估计测试成绩有70人能达到10分.
21.(1)见详解;(2)应选乙运动员夺冠,应选甲运动员打破记录
【分析】此题主要考查了方差的求法以及算术平均数公式,熟练地记忆方差公式是解决问题的关键.
(1)计算甲,乙两名运动员的平均数,中位数,方差,再进行比较说明,
(2)分析比较数据,再得出结论.
(1)解: ,
,,
从平均成绩的角度,甲,乙两名运动员的成绩一样好;
乙两名运动员的中位数分别是,,
从中位数的角度,乙运动员成绩好.
,
,
从方差的角度,乙运动员成绩较稳定.
(2)在这6次比赛中,乙运动员有4次成绩超成绩达到,而甲仅有2次,因此为了夺冠,应选乙运动员参加这项比赛.甲运动员的最好成绩是,乙运动员是,则为了打破记录,应选甲运动员.
22.(1)甲的平均成绩为167,中位数为167;乙的平均成绩为167,中位数为168;(2)甲的成绩比较稳定,理由见分析
【分析】本题考查了平均数、中位数和方差,解题的关键是掌握平均数、中位数和方差的计算方法.
(1)根据中位数和平均数的计算方法计算,然后根据平均数和中位数的意义作出判断即可;
(2)计算方差,方差越小越稳定.
(1)解:甲的成绩按由小到大的顺序排序:163,166,167,169,170,
处于中间的成绩为167,
甲的中位数为167,
甲的平均数:,
乙的成绩按由小到大的顺序排序:161,163,168,171,172,
处于中间的成绩为168,
乙的中位数为168,
乙的平均数:,
甲、乙的平均数相同,乙的中位数大于甲的中位数,
乙的成绩较好;
(2)解:甲的方差:
,
乙的方差:
,
甲的方差小于乙的方差,
甲的成绩稳定.
23.(1)统计图见分析,;(2)65;60;(3);
【分析】本题主要考查了求平均数,众数,中位数,用样本估计总体,扇形统计图与条形统计图信息相关联:
(1)用产量为的核桃树数量除以其数量占比求出选取的核桃树,进而求出产量为的核桃树,再根据频率频数总数求出m的值,进而补全统计图即可;
(2)根据中位数和众数的定义求解即可;
(3)先根据加权平均数的定义求出a的值,进而求出总产量即可.
(1)解:棵,
∴一共选取了20棵核桃树,
∴产量为的核桃树有棵,
∴,
∴,
补全统计图如下:
(2)解:∵产量为的核桃树最多,
∴众数,
将这20棵核桃树的产量从低到高排列,处在第10名和第11名的产量分别是、,
∴中位数,
故答案为:65;60;
(3)解:由题意得,,
,
∴估算小明的爸爸种植的这100棵核桃树的总产量为.
24.(1)3.75,2.0;(2)②;(3)这片树叶更可能来自于荔枝,理由见分析
【分析】(1)根据中位数和众数的定义求解即可;
(2)根据方差的定义,方差越小,形状差别越小,根据树叶的长宽比的平均数、中位数和众数来看,即可判断荔枝树叶的长宽比;
(3)计算该树叶的长宽比即可判断来自哪颗树.
解:(1)芒果树叶的长宽比中数据从小到大排序处在第5、6位的两个数的平均数为,因此中位数m=3.75;
荔枝树叶的长宽比中数据出现次数最多的是2.0,因此众数n=2.0;
故答案为:3.75,2.0;
(2)合理的是②,理由如下:从树叶的长宽比的方差来看,芒果树叶的长宽比的方差较小,所以芒果叶形状差别更小;从树叶的长宽比的平均数、中位数和众数来看,荔枝树叶的长宽比为2,所以荔枝树叶的长约为宽的两倍;
故答案为:②;
(3)这片树叶更可能来自荔枝,理由如下:
这片树叶长,宽 ,长宽比大约为2.0,
根据平均数这片树叶可能来自荔枝树.
【点拨】本题考查了统计图中中位数、众数、平均数、方差的意义,看懂统计图表,正确的计算是解决问题的关键.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
