浙教版数学九年级上册第四章相似三角形的性质及应用
文档属性
| 名称 | 浙教版数学九年级上册第四章相似三角形的性质及应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 50.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-01 00:00:00 | ||
图片预览


文档简介
相似三角形的性质及应用
八年(2)班 张宝丽 指导师:杨克湖
满足对应角相等,对应边成比例的两个三角形就是相似三角形。判定两个三角形相似的主要方法有:两边对应成比例且夹角相等;两角对应相等;三边对应成比例。如果是直角三角形,可用直接用斜边与一直角边对应成比例来判定。
相似三角形中,解决各种问题,主要去发现问题中条件和结论的特点。从而添补或修置什么辅助线,转化为相似三角形。
例1:如图1,在的内部选取一点P,过P点作三条分别与的三边平行的直线,这样所得的三个三角形的面积分别为4,9和49。求的面积。
分析:对于这种图形,图中有相似三角形以及平行四边形,以相似三角形性质C相似三角形的相似比等于周长的比,而相似比的平方等于它们的面积比,然后将线段进行代换,从而解开。
解:∵FG∥AC IH∥AB DE∥BC
∴∽∽∽
∵=4 =9 =49
∴DP:PE:HG=2:3:7
∵四边形BOPH与四边形PGEC为平行四边形
∴OP=BH PE=CG
∴BH:HG:CG=2:7:3
∴BC:HG=12:7
∴
∴=144
这道题目利用相似就能简便巧妙地化解出来,其实利用相似我可以发现图1还有其他的规律。
解:①∵例①中求得DF:IE:HG=2:3:7 BC:HG=12:7
∴AC:IE=12:3 AB:DF=12:2
∴
∴
②例①得:∵BH:HG:CG=2:7:3 DP=BH PE=CG
同理
∴
由此可得,对于一个图形,利用相似我们可发现许多规律。
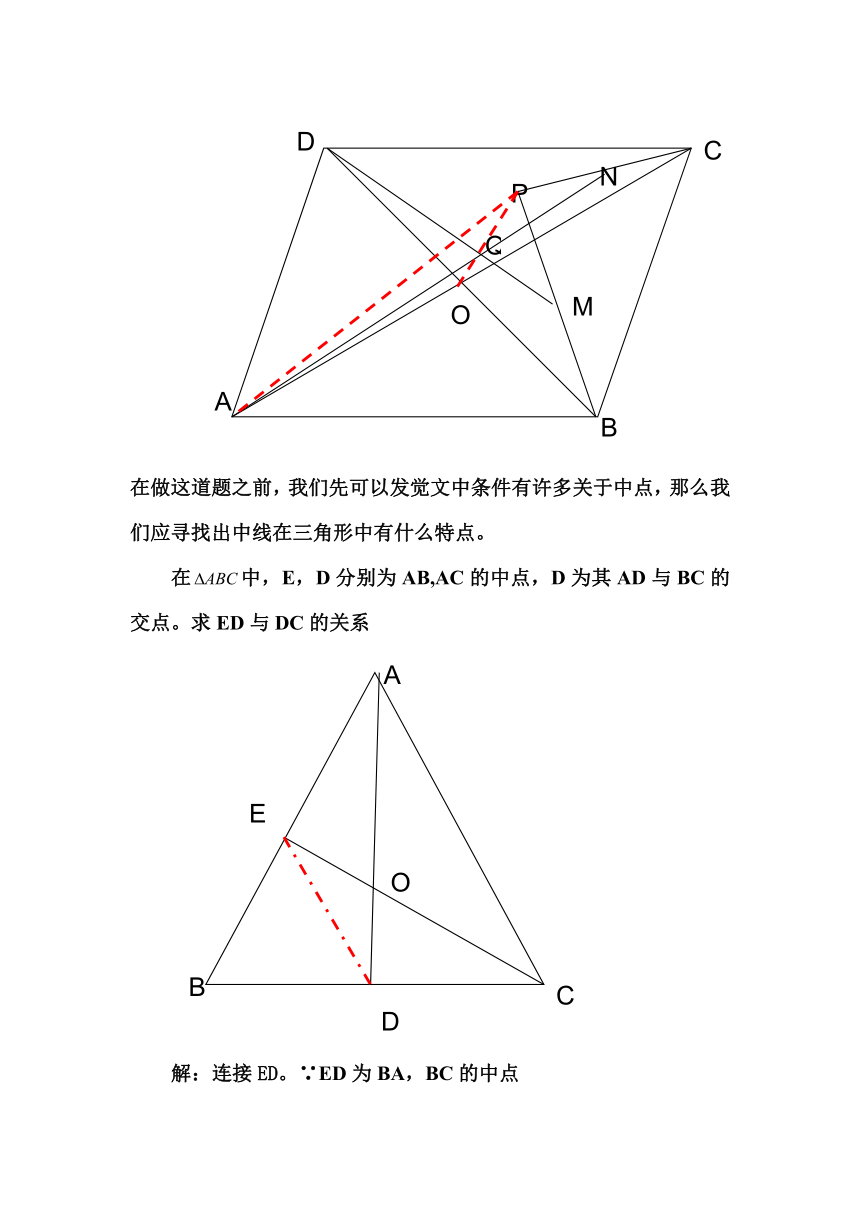
例2:如图2,已知P为平行四边形ABCD内一点,O为AC与BD的交点,M,N分别为PB,PC的中点,Q为AN与DM的交点。求证:(1)
P,Q,D三点在一条直线上;(2)PQ=2OQ。
在做这道题之前,我们先可以发觉文中条件有许多关于中点,那么我们应寻找出中线在三角形中有什么特点。
在中,E,D分别为AB,AC的中点,D为其AD与BC的交点。求ED与DC的关系
解:连接ED。∵ED为BA,BC的中点
∴BD= AC且BD平行AC
∴∽
∵
∴ED= OC
从而,我们以重心的特点来求这道题
证明:连接PO。设PO与AN,DM分别交与点Q1,Q2
∵四边形ABCD是平行四边形
∴AO=DO
∵M,N分别是PB,PC的中点
∴PN=NC 则Q为重心 ,PQ1=2Q2O
同理,PQ2=2OQ2
由此可得Q1与Q2重合,并且Q1,Q2就是AN,DM的交点。那么P,Q,O在一条直线上且PQ=2OQ
此题中,要证多点共线,图形来看好像很复杂,但只要巧妙的添
加几条辅助线,构成几个相似三角形,从而轻便地证出。这种方
法其实也可用于多线共点的问题,化繁为简。
然而,在我们的生活中,相似三角形与无所不在。在许多现
实生活中的问题,可以用相似三角形的特性,巧妙运用,求其距
离,相似三角形及比例线段在生活中有着广泛运用,人类第一次
运用相似原理进行测量。在2000多年钱,泰勒斯运用相似的原
理巧妙地测出了金字塔的高度,从而开拓了人们对这类问题的深
讨。
例3:如图4,有一批形状大小相同的不锈钢片,呈直角三角形。已知∠C=90 AB=5cm BC=3cm.试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片。求出这种正方形不锈钢片的边长。
分析:因为要在三角形中裁出最大的正方形,所以正方形的四个定点都应落在三角形的三边上。而正方形对边平行,而且对此就演绎出了相似,对于画法这有着不同的方案,所以我们应用方程思想求解。
解:如图,正方形EFGH边长为X,则AC=4,
而CD×AB=AC×BC=2,得CD=,又∽得
于是 解得x=
解如图,设正方形CFGH的边长为Ycm。有GH平行AC,得那么解得
∵
∴y>x
那应第二题的图那样裁剪,这时正方形S最大,它的边长为cm’
在讨论其类问题,也应考虑到多种情况,在利用相似来解最值。这是十分具有实际应用性的题型,可通过分析,推理,构思可能的方案。在通过比较,鉴别,筛选出最佳的设计方案,问题的多方面,多角度思考,呈现产生最佳设计方案的基本思想。
例4,在一块锐角三角形的余料上,加工成正方形零件,使正方形的四个顶点都在三角形边上,若三角形的三边长分别为a,b,c。且a>b>c.问正方形的两个顶点放在哪条边上可使加工出来的正方形零件面积最大?
解:设a,b,c三边上的高分别为,,。的面积为S,落在a,b,c三边上的正方形边长分别为,,。则=,=,=。作差比较得<<即当正方形的两个顶点放在最短边上可使正方形零件面积最大。
在这道题中,间接性巧妙地运用相似,附以面积,以及比较,便轻而易举地解出,求出最值。由此可见相似对于生产问题最值的应用。
G
H
E
I
D
F
P
C
B
A
Q
P
N
M
D
C
B
A
O
O
D
E
B
C
A
B
A
C
D
M
H
G
F
E
B
A
C
F
G
H
B
A
C
a
c
b
B
A
C
八年(2)班 张宝丽 指导师:杨克湖
满足对应角相等,对应边成比例的两个三角形就是相似三角形。判定两个三角形相似的主要方法有:两边对应成比例且夹角相等;两角对应相等;三边对应成比例。如果是直角三角形,可用直接用斜边与一直角边对应成比例来判定。
相似三角形中,解决各种问题,主要去发现问题中条件和结论的特点。从而添补或修置什么辅助线,转化为相似三角形。
例1:如图1,在的内部选取一点P,过P点作三条分别与的三边平行的直线,这样所得的三个三角形的面积分别为4,9和49。求的面积。
分析:对于这种图形,图中有相似三角形以及平行四边形,以相似三角形性质C相似三角形的相似比等于周长的比,而相似比的平方等于它们的面积比,然后将线段进行代换,从而解开。
解:∵FG∥AC IH∥AB DE∥BC
∴∽∽∽
∵=4 =9 =49
∴DP:PE:HG=2:3:7
∵四边形BOPH与四边形PGEC为平行四边形
∴OP=BH PE=CG
∴BH:HG:CG=2:7:3
∴BC:HG=12:7
∴
∴=144
这道题目利用相似就能简便巧妙地化解出来,其实利用相似我可以发现图1还有其他的规律。
解:①∵例①中求得DF:IE:HG=2:3:7 BC:HG=12:7
∴AC:IE=12:3 AB:DF=12:2
∴
∴
②例①得:∵BH:HG:CG=2:7:3 DP=BH PE=CG
同理
∴
由此可得,对于一个图形,利用相似我们可发现许多规律。
例2:如图2,已知P为平行四边形ABCD内一点,O为AC与BD的交点,M,N分别为PB,PC的中点,Q为AN与DM的交点。求证:(1)
P,Q,D三点在一条直线上;(2)PQ=2OQ。
在做这道题之前,我们先可以发觉文中条件有许多关于中点,那么我们应寻找出中线在三角形中有什么特点。
在中,E,D分别为AB,AC的中点,D为其AD与BC的交点。求ED与DC的关系
解:连接ED。∵ED为BA,BC的中点
∴BD= AC且BD平行AC
∴∽
∵
∴ED= OC
从而,我们以重心的特点来求这道题
证明:连接PO。设PO与AN,DM分别交与点Q1,Q2
∵四边形ABCD是平行四边形
∴AO=DO
∵M,N分别是PB,PC的中点
∴PN=NC 则Q为重心 ,PQ1=2Q2O
同理,PQ2=2OQ2
由此可得Q1与Q2重合,并且Q1,Q2就是AN,DM的交点。那么P,Q,O在一条直线上且PQ=2OQ
此题中,要证多点共线,图形来看好像很复杂,但只要巧妙的添
加几条辅助线,构成几个相似三角形,从而轻便地证出。这种方
法其实也可用于多线共点的问题,化繁为简。
然而,在我们的生活中,相似三角形与无所不在。在许多现
实生活中的问题,可以用相似三角形的特性,巧妙运用,求其距
离,相似三角形及比例线段在生活中有着广泛运用,人类第一次
运用相似原理进行测量。在2000多年钱,泰勒斯运用相似的原
理巧妙地测出了金字塔的高度,从而开拓了人们对这类问题的深
讨。
例3:如图4,有一批形状大小相同的不锈钢片,呈直角三角形。已知∠C=90 AB=5cm BC=3cm.试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片。求出这种正方形不锈钢片的边长。
分析:因为要在三角形中裁出最大的正方形,所以正方形的四个定点都应落在三角形的三边上。而正方形对边平行,而且对此就演绎出了相似,对于画法这有着不同的方案,所以我们应用方程思想求解。
解:如图,正方形EFGH边长为X,则AC=4,
而CD×AB=AC×BC=2,得CD=,又∽得
于是 解得x=
解如图,设正方形CFGH的边长为Ycm。有GH平行AC,得那么解得
∵
∴y>x
那应第二题的图那样裁剪,这时正方形S最大,它的边长为cm’
在讨论其类问题,也应考虑到多种情况,在利用相似来解最值。这是十分具有实际应用性的题型,可通过分析,推理,构思可能的方案。在通过比较,鉴别,筛选出最佳的设计方案,问题的多方面,多角度思考,呈现产生最佳设计方案的基本思想。
例4,在一块锐角三角形的余料上,加工成正方形零件,使正方形的四个顶点都在三角形边上,若三角形的三边长分别为a,b,c。且a>b>c.问正方形的两个顶点放在哪条边上可使加工出来的正方形零件面积最大?
解:设a,b,c三边上的高分别为,,。的面积为S,落在a,b,c三边上的正方形边长分别为,,。则=,=,=。作差比较得<<即当正方形的两个顶点放在最短边上可使正方形零件面积最大。
在这道题中,间接性巧妙地运用相似,附以面积,以及比较,便轻而易举地解出,求出最值。由此可见相似对于生产问题最值的应用。
G
H
E
I
D
F
P
C
B
A
Q
P
N
M
D
C
B
A
O
O
D
E
B
C
A
B
A
C
D
M
H
G
F
E
B
A
C
F
G
H
B
A
C
a
c
b
B
A
C
同课章节目录
