浙教版八年级数学下册第六章反比例函数单元复习题(含解析)
文档属性
| 名称 | 浙教版八年级数学下册第六章反比例函数单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 561.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 12:55:08 | ||
图片预览




文档简介
浙教版八年级数学下册第六章反比例函数单元复习题
一、选择题
1.反比例函数的比例系数为( )
A. B.-3 C.-5 D.
2.在反比例函数 中, 的取值范围是( )
A. B. C. D.
3.反比例函数y=的图象在第二、四象限,则k的取值范围是( )
A.k>0 B.k<0 C.k>1 D.k<1
4.对于函数y=,当x=2时,y=-5,则这个函数的表达式为( )
A.y= B.y= C.y= D.y=
5.对于反比例函数,下列说法不正确的是( )
A.点在它的图象上 B.它的图象在第二、四象限
C.当时,随的增大而增大 D.当时,随的增大而减小
6.若反比例函数 中, 与 的值相等, 则这个相等的值为( )
A.2 B. C. D.
7.已知反比例函数 ,当自变量 的值从3增加到6时,函数值减少了1,则函数的表达式为( )
A. B. C. D.
8.已知反比例函数y=﹣ ,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则﹣2<y<0
9.如图,在平面直角坐标系中,O为坐标原点,□OBAD的顶点 B 在反比例函数 的图像上,顶点 A 在反比例函数的图像上,顶点 D在x轴的负半轴上.若 OBAD 的面积是5,则k的值为 ( )
A.2 B.1 C.-1 D.-2
10.某校工作人员对教室进行消毒时,室内每立方米空气中的含药量y(毫升)与喷洒消毒液的时间x(分钟)成正比例关系,喷洒完成后,y与x成反比例关系(如图所示).已知喷洒消毒液用时6分钟,此时室内每立方米空气中的含药量为16毫升.问室内每立方米空气中的含药量不低于8毫升的持续时间为( )
A.7分钟 B.8分钟 C.9分钟 D.10分钟
二、填空题
11.若在反比例函数 的图象的每一条曲线上,y都随x的增大而减小,则m的取值范围是
12.若点在反比例函数图像上,则代数式 .
13.若正比例函数 y=kx(k≠0)与反比例函数 y= 的图像相交于A(x ,y ),B(x ,y )两点,则代数式 的值为 .
14.如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点,交轴于点,连结BO并延长交该反比例函数图象的另一支于点,连结AE交轴于点,连结BF,OA,且.
①若,则 .
②若,则的值为 .
三、解答题
15.已知函数 , 与x成正比例, 与x成反比例,且当 时, ;当 时, .求y与x的函数表达式.
16.已知y是x的反比例函数,且当x=2时,y=6.
(1)求y关于x的函数表达式.
(2)当x=4时,求y的值.
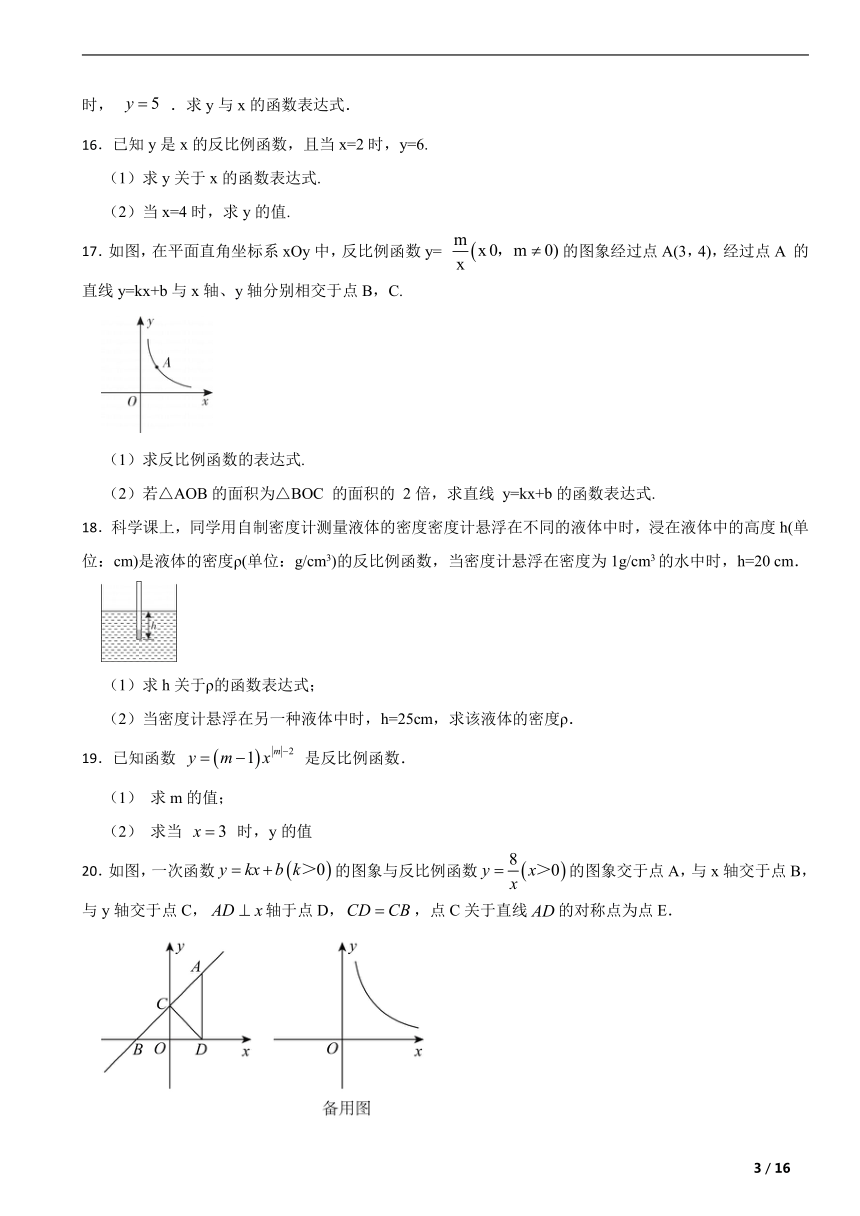
17.如图,在平面直角坐标系xOy中,反比例函数y= 的图象经过点A(3,4),经过点A 的直线y=kx+b与x轴、y轴分别相交于点B,C.
(1)求反比例函数的表达式.
(2)若△AOB的面积为△BOC 的面积的 2倍,求直线 y=kx+b的函数表达式.
18.科学课上,同学用自制密度计测量液体的密度密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1g/cm3的水中时,h=20 cm.
(1)求h关于ρ的函数表达式;
(2)当密度计悬浮在另一种液体中时,h=25cm,求该液体的密度ρ.
19.已知函数 是反比例函数.
(1)
求m的值;
(2)
求当 时,y的值
20.如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D,,点C关于直线的对称点为点E.
(1)点E是否在这个反比例函数的图象上?请说明理由;
(2)连接、,若四边形为正方形.
①求k、b的值;
②若点P在y轴上,当最大时,求点P的坐标.
21.为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为.
(1)若一次性燃烧完药物需10分钟.
①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式.
②当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时间段学生不能停留在教室里?
(2)已知室内每立方米空气中的含药量不低于时,才能有效消毒,如果有效消毒时间要持续120分钟,问要一次性燃烧完这种药物需多长时间?
22.如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y=的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m,0).其中m>0.
(1)四边形ABCD是 .(填写四边形ABCD的形状)
(2)当点A的坐标为(n,3)时,四边形ABCD是矩形,求m,n的值.
(3)试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:y=的比例系数为-.
故答案为:A.
【分析】反比例函数y=的比例系数为k,据此解答.
2.【答案】A
【解析】【解答】解:∵反比例函数y=,
∴m-1≠0,
∴m≠1.
故答案为:A.
【分析】根据反比例函数定义,满足函数关系y=(k≠0),得m-1≠0,求解即可得到m的范围.
3.【答案】D
【解析】【解答】解:依题意有:k-1<0,解得:k<1.
故答案为:D.
【分析】反比例函数中,当k>0时,图象位于第一、三象限;当k<0时,图象位于第二、四象限.
4.【答案】C
【解析】【解答】解:把 x=2时,y=-5 代入得,
解得k=-10,故.
故答案为:C.
【分析】将代入 函数y=即可求得k的值.
5.【答案】D
【解析】【解答】解:A、将x=-2代入函数,得到y=1,则(-2,1)在它的图像上,故A项正确,不符合题意;
B、根据反比例函数画出图象,可得图象在第二,四象限,故B项正确,不符合题意
C、根据图象可得当x>0时,y随x的增大而增大,故C项正确,不符合题意;
D、根据图象,当x<0时,y随x的增大而减小,故D项错误,符合题意.
故答案为:D.
【分析】我们可以利用反比例函数图象上点的坐标特征和反比例函数的性质对A、B、C、D,进行判断.
6.【答案】B
【解析】【解答】解:∵在反比例函数y=中,x=y,
∴x2=2,
∴x=y=±.
故答案为:B.
【分析】将x=y代入反比例函数解析式中,得x2=2,再开方即可求得x=y的值.
7.【答案】A
【解析】【解答】解:∵已知反比例函数,当自变量 的值从3增加到6时,函数值减少了1,
∴1=-,
∴k=6,
∴反比例函数的解析式为y=.
故答案为:A.
【分析】由反比例函数,当自变量 的值从3增加到6时,函数值减少了1,可列关于k的方程,解出k,即可求得反比例函数的表达式.
8.【答案】B
【解析】【解答】解: A、把点(-1,2)代入反比例函数y= ,得2=2成立,故说法正确,不符合题意;
B、∵k= <0,函数位于二、四象限,在每一象限y随x的增大而增大,故答案为:错误,符合题意;
C、∵k=-2<0,∴它的图象在第二、四象限,故说法正确,不符合题意;
D、当x=1时,y=-2,故当x>1时,-2<y<0说法正确,不符合题意;
故答案为:B.
【分析】根据反比例函数的性质,k= <0,函数位于二、四象限,在每一象限y随x的增大而增大,反比例函数的图象是中心对称图形解答.
9.【答案】D
【解析】【解答】解:如图,连接AO,设AB交y轴于点C,
∵四边形OBAD是平行四边形,OD在x轴上,平行四边形OBAD的面积为5,
∴AB∥x轴,S△AOB=2.5
∴AB⊥y轴,
∴S△AOC=|k|,S△BOC=1.5,
∴S△AOB=S△AOC+S△BOC,
∴|k|+1.5=2.5
∴k=±2,
∵ 反比例函数 的图象经过第二象限,
∴k=-2.
故答案为:D.
【分析】由平行四边形的性质得AB∥x轴,S△AOB=2.5,根据平行线的性质易得AB⊥y轴,根据反比例函数k的几何意义可得S△AOC=|k|,S△BOC=1.5,然后根据S△AOB=S△AOC+S△BOC建立方程,可求出k的值,最后结合反比例函数图象所在的象限可得答案.
10.【答案】C
【解析】【解答】解:当0≤x≤6时,设y=mx,
将点(6,16)代入得:6m=16,解得m=,
∴y=x,
当x>6时,设y=,
将点(6,16)代入得n=6×16=96,
∴y=,
∴y=,
若y=8,则y=x=8,y==8,
解得:x=3,x=12,
∴12-3=9(分钟),
∴ 问室内每立方米空气中的含药量不低于8毫升的持续时间为9分钟.
故答案为:C.
【分析】分别求出0≤x≤6和x>6时的函数解析式,再两个函数解析式中分别求出y=8时的x值,继而求解.
11.【答案】m>2
【解析】【解答】解:∵ 在反比例函数 的图象的每一条曲线上,y都随x的增大而减小 ,
∴m-2>0,
解得m>2.
故答案为:m>2.
【分析】由反比例函数图形的性质可得m-2>0,解之即可.
12.【答案】
【解析】【解答】解:点A(a,b)在反比例函数y=-上,
b=-,即ab=-3,
ab-1=-3-1=-4,
故答案为:-4
【分析】根据函数图象上的点的坐标与函数的关系求出ab的值,代入ab-1即可求解.
13.【答案】-2
【解析】【解答】解:∵反比例函数经过点A(x ,y ),B(x ,y ),
∴x1y1=1,x2y2=1,
∵ 正比例函数y=kx(k≠0)与反比例函数y= 的图像相交于A(x ,y ),B(x ,y )两点,
∴点A与点B关于坐标原点对称,
∴x1=-x2,
∴x1y2+x2y1=-x2y2-x1y1=-1-1=-2.
故答案为:-2.
【分析】根据反比例函数图象上任意一点的横纵坐标的乘积等于比例系数可得x1y1=1,x2y2=1,进而根据反比例函数的对称性可得x1=-x2,从而根据等量代换及整体代入可求解.
14.【答案】;10
【解析】【解答】①先设点A,B的横坐标分别为a,b,代入反比例函数可得A,B,
则可求出AB直线的方程为,
将x=0代入方程,
可得到点D,
又因为AB=AD,
所以,
化简得b=2a,,,,,
②因为B,E关于点O对称,则点E坐标为,
可以求出AC直线的方程为,
将x=0代入方程得到点F坐标为,
根据上题中b=2a,得,,
则k=10.
故答案为:;10.
【分析】①本题主要考查反比例函数,一次函数的求解,首先设点A,B的坐标,可求出AB直线的方程,从而表示出点D的坐标,化简可得;②与上题同理,利用点A.E求出AE直线的方程,可表示出点F的坐标,从而求得k的解。
15.【答案】解:∵ 与x成正比例, 与x成反比例∴可设 =mx, = ∴ =mx + 把 时, ; 时, 代入,得 解得 ∴y与x的函数关系式是 .
【解析】【分析】因为 与x成正比例, 与x成反比例,所以可设=mx,=,根据 y =+可得 y=mx+,再把x = 1 时, y = 4 ; x = 2 时, y = 5 代入上式可得关于m、n的二元一次方程组,解这个方程组即可求出m、n的值,则y与x的函数关系式可求。
16.【答案】(1)
(2)3
【解析】【解答】解:
∵ 当x =2时,y=6
∴ k= xy = 12
所以y关于x的函数解析式为:y=
(2)当x=4时,代入y=
得
所以当x=4时,y的值为3.
【分析】(1)通过待定系数法求出反比例函数解析式,(2)将x=4代入解析式,求出y值即可.
17.【答案】(1)
(2)或y=2x-2
【解析】【解答】解:
【分析】
18.【答案】(1)解: 设h关于ρ的函数表达式为h=
把p=1,h=20代人表达式,得k=1×20=20,
∴ h关于p的函数表达式为h= .
(2)解: 把h=25代人h= ,得25= ,
解得ρ=0.8,即该液体的密度ρ为0.8 g/cm3.
【解析】【分析】(1)利用待定系数法求出 浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数关系式即可;
(2)利用(1)解析式,求出h=25时的ρ值即可.
19.【答案】(1)解: 且 ,
解得: 且 ,
∴ .
(2)解:当 时,原方程变为 ,
当 时, .
【解析】【分析】(1)反比例函数可表示为y=kx-1(k≠0);所以可得-2=0,m-1≠0;计算即可求解;
(2)由题意把x=3代入(1)中求得的解析式计算即可求解;
20.【答案】(1)解:点E在这个反比例函数的图象上,
理由:∵一次函数的图象与反比例函数的图象交于点A,
∴设点A的坐标为,
∵点C关于直线AD的对称点为点E,
∴,平分CE,
如图.连接CE交AD于H,
∴,
∵,,
∴,
∴,
∵轴于D,
∴轴,
∴,
∵,
∴点E在这个反比例函数的图象上;
(2)解:①∵四边形ACDE为正方形,
∴,垂直平分,
∴,
设点A的坐标为,
∴,,
∴,
∴(负值舍去),
∴,,
把,代入得,
∴;
②延长交y轴于P,
∵,,
∴点B与点D关于y轴对称,
∴,
则点P即为符合条件的点,
由①知,,,
∴,,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
当时,,
∴.
故当最大时,点P的坐标为.
【解析】【分析】本题考查反比例函数、正方形的性质、轴对称的性质等知识点,
(1)根据轴对称的性质,设点A的坐标为,可以得出,平分,然后作图连接交于H,求出点,即可说明点E在这个反比例函数的图象上;
(2)①根据正方形的性质得出,垂直平分,设出点A的坐标为,求出点A、点C的坐标代入,即可求出k、b的值;
②作图,延长交y轴于P,得出点B与点D关于y轴对称,则点P即为符合条件的点,再根据①中求出的A、C坐标可求出a、n的值,从而得到直线的解析式即可求解.
21.【答案】(1)解:①设药物燃烧时的函数解析式为,药物燃烧后的解析式为,
把代入中得:,
∴,
∴药物燃烧时的函数解析式为,
∴药物刚好燃烧完时教室内每立方米空气含药量为,
把代入中得:,
∴,
∴药物燃烧后的解析式为;
②在中,当时,,
∵,
∴当时,y随x增大而增大,
∴当时,学生不能在教室停留;
在中,当时,,
∵,
∴当时,y随x增大而减小,
∴当时,学生不能在教室停留;
综上所述,当时,学生不能在教室停留;
(2)解:设要一次性燃烧完这种药物需t分钟,
同理可得当时,,
当药物刚好燃烧完时教室内每立方米空气含药量为,
同理可得时,,
在中,当时,,
∴当时为有效消毒时间;
在中,当时,,
∴当时为有效消毒时间;
综上所述,当时为有效消毒时间,
∵有效消毒时间为120分钟,
∴,
解得(负值舍去),
∴要一次性燃烧完这种药物需11分钟.
【解析】【分析】(1) ① 先利用待定系数法求出药物燃烧时的函数解析式为,进而求出药物刚好燃烧完时教室内每立方米空气含药量为7mg,从而即可利用待定系数法求出药物燃烧后的解析式;② 分别求出药物燃烧时和药物燃烧后,时x的值即可得到答案;
(2)设要一次性燃烧完这种药物需t分钟,仿照(1)①求出对应时间段的函数解析式,进而求出当y=0.7时x的值,再根据有效消毒时间为120分钟建立方程求解即可.
22.【答案】(1)平行四边形
(2)解:把A(n,3) 代入 y= 中,得3n=3,
∴n=1,
∴A(1,3),
∴OA=,
∵ 四边形ABCD是矩形 ,
∴OB=OA=,
∴m=;
(3)不能,理由如下:
∵点A在第一象限,B在x轴上,
∴∠AOB<90°,即得AC与BD不可能垂直,
∴ 四边形ABCD不能成为菱形 ;
【解析】【解答】解:(1)∵ 正比例函数y=kx(k>0)与反比例函数y=的图象分别交于A、C两点,
∴点A、C关于原点对称,即OA=OC,
∵点B与点D关于坐标原点O成中心对称 ,
∴OB=OD,
∴ 四边形ABCD是平行四边形;
故答案为:平行四边形.
【分析】(1)根据正比例函数与反比例函数的对称性可知OA=OC,结合题意知OB=OD,根据对角线互相平分可证四边形ABCD是平行四边形;
(2)将A(n,3) 代入 y= 中求出n值,即得A(1,3),利用勾股定理求出OA的长,根据矩形的性质可得OB=OA,据此即得m值;
(3)由点A在第一象限,B在x轴上,可知∠AOB<90°,即得AC与BD不可能垂直,根据菱形的性质即可判断.
1 / 1
一、选择题
1.反比例函数的比例系数为( )
A. B.-3 C.-5 D.
2.在反比例函数 中, 的取值范围是( )
A. B. C. D.
3.反比例函数y=的图象在第二、四象限,则k的取值范围是( )
A.k>0 B.k<0 C.k>1 D.k<1
4.对于函数y=,当x=2时,y=-5,则这个函数的表达式为( )
A.y= B.y= C.y= D.y=
5.对于反比例函数,下列说法不正确的是( )
A.点在它的图象上 B.它的图象在第二、四象限
C.当时,随的增大而增大 D.当时,随的增大而减小
6.若反比例函数 中, 与 的值相等, 则这个相等的值为( )
A.2 B. C. D.
7.已知反比例函数 ,当自变量 的值从3增加到6时,函数值减少了1,则函数的表达式为( )
A. B. C. D.
8.已知反比例函数y=﹣ ,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则﹣2<y<0
9.如图,在平面直角坐标系中,O为坐标原点,□OBAD的顶点 B 在反比例函数 的图像上,顶点 A 在反比例函数的图像上,顶点 D在x轴的负半轴上.若 OBAD 的面积是5,则k的值为 ( )
A.2 B.1 C.-1 D.-2
10.某校工作人员对教室进行消毒时,室内每立方米空气中的含药量y(毫升)与喷洒消毒液的时间x(分钟)成正比例关系,喷洒完成后,y与x成反比例关系(如图所示).已知喷洒消毒液用时6分钟,此时室内每立方米空气中的含药量为16毫升.问室内每立方米空气中的含药量不低于8毫升的持续时间为( )
A.7分钟 B.8分钟 C.9分钟 D.10分钟
二、填空题
11.若在反比例函数 的图象的每一条曲线上,y都随x的增大而减小,则m的取值范围是
12.若点在反比例函数图像上,则代数式 .
13.若正比例函数 y=kx(k≠0)与反比例函数 y= 的图像相交于A(x ,y ),B(x ,y )两点,则代数式 的值为 .
14.如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点,交轴于点,连结BO并延长交该反比例函数图象的另一支于点,连结AE交轴于点,连结BF,OA,且.
①若,则 .
②若,则的值为 .
三、解答题
15.已知函数 , 与x成正比例, 与x成反比例,且当 时, ;当 时, .求y与x的函数表达式.
16.已知y是x的反比例函数,且当x=2时,y=6.
(1)求y关于x的函数表达式.
(2)当x=4时,求y的值.
17.如图,在平面直角坐标系xOy中,反比例函数y= 的图象经过点A(3,4),经过点A 的直线y=kx+b与x轴、y轴分别相交于点B,C.
(1)求反比例函数的表达式.
(2)若△AOB的面积为△BOC 的面积的 2倍,求直线 y=kx+b的函数表达式.
18.科学课上,同学用自制密度计测量液体的密度密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1g/cm3的水中时,h=20 cm.
(1)求h关于ρ的函数表达式;
(2)当密度计悬浮在另一种液体中时,h=25cm,求该液体的密度ρ.
19.已知函数 是反比例函数.
(1)
求m的值;
(2)
求当 时,y的值
20.如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D,,点C关于直线的对称点为点E.
(1)点E是否在这个反比例函数的图象上?请说明理由;
(2)连接、,若四边形为正方形.
①求k、b的值;
②若点P在y轴上,当最大时,求点P的坐标.
21.为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为.
(1)若一次性燃烧完药物需10分钟.
①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式.
②当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时间段学生不能停留在教室里?
(2)已知室内每立方米空气中的含药量不低于时,才能有效消毒,如果有效消毒时间要持续120分钟,问要一次性燃烧完这种药物需多长时间?
22.如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y=的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m,0).其中m>0.
(1)四边形ABCD是 .(填写四边形ABCD的形状)
(2)当点A的坐标为(n,3)时,四边形ABCD是矩形,求m,n的值.
(3)试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:y=的比例系数为-.
故答案为:A.
【分析】反比例函数y=的比例系数为k,据此解答.
2.【答案】A
【解析】【解答】解:∵反比例函数y=,
∴m-1≠0,
∴m≠1.
故答案为:A.
【分析】根据反比例函数定义,满足函数关系y=(k≠0),得m-1≠0,求解即可得到m的范围.
3.【答案】D
【解析】【解答】解:依题意有:k-1<0,解得:k<1.
故答案为:D.
【分析】反比例函数中,当k>0时,图象位于第一、三象限;当k<0时,图象位于第二、四象限.
4.【答案】C
【解析】【解答】解:把 x=2时,y=-5 代入得,
解得k=-10,故.
故答案为:C.
【分析】将代入 函数y=即可求得k的值.
5.【答案】D
【解析】【解答】解:A、将x=-2代入函数,得到y=1,则(-2,1)在它的图像上,故A项正确,不符合题意;
B、根据反比例函数画出图象,可得图象在第二,四象限,故B项正确,不符合题意
C、根据图象可得当x>0时,y随x的增大而增大,故C项正确,不符合题意;
D、根据图象,当x<0时,y随x的增大而减小,故D项错误,符合题意.
故答案为:D.
【分析】我们可以利用反比例函数图象上点的坐标特征和反比例函数的性质对A、B、C、D,进行判断.
6.【答案】B
【解析】【解答】解:∵在反比例函数y=中,x=y,
∴x2=2,
∴x=y=±.
故答案为:B.
【分析】将x=y代入反比例函数解析式中,得x2=2,再开方即可求得x=y的值.
7.【答案】A
【解析】【解答】解:∵已知反比例函数,当自变量 的值从3增加到6时,函数值减少了1,
∴1=-,
∴k=6,
∴反比例函数的解析式为y=.
故答案为:A.
【分析】由反比例函数,当自变量 的值从3增加到6时,函数值减少了1,可列关于k的方程,解出k,即可求得反比例函数的表达式.
8.【答案】B
【解析】【解答】解: A、把点(-1,2)代入反比例函数y= ,得2=2成立,故说法正确,不符合题意;
B、∵k= <0,函数位于二、四象限,在每一象限y随x的增大而增大,故答案为:错误,符合题意;
C、∵k=-2<0,∴它的图象在第二、四象限,故说法正确,不符合题意;
D、当x=1时,y=-2,故当x>1时,-2<y<0说法正确,不符合题意;
故答案为:B.
【分析】根据反比例函数的性质,k= <0,函数位于二、四象限,在每一象限y随x的增大而增大,反比例函数的图象是中心对称图形解答.
9.【答案】D
【解析】【解答】解:如图,连接AO,设AB交y轴于点C,
∵四边形OBAD是平行四边形,OD在x轴上,平行四边形OBAD的面积为5,
∴AB∥x轴,S△AOB=2.5
∴AB⊥y轴,
∴S△AOC=|k|,S△BOC=1.5,
∴S△AOB=S△AOC+S△BOC,
∴|k|+1.5=2.5
∴k=±2,
∵ 反比例函数 的图象经过第二象限,
∴k=-2.
故答案为:D.
【分析】由平行四边形的性质得AB∥x轴,S△AOB=2.5,根据平行线的性质易得AB⊥y轴,根据反比例函数k的几何意义可得S△AOC=|k|,S△BOC=1.5,然后根据S△AOB=S△AOC+S△BOC建立方程,可求出k的值,最后结合反比例函数图象所在的象限可得答案.
10.【答案】C
【解析】【解答】解:当0≤x≤6时,设y=mx,
将点(6,16)代入得:6m=16,解得m=,
∴y=x,
当x>6时,设y=,
将点(6,16)代入得n=6×16=96,
∴y=,
∴y=,
若y=8,则y=x=8,y==8,
解得:x=3,x=12,
∴12-3=9(分钟),
∴ 问室内每立方米空气中的含药量不低于8毫升的持续时间为9分钟.
故答案为:C.
【分析】分别求出0≤x≤6和x>6时的函数解析式,再两个函数解析式中分别求出y=8时的x值,继而求解.
11.【答案】m>2
【解析】【解答】解:∵ 在反比例函数 的图象的每一条曲线上,y都随x的增大而减小 ,
∴m-2>0,
解得m>2.
故答案为:m>2.
【分析】由反比例函数图形的性质可得m-2>0,解之即可.
12.【答案】
【解析】【解答】解:点A(a,b)在反比例函数y=-上,
b=-,即ab=-3,
ab-1=-3-1=-4,
故答案为:-4
【分析】根据函数图象上的点的坐标与函数的关系求出ab的值,代入ab-1即可求解.
13.【答案】-2
【解析】【解答】解:∵反比例函数经过点A(x ,y ),B(x ,y ),
∴x1y1=1,x2y2=1,
∵ 正比例函数y=kx(k≠0)与反比例函数y= 的图像相交于A(x ,y ),B(x ,y )两点,
∴点A与点B关于坐标原点对称,
∴x1=-x2,
∴x1y2+x2y1=-x2y2-x1y1=-1-1=-2.
故答案为:-2.
【分析】根据反比例函数图象上任意一点的横纵坐标的乘积等于比例系数可得x1y1=1,x2y2=1,进而根据反比例函数的对称性可得x1=-x2,从而根据等量代换及整体代入可求解.
14.【答案】;10
【解析】【解答】①先设点A,B的横坐标分别为a,b,代入反比例函数可得A,B,
则可求出AB直线的方程为,
将x=0代入方程,
可得到点D,
又因为AB=AD,
所以,
化简得b=2a,,,,,
②因为B,E关于点O对称,则点E坐标为,
可以求出AC直线的方程为,
将x=0代入方程得到点F坐标为,
根据上题中b=2a,得,,
则k=10.
故答案为:;10.
【分析】①本题主要考查反比例函数,一次函数的求解,首先设点A,B的坐标,可求出AB直线的方程,从而表示出点D的坐标,化简可得;②与上题同理,利用点A.E求出AE直线的方程,可表示出点F的坐标,从而求得k的解。
15.【答案】解:∵ 与x成正比例, 与x成反比例∴可设 =mx, = ∴ =mx + 把 时, ; 时, 代入,得 解得 ∴y与x的函数关系式是 .
【解析】【分析】因为 与x成正比例, 与x成反比例,所以可设=mx,=,根据 y =+可得 y=mx+,再把x = 1 时, y = 4 ; x = 2 时, y = 5 代入上式可得关于m、n的二元一次方程组,解这个方程组即可求出m、n的值,则y与x的函数关系式可求。
16.【答案】(1)
(2)3
【解析】【解答】解:
∵ 当x =2时,y=6
∴ k= xy = 12
所以y关于x的函数解析式为:y=
(2)当x=4时,代入y=
得
所以当x=4时,y的值为3.
【分析】(1)通过待定系数法求出反比例函数解析式,(2)将x=4代入解析式,求出y值即可.
17.【答案】(1)
(2)或y=2x-2
【解析】【解答】解:
【分析】
18.【答案】(1)解: 设h关于ρ的函数表达式为h=
把p=1,h=20代人表达式,得k=1×20=20,
∴ h关于p的函数表达式为h= .
(2)解: 把h=25代人h= ,得25= ,
解得ρ=0.8,即该液体的密度ρ为0.8 g/cm3.
【解析】【分析】(1)利用待定系数法求出 浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数关系式即可;
(2)利用(1)解析式,求出h=25时的ρ值即可.
19.【答案】(1)解: 且 ,
解得: 且 ,
∴ .
(2)解:当 时,原方程变为 ,
当 时, .
【解析】【分析】(1)反比例函数可表示为y=kx-1(k≠0);所以可得-2=0,m-1≠0;计算即可求解;
(2)由题意把x=3代入(1)中求得的解析式计算即可求解;
20.【答案】(1)解:点E在这个反比例函数的图象上,
理由:∵一次函数的图象与反比例函数的图象交于点A,
∴设点A的坐标为,
∵点C关于直线AD的对称点为点E,
∴,平分CE,
如图.连接CE交AD于H,
∴,
∵,,
∴,
∴,
∵轴于D,
∴轴,
∴,
∵,
∴点E在这个反比例函数的图象上;
(2)解:①∵四边形ACDE为正方形,
∴,垂直平分,
∴,
设点A的坐标为,
∴,,
∴,
∴(负值舍去),
∴,,
把,代入得,
∴;
②延长交y轴于P,
∵,,
∴点B与点D关于y轴对称,
∴,
则点P即为符合条件的点,
由①知,,,
∴,,
设直线的解析式为,
∴,
∴,
∴直线的解析式为,
当时,,
∴.
故当最大时,点P的坐标为.
【解析】【分析】本题考查反比例函数、正方形的性质、轴对称的性质等知识点,
(1)根据轴对称的性质,设点A的坐标为,可以得出,平分,然后作图连接交于H,求出点,即可说明点E在这个反比例函数的图象上;
(2)①根据正方形的性质得出,垂直平分,设出点A的坐标为,求出点A、点C的坐标代入,即可求出k、b的值;
②作图,延长交y轴于P,得出点B与点D关于y轴对称,则点P即为符合条件的点,再根据①中求出的A、C坐标可求出a、n的值,从而得到直线的解析式即可求解.
21.【答案】(1)解:①设药物燃烧时的函数解析式为,药物燃烧后的解析式为,
把代入中得:,
∴,
∴药物燃烧时的函数解析式为,
∴药物刚好燃烧完时教室内每立方米空气含药量为,
把代入中得:,
∴,
∴药物燃烧后的解析式为;
②在中,当时,,
∵,
∴当时,y随x增大而增大,
∴当时,学生不能在教室停留;
在中,当时,,
∵,
∴当时,y随x增大而减小,
∴当时,学生不能在教室停留;
综上所述,当时,学生不能在教室停留;
(2)解:设要一次性燃烧完这种药物需t分钟,
同理可得当时,,
当药物刚好燃烧完时教室内每立方米空气含药量为,
同理可得时,,
在中,当时,,
∴当时为有效消毒时间;
在中,当时,,
∴当时为有效消毒时间;
综上所述,当时为有效消毒时间,
∵有效消毒时间为120分钟,
∴,
解得(负值舍去),
∴要一次性燃烧完这种药物需11分钟.
【解析】【分析】(1) ① 先利用待定系数法求出药物燃烧时的函数解析式为,进而求出药物刚好燃烧完时教室内每立方米空气含药量为7mg,从而即可利用待定系数法求出药物燃烧后的解析式;② 分别求出药物燃烧时和药物燃烧后,时x的值即可得到答案;
(2)设要一次性燃烧完这种药物需t分钟,仿照(1)①求出对应时间段的函数解析式,进而求出当y=0.7时x的值,再根据有效消毒时间为120分钟建立方程求解即可.
22.【答案】(1)平行四边形
(2)解:把A(n,3) 代入 y= 中,得3n=3,
∴n=1,
∴A(1,3),
∴OA=,
∵ 四边形ABCD是矩形 ,
∴OB=OA=,
∴m=;
(3)不能,理由如下:
∵点A在第一象限,B在x轴上,
∴∠AOB<90°,即得AC与BD不可能垂直,
∴ 四边形ABCD不能成为菱形 ;
【解析】【解答】解:(1)∵ 正比例函数y=kx(k>0)与反比例函数y=的图象分别交于A、C两点,
∴点A、C关于原点对称,即OA=OC,
∵点B与点D关于坐标原点O成中心对称 ,
∴OB=OD,
∴ 四边形ABCD是平行四边形;
故答案为:平行四边形.
【分析】(1)根据正比例函数与反比例函数的对称性可知OA=OC,结合题意知OB=OD,根据对角线互相平分可证四边形ABCD是平行四边形;
(2)将A(n,3) 代入 y= 中求出n值,即得A(1,3),利用勾股定理求出OA的长,根据矩形的性质可得OB=OA,据此即得m值;
(3)由点A在第一象限,B在x轴上,可知∠AOB<90°,即得AC与BD不可能垂直,根据菱形的性质即可判断.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
