浙教版九年级数学上册第3章圆的基本性质单元复习题(含解析)
文档属性
| 名称 | 浙教版九年级数学上册第3章圆的基本性质单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览



文档简介
浙教版九年级数学上册第3章圆的基本性质单元复习题
一、选择题
1.已知⊙O的半径为4cm,点P到圆心O的距离为3cm,则点P( )
A.在圆内 B.在圆上 C.在圆外 D.不能确定
2. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( )
A.144 B.120 C.72 D.60
3. 如图,⊙O的半径为10,弦长AB=16,弦心距OC的长为( )
A.5 B.6 C.7 D.8
4.如图,在中,若,则的度数是( )
A.15° B.25° C.50° D.75°
5.如图,A、B、C是⊙O上的三个点,若∠B=30°,则∠OAC的度数为( )
A.15° B.30° C.50° D.60°
6.在平面直角坐标系中,以原点为圆心,为半径作圆,点的坐标是,则点与的位置关系是( )
A.点在内 B.点在外
C.点在上 D.点在上或在外
7.如图,已知的半径为是直径,是弦,是的中点,连接分别与交于点,若点是的中点,则的长是( )
A.7 B.6 C.4 D.3
8.如图,四边形是的内接四边形,是的直径,.若.则的大小为( )
A. B. C. D.
9.一个扇形的半径是,扇形的圆心角,那么这个扇形面积是( )
A. B. C. D.
10.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是( )
A.36° B.45° C.48° D.60°
二、填空题
11. 如图,将Rt△ABC绕点A逆时针旋转50°得到Rt△AB1C1,∠C=90°,若∠BAC1=20°,则∠B= 度.
12.如图,在中,直径,弦相交于点.连接.且,若,则的度数为 .
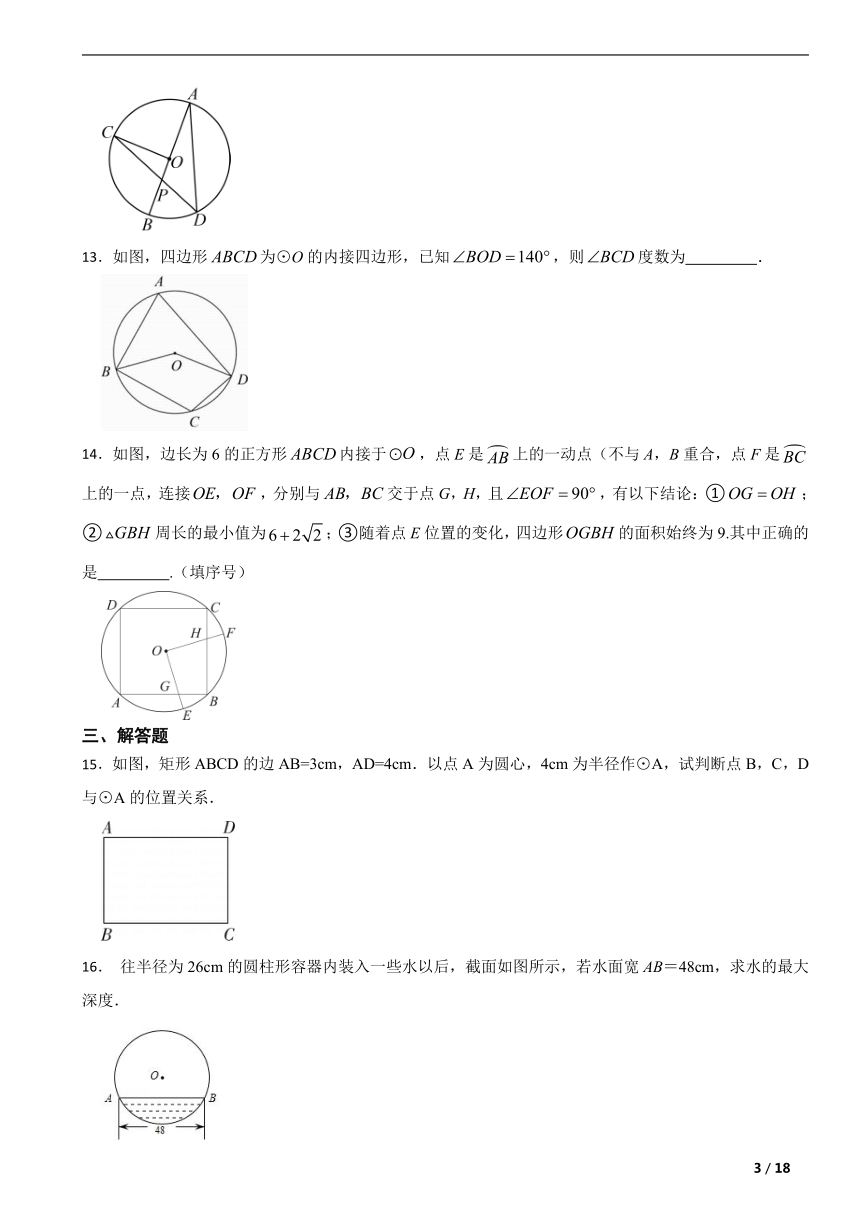
13.如图,四边形为⊙O的内接四边形,已知,则度数为 .
14.如图,边长为6的正方形内接于,点E是上的一动点(不与A,B重合,点F是上的一点,连接,分别与交于点G,H,且,有以下结论:①;②周长的最小值为;③随着点E位置的变化,四边形的面积始终为9.其中正确的是 .(填序号)
三、解答题
15.如图,矩形ABCD的边AB=3cm,AD=4cm.以点A为圆心,4cm为半径作⊙A,试判断点B,C,D与⊙A的位置关系.
16. 往半径为26cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,求水的最大深度.
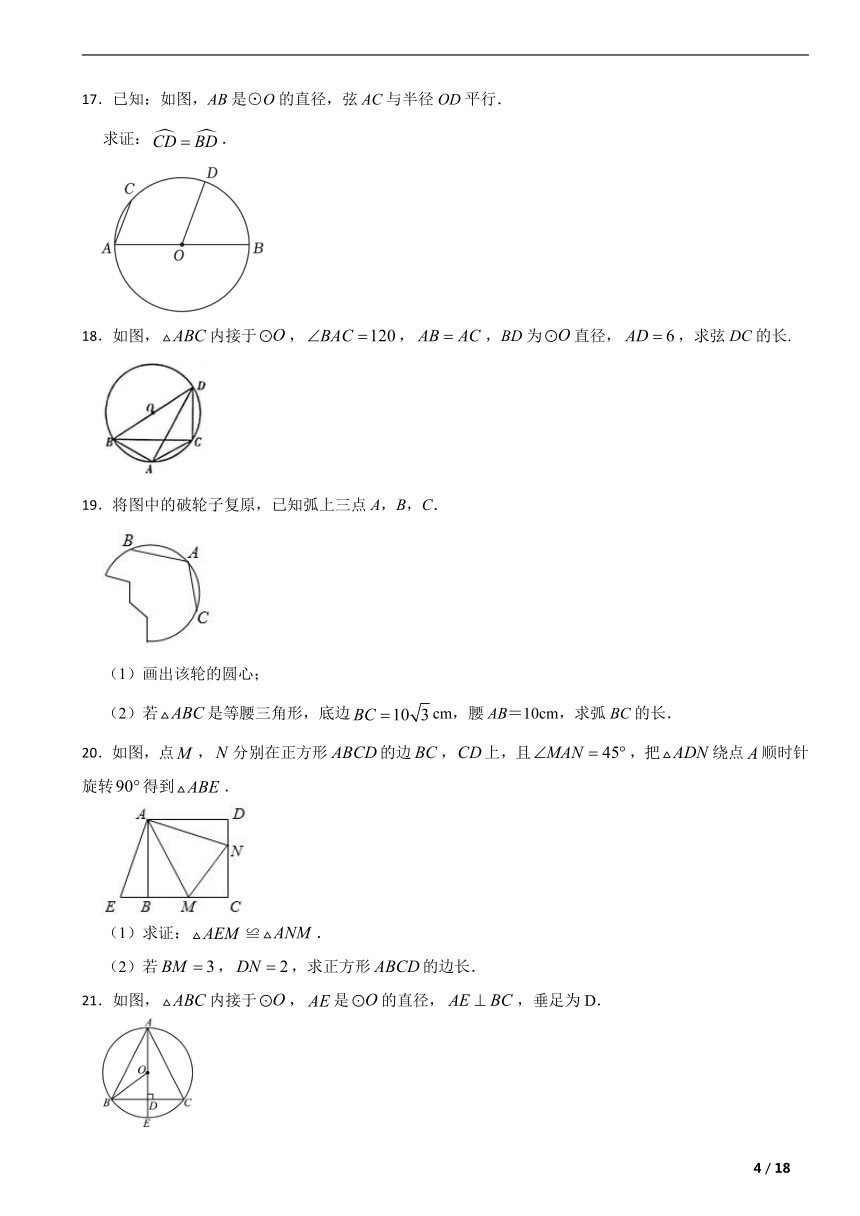
17.已知:如图,AB是⊙O的直径,弦AC与半径OD平行.
求证:.
18.如图,内接于,,,BD为直径,,求弦DC的长.
19.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若是等腰三角形,底边cm,腰AB=10cm,求弧BC的长.
20.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
21.如图,内接于,是的直径,,垂足为D.
(1)求证:;
(2)已知的半径为5,,求长.
22.如图,六边形ABCDEF是的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分.
(2)设的面积为,六边形ABCDEF的面积为,求的值.
23.如图,点P是等边三角形中边上的动点(),作的外接圆交于点D.点E是圆上一点,且,连接交于点F.
(1)求证:
(2)当点P运动变化时,的度数是否发生变化?若变化,请说明理由;若不变,求的度数.
(3)探究线段、、之间的数量关系,并证明.
答案解析部分
1.【答案】A
【解析】【解答】点到圆心的距离为3,小于圆的半径5,所以点在圆内,故答案为A。
【分析】考查点与圆的位置关系:比较点到圆心的距离与半径的大小,当点到圆心的距离大于半径,点在圆外;当点到圆心的距离等于半径,点在圆上;点到圆心的距离小于半径,点在圆内。
2.【答案】C
【解析】【解答】解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,
旋转的度数至少为,
故答案为:C
【分析】根据旋转的性质结合五角星的度数即可求解。
3.【答案】B
【解析】【解答】解: 弦心距.
故答案为:B.
【分析】根据垂径定理和勾股定理,代入求解.
4.【答案】C
【解析】【解答】解:由题意可得:
故答案为:C
【分析】根据同弧所对的圆周角是圆心角的一半即可求出答案.
5.【答案】D
6.【答案】C
【解析】【解答】解:∵圆心O的坐标为,点P的坐标为,
∴,因而点P在上.
故答案为:B
【分析】先根据勾股定理求出OP,进而根据点与圆的位置关系即可求解。
7.【答案】B
【解析】【解答】解:连接,
∵是的中点,连接,
∴垂直平分,
∵点O和F分别是、的中点,
∴,,
∴,
∵点是的中点,
∴,
又∵,
∴,
∴,
∴,
∵⊙O的半径为,
∴,
∴,
故答案为:B
【分析】根据垂径定理、三角形中位线定理、全等三角形的判定和性质求解。连接,由垂径定理证明垂直平分,由点O和F分别是、的中点得到,,再证明,得到,则,由即可得到的长.
8.【答案】D
【解析】【解答】连接BD,如图所示:
∵四边形ABCD是的内接四边形,∠A=50°,
∴∠C=180°-∠A=180°-50°=130°,
∵,
∴CD=CB,
∴∠CDB=∠CBD,
在△CDB中,∠CBD=,
∵AB是的直径,
∴∠ADB=90°,
在△ABD中,∠ABD=180°-∠ADB-∠A=40°,
∴∠ABC=∠ABD+∠CBD=40°+25°=65°,
故答案为:D.
【分析】利用圆内接四边形的性质求出∠C的度数,再利用弧与弦的关系和三角形的内角和求出∠CBD=,再利用圆周角和三角形内角和的性质求出∠ABD=180°-∠ADB-∠A=40°,最后利用角的运算求出∠ABC的度数即可.
9.【答案】B
【解析】【解答】解: 这个扇形面积为=3π.
故答案为:B.
【分析】扇形面积公式为据此计算即可.
10.【答案】C
【解析】【解答】 解:连接AO
∵△AMN是等边三角形
∴∠ANM=60°
∴∠AOM=2∠ANM=120°
∵ABCDE是正五边形
∴
∴
故答案为:C
【分析】连接AO,根据等边三角形性质及三角形内角和定理可得∠ANM=60°,根据圆周角定理可得∠AOM=2∠ANM=120°,根据正多边形内角和定理可得∠AOB=72°,则∠BOM=∠AOM-∠AOB即可求出答案.
11.【答案】60
【解析】【解答】因为Rt△ABC绕点A逆时针旋转50°得到Rt△AB1C1,∠BAC1=20°,所以∠CAC1=50°,∠CAB=50°-20°=30°,所以∠B=180°-90°-30°=60°.
故答案为:60.
【分析】根据题意可以求出∠CAB,再根据三角形内角为180°求出∠B的度数。
12.【答案】
【解析】【解答】解:∵AB为⊙O的直径,OC⊥AB,
∴∠AOC=90°,
∴∠ADC=∠AOC=×90°=45°,
∵∠A=20°,
∴∠BPD=∠A+∠ADC=20°+45°=65°.
故答案为:65°.
【分析】由垂直定义得∠AOC=90°,根据圆周角定理可得∠ADC=∠AOC,然后根据三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”可求解.
13.【答案】110°
14.【答案】①③
【解析】【解答】解:如图,连接 .
∵ ,
∴ .
∵四边形 为正方形,
∴ , , ,
∴ ,
∴ ,
∴ ,
∴ ,故①正确;
∵ ,
∴ ,
∴ ,
∴ 的周长为 ,
∴当 最小时, 周长的最小.
∵ ,
∴当 最小时, 最小,此时 .
如图,过点O作 于点M,作 于点N,
∴ ,
∴ ,
∴ 的周长的最小值为 ,故②错误;
∵ ,
∴ .
∴ .
∵ ,
∴ ,故③正确.
综上可知①③正确.
故答案为:①③.
【分析】连接OC、OB,根据正方形的性质可得∠BOC=90°,OB=OC,∠OBG=∠OCH=45°,由同角的余角相等可得∠BOG=∠COH,利用ASA证明△BOG≌△COH,据此判断①;根据全等三角形的性质可得BG=CH,则BH+BG=BH+CH=BC=6,△GBH的周长为6+HG,由勾股定理可得HG=,故当OH、OG最小时,HG最小,此时OH⊥BC,OG⊥AB,过点O作OM⊥BC于点M,作ON⊥AB于点N,则OM=PN=3,利用勾股定理可得HG,据此判断②;根据全等三角形的性质可得S△BOG=S△COH,推出S△BOC=S正方形ABCD,据此判断③.
15.【答案】解:连接AC,如图:
∵AB=3cm,AD=4cm,
∴cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
【解析】【分析】先根据直角三角形中两直角边的平方和等于斜边的平方求出AC的长,根据点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r;进行分析即可求解.
16.【答案】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48,
∴BD=AB=×48=24,
∵⊙O的直径为52,
∴OB=OC=26,
在Rt△OBD中,OD===10,
∴CD=OC﹣OD=26﹣10=16(cm).
【解析】【分析】 连接OB,过点O作OC⊥AB于点D,交⊙O于点C, 由垂径定理可得BD=AB=24, 在Rt△OBD中,由勾股定理求出OD=10, 利用CD=OC﹣OD即可求解.
17.【答案】证明:连接OC,
∵OC=OA,
∴∠A=∠C,
∵AC∥OD,
∴∠COD=∠C,∠BOD=∠A,
∴∠COD=∠BOD,
∴.
【解析】【分析】 连接OC, 可得出 ∠A=∠C, 然后根据平行线的性质分别得出 ∠COD=∠C,∠BOD=∠A, 即可得到 ∠COD=∠BOD, 进而得出 .
18.【答案】解:为的直径,
,
,
.
,
又,.
.
.
在中,,
,
在中,.
【解析】【分析】利用直径所对的圆周角是直角得出∠BAD=∠BCD=90°,结合∠BAC=120°求出∠CAD=30°,由同弧所对的圆周角相等,求出∠CBD=∠CAD=30°;利用圆内接四边形对角互补,求出∠BDC=60°;利用AB=AC求出∠ADB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求解即可.
19.【答案】(1)解:如图,点O即为圆心;
(2)解:连接AO,OB,OC,BC,BC交OA于D.
∵△ABC是等腰三角形,
∴AB=AC=10cm,
∵BC=cm,
∴BD=cm,
∴AD==5cm,
设圆片的半径为R,在Rt△BOD中,OD=(R-5)cm,
∴,
解得:R=10,
∴△OAB和△OAC为等边三角形,
∴∠BOC为120°,
∴弧BC的长为:=cm.
【解析】【分析】(1)利用垂径定理,分别作弦AB、AC的垂直平分线,其交点即为所求;
(2) 连接AO,OB,OC,BC,BC交OA于D,利用等腰三角形的性质以及勾股定理判断△OAB和△OAC为等边三角形, 求得 ∠BOC为120°, 利用弧长公式代入数据计算即可求解;
20.【答案】(1)解:由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)解:设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
【解析】【分析】(1)利用“SAS”证明即可;
(2)设正方形的边长为x,则,根据全等三角形的性质可得,再利用勾股定理可得,最后求出x的值即可。
21.【答案】(1)证明:∵是的直径,,
∴,
∴,
∵,
∴是等腰三角形,
∴,
∴;
(2)解:∵是的直径,,
∴,,
在中,,,
∴,
∴.
【解析】【分析】(1)根据垂径定理可得,再根据 是等腰三角形,可得,即可得到;
(2)先求出,OB=5,利用勾股定理求出BD的长,再求出即可。
22.【答案】(1)解:连接AE,AD,AC,
∵六边形ABCDEF是的内接正六边形,
∴EF=ED=CD=BC,
∴∠FAE=∠EAD=∠DAC=∠CAB,
即过顶点A的三条对角线四等分;
(2)解:过点O作OG⊥DE于G,连接OE,
设圆O的半径为r,
∴EF=BC=ED=r,AD=2r,
在正六边形ABCDEF中,
∠OED=∠ODE=60°,
∴∠EOG=30°,
∴EG=r,
∴OG==r,
∴正六边形ABCDEF的面积==,
圆O的面积=,
∴==.
【解析】【分析】(1)连接AE,AD,AC,由正多边形的性质得EF=ED=CD=BC,再利用同圆中弧、弦、圆心角之间的关系及圆周角定理得∠FAE=∠EAD=∠DAC=∠CAB,由此可证得结论;
(2)过点O作OG⊥DE于G,连接OE,设圆O的半径为r,可得EF=BC=ED=r,AD=2r,由正六边形的性质可求出∠EOG=30°,利用30°角所对的直角边等于斜边的一半可证得 EG=r, 利用勾股定理表示出OG的长,然后求出正六边形的面积和圆O的面积,然后求出 的值 .
23.【答案】(1)证明:连接PE,
∵△ABC是等边三角形,
∴AB=BC,∠A=∠ACB=60°,
∴∠PEB=∠ACB=60°,
∴∠A=∠PEB,
∵ ,
∴∠PBD=∠PBE,
∵BP=BP,
∴△ABP≌△EBP(AAS),
∴AB=EB,
∴EB=BC;
(2)解:当点P运动时,∠BFD的度数不会变化,
∵ ,
∴∠DEP=∠EBP,
∵∠BFD=∠EBP+∠DEB,
∴∠BFD=∠DEP+∠DEB
=∠PEB
=60°,
∴∠BFD的度数为60°;
(3)解: ,理由如下:
延长 交于点J,
,
,
,
是等边三角形,
,
在 和 中,
, ,
,
连接 ,
四边形 是圆的内接四边形,
,
,
,
,
是等边三角形,
,
,即 ,
在 和 中,
,
,
,
,
即 .
【解析】【分析】(1)连接PE,由等边三角形的性质可得AB=BC,∠A=∠ACB=60°,由圆周角定理可得∠PEB=∠ACB=60°,∠PBD=∠PBE,利用AAS证明△ABP≌△EBP,得到AB=EB,据此证明;
(2)由圆周角定理可得∠DEP=∠EBP,由外角的性质可得∠BFD=∠EBP+∠DEB,则∠BFD=∠DEP+∠DEB=∠PEB,据此解答;
(3)延长CE、BP交于点J,由圆内接四边形的性质可得∠ABC+∠CED=180°,结合邻补角的性质可得∠JEF=∠ABC=60°,推出△JEF是等边三角形,EF=JE,根据对顶角的性质结合内角和定理可得∠JCP=∠PBA,连接PD,由圆内接四边形的性质可得∠PCB+∠PDB=180°,结合邻补角的性质可得∠ADP=∠PCB=60°,推出△ADP是等边三角形,的搭配AD=AP,结合线段的和差关系可得PC=DB,利用AAS证明△JPC≌△FDB,得到BF=JC,据此证明.
1 / 1
一、选择题
1.已知⊙O的半径为4cm,点P到圆心O的距离为3cm,则点P( )
A.在圆内 B.在圆上 C.在圆外 D.不能确定
2. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( )
A.144 B.120 C.72 D.60
3. 如图,⊙O的半径为10,弦长AB=16,弦心距OC的长为( )
A.5 B.6 C.7 D.8
4.如图,在中,若,则的度数是( )
A.15° B.25° C.50° D.75°
5.如图,A、B、C是⊙O上的三个点,若∠B=30°,则∠OAC的度数为( )
A.15° B.30° C.50° D.60°
6.在平面直角坐标系中,以原点为圆心,为半径作圆,点的坐标是,则点与的位置关系是( )
A.点在内 B.点在外
C.点在上 D.点在上或在外
7.如图,已知的半径为是直径,是弦,是的中点,连接分别与交于点,若点是的中点,则的长是( )
A.7 B.6 C.4 D.3
8.如图,四边形是的内接四边形,是的直径,.若.则的大小为( )
A. B. C. D.
9.一个扇形的半径是,扇形的圆心角,那么这个扇形面积是( )
A. B. C. D.
10.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是( )
A.36° B.45° C.48° D.60°
二、填空题
11. 如图,将Rt△ABC绕点A逆时针旋转50°得到Rt△AB1C1,∠C=90°,若∠BAC1=20°,则∠B= 度.
12.如图,在中,直径,弦相交于点.连接.且,若,则的度数为 .
13.如图,四边形为⊙O的内接四边形,已知,则度数为 .
14.如图,边长为6的正方形内接于,点E是上的一动点(不与A,B重合,点F是上的一点,连接,分别与交于点G,H,且,有以下结论:①;②周长的最小值为;③随着点E位置的变化,四边形的面积始终为9.其中正确的是 .(填序号)
三、解答题
15.如图,矩形ABCD的边AB=3cm,AD=4cm.以点A为圆心,4cm为半径作⊙A,试判断点B,C,D与⊙A的位置关系.
16. 往半径为26cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,求水的最大深度.
17.已知:如图,AB是⊙O的直径,弦AC与半径OD平行.
求证:.
18.如图,内接于,,,BD为直径,,求弦DC的长.
19.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若是等腰三角形,底边cm,腰AB=10cm,求弧BC的长.
20.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
21.如图,内接于,是的直径,,垂足为D.
(1)求证:;
(2)已知的半径为5,,求长.
22.如图,六边形ABCDEF是的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分.
(2)设的面积为,六边形ABCDEF的面积为,求的值.
23.如图,点P是等边三角形中边上的动点(),作的外接圆交于点D.点E是圆上一点,且,连接交于点F.
(1)求证:
(2)当点P运动变化时,的度数是否发生变化?若变化,请说明理由;若不变,求的度数.
(3)探究线段、、之间的数量关系,并证明.
答案解析部分
1.【答案】A
【解析】【解答】点到圆心的距离为3,小于圆的半径5,所以点在圆内,故答案为A。
【分析】考查点与圆的位置关系:比较点到圆心的距离与半径的大小,当点到圆心的距离大于半径,点在圆外;当点到圆心的距离等于半径,点在圆上;点到圆心的距离小于半径,点在圆内。
2.【答案】C
【解析】【解答】解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,
旋转的度数至少为,
故答案为:C
【分析】根据旋转的性质结合五角星的度数即可求解。
3.【答案】B
【解析】【解答】解: 弦心距.
故答案为:B.
【分析】根据垂径定理和勾股定理,代入求解.
4.【答案】C
【解析】【解答】解:由题意可得:
故答案为:C
【分析】根据同弧所对的圆周角是圆心角的一半即可求出答案.
5.【答案】D
6.【答案】C
【解析】【解答】解:∵圆心O的坐标为,点P的坐标为,
∴,因而点P在上.
故答案为:B
【分析】先根据勾股定理求出OP,进而根据点与圆的位置关系即可求解。
7.【答案】B
【解析】【解答】解:连接,
∵是的中点,连接,
∴垂直平分,
∵点O和F分别是、的中点,
∴,,
∴,
∵点是的中点,
∴,
又∵,
∴,
∴,
∴,
∵⊙O的半径为,
∴,
∴,
故答案为:B
【分析】根据垂径定理、三角形中位线定理、全等三角形的判定和性质求解。连接,由垂径定理证明垂直平分,由点O和F分别是、的中点得到,,再证明,得到,则,由即可得到的长.
8.【答案】D
【解析】【解答】连接BD,如图所示:
∵四边形ABCD是的内接四边形,∠A=50°,
∴∠C=180°-∠A=180°-50°=130°,
∵,
∴CD=CB,
∴∠CDB=∠CBD,
在△CDB中,∠CBD=,
∵AB是的直径,
∴∠ADB=90°,
在△ABD中,∠ABD=180°-∠ADB-∠A=40°,
∴∠ABC=∠ABD+∠CBD=40°+25°=65°,
故答案为:D.
【分析】利用圆内接四边形的性质求出∠C的度数,再利用弧与弦的关系和三角形的内角和求出∠CBD=,再利用圆周角和三角形内角和的性质求出∠ABD=180°-∠ADB-∠A=40°,最后利用角的运算求出∠ABC的度数即可.
9.【答案】B
【解析】【解答】解: 这个扇形面积为=3π.
故答案为:B.
【分析】扇形面积公式为据此计算即可.
10.【答案】C
【解析】【解答】 解:连接AO
∵△AMN是等边三角形
∴∠ANM=60°
∴∠AOM=2∠ANM=120°
∵ABCDE是正五边形
∴
∴
故答案为:C
【分析】连接AO,根据等边三角形性质及三角形内角和定理可得∠ANM=60°,根据圆周角定理可得∠AOM=2∠ANM=120°,根据正多边形内角和定理可得∠AOB=72°,则∠BOM=∠AOM-∠AOB即可求出答案.
11.【答案】60
【解析】【解答】因为Rt△ABC绕点A逆时针旋转50°得到Rt△AB1C1,∠BAC1=20°,所以∠CAC1=50°,∠CAB=50°-20°=30°,所以∠B=180°-90°-30°=60°.
故答案为:60.
【分析】根据题意可以求出∠CAB,再根据三角形内角为180°求出∠B的度数。
12.【答案】
【解析】【解答】解:∵AB为⊙O的直径,OC⊥AB,
∴∠AOC=90°,
∴∠ADC=∠AOC=×90°=45°,
∵∠A=20°,
∴∠BPD=∠A+∠ADC=20°+45°=65°.
故答案为:65°.
【分析】由垂直定义得∠AOC=90°,根据圆周角定理可得∠ADC=∠AOC,然后根据三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”可求解.
13.【答案】110°
14.【答案】①③
【解析】【解答】解:如图,连接 .
∵ ,
∴ .
∵四边形 为正方形,
∴ , , ,
∴ ,
∴ ,
∴ ,
∴ ,故①正确;
∵ ,
∴ ,
∴ ,
∴ 的周长为 ,
∴当 最小时, 周长的最小.
∵ ,
∴当 最小时, 最小,此时 .
如图,过点O作 于点M,作 于点N,
∴ ,
∴ ,
∴ 的周长的最小值为 ,故②错误;
∵ ,
∴ .
∴ .
∵ ,
∴ ,故③正确.
综上可知①③正确.
故答案为:①③.
【分析】连接OC、OB,根据正方形的性质可得∠BOC=90°,OB=OC,∠OBG=∠OCH=45°,由同角的余角相等可得∠BOG=∠COH,利用ASA证明△BOG≌△COH,据此判断①;根据全等三角形的性质可得BG=CH,则BH+BG=BH+CH=BC=6,△GBH的周长为6+HG,由勾股定理可得HG=,故当OH、OG最小时,HG最小,此时OH⊥BC,OG⊥AB,过点O作OM⊥BC于点M,作ON⊥AB于点N,则OM=PN=3,利用勾股定理可得HG,据此判断②;根据全等三角形的性质可得S△BOG=S△COH,推出S△BOC=S正方形ABCD,据此判断③.
15.【答案】解:连接AC,如图:
∵AB=3cm,AD=4cm,
∴cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
【解析】【分析】先根据直角三角形中两直角边的平方和等于斜边的平方求出AC的长,根据点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r;进行分析即可求解.
16.【答案】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48,
∴BD=AB=×48=24,
∵⊙O的直径为52,
∴OB=OC=26,
在Rt△OBD中,OD===10,
∴CD=OC﹣OD=26﹣10=16(cm).
【解析】【分析】 连接OB,过点O作OC⊥AB于点D,交⊙O于点C, 由垂径定理可得BD=AB=24, 在Rt△OBD中,由勾股定理求出OD=10, 利用CD=OC﹣OD即可求解.
17.【答案】证明:连接OC,
∵OC=OA,
∴∠A=∠C,
∵AC∥OD,
∴∠COD=∠C,∠BOD=∠A,
∴∠COD=∠BOD,
∴.
【解析】【分析】 连接OC, 可得出 ∠A=∠C, 然后根据平行线的性质分别得出 ∠COD=∠C,∠BOD=∠A, 即可得到 ∠COD=∠BOD, 进而得出 .
18.【答案】解:为的直径,
,
,
.
,
又,.
.
.
在中,,
,
在中,.
【解析】【分析】利用直径所对的圆周角是直角得出∠BAD=∠BCD=90°,结合∠BAC=120°求出∠CAD=30°,由同弧所对的圆周角相等,求出∠CBD=∠CAD=30°;利用圆内接四边形对角互补,求出∠BDC=60°;利用AB=AC求出∠ADB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求解即可.
19.【答案】(1)解:如图,点O即为圆心;
(2)解:连接AO,OB,OC,BC,BC交OA于D.
∵△ABC是等腰三角形,
∴AB=AC=10cm,
∵BC=cm,
∴BD=cm,
∴AD==5cm,
设圆片的半径为R,在Rt△BOD中,OD=(R-5)cm,
∴,
解得:R=10,
∴△OAB和△OAC为等边三角形,
∴∠BOC为120°,
∴弧BC的长为:=cm.
【解析】【分析】(1)利用垂径定理,分别作弦AB、AC的垂直平分线,其交点即为所求;
(2) 连接AO,OB,OC,BC,BC交OA于D,利用等腰三角形的性质以及勾股定理判断△OAB和△OAC为等边三角形, 求得 ∠BOC为120°, 利用弧长公式代入数据计算即可求解;
20.【答案】(1)解:由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)解:设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
【解析】【分析】(1)利用“SAS”证明即可;
(2)设正方形的边长为x,则,根据全等三角形的性质可得,再利用勾股定理可得,最后求出x的值即可。
21.【答案】(1)证明:∵是的直径,,
∴,
∴,
∵,
∴是等腰三角形,
∴,
∴;
(2)解:∵是的直径,,
∴,,
在中,,,
∴,
∴.
【解析】【分析】(1)根据垂径定理可得,再根据 是等腰三角形,可得,即可得到;
(2)先求出,OB=5,利用勾股定理求出BD的长,再求出即可。
22.【答案】(1)解:连接AE,AD,AC,
∵六边形ABCDEF是的内接正六边形,
∴EF=ED=CD=BC,
∴∠FAE=∠EAD=∠DAC=∠CAB,
即过顶点A的三条对角线四等分;
(2)解:过点O作OG⊥DE于G,连接OE,
设圆O的半径为r,
∴EF=BC=ED=r,AD=2r,
在正六边形ABCDEF中,
∠OED=∠ODE=60°,
∴∠EOG=30°,
∴EG=r,
∴OG==r,
∴正六边形ABCDEF的面积==,
圆O的面积=,
∴==.
【解析】【分析】(1)连接AE,AD,AC,由正多边形的性质得EF=ED=CD=BC,再利用同圆中弧、弦、圆心角之间的关系及圆周角定理得∠FAE=∠EAD=∠DAC=∠CAB,由此可证得结论;
(2)过点O作OG⊥DE于G,连接OE,设圆O的半径为r,可得EF=BC=ED=r,AD=2r,由正六边形的性质可求出∠EOG=30°,利用30°角所对的直角边等于斜边的一半可证得 EG=r, 利用勾股定理表示出OG的长,然后求出正六边形的面积和圆O的面积,然后求出 的值 .
23.【答案】(1)证明:连接PE,
∵△ABC是等边三角形,
∴AB=BC,∠A=∠ACB=60°,
∴∠PEB=∠ACB=60°,
∴∠A=∠PEB,
∵ ,
∴∠PBD=∠PBE,
∵BP=BP,
∴△ABP≌△EBP(AAS),
∴AB=EB,
∴EB=BC;
(2)解:当点P运动时,∠BFD的度数不会变化,
∵ ,
∴∠DEP=∠EBP,
∵∠BFD=∠EBP+∠DEB,
∴∠BFD=∠DEP+∠DEB
=∠PEB
=60°,
∴∠BFD的度数为60°;
(3)解: ,理由如下:
延长 交于点J,
,
,
,
是等边三角形,
,
在 和 中,
, ,
,
连接 ,
四边形 是圆的内接四边形,
,
,
,
,
是等边三角形,
,
,即 ,
在 和 中,
,
,
,
,
即 .
【解析】【分析】(1)连接PE,由等边三角形的性质可得AB=BC,∠A=∠ACB=60°,由圆周角定理可得∠PEB=∠ACB=60°,∠PBD=∠PBE,利用AAS证明△ABP≌△EBP,得到AB=EB,据此证明;
(2)由圆周角定理可得∠DEP=∠EBP,由外角的性质可得∠BFD=∠EBP+∠DEB,则∠BFD=∠DEP+∠DEB=∠PEB,据此解答;
(3)延长CE、BP交于点J,由圆内接四边形的性质可得∠ABC+∠CED=180°,结合邻补角的性质可得∠JEF=∠ABC=60°,推出△JEF是等边三角形,EF=JE,根据对顶角的性质结合内角和定理可得∠JCP=∠PBA,连接PD,由圆内接四边形的性质可得∠PCB+∠PDB=180°,结合邻补角的性质可得∠ADP=∠PCB=60°,推出△ADP是等边三角形,的搭配AD=AP,结合线段的和差关系可得PC=DB,利用AAS证明△JPC≌△FDB,得到BF=JC,据此证明.
1 / 1
同课章节目录
